線路曲線點位測設數據計算軟件設計與開發
周命端,王 淼,張文堯,王賓賓,馬博泓
(1.北京建筑大學 測繪與城市空間信息學院,北京 102616;2.北京建筑大學 土木與交通工程學院,北京 102616;3.陜西鐵道工程勘察有限公司,陜西 西安 221116)
圓曲線是平面線形中常用的線性要素,公路或鐵路不論轉角大小均需設計圓曲線。交通載體從直線進入圓曲線時,駕駛員應逐漸改變轉向角,從直線過渡到圓曲線。交通載體在曲線行駛的曲率可能是不斷變化的,為適應這一曲率變化還需設置緩和曲線。另外,縱斷面設計中心線可由許多不同坡度的坡段構成豎曲線。無論是圓曲線、緩和曲線還是豎曲線,針對單一曲線的點位測設數據計算較為簡單。仝海飚以Visual C++6.0為開發平臺,設計開發了道路緩和曲線坐標法測設軟件[1];紀凱利用Excel的表格特性進行緩和曲線中樁坐標計算[2];張帥帥等人利用VB與Matlab設計實現緩和曲線坐標計算程序[3];郭有寶利用學生函數計算器快速計算緩和曲線測設數據[4-5]。然而,在實際線路設計中往往是多種類曲線復雜組合,現有工具軟件難以滿足這種組合的點位測設數據計算。本文基于VS2010開發平臺,利用C#編程語言,設計開發一種適用于多種類曲線組合的點位測設數據計算軟件(LPLS),并給出軟件設計與開發的程序實現流程圖,對提高線路曲線的點位測設數據計算工作效率具有重要的現實意義和實用價值。
1 點位測設數據計算模型
1.1 圓曲線坐標測設計算
圓曲線坐標測設計算原理[6-8]如圖1所示。假設M是圓曲線上任意點,其在施工坐標系下的坐標計算步驟為:
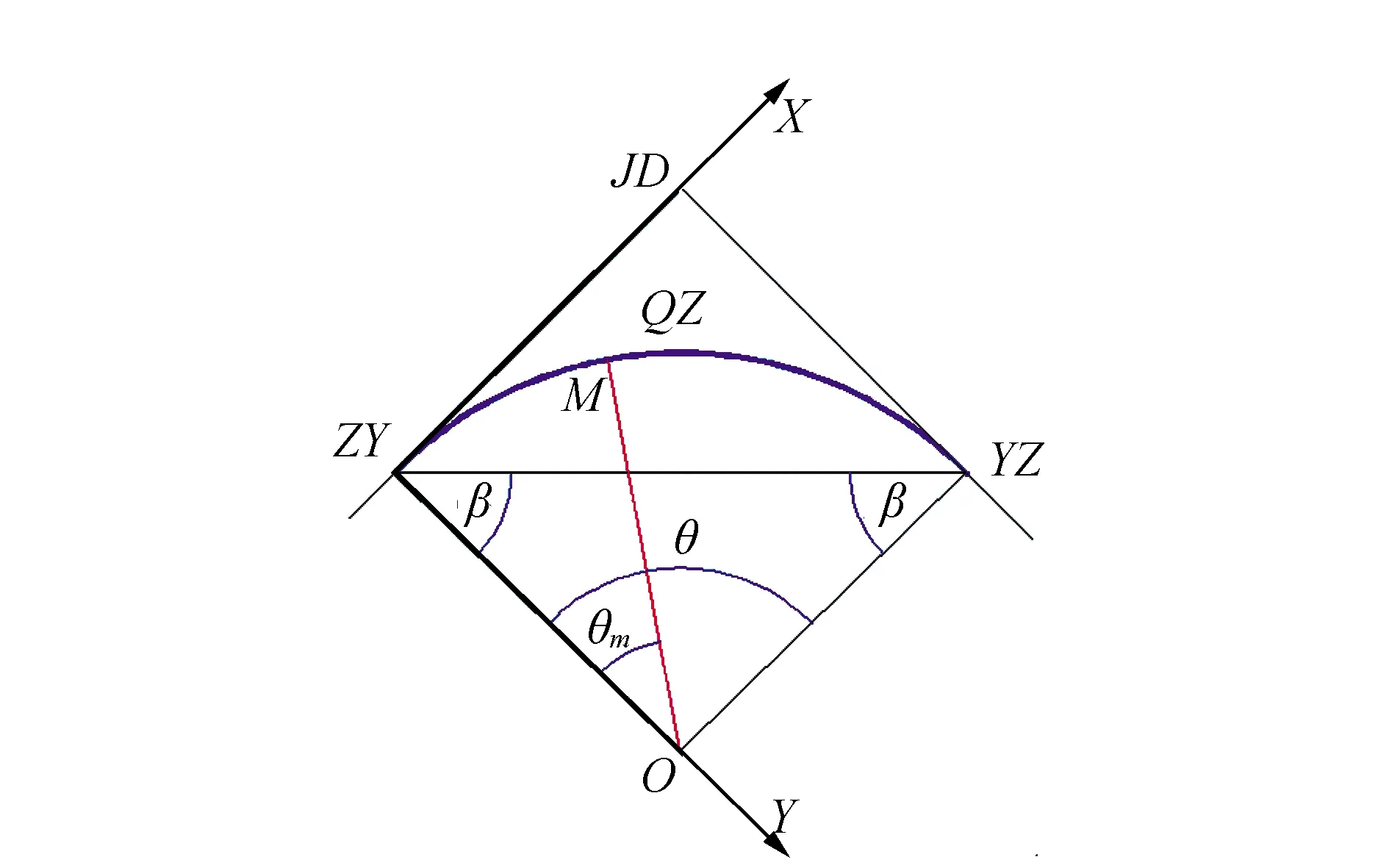
圖1 圓曲線坐標測設計算原理
1)計算圓心O的坐標。首先計算ZY點到YZ點的坐標方位角:
(1)
然后,計算ZY點到YZ點劣弧所對應的圓心角:
(2)
由式(2),可以求得β角:
(3)
根據式(1)和式(3),求得ZY點到O點的坐標方位角:
αZY→O=αZY→YZ+β.
(4)
根據坐標正算公式,計算圓心O的坐標:
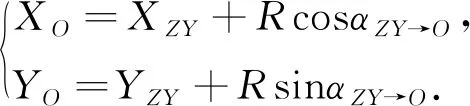
(5)
2)計算圓心O到ZY點的坐標方位角:
αO→ZY=αZY→O-180°.
(6)
3)計算圓心O到圓曲線上任意點M的坐標方位角。首先計算ZY點到M點的弧長lM:
lM=LM-LZY.
(7)
式中:LM為M點的里程;LZY為ZY點的里程。其次,計算ZY點到M點,劣弧所對應的圓心角:
(8)
根據式(6)和式(8),求得圓點O點到M點的坐標方位角:
αO→M=αO→ZY+θM.
(9)
4)計算M點的樁點坐標。根據式(9)以及坐標正算公式,計算M點的坐標:
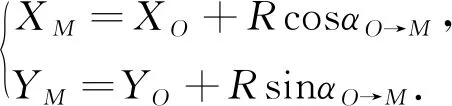
(10)
1.2 帶緩和曲線的圓曲線坐標測設計算
帶緩和曲線的圓曲線坐標測設計算原理[6-8]如圖2所示。
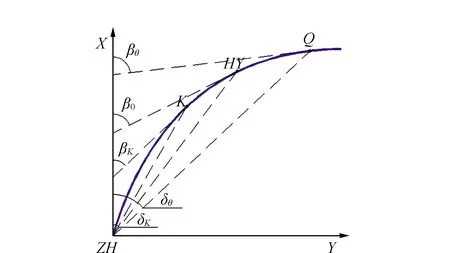
圖2 帶緩和曲線的圓曲線坐標測設計算原理
在圖2所示的獨立坐標系下,假如K是緩和曲線段上任意點,其在施工坐標系下的坐標計算步驟為:
1)計算K點的切線角βK和K點的偏角δK:
(11)
(12)
式中:LK是K點到ZH點的弧長,Lh是緩和曲線長度,R為圓曲線半徑。
2)計算K點到ZH點的偏角:
αK=αZH→JD+δK.
(13)
3)計算K點到ZH點的弦長Ck:
(14)
其中,K點坐標
4)計算K點在施工坐標系下的樁點坐標。根據式(13)和(14)以及坐標正算公式,計算K點在施工坐標系下的坐標:
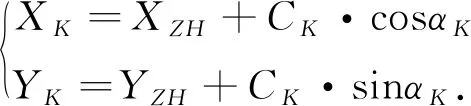
(15)
另一方面,在圖2所示的獨立坐標系下,若Q點是在帶緩和曲線的圓曲線上的任意點,其在施工坐標系下的坐標計算步驟為:
1)計算Q點的切線方位角:
(16)
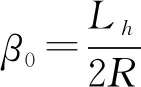
2)計算緩和曲線切線增值q和圓曲線的內移值ΔR:
(17)
(18)
3)由式(16)~(18)可得到獨立坐標系下Q點的坐標:
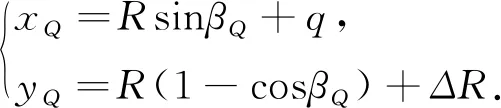
(19)
4)根據式(19)計算Q點到ZH點的偏角和Q點到ZH點的弧長:
αQ=αZH→JD+δQ,
(20)
(21)
5)根據式(20)、式(21)可計算得到施工坐標系下Q點的坐標:
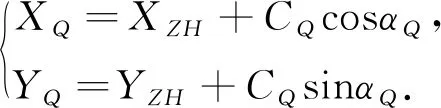
(22)
1.3 豎曲線高程測設計算
豎曲線高程測設計算原理[6-8]如圖3所示。假設V是豎曲線上任意點,其設計高程計算步驟為:
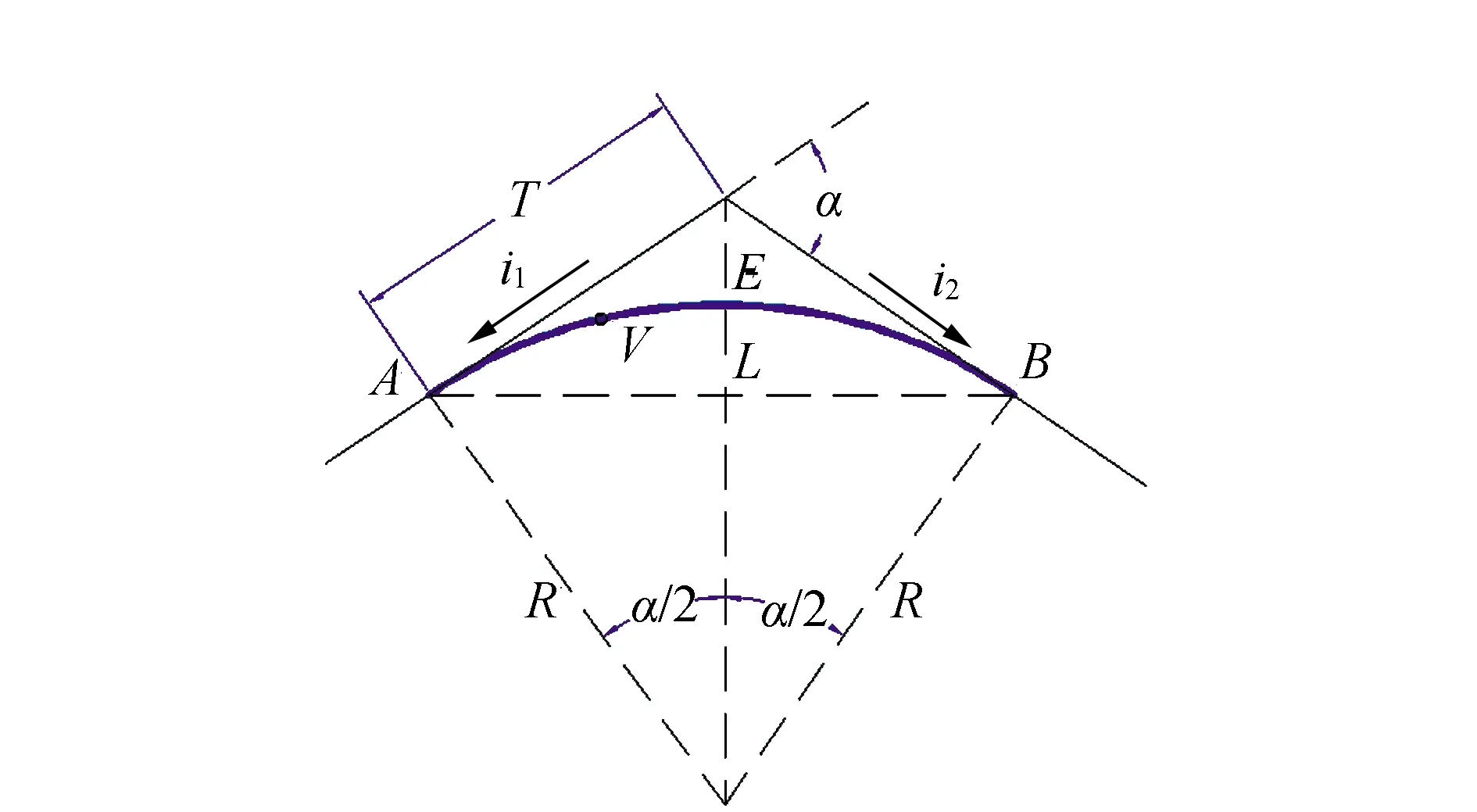
圖3 豎曲線高程測設計算原理
1)計算豎曲線的基本要素:曲折角α、豎曲線切線長T、豎曲線長度L和豎曲線外矢徑E,計算式所示:
(23)
2)計算起、終點的里程:
(24)
式中:MO為豎曲線起點里程;M變為變坡點里程;MD是豎曲線終點里程。
3)計算坡度線上任意點的切線高程:
(25)
dV=MV-MO,
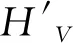
4)計算豎曲線各點與對應切線各點的高程之差h:
(26)
5)根據式(25)、式(26)計算豎曲線任意點V的設計高程:
(27)
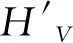
2 軟件設計與實現
根據推導的點位測設數據計算模型,包括圓曲線坐標測設計算、帶緩和曲線的圓曲線坐標測設計算和豎曲線高程測設計算,本文基于VS2010開發平臺,設計開發了線路曲線點位測設數據計算軟件(LPLS)。LPLS軟件主界面設計如圖4所示。
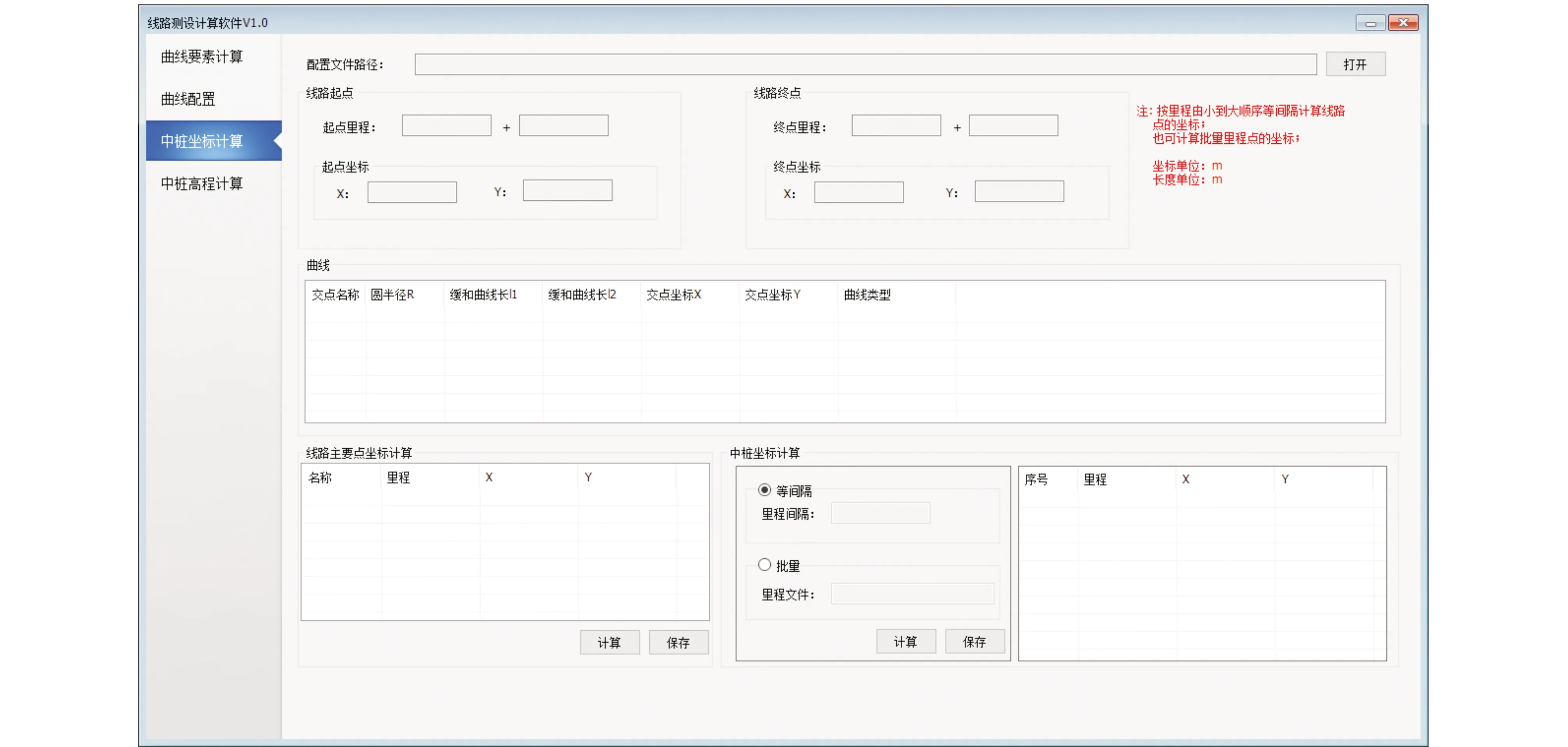
圖4 LPLS軟件主界面設計
利用C#編程語言,建立主要的程序模塊,包括曲線要素計算模塊、曲線配置模塊、中樁坐標計算模塊和中樁高程計算模塊。LPLS軟件主要程序模塊結構如圖5所示。
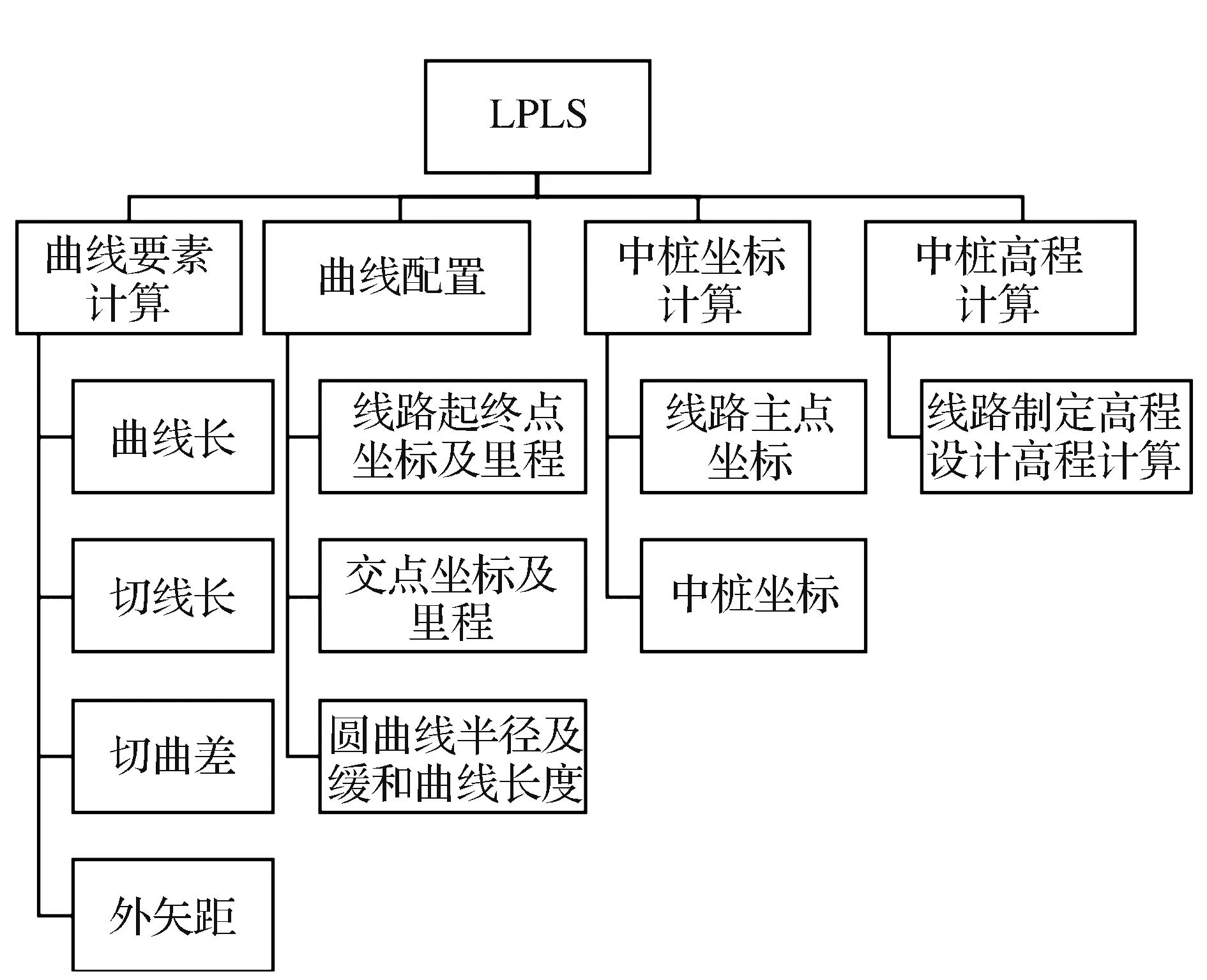
圖5 LPLS軟件主要程序模塊結構
如圖5所示,曲線要素計算模塊主要包括曲線長、切線長和切曲差的計算功能實現;曲線配置模塊主要由路線起、終坐標及里程、交點坐標及里程和圓曲線半徑及緩和曲線長度完成曲線配置;中樁坐標計算模塊是根據曲線要素計算模塊和曲線配置模塊實現線路主點坐標、線路中樁坐標的計算功能;豎曲線高程計算模塊可以實現線路中樁設計高程的計算功能。其中,中樁坐標計算程序模塊和中樁高程計算程序模塊是LPLS軟件的主要核心模塊,中樁坐標計算程序模塊實現流程圖如圖6所示,中樁高程計算程序模塊實現流程圖如圖7所示。
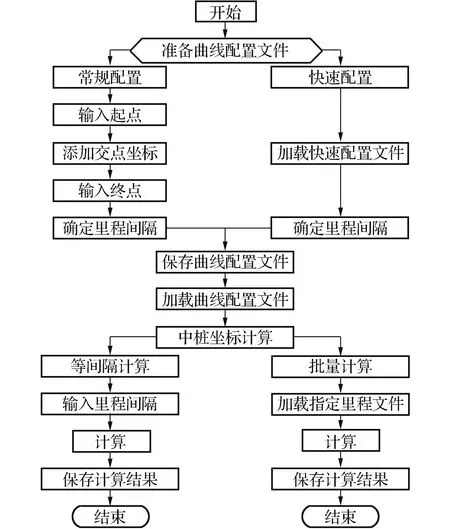
圖6 中樁坐標計算程序模塊實現流程
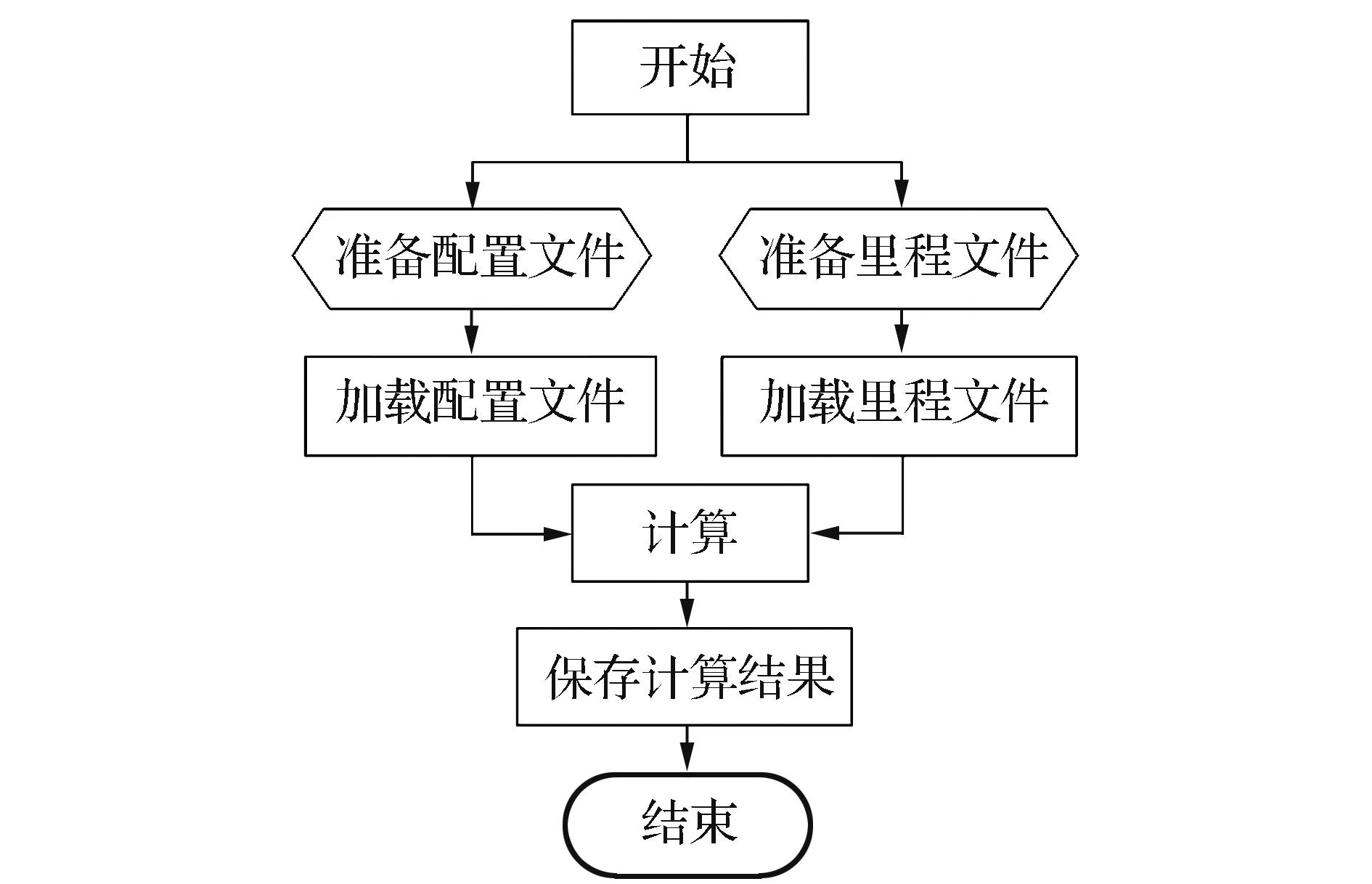
圖7 中樁高程計算程序模塊實現流程
3 算例驗證
為驗證與分析點位測設數據計算模型及程序功能模塊的正確性和有效性,本文選取鐵道工程的某工段里程的中樁點位測設數據進行算例驗證。
3.1 坐標計算
根據坐標計算式及計算步驟,基于VS2010開發平臺,利用C#編程語言,建立線路曲線平面坐標計算功能模塊(LPLS_H),基于LPLS軟件計算獲得DK6+813~DK9+430工段的每公里里程間隔的中樁平面坐標計算結果,如圖8所示。
圖8 中樁平面坐標計算結果
如圖8所示,為驗證LPLS軟件計算中樁平面坐標的正確性,本文截取包含緩和曲線、圓曲線等五段曲線段的隨機選取的里程點進行手工驗證計算,將手工驗證計算結果與LPLS軟件計算結果進行比較,手工計算結果減去LPLS軟件計算結果的較差統計表見表1所示。
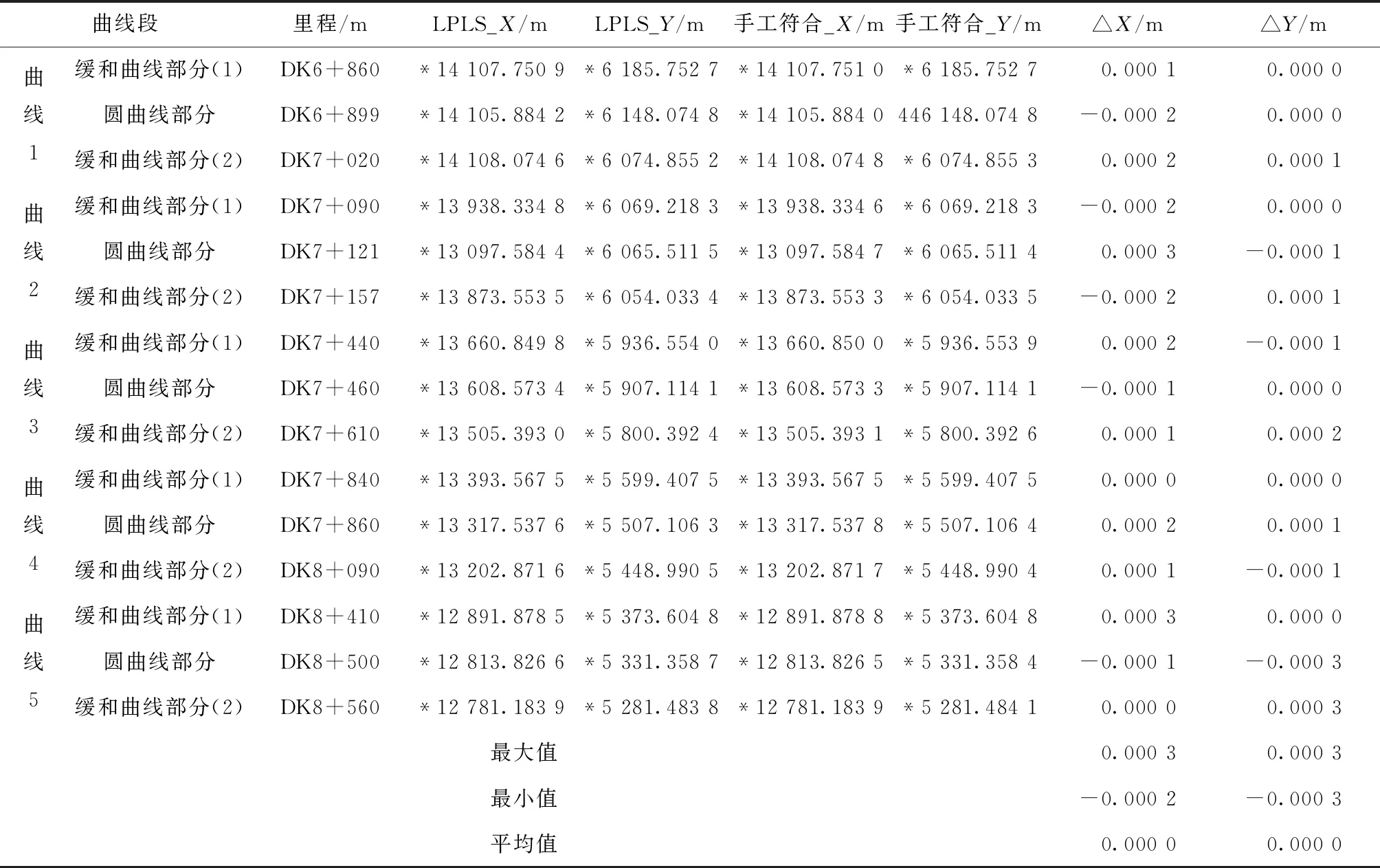
表1 手工計算與LPLS的較差統計表
從表1可以看出,利用本文開發的LPLS軟件計算所截取五段曲線上的里程點中樁平面坐標結果與手工驗證計算結果是一致的(忽略手工計算的取位誤差)。這說明,本文建立的LPLS_H程序模塊是正確的且有效的。
3.2 高程計算
根據高程計算式及計算步驟,基于VS2010開發平臺,利用C#編程語言,建立線路曲線高程計算功能模塊(LPLS_V),基于LPLS軟件計算獲得DK503+500~DK504+436工段的中樁高程計算結果,如圖9所示。
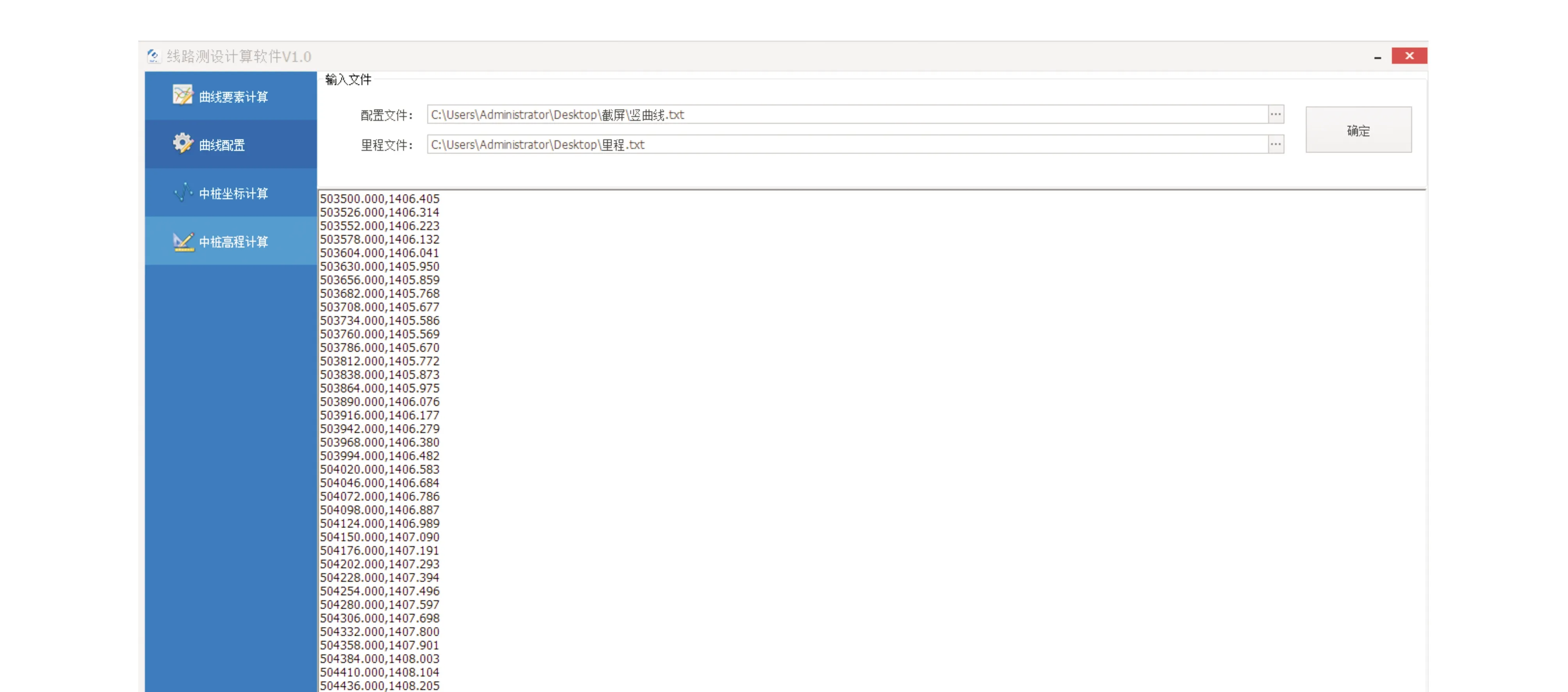
圖9 中樁高程計算結果
如圖9所示,為驗證LPLS軟件計算中樁高程結果的正確性,本文截取變坡點1的里程DK503+750,高程為1405.530 m,半徑為50 000 m,變坡點2的里程DK504+450,高程為1 408.260 m,半徑為50 000 m,變坡點3的里程DK505+980,高程為1 408.72 m,半徑為80 000 m的已知數據進行手工驗證計算,任意選取7個里程點進行作較差分析,手工計算結果減去LPLS軟件計算結果的較差統計表見表2所示。
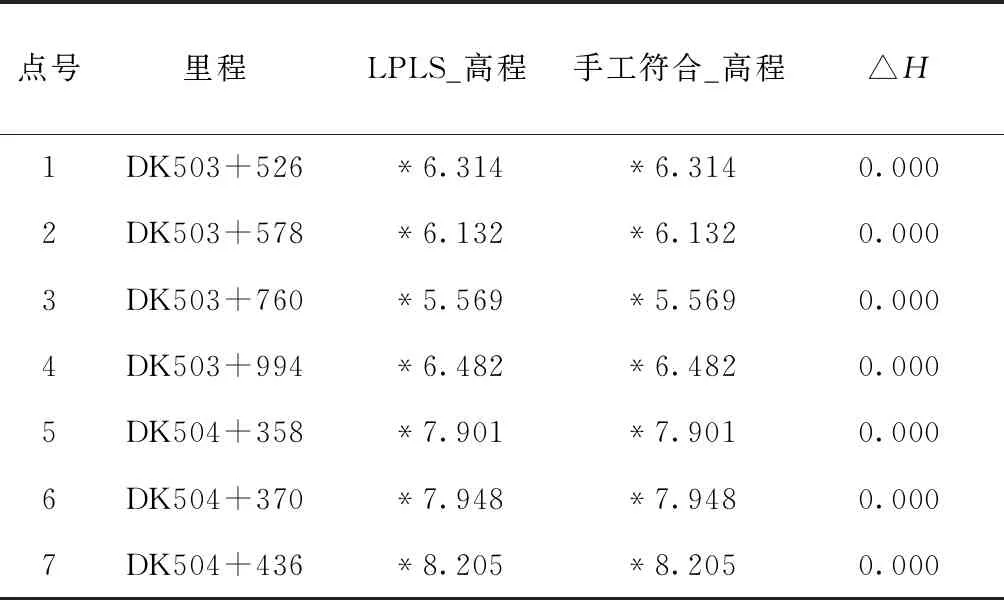
表2 手工計算與LPLS的較差統計表 m
從表2可以看出,利用本文開發的LPLS軟件計算豎曲線上任意選取的7個里程點中樁高程計算結果與手工驗證計算結果是一致的。這說明,本文建立的LPLS_V程序模塊是正確的且有效的。
4 結束語
鑒于線路設計往往是多種類曲線復雜組合,現有工具軟件難以滿足這種組合的點位測設數據計算,本文首先分別推導了圓曲線坐標測設計算模型、帶緩和曲線的圓曲線坐標測設計算模型和豎曲線高程測設計算模型,并利用C#編程語言建立相應的程序模塊(LPLS_H和LPLS_V),基于VS2010開發平臺,設計并開發一種適用于多種類曲線組合的點位測設數據計算軟件(LPLS)。通過某鐵道工程實例的計算驗證,對LPLS軟件的功能模塊的正確性做驗證,實現了線路曲線坐標及高程測設數據計算。本文所設計開發的LPLS軟件,可用于公路、鐵路等線路工程的多種類曲線組合的中樁點位測設數據計算,對提高線路工程的施工放樣和縱斷面設計工作效率具有重要意義和實用價值。

