建筑物立面重復模式的點云投影直方圖分割方法

胡鵬飛，周擁軍

(上海交通大學 船舶海洋與建筑工程學院，上海 200240)

智慧城市、數字地球等概念的提出和應用，使既有建筑物的高精度三維重建成為研究人員關注的重點問題[1]。三維激光掃描技術(LiDAR)通過發射激光并收集從目標反射信息，得到大量三維點云，LiDAR技術因采集速度快、精度高、信息損失少，成為了既有建筑數據采集的主要手段[2]。建筑中存在大量的門、窗、梁、柱等重復模式，這些結構具有共同的幾何形狀和物理參數，隨著BIM技術的廣泛應用，對這些重復模式進行精確重建對BIM建模和分析具有重要意義。本文選擇某建筑物的立面，將窗戶作為重復模式，研究原始點云提取建筑立面后重復模式的提取和高精度重建方法，旨在提高目標提取的速度和精度，為快速構建既有建筑的BIM模型提供理論和方法。

目前，提取建筑物點云輪廓的思路主要有兩種：一種是通過將點云數據根據深度或者強度等信息轉換成二維圖像，然后運用圖像識別的方法來進行輪廓線的提取。趙泉華[3]等人將點云數據轉化成深度圖像，構建一種以非規則圖形為標識隨機模型，對任意形狀的點云外形進行提取。程效軍[4]將三維點云進行切片，分成不同層的平面點云，將每一層點云轉換成圖像，運用圖像處理中的形態學算子提取輪廓，并反求得到點云邊緣特征點。另一種思路則是直接對點云進行輪廓提取，目前使用較為廣泛的方法有凸包算法[5-7]、三角網法[8-10]、AlphaShape算法[11-15]等。此外，一些學者還提出了一些新方法：樊晶晶[16]通過萬向切片得到包含輪廓點的點云數據，定義基于法向量夾角的模式向量，在與模式向量歐氏距離最小的組內提取輪廓。童禮華[17]提出一種改進的輪廓密度估計方法，通過自動計算格網密度閾值，精確提取建筑物輪廓。

雖然目前對于建筑物點云輪廓的研究很多，但是還有不足之處。基于深度圖像的算法雖然利用了成熟的圖像處理技術，但同時也存在以下問題[18]：首先，三維點云轉換成二維圖像的過程必然會丟失一部分空間信息，造成提取精度的降低；其次，由于轉換過程中需要人工對格網進行劃分，不同的劃分方式會導致圖像的分辨率發生變化，影響分割效果；最后，如何將三維點云和二維圖像進行配準也是一個難題。AlphaShape算法和凸包算法比較適用于點云密度比較均勻的情況，對于密度不均勻的情況和某些點云缺失部位容易造成輪廓的誤提取[19]。三角網法得到的結果比較穩定，但是得到的輪廓線邊緣會存在一些狹長的三角形部分，不能準確反映出目標的現實輪廓，從而無法精確提取邊緣點[20]。針對上述問題，并考慮到大多數建筑物由大量的重復幾何構件組成的特點，提出了一種基于投影點云特征直方圖的算法，由于直接使用了目標的幾何特性，該算法簡單、無需進行點云變換、抗噪能力強，且不存在輪廓過度提取現象。

1 基于投影點云特征直方圖的點云語義分割

建筑物主體分為建筑物立面部分和建筑物的內部結構，均存在大量的重復結構，對于建筑物的外立面來說，其主要的重復結構為窗戶，而對于建筑物內部來說，主要重復結構為墻、門、梁、柱等。

本文針對具有規則形狀的大量建筑物重復模式的語義分割問題，提出了一種基于投影點云特征直方圖(Projective Point Feature Histogram, PPFH)的提取方法。該方法考慮了重復結構和墻體的點云分布特點，利用二者在不同方向上的點云密度差異，通過統計直方圖的方法確定重復結構的近似邊緣線，最后完成邊緣的規則化和誤差分析。

本文僅以建筑物立面中的重復模式—窗戶為例介紹本文的算法，建筑物立面及窗戶的算法流程主要由以下步驟組成：

1)將建筑物點云投影至xoy平面，使用PCA方法分析，確定建筑物主方向。同時將坐標軸按照PCA分析結果進行旋轉，完成姿態調整；

2)根據建筑物立面特點，尋找點云密度最大區域，提取建筑物立面；

3)投影至建筑物立面并繪制立面各方向點云分布直方圖；

4)通過窗體與墻面點云分布差異確定窗戶精細邊緣線位置；

5)通過合適的閾值確定邊緣線點；

6)利用混合LS-TLS方法進行邊緣重建和誤差分析。

具體流程圖如圖1所示。

圖1 窗戶精細重建流程圖

1.1 PCA分析確定主方向

由于LiDAR三維掃描時設置的測站坐標系與建筑物立面主方向不一致，因此首先需要確定建筑立面的主方向，即找到建筑物立面與測站平面之間的夾角，采用主成分分析(principal component analysis，PCA)確定其主方向。PCA方法是一種將多個變量降為幾個主要成分并保留原始數據大部分主要信息的統計分析方法，在數據降維、機器學習等方面有重要作用[21]。

本文掃描場景為上海交通大學閔行校區行政B樓某面墻體，該墻體上共有50個大小形狀都相同的窗戶，掃描儀器型號為LEICA P40，其距離掃描精度為1.2 mm+10 ppm，掃描間隔為0.02 m，利用cyclone軟件對該建筑物目標區域進行預處理，粗提取了建筑物的墻面，預處理后原始點云數據的三維視圖如圖2所示。

圖2 原始點云數據三維視圖

設該建筑物點云數據總個數為m，所有數據表示為{xiyizi}(i=1,2,…，m)，由于三維點云的z軸方向垂直于水平面，與測站坐標系z軸方向一致。因此只需將點云投影至xoy平面，投影點的主方向即可表示建筑物立面的方位，為此，只考慮所有點云的平面坐標，將坐標中心化：

(1)

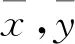
(2)

根據PCA方法原理，散度矩陣S的最大特征值所對應的特征向量即為該建筑物在xoy平面內的主方向。因此，將散度矩陣進行奇異值分解得到特征向量和特征值，其中最大特征值對應的特征向量方向即為建筑物主方向，并計算主方向與原坐標軸之間的夾角θ，并將坐標軸繞z軸旋轉θ，完成建筑坐標變換。轉換前后該建筑物的投影圖如圖3所示，可以看出，經過PCA分析后，點云數據的x，y軸與建筑物的主體方向一致，證明用PCA分析方法尋找建筑物主方向是可行的。

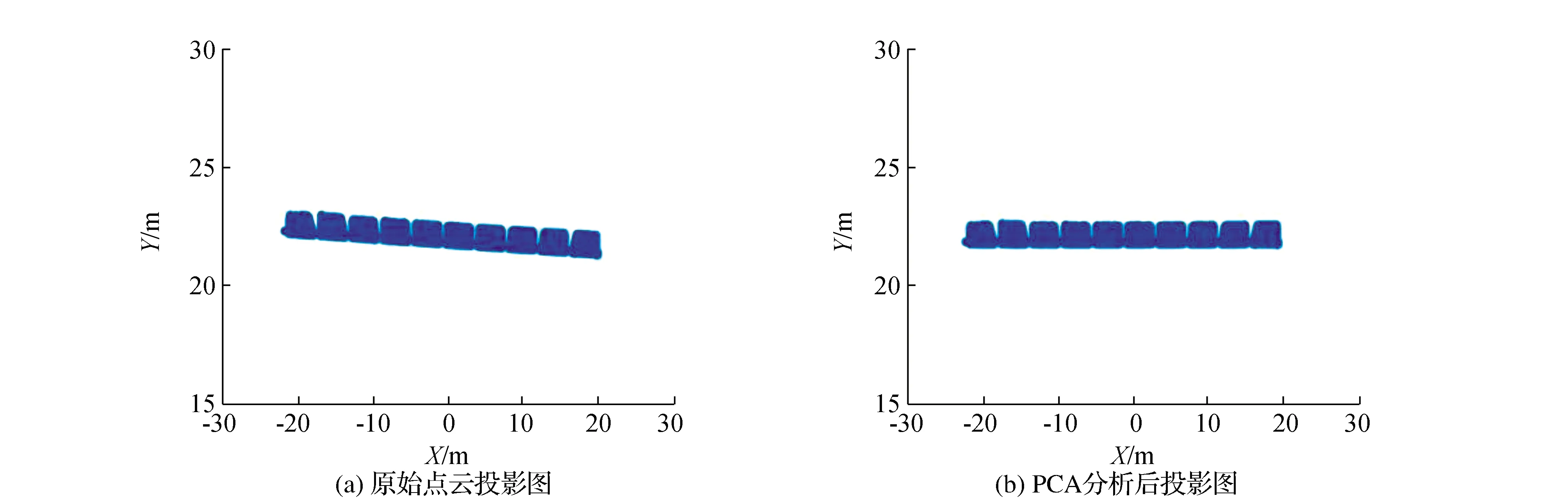
圖3 PCA分析前后投影圖

1.2 建筑物立面提取

為得到窗戶輪廓，首先精確獲得建筑物立面的位置。從建筑物的原始三維視圖可以看出，該建筑物由于事先進行過預處理得到了粗略的建筑物立面，該點云除了建筑物立面外，還包括少量噪聲點以及非立面部分(如窗戶裝飾區域)，由于建筑物立面部分點云密度遠大于其余部分點云密度，為此，可以根據不同部分的點云分布情況精確提取建筑物立面位置。經過PCA分析后的建筑物點云數據投影至xoy平面，如圖3(b)所示，沿著y軸方向劃分為大小相等的若干區間，并統計每個區間內點的數量，繪制點云分布直方圖。直方圖的寬度選擇對于精確提取立面有很大的影響，若選擇較大寬度的直方圖，得到的峰值區間寬度遠大于實際立面寬度，會導致檢測結果不準確。但是如果使用較小寬度的直方圖，那么屬于某一區間的邊緣點可能會落在相鄰的區間內，使每一個區間的觀測值變少，局部極大值在點云分布直方圖中不明顯。因此合理選擇直方圖寬度對提取結果有很大的影響。根據相關規范，一般的框架結構和磚混結構墻體厚度分別為180 mm和240 mm，因此本文取兩者平均值200 mm作為直方圖寬度對該建筑物進行區間劃分，并繪制出統計直方圖，如圖4所示。

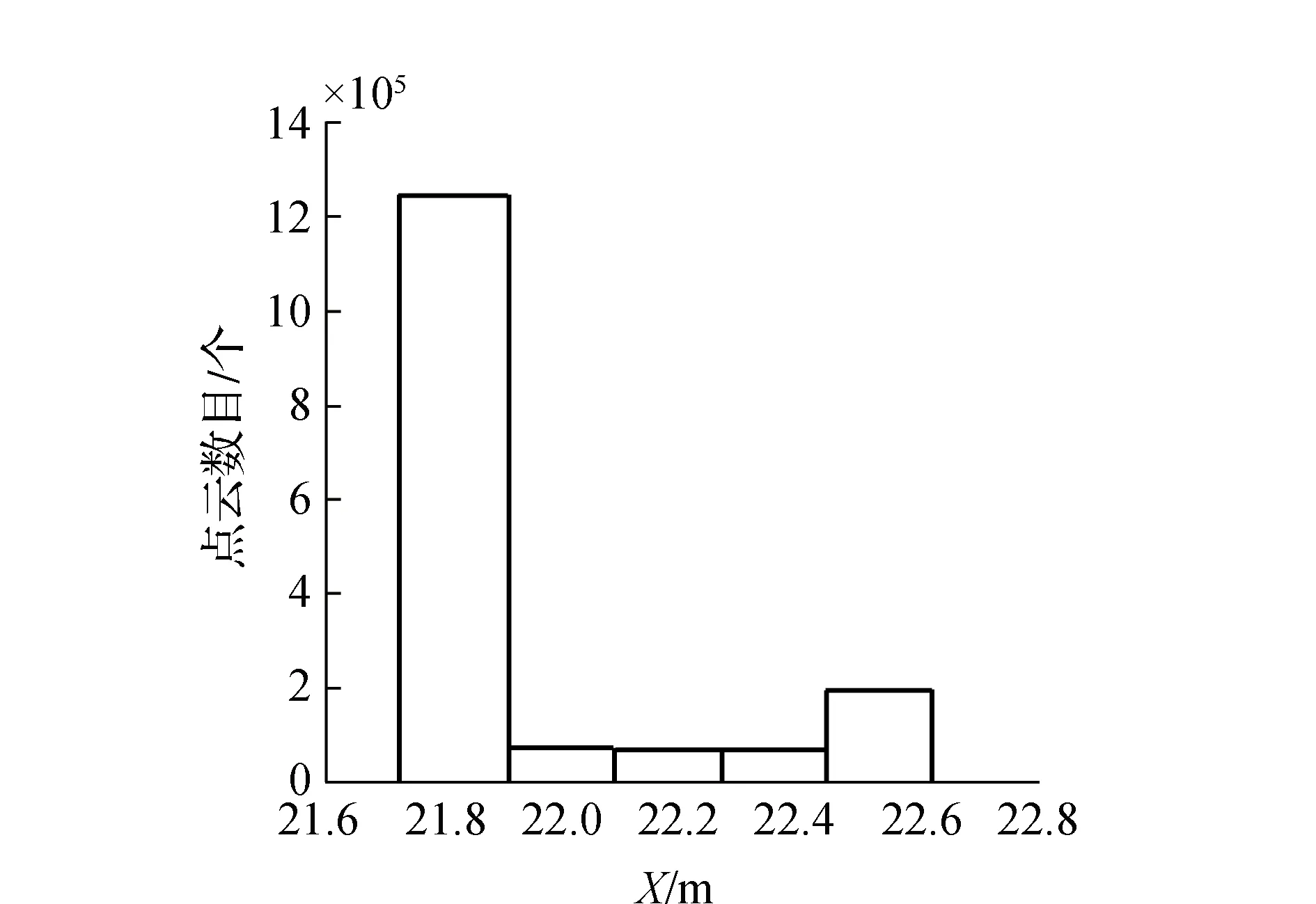
圖4 點云分布直方圖(y方向)

從點云分布直方圖可以看出該建筑物點云在y方向上共有兩個峰值區間，二者之間的距離約為0.6 m，且點云數量遠大于第二個峰值對應的點云數量，因此根據點云結構可以判斷，第一個峰值區間對應建筑物的立面，第二個峰值區間對應窗戶裝飾部分，由于本文僅考慮重建窗戶輪廓，不考慮窗戶其余裝飾區域，因此僅取第一個峰值區間作為建筑物立面點云。

1.3 投影直方圖確定窗戶邊緣線

測量過程中，受窗戶打開或關閉狀態、窗戶和窗簾材質、測量誤差、目標遮蔽等因素的影響，導致窗戶部分的點云數據的空間分布不具備明顯的規律，且大部分的激光會透過窗戶，反射回掃描儀的點云很少，因此，相較于建筑物立面點云來說，窗戶部分的點云密度很小。而窗戶邊緣線作為窗戶與建筑物立面的交界，在點云分布直方圖上必然會出現顯著變化。為此，先將墻體平面投影至建筑物正立面(見圖5)，并對其第一主方向(x軸)和高度方向(z軸)分別劃分若干等間距的區間，分別統計每個區間的點云數目，得到如圖6所示的點云分布直方圖。

圖5 建筑物正立面投影圖

圖6 x，z方向點云分布圖

結合實際情況和投影圖中可知，該建筑物立面存在5個×10個重復結構的窗戶，水平邊緣線共20條，豎直邊緣線10條。這與兩個方向點云分布直方圖所展現的結果相一致，因此，直方圖中極值點左右兩側對應窗戶的邊緣線。

1.4 窗戶邊緣點云提取

邊緣線坐標可以計算得每個窗戶邊緣四個角點的粗略坐標，坐標附近一定區域的選擇即可獲得窗戶邊緣的點云數據。獲取點云數據時，掃描間隔為0.02 m，對于任意一條邊緣線，將邊緣線橫縱方向各偏移0.02 m，得到一個矩形區間，任意落在該區間內的點，即可視為該邊緣線上的點。為了比較不同閾值對后續重建精度的影響，隨機選擇某窗戶進行對比試驗，圖7為閾值0.02 m和0.04 m的邊緣點云圖，將左邊緣線標記為1號直線，逆時針分別為2、3、4號，對于閾值0.02 m的情況，四條邊點數目分別為92、61、92、173，對于閾值0.04 m的情況，四條邊點數目分別為210、183、206、298，根據后續的精細化重建結果得出兩種取值方法對于精細重建的結果影響不大，但是小的閾值選取可能會造成某些邊緣線上的點數據過少，而若繼續擴大閾值，則對重建結果會產生較大影響。因此，對于規則形狀的重復窗戶邊緣線提取，閾值宜取兩倍的掃描間隔。

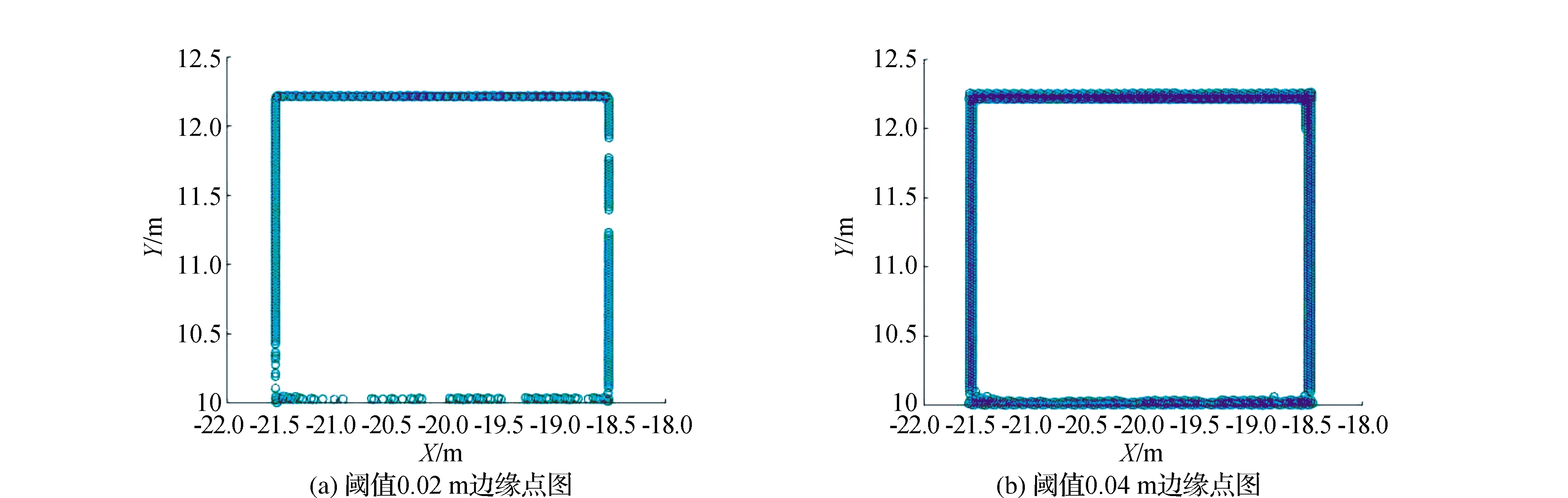
圖7 不同閾值的邊緣點圖

1.5 輪廓提取效果對比

為了驗證本文提出的PPFH算法輪廓提取效果，將本文方法與基于深度圖像的方法和基于AlphaShape算法對比。對于深度圖像方法，將三維點云整個區域投影至xoz平面，劃分為500像素×500像素大小的網格，采用(Inverse Distance Weighted，IDW)內插方法確定每個網格的特征灰度值，將其轉換為二維灰度圖像，隨后使用Canny算子進行邊緣檢測，提取對應的邊緣點云。對于Alpha-Shape算法，取α=2.5 cm對該三維點云數據進行輪廓提取。圖8展示了本文算法(PPFH)、基于深度圖像的方法和Alpha-Shape算法所提取結果(本文算法僅提取窗戶邊緣)。

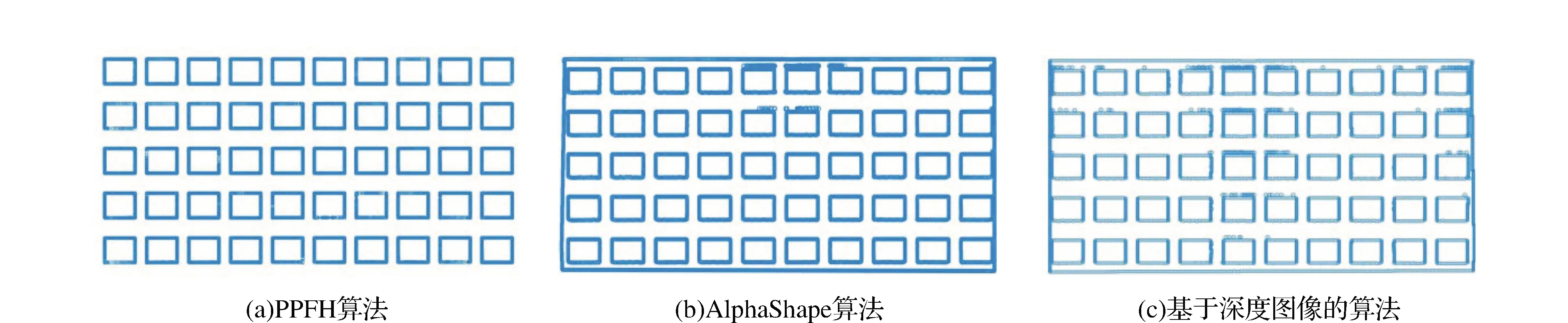
圖8 窗戶提取結果

通過對比3種算法可以獲得50個窗的基本輪廓，但是基于深度圖像的方法和AlphaShape算法過度提取窗戶邊緣線，AlphaShape算法通過設置alpha半徑提取輪廓線，在窗戶邊緣部分遮擋的情況下會將缺失區域確定為邊界，從而影響提取效果，而基于深度圖像的提取算法需要將點云轉換為圖像，除容易在點云缺失區域存在邊緣誤提取之外，相互轉換既增加數據處理的復雜度也降低提取精度。而本文提出的PPFH方法直接利用建筑物的常見幾何特性，無需對原始點云進行壓縮和變換，算法原理簡單，輪廓提取準確，對存在邊界遮蔽的情況下也能準確提取，具有較好的實用性。

2 邊緣規則化與誤差分析

成功提取邊緣點后，為實現邊緣輪廓的高精度重建，本文采用文獻[22]中提出基于EIV模型的混合LS-TLS方法來解決二維直角建筑物的邊界重建問題。該方法采用了海森法和正交距離法代替了傳統的斜截式表示直線方程，綜合考慮建筑物的幾何關系以及測量誤差，構造建筑物含誤差模型，并使用混合LS-TLS的解算方法。

窗戶模型共由4條相互正交的邊緣構成，假設θ表示左側邊緣線的法向對應的坐標方位角，ρi，i=1,2,3,4分別表示坐標原點到窗戶四條邊緣線的距離。由于相鄰窗戶邊緣線之間相互垂直，則窗戶的函數模型表達式為：

(3)

式中：xij，yij分別表示第i(i=1,2,3,4)條邊緣線上第j個點的坐標，βx=cosθ，βy=sinθ。利用混合LS-TLS方法可以解出窗戶邊緣線的距離參數ρ=(ρ1，ρ2，ρ3，ρ4)T和角度參數β=(βx，βx)T，窗戶的長寬：

l=|ρ1-ρ3|，

d=|ρ2-ρ4|.

(4)

獲得窗戶的幾何參數后，利用近似的精度估計方法計算得到角度參數和邊緣線距離參數的理論協因數陣，根據誤差傳播原理[23]可以得出每個窗戶幾何參數所對應的理論協因數陣應滿足：

(5)

根據單個窗戶的幾何參數和誤差分析結果可以判斷出這50個窗戶屬于同一類窗戶，隨后將計算所得的50個窗戶的幾何參數進行統計分析，取50個窗戶的平均值作為此類重復窗戶的共同參數，計算對應的長度、寬度的均方根。長、寬均方根為：

(6)

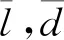
所有邊緣線點進行重建和誤差分析，結果如表1所示，分析數據可知：PPFH方法得到的窗戶平均幾何參數為：長3.029 3 m，寬2.186 7 m。單個窗戶角度平均誤差±0.000 3°，最大誤差±0.000 9°，長度平均誤差±6.6 mm，最大誤差±16.4 mm，寬度平均誤差±5.7 mm，最大誤差±10.6 mm，統計所得長度均方差0.009 4 m，寬度均方差0.008 8 m，所得結果優于AlphaShape算法和基于深度圖像的方法。

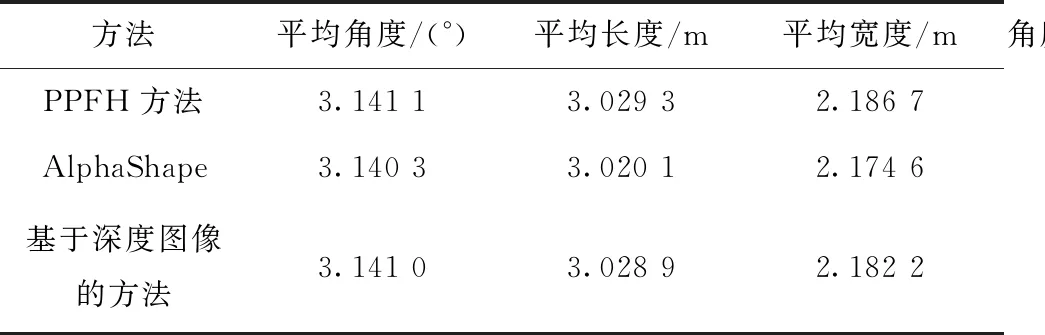
表1 3種方法窗戶的幾何參數及誤差

根據相關規范，結合統計分析結果可判斷建筑物窗洞口尺寸為3 m×2.1 m，根據現場勘查判斷，長寬誤差主要以下原因造成的：首先，在建筑物裝修過程中需要對外墻進行抹灰，通常來說單邊間隙為1.5 cm；其次施工過程中和測量過程均會由于各種原因產生一定的誤差，本文所得的長寬誤差在容許范圍之內，因此本文將窗戶的平均值作為窗戶的共同幾何參數的方法，大大提高精度，反映窗戶的實際情況。

3 多樣重復模式提取研究

在實際場景之中，建筑物的重復結構相對比較復雜。對于多層建筑物，建筑物外立面的重復模式的大小、位置、類型會隨著樓層的變化而改變，如建筑物底樓的立面往往存在門等結構。為解決這一問題，可先將建筑物逐層分割，將復雜的三維點云投影或切片變為平面點云后，通過本文的方法提取重復特征。對建筑物原始點云的分層處理不僅可以在保留特征的前提下提高特征提取的準確度，而且能大幅減少計算的工作量。多層建筑樓板附近的點云密度比其余部分大，因此可以根據點云在豎直方向的統計直方圖作為分層的依據。

圖9展示了某一工廠某外立面的提取過程：圖9(a)為該工廠的原始點云三維視圖，該工廠主體共三層，共細分為7個建筑物立面。其中最左側立面每一層的重復模式不同，因此選取該立面為算例，驗證本文算法對不同樓層的重復模式的提取效果。根據本文的算法，先確定建筑物的主方向，然后根據給定閾值對其進行豎向切片，并對得到的切片按高程進行統計分析，得到圖9(b)所示的直方圖，其中各峰值點代表該建筑物各層樓板位置。得到樓板的位置后，將立面點短根據樓板位置分割，并得到每一層的點云直方圖，圖9(c)、9(d)、9(e)分別為各層的點云直方圖。本算例的重復模式主要是門窗，從圖中可以看出一、二樓各有4個重復結構，三樓有2個重復結構。最后，對各樓層按本文方法對其進行精確提取，得到該工廠立面的重復模式提取結果如圖9(f)所示，其中，紅色結構為門，藍色結構為窗。

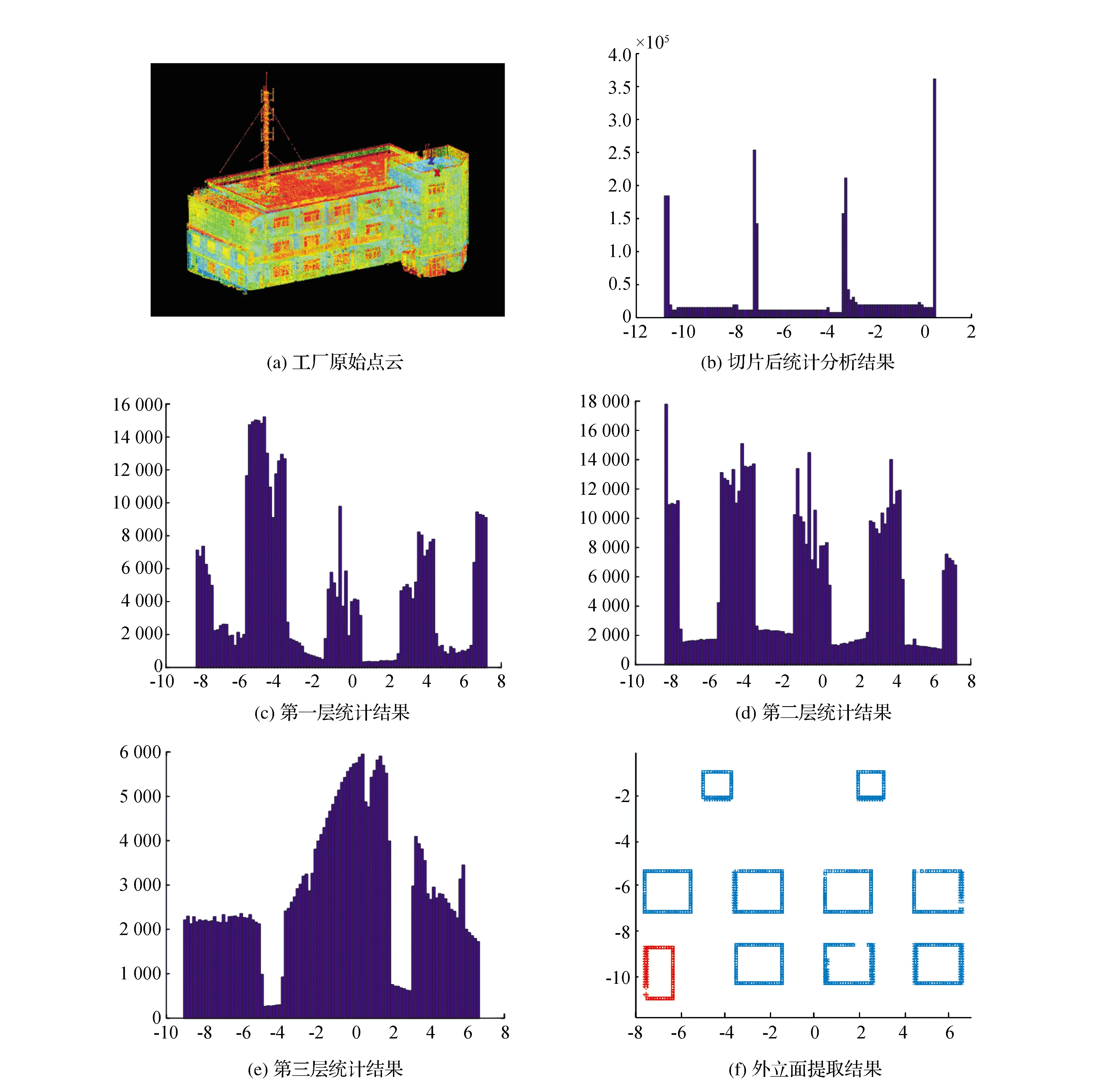
圖9 工廠立面提取示意圖

建筑物內部的重復模式主要是梁、柱、墻、門等，不同的重復模式其法向量有不同的特點，如梁的法向量與水平面垂直。柱、墻的法向量都與水平面平行，但由于柱的長寬比一般較小，所以其法向量與x，y主方向的夾角都比較小，而墻體往往只有一個方向夾角較小。對比不同重復模式的法向量特點，可以初步得到重復模式的基本類型，并實現重復模式的粗分割。最后，通過對粗分割結果的平差計算，可以得到精確的重建結果。

4 結束語

本文針對現代建筑中大規模存在的形狀規則的重復結構，通過PCA方法確定主方向，結合目標物的幾何特性和點云的統計規律對結構輪廓進行高精度的語義分割，同時利用混合LS-TLS方法實現邊界的規則化和誤差分析。通過算例分析表明本文的方法在提取形狀規則的重復結構目標的準確度和精度都優于現有的AlphaShape算法，可以廣泛應用于對規則重復結構的提取。由于本文的方法利用了重復模式的正交和平行等幾何特性，因此主要適用于矩形形狀的目標提取，之后的研究應該針對其他復雜結構的提取，以提高算法的適用范圍。