基于動力學性能的更高速度鐵路合理線間距研究
付連著 李紅艷 孫加林 李紅梅
(1.鐵科院(深圳)研究設計院有限公司,廣東深圳518055;2.中國國家鐵路集團有限公司鐵路基礎設施檢測中心,北京100081;3.中國鐵道科學研究院集團有限公司基礎設施檢測研究所,北京100081;4.中國鐵道科學研究院集團有限公司鐵道科學技術研究發展中心,北京100081)
鐵路運輸的高速化是世界各國鐵路技術發展的方向。隨著列車運行速度的提高,列車高速交會引起列車之間的氣流劇烈擾動,產生的瞬態壓力沖擊對列車運行安全性和旅客舒適性帶來不利影響。
為了分析列車交會時氣動效應引起的動力學問題,相關學者開展了大量工作。何德華等[1]利用列車空氣動力學和車輛動力學相結合的方法研究了動車組明線交會時氣動力對車輛動力學的影響。王一偉等[2]研究了隧道壓力波的形成和峰值影響因素,推導了壓力極值對應的最不利隧道長度關于列車長度、運行馬赫數的表達式。郗艷紅等[3]提出了明線等速交會時車體表面壓力波幅值變化的新公式。梁習鋒等[4]研究了不同線間距下高速列車交會時的壓力波特性。喬英俊等[5]闡述了線間距與列車交會壓力波之間的理論關系,并根據實測和數值仿真數據得出了壓力波與線間距之間的擬合曲線。魏洋波等[6]采用滑移網格技術對高速列車明線交會及隧道內交會時的空氣流場進行數值模擬,研究了不同線間距對高速列車交會壓力波的影響。
上述研究均基于既有線路的設計時速,不超過350 km。為了做好列車進一步提速的技術儲備,有必要對我國高速鐵路列車交會試驗數據進行綜合分析,研究列車進一步提速后的空氣動力學效應和車輛動力學性能。本文建立了明線交會和隧道內交會的空氣動力學模型及車輛動力學模型,研究不同車速、不同線間距條件下列車交會時所受的風壓變化規律及其對車輛動力學的影響規律,為確定更高速度下的鐵路線間距提供參考。
1 計算模型
1.1 空氣動力學模型
選取CRH380A型列車作為研究對象,根據車輛實際結構,采用成熟的商業計算流體軟件FLUENT建立三維實體列車空氣動力學模型,如圖1所示。建模時在計算精度允許的前提下,對車輛進行了適當簡化。為了提高網格質量、計算精度和效率,全部部件均采用結構化網格。
圖1 CRH380A型動車組三維實體空氣動力學模型
列車交會屬于非定常問題。為模擬交會列車之間的相對運動,計算區域采用分區對接網格技術,地面、列車均采用六面體結構化網格離散。各分區之間通過公共滑移界面進行數據交換。計算模型離散后的體網格總數均在1 000萬以上。動車組明線交會及隧道內交會的空氣動力學計算模型如圖2所示。
圖2 動車組交會空氣動力學計算模型
1.2 車輛動力學模型
根據CRH380A型列車的實際結構,采用UM車輛動力學仿真軟件建立車輛動力學模型。單編組車輛模型由1個車體、2個構架、8個軸箱、4個輪對構成,輪對和構架通過一系懸掛單元連接,構架與車體之間通過二系懸掛單元連接,如圖3所示。

圖3 車輛動力學模型(單編組)
1.3 動力學評價指標
根據GB/T 5599—2019《機車車輛動力學性能評定及試驗鑒定規范》,脫軌系數和輪重減載率的限值均為0.8;輪軸橫向力H應滿足H≤15+P0/3,其中,P0為靜軸重,kN。
根據《高速鐵路線路維修規則(征求意見稿)》,車體橫向加速度不大于0.10g,車體垂向加速度不大于0.15g,Sperling平穩性指標控制在2.5以下,評級即為優秀。
2 模型驗證
選取8編組CRH380A型動車組進行隧道內交會的實車試驗。動車組長約203 m,線間距為4.4 m;隧道斷面面積81.37 m2,長863 m。交會地點為隧道中心,車速v=300 km/h。
將實車試驗的參數輸入仿真模型進行計算,得出交會壓力波時程曲線,并與實車試驗結果進行對比,見圖4。可知:仿真計算與實車試驗的交會壓力波變化幅值基本一致;實車試驗的壓力波變化曲線波動較大,這是因為實車試驗考慮了車輛真實結構、列車振動、氣候環境等因素的影響。
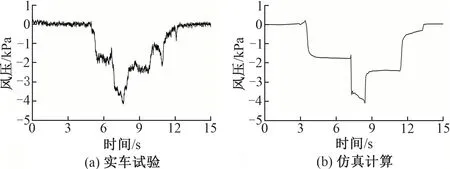
圖4 隧道內交會的壓力波時程曲線對比
仿真計算結果和實車試驗結果吻合較好。因此,該仿真模型能夠比較準確地反映動車組交會時的壓力波變化規律。
3 工況分析
為充分考慮交會車輛之間的相互作用,建立8節車輛編組的動力學仿真模型。編組情況為:第1車、第4車、第5車、第8車為拖車,其余為動車。從車頭到車尾均布64個監控點,監控點位于車窗高度位置。
將空氣動力學仿真計算輸出的力和力矩輸入到車輛動力學模型進行仿真模擬,分析動車組在明線交會及隧道內交會時產生的空氣壓力波對車輛動力學性能的影響。
3.1 明線交會
動車組分別以v=350,400,450,500 km/h在明線交會時,車身風壓隨縱向位置的分布見圖5。
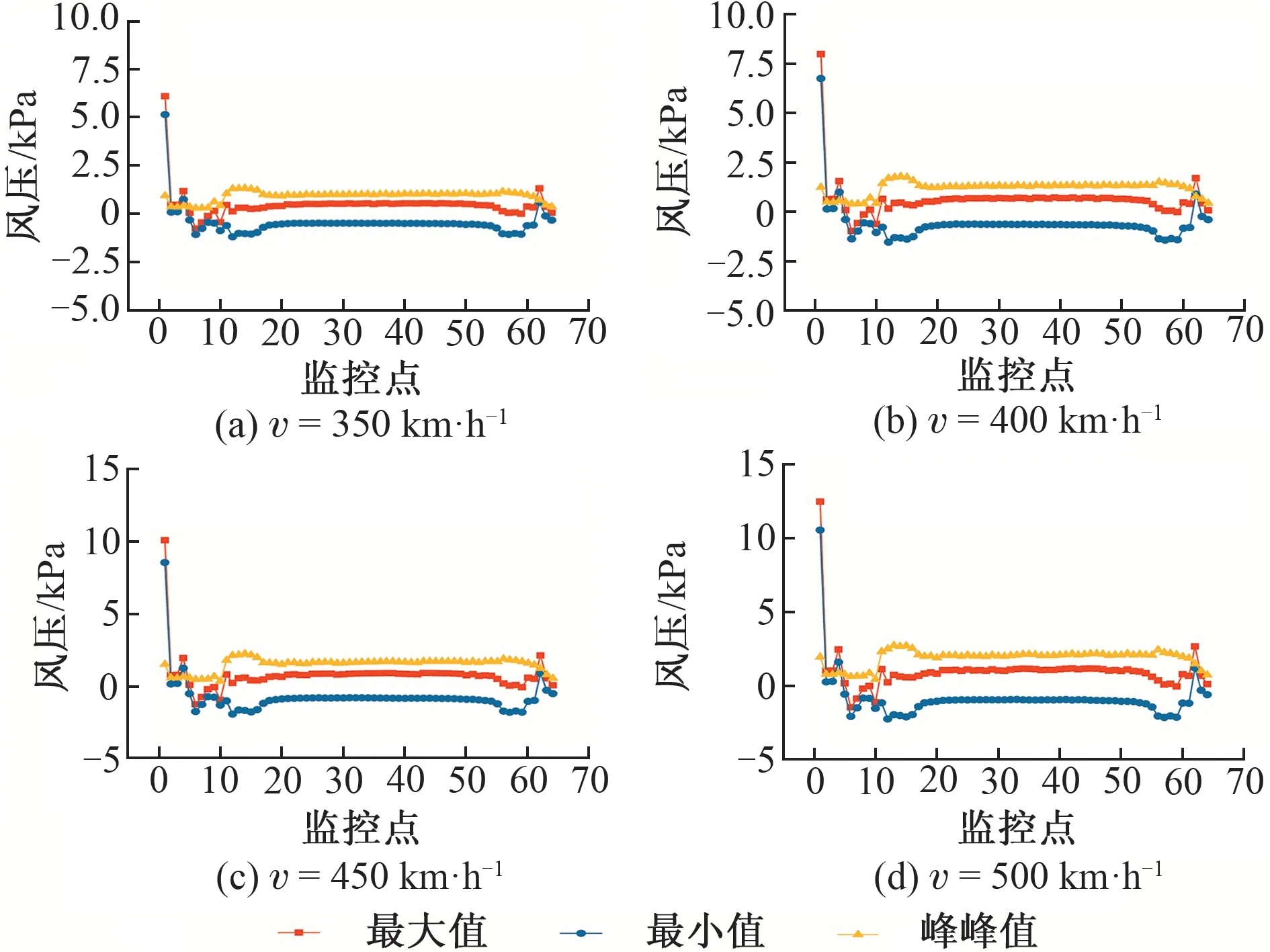
圖5 不同速度級下明線交會時車身風壓分布
由圖5可知,動車組以不同車速在明線交會時:①車輛全身所受風壓最大值均出現在車頭;②車頭所受風壓最大值均出現在車頭前端,而車尾所受風壓最大值均出現在車尾后端,這與車頭和車尾復雜的形狀有關;③車廂所受風壓比較均勻,每節車廂所受風壓最大值差別不大。
取線間距h=5 m,計算動車組以不同車速在明線交會時的車體表面平均風壓,并擬合車體表面平均風壓與車速的關系曲線,見圖6。
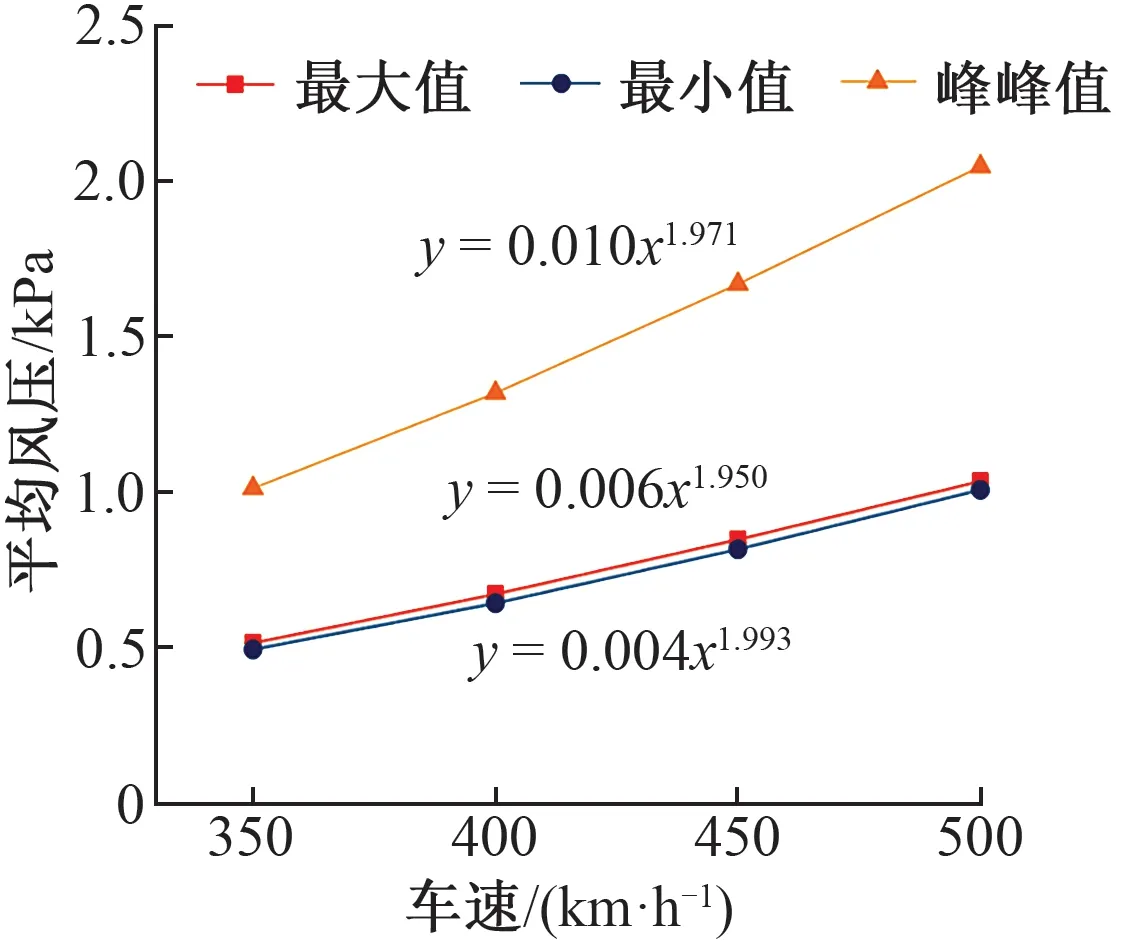
圖6 明線交會時車體表面平均風壓與車速的關系曲線
由圖6可知,動車組在明線交會時:①車體表面平均風壓的最大值、最小值、峰峰值均隨著車速的增加而增大,v=500 km/h時車體表面平均風壓的最大值、最小值、峰峰值比v=350 km/h時分別增大了106.6%,104.7%,102.4%;②車體表面平均風壓與車速的2.0次方成正比。
分別取線間距h=5.0,5.2,5.4 m,計算動車組以v=500 km/h在明線交會時的車體表面平均風壓,并擬合車體表面平均風壓與線間距的關系曲線,見圖7。
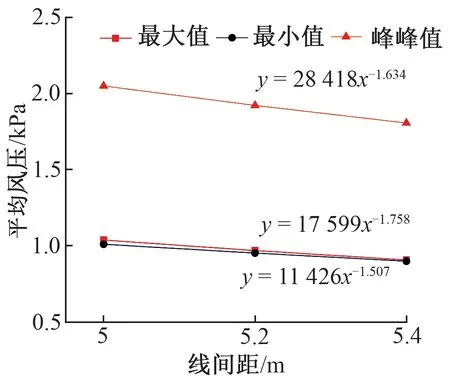
圖7 明線交會時車體表面平均風壓與線間距的關系曲線
由圖7可知,動車組在明線交會時:①車體表面平均風壓的最大值、最小值、峰峰值均隨著線間距的增加而減小,h=5.4 m條件下車體表面平均風壓最大值、最小值、峰峰值比h=5.0 m條件下分別減小了14.4%,12.3%,13.4%;②車體表面平均氣動載荷與線間距的-1.5~-2.0次方成正比。
不同線間距條件下動車組以不同速度在明線交會時的車輛安全性、平穩性指標見表1、表2。可知:
1)同一車速條件下,車輛安全性、平穩性指標均隨線間距的增大而減小。
2)對于v=350 km/h,動車組的各項指標在各線間距條件下均能滿足要求;對于v=400,450 km/h,動車組在線間距h=5.0 m條件下能夠安全平穩運行;對于v=500km/h,各線間距條件下均有動力指標超出安全限值。因此,建議動車組明線交會時的運行速度控制在450 km/h以下。
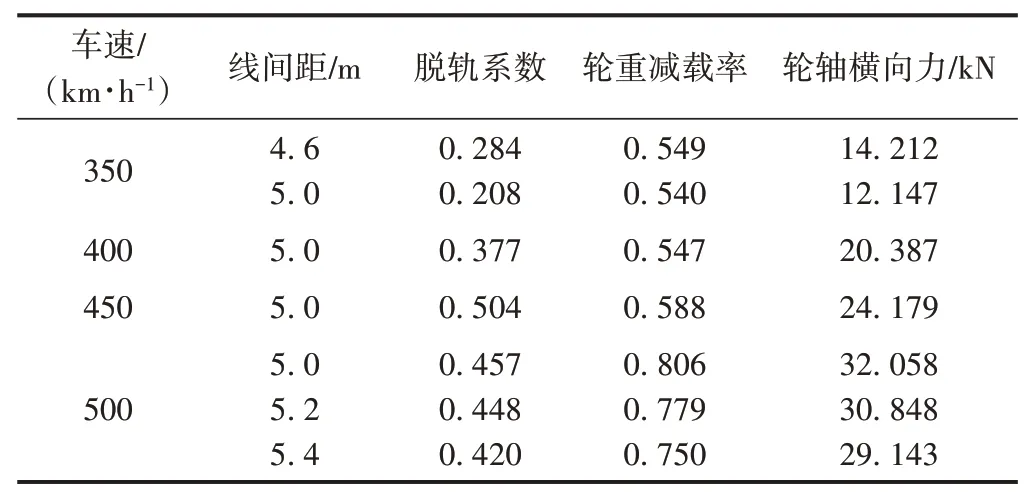
表1 明線交會時車輛安全性指標
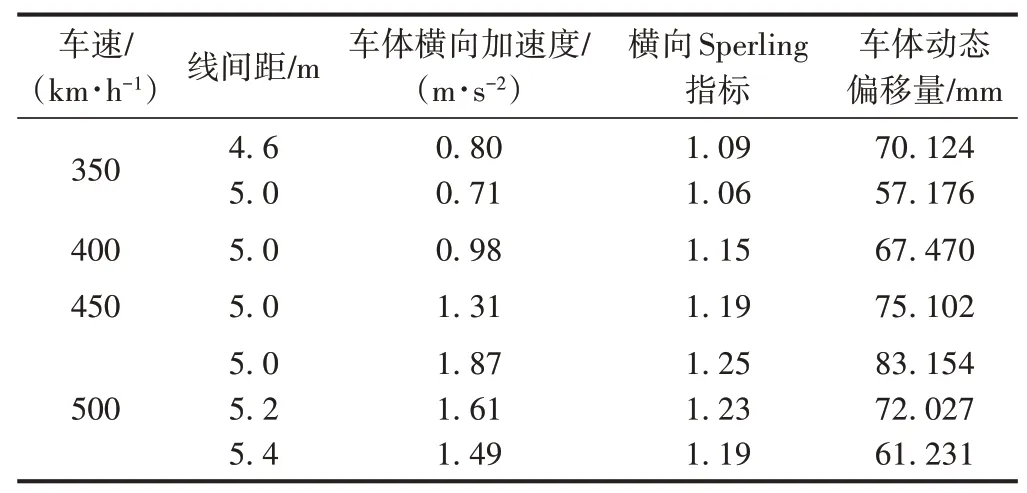
表2 明線交會時車輛平穩性指標
3.2 隧道內交會
車速是影響動車組在隧道內交會時氣動效應的主要因素之一。取隧道有效凈空面積為100 m2,線間距為5.0 m。動車組以v=350,400,450,500 km/h在隧道內交會時,車身風壓隨縱向位置的分布見圖8。
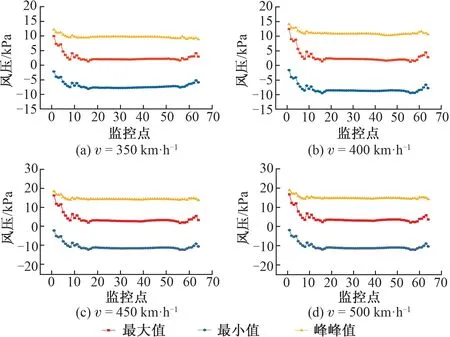
圖8 不同速度級下隧道交會時車身風壓分布
由圖8可知,動車組在隧道內交會時:①車輛全身風壓最大值出現在車頭;②車頭所受風壓最大值出現在車頭前端,而車尾所受風壓最大值出現在車尾后端,這與車頭和車尾復雜的形狀有關;③車廂風壓分布有一定差異,靠近車頭的車廂所受風壓最大,靠近車尾的車廂所受風壓最小。
計算動車組在各速度級下進行隧道內交會時的車體表面平均風壓和中心隧道壁瞬變壓力,并分別擬合其與車速的關系曲線,見圖9、圖10。
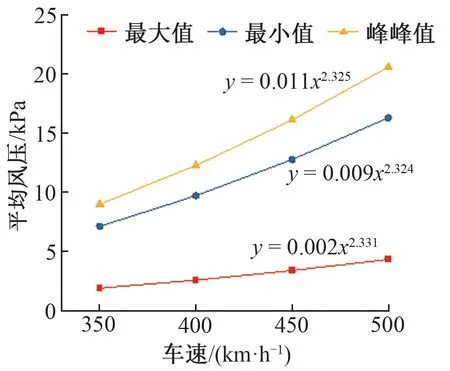
圖9 隧道內交會時車體表面平均風壓與車速的關系曲線
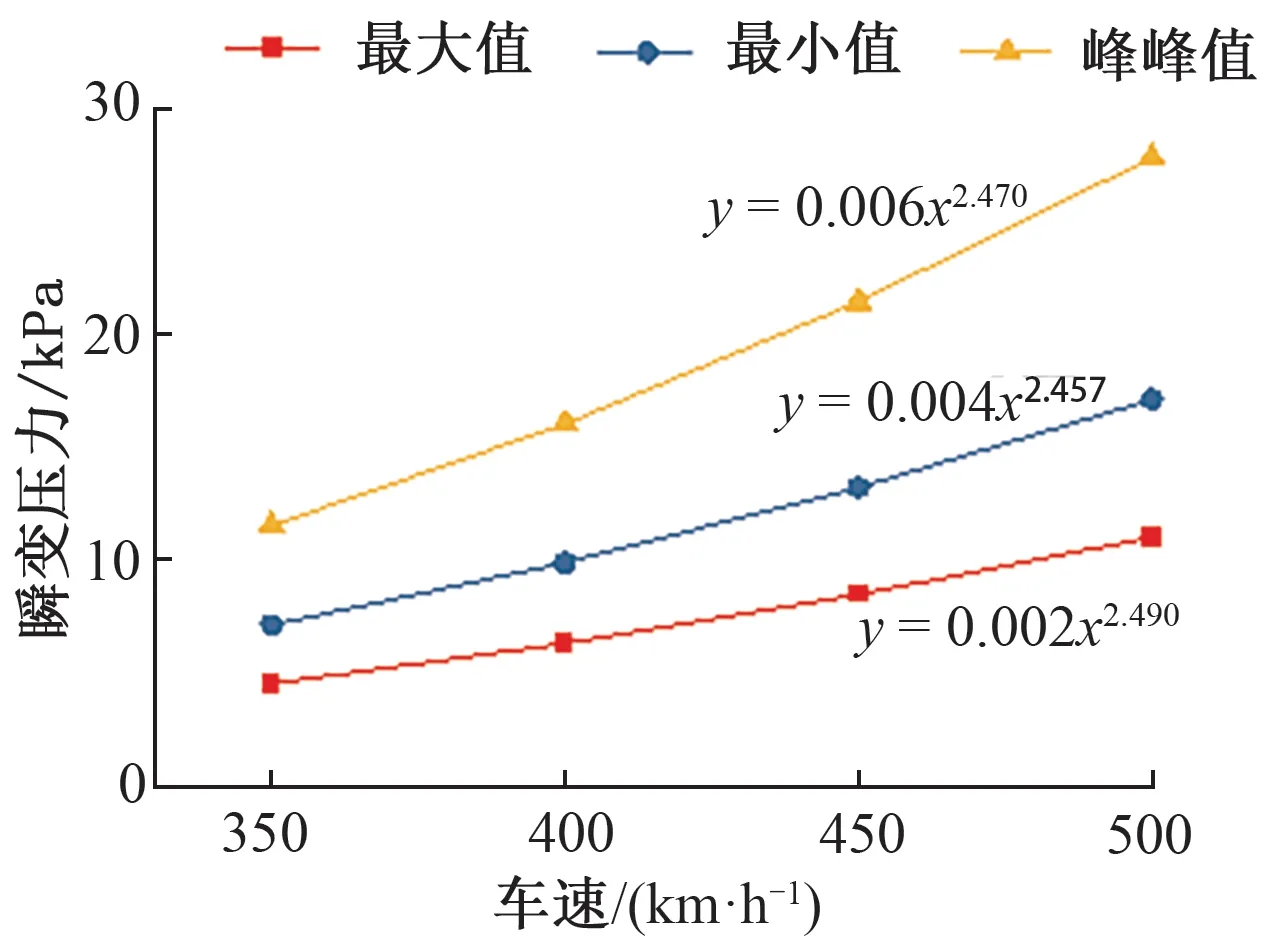
圖10 隧道內交會時中心隧道壁瞬變壓力與車速的關系曲線
由圖9、圖10可知,動車組在隧道內交會時:①車體表面所受的平均風壓最大值、最小值、峰峰值與車速的2.3次方成正比;②中心隧道壁所受的瞬變壓力最大值、最小值、峰峰值與車速的2.5次方成正比。
不同隧道斷面面積、不同線間距條件下,動車組以不同速度在隧道內交會時的車輛安全性、平穩性指標見表3、表4。
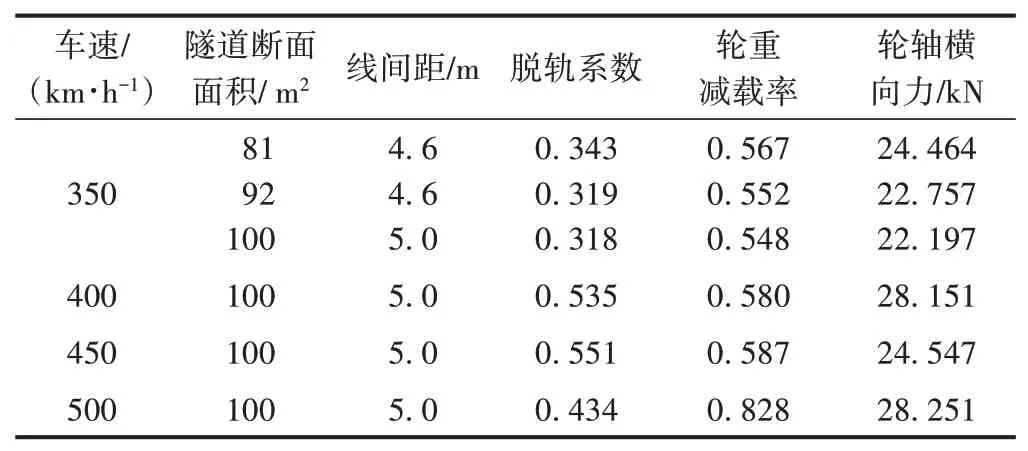
表3 隧道內交會時車輛安全性指標
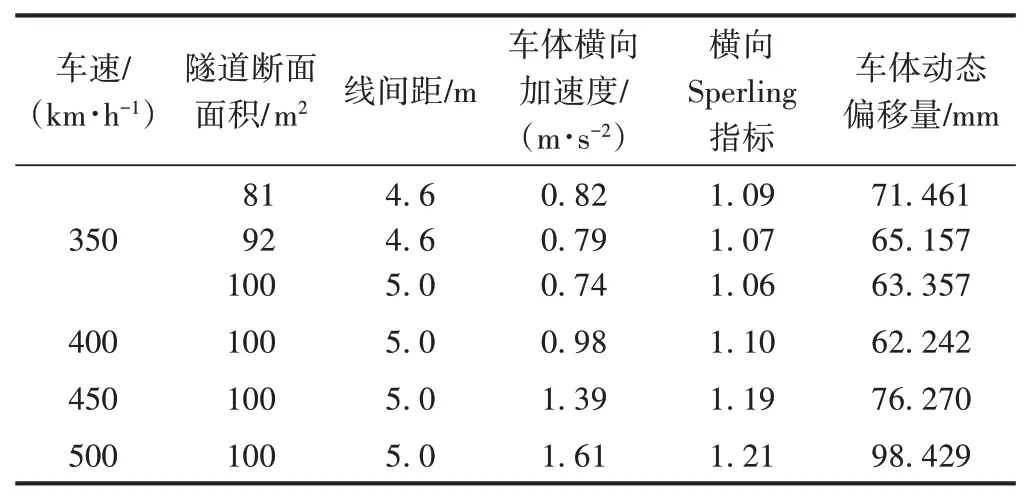
表4 隧道內交會時車輛平穩性指標
由表3、表4可知:
1)v=350 km/h時,動車組在各隧道斷面面積及線間距條件下均能安全平穩運行。
2)在隧道斷面面積為100 m2、線間距為5.0 m條件下,動車組以v=400,450 km/h在隧道內交會時各項安全性、平穩性指標均滿足限值要求;v=500 km/h時脫軌系數、輪軸橫向力滿足安全性要求,而輪重減載率、車體橫向加速度均超過限值,可能會發生瞬間晃車、脫軌等。
4 結論與建議
1)動車組在明線交會時,車頭部位尤其車頭前端所受風壓最大,各車廂之間所受風壓差別不大;動車組在隧道內交會時,車頭部位尤其車頭前端所受風壓最大,車廂風壓分布也有差異,靠近車頭的車廂所受風壓最大,靠近車尾的車廂所受風壓最小。
2)動車組以350~500 km/h的運行速度在明線交會時,車體表面所受風壓極值與運行速度的2.0次方成正比;動車組以350~500 km/h的運行速度在隧道內交會時,車體表面所受風壓極值與運行速度的2.3次方成正比。
3)對于2種交會工況,相同速度級下的車輛運行安全性、平穩性指標均隨線間距、隧道斷面面積增大而減小。
4)考慮到車輛運行的各項安全性、平穩性指標限值及建設成本,對于設計時速350 km的線路,建議線間距取4.6 m;對于設計時速400~450 km的線路,建議線間距取5.0 m。

