飛機結構件槽腔內面間最短距離計算算法
胡寶瑩,張天陽,鄭國磊,周 敏
飛機結構件槽腔內面間最短距離計算算法
胡寶瑩1,張天陽2,鄭國磊3,周 敏4
(1. 沈陽飛機工業(集團)有限公司,遼寧 沈陽 110034; 2.中國航天系統科學與工程研究院,北京 100048; 3. 北京航空航天大學機械工程及自動化學院,北京 100191; 4. 中國農業大學工學院,北京 100083)
在飛機結構件數控加工自動編程系統的開發過程中,由于零件的特征層面的工藝性缺陷,特別是槽腔內面間的最短距離過小,容易導致零件加工復雜、成本過高甚至無法加工。目前針對該模型問題主要采用人工檢查的方式,不僅效率低且易出錯。針對具有復雜形狀,并且包含開閉角、內陷等復雜特征的飛機結構件槽腔,其側壁面間最短距離無法直接獲取的問題,提出飛機結構件槽腔內面間最短距離計算算法。首先給出槽腔以及與距離相關的術語定義,接著在特征幾何參數提取的基礎上,將側壁面間最短距離計算轉化為線線間最短距離計算,并根據槽特征的幾何特性提出線線距離有效性判斷準則以簡化計算,求得槽特征內側壁面間最短距離。最后,以某飛機結構件模型為例,驗證了該算法的可行性和有效性。
最短距離;工藝性;數控加工自動編程;飛機結構件;槽腔
在現代飛機設計中,為滿足高性能的要求,廣泛采用性能優越的整體結構件[1]。整體結構件作為飛機主要承力構件以及保證氣動外形和結構準確度的結構,通常具有結構尺寸大、結構復雜、制造精度要求高等特點[2-3],其數控程序編制效率與質量是影響其加工效率與質量的關鍵因素。在飛機結構件數控加工自動編程系統的開發過程中,由于零件的特征層面的工藝性缺陷,槽腔內面間的最短距離過小,容易導致零件加工復雜、成本過高甚至無法加工[4-5],從而不能形成正確有效的工藝方案[6-8]。目前針對該模型問題主要采用人工檢查的方式,不僅效率低而且易出錯[9]。在數控加工領域,相關的有最小通道計算問題,主要有偏置法[10]和基于Voronoi Mountain的方法[11-12],均不能直接用于本文問題的求解。因此,本文探究一種快速求解飛機結構件槽腔內面間最短距離的算法,并開發出一套自動檢測系統,對航空制造業實現快速數控編程有著重要的現實意義。
1 術語定義
為了便于算法的描述,首先介紹與該算法相關的術語。
1.1 槽 腔
將平面槽腔表示為F,其示意圖如圖1(a)所示。F定義為
F=F∪F∪F∪F∪F∪F(1)
其中,F,F,F,F,F,F分別為腹板、底角、側壁、轉角、內陷和頂面。為了便于算法描述,將腹板和底角統稱為底面,記為F;將側壁、轉角和內陷統稱為槽側面[13],記為F,則有
F=F∪F
F=F∪F∪F(2)
F= F∪F∪F
F的結構可以用環L表示(圖1(b)),即將槽腔底面F投影到腹板b。其中,最外圍的環稱為外環,記為l,定義逆時針方向為內環的正方向;將外環所包圍的環稱為內環,記為l,內環的集合記為L,定義順時針方向為內環的正方向,則L可表示為
L=l∪L(3)
1.2 側面的頂邊集與底邊集
對于F內任意側面F,F與頂面F的公共邊集在腹板F的投影稱為F的頂邊集,記為Ei,F與F的公共邊集在F的投影稱為F的底邊集,記為E。易知F,E,E三者是一一對應的關系。
易知E?L,則對于側面F∈F,存在唯一的一個邊集E?L與其對應,此時E=E,將該單射關系記為,則有
(F)=E(4)
1.3 點的凹凸性
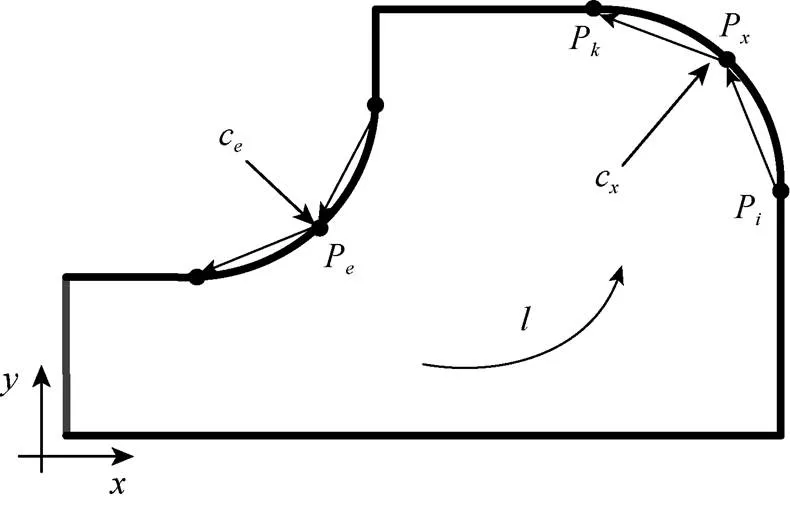
圖2 點與弧的凹凸性
1.4 弧的凹凸性
對于環上某一圓弧c,c上存在一點P,若P為凸點,稱該c為凸弧,記為c,若P為凹點,稱該c為凹弧,記為c,如圖2所示。
1.5 面間最短距離與面間最短距離集合
對于邊集E?L,其他邊到E的最小距離稱為槽腔F在F處的面間最短距離,記為d,其參數和表示為
d(e,e,) (5)
其中,e和e分別為形成面間最短距離的2條邊,且e∈E,e∈L;為最短距離的值。
F一般包含多個側面,考慮到此種情況,定義面間最短距離集合為

2 特征面之間最短距離計算
2.1 面面間距離計算轉化為線線間距離計算
側壁面根據其結構特點可以分為不含開閉角和內陷的側壁面(一般側壁面)、開角側壁面、閉角側壁面、內陷以及開閉角混合側壁面,其示意圖、頂邊集與底邊集如圖3所示。

根據面間最短距離的定義和圖3,一般側壁面和開角側壁面可用底邊集E來表示其位置,閉角側壁面和內陷面可用頂邊集E來表示其位置,開閉角混合側壁面需同時用底邊集E和頂邊集E來表示其位置。因此根據側壁面F的類型需要對L中相應的邊集E進行修正。
2.2 線線之間距離計算
由于樣條曲線的距離計算復雜,為了簡化算法,將L中所有非圓弧曲線均按照離散精度離散成直線鏈形式。離散精度太小會降低算法效率,太大會降低精度。為了保證離散后的直線鏈在一定程度上保持離散前的形狀,且與其他曲線的相對位置關系保持不變,的取值范圍為
其中,min,min分別為被離散曲線的最小曲率半徑和最小曲線長度。 由上文可知獲F面間最短距離dmin的前提條件是必須要計算獲得所有的最短距離d,而由d的定義可知,其距離計算歸根到底是線與線之間的距離計算。將L中所有非圓弧曲線均按照精度要求離散成直線鏈形式。因此,根據兩邊幾何類型的不同分為以下3類:①直線段與直線段之間的距離計算;②直線段與圓弧之間的距離計算;③圓弧與圓弧之間的距離計算。3種線線距離計算算法應用到如下幾種常用算法:點與點間距離計算、點與直線間距離計算、點是否在直線段上、點是否在圓弧上、直線段與直線段夾角計算。現利用上述算法分別描述線線之間距離的計算方法。 2.2.1 直線段與直線段之間的距離計算 如圖4(a)所示,直線段與直線段之間的距離計算可以根據2條直線段的相對位置關系不同分為2類:從e的始末點向e做垂線段,垂足點分別為點P和點P,從e的始末點向e做垂線段,垂足點為分別為P和P,若P,P,P,P中有一點位于直線段上,則e與e之間的距離必然為某端點所在的垂線段距離;反之,若P,P,P,P均不在e與e上,此時e與e之間的距離必然位于2個端點之間。 圖4 線線之間距離計算 2.2.2 直線段與圓弧之間的距離計算 如圖4(b)所示,直線段與圓弧之間的距離計算也可根據圓心到直線段上的垂足位置分為2種情況:圓弧e圓心到直線e的垂足點在e上,則垂線段的長度-即為所求距離;反之,若垂足不在e上,則圓心與e端點的距離-即為所求距離。 2.2.3 圓弧與圓弧之間的距離計算 如圖4(c)所示,圓弧與圓弧之間的距離計算只有一種情形。e所在圓心為1,半徑為1,e所在圓心為2,半徑為2,其圓心距為,則2個圓弧之間的距離=-1-2。 圖5 最短距離分析 準則1.對于給定邊集E,若不存在F∈F,使得(F)=E,則無需計算E和其他邊集之間的距離。 準則2.對于待求距離的2條邊e和e,若其屬于同一邊集,則無需計算e與e之間的距離。 準則3.給定槽腔F,相鄰側面之間的距離勿需計算。 準則4.對于任意待求距離的2條邊e和e,1代表e環在e其始點處正向矢量,2代表由e始點到e始點直線矢量。定義向量(,,),令=1×2,若滿足≤0,則無需計算e與e之間的距離。 準則5.對于任意待求距離的2條直邊e與e,若滿足e⊥e,則e與e之間的距離無需計算。 準則6.給定任意環,e與e表示上待求距離的2條直邊,1與2分別代表環在e與e始點處正向矢量,若1?2>0,則無需計算e與e之間的距離。 準則7.給定任意環,沿其正方向,若環上存在凸弧,則無需計算凸弧與該環上其他各邊的距離,將凸弧本身的直徑作為最短距離。 準則8.給定任意環,若存在連續3條邊e1,e,e1,其中,e滿足以下2個條件之一:①e的起點與終點凹凸性相反;②e為凸弧,則e1與e1之間的距離無需計算。 準則9.對于任意待求距離的一條凹弧邊c和一條邊e,和為c的2個端點,為c的圓心,和為e的2個端點,連接圓心和端點,交c于點,連接圓心和端點,交c于點,若點與點均不在圓弧c上,則c與e間的距離無需計算。 準則10.對于任意待求距離的2條邊e和e,點P與P分別表示e的起點與終點,點P與P分別代表e的起點與終點,則分別連接PP成直線1,連接PP成直線2,連接PP成直線3,連接PP成直線4。若1,2,3,4與除了e和e外的任意一條邊存在交點,則無需計算e與e之間的距離。 飛機結構件槽腔內面間最短距離計算的基本流程如圖6所示,具體步驟如下: 步驟1.對l與L進行預處理,包括邊集擴充和曲線離散; 步驟2.沿著各環正方向分別計算環上各點與圓弧的凹凸性; 圖6 槽腔特征面之間最短距離計算流程 根據上述算法在CATIA V5為平臺下進行程序開發,并已集成到“飛機結構件三維設計模型質量檢測系統”中。實例測試零件均為飛機大型結構件,包含各種不同槽腔,具有典型性和代表性。如圖7(a)所示,槽腔側面包含閉角面并且含有內陷,該實例測試在Windows 10系統上進行,電腦配置為Intel(R) Core(TM)i7-7500U CPU@ 2.70 GHz, 8.0 GB RAM,本文算法運行時間小于1 s,求得的最短距離如圖7(b)所示,圖中高亮紅色的2個面即為形成面間最短距離的面,該距離min=7.611 mm,與CATIA測量工具測得的數據一致,因此本文算法是有效的。 圖7 算法實例 為滿足自動數控編程系統對CAD模型質量的要求,提出飛機結構件槽腔內面間最短距離計算算法。首先,對槽腔側面的幾何特點進行分析,通過投影的方法將槽腔內面面之間的距離計算轉換成為線線之間的距離計算;然后根據槽腔特征本身的幾何屬性,制定一系列快速判定規則判斷距離的有效性,以減少不必要的求交與距離計算;最后以某飛機結構件模型為例,驗證了該算法的可行性和有效性。 [1] 范玉青. 航空宇航制造工程[M]. 重慶: 重慶出版社, 2001: 176-177. FAN Y Q. Aerospace manufacturing engineering[M]. Chongqing: Chongqing Press, 2001: 176-177 (in Chinese). [2] 于方方, 鄭國磊, 陳樹林, 等. 飛機整體壁板智能數控編程系統[J]. 航空制造技術, 2008(23): 83-88. YU F F, ZHENF G L, CHEN S L, et al. Intelligent NC programming system of aircraft integral panel[J]. Aeronautical Manufacturing Technology, 2008(23): 83-88 (in Chinese). [3] YU F F, DU B R, REN W J, et al. Slicing recongnition of aircraft integra panel generalized pocket[J]. Chinese Journal of Aeronautics, 2008(21): 585-592. [4] 趙丹, 陳樹林, 王碧玲, 等. 飛機結構件快速數控加工編程系統[J]. 航空制造技術, 2014(6): 73-77. ZHAO D, CHEN S L, WANG B L, et al. Rapid NC programming system for aircraft structure[J]. Aeronautical Manufacturing Technology, 2014(6): 73-77 (in Chinese). [5] 李桂東, 周來水, 安魯陵, 等. 復雜曲面零件可加工性分析的多屬性評價算法研究[J]. 中國機械工程, 2009(3): 315-319. LI G D, ZHOU L S, AN L L, et al. An approach to multi-attribute evaluation in machinability analysis for complicated surface parts[J]. China Mechanical Engineering, 2009 (3): 315-319 (in Chinese). [6] MYUNG S, HAN S. Knowledge-based parametric design of mechanical products based on configuration design method[J]. Expert Systems with Applications, 2001, 21(2): 99-107. [7] 王凱, 許建新. 飛機結構件三維模型工藝性優化技術研究[J]. 機械設計與制造, 2015(8): 178-185. WANG K, XU J X. Research on the technology of manufacturability optimization for aircraft structural components 3D model[J]. Machinery Design & Manufacture, 2015(8): 178-185(in Chinese). [8] 鄧高見. 機械產品CAD數據質量檢測實現技術研究[D]. 北京: 機械科學研究總院, 2008. DENG G J. Technology research on CAD data quality measure on mechanical product[D]. Beijing: China Academy of Mechanical Science and Technology, 2008 (in Chinese). [9] 張聰聰, 張樹生, 黃瑞, 等. 飛機結構件三維CAD模型缺陷識別方法[J]. 計算機集成制造系統, 2014, 20(9): 2099-2106. ZHANG C C, ZHANG S S, HUANG R, et al. Detecting defects method of 3D aircraft-structure model[J]. Computer Integrated Manufacturing systems, 2014, 20(9): 2099-2106 (in Chinese). [10] LAI W, FADDIS T, SOREM R. Incremental algorithms for finding the offset distance and minimum passage width in a pocket machining toolpath using the voronoi technique[J]. Journal of Materials Processing Technology, 2000, 100(1): 30-35 [11] VEERAMANI D, GAU Y S. Selection of an optimal set of cutting-tool sizes for 2? D pocket machining[J]. Computer-Aided Design, 1997, 29(12): 869-877. [12] 于芳芳, 鄭國磊, 饒有福, 等. 基于幾何特性的槽加工刀具選取算法[J]. 計算機輔助設計與圖形學學報, 2010, 22(11): 1984-4989. YU F F, ZHENG G L, RAO Y F, e al. Algorithms for selecting optimal cutters in pocket machining based on geometric characteristics[J]. Journal of Computer-Aided Design and Computer Graphics, 2010, 22(11): 1984-4989 (in Chinese). [13] 張石磊, 李迎光, 劉長青, 等. 基于環分析的飛機結構件槽特征腹板精加工區域自動創建方法[J]. 中國機械工程, 2013(24): 1728-1733. ZHANG S L, LI Y G, LIU C Q, et al. Loop- analysis-based automatic creation method for bottom finish machining region of pocket feature in aircraft sructural parts[J]. China Mechanical Engineering, 2013(24): 1728-1733 (in Chinese). Algorithm for calculating the shortest distance between the inner surfaces of the pocket of an aircraft structure HU Bao-ying1, ZHANG Tian-yang2, ZHENG Guo-lei3, ZHOU Min4 (1. Shenyang Aircraft Industry (Group) Corporation Limited, Shenyang Liaoning 110034, China; 2. China Aerospace Academy of Systems Science and Engineering, Beijing 100048, China; 3. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China; 4. College of Engineering, China Agricultural University, Beijing 100083, China) In the development process of the automatic programming system for computer numerical control (CNC) machining of aircraft structural parts, the process defects of the part feature, especially the shortest distance between the inner surfaces of the pockets being too small, was likely to complicate the processing of parts, incur high cost, or even render the processing impossible. At present, this model problem was mainly inspected manually, which was inefficient and error-prone. For the pockets of aircraft structural parts with complex shapes and such complex features as open and closed angles and indentations, it was difficult to determine the shortest distance between side walls. Based on the extraction of feature geometric parameters, the calculation of the shortest distance between side walls was converted to the computation of the shortest distance between lines. The validity rules of the distance calculation between lines were presented to simplify the calculation according to geometric features of the pocket’s characteristics, and the shortest distance between inner wall surfaces of pocket features was obtained. Finally, an aircraft structure model is taken as an example to verify the feasibility and effectiveness of the algorithm. shortest distance; processing property; computer numerical control machining automatic programming; aircraft structure; pocket TP 391 10.11996/JG.j.2095-302X.2020060987 A 2095-302X(2020)06-0987-06 2020-04-13; 2020-08-14 13 April,2020; 14 August,2020 胡寶瑩(1963-),男,遼寧沈陽人,高級工程師,學士。主要研究方向為計算機輔助設計/制造技術、航空制造技術等。 E-mail:sachby@163.com HU Bao-ying (1963-), male, senior engineer, bachelor. His main research interests cover CAM and aviation manufacturing technology. E-mail:sachby@163.com 周 敏(1985-),女,四川成都人,副教授,博士,碩士生導師。主要研究方向為計算機輔助設計/制造技術、增材制造。 E-mail:zhoumin2016@cau.edu.cn ZHOU Min (1985-), female, associate professor, Ph.D. Her main research interests cover CAD/CAM and additive manufacturing. E-mail:zhoumin2016@cau.edu.cn
2.3 距離有效性判斷

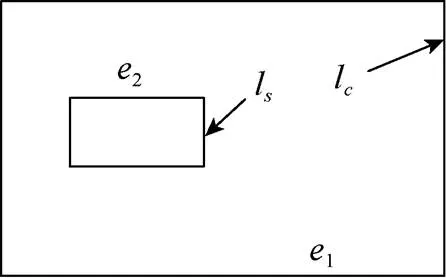
3 算法與實例






4 結 論

