月面著陸器INS/CNS深組合導航方法

孫洪馳，穆榮軍，李云天，崔乃剛

(哈爾濱工業大學航天工程系，哈爾濱 150001)

0 引 言

在月面著陸器下降過程中，需要快速調整姿態，要求導航系統具備高實時性、高精度和高可靠性[1-2]。當前深空探測任務中姿態精度最高的導航方式為天文導航，其姿態精度可達角秒級[3-5]。為提高導航系統的可靠性，月面著陸器通常都攜帶慣導與星敏感器，采用慣性/天文組合導航方式進行導航解算[6-7]。慣性/天文組合導航系統一般可分為松組合和緊組合兩種模式。松組合模式下慣導和星敏感器各自獨立地進行導航解算，然后將導航誤差作為觀測量進行組合[8]；緊組合模式下星敏感器不再進行獨立解算，而是作為測量星點矢量的傳感器使用，根據星點矢量誤差構建量測方程[9]。無論是松組合模式還是緊組合模式，星敏感器均需要采用星圖識別算法進行導航星的識別，這一過程往往是天文導航所有流程中耗時最多的環節[10-11]。

針對上述問題本文提出一種慣性/天文深組合模型，能在不進行星圖識別的前提下實現導航解算，有助于提高天文導航算法的計算效率，降低系統的功耗，減少對硬件資源的占用。同時在導航星數目不足3顆時仍可正常工作，可有效提高導航系統的實時性與可靠性。

1 月面著陸器運動學模型

月面著陸器運動學模型包括姿態微分方程、速度微分方程和位置微分方程。月面著陸器姿態采用四元數進行描述，姿態微分方程可以表示為

(1)

(2)

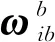
對于月面著陸器，在固連系下的速度ve為

(3)

將速度ve轉到導航系中，得

(4)

進一步整理，可得

(5)

(6)

式中:fb為體系下的比力；gn為導航系下的月球重力加速度。

記p=[L,λ,h]T，月面著陸器位置微分方程為

(7)

綜上所述，式(1)、式(6)和式(7)共同組成了月面著陸器運動學模型。

2 星敏感器測量模型與慣性/天文松、緊組合模型

2.1 星敏感器測量模型

在星敏感器中，圖像是以像素的形式進行采集和存儲的，為了能建立起星點矢量與像素坐標之間的關系，引入視覺導航領域常用的內參數矩陣構建星敏感器的測量模型。假設某導航星sk在星敏感器坐標系下的方向矢量為lsk=[X,Y,Z]T，則其在像平面中的坐標為

(8)

式中:f為星敏感器焦距。將星點坐標轉換到像素坐標系下，得

(9)

式中:α和β描述了像平面坐標和像素坐標的縮放關系，物理含義是單位長度內的像素數目；cx和cy描述了像平面坐標和像素坐標的平移關系，單位為像素數；fx=αf,fy=βf，作用是簡化模型。將式(9)寫成矩陣形式，得

(10)

式中:A即為星敏感器的內參數矩陣，且各項參數出廠后是固定不變的。l′sk為lsk的歸一化矢量。

2.2 慣性/天文松組合模型

慣性/天文松組合是最常見的組合方式，該模式下慣導與星敏感器各自獨立工作，利用二者輸出的姿態之差構建觀測量。狀態方程選取捷聯慣導系統的誤差傳播方程，具體推導過程參照文獻[12]。

姿態誤差傳播方程為

(11)

速度誤差傳播方程為

(12)

位置誤差傳播方程為

(13)

(14)

(15)

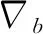
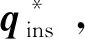
(16)

記δq=[δq0, (δqv)T]T，δq0和δqv代表δq的標量部分和矢量部分。當φ為小量時，令φ=|φ|，有

(17)

由式(17)可以得到觀測量為φ=2δqv。

選取姿態失準角、速度誤差、位置誤差、三軸陀螺儀零偏和加速度計零偏作為狀態變量，松組合模式下狀態量、狀態方程和量測方程為

(18)

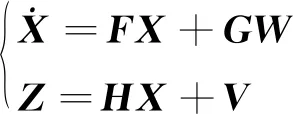
(19)

式中:W為陀螺角速度測量白噪聲和加速度計比力測量白噪聲；V為星敏感器測量白噪聲；F陣各元素取值參照式(11)致式(15)，G陣和H陣各元素取值如下

(20)

2.3 慣性/天文緊組合模型

慣性/天文緊組合模型以星點矢量誤差為觀測量，該模式下星敏感器不進行姿態解算。緊組合狀態方程仍為慣導系統的誤差傳播方程，僅觀測方程有所不同。在緊組合模型中，星敏感器測量到的星點矢量ls可以表示為

(21)

式中:ln為該星點矢量在導航系下的投影，φ為導航系的姿態失準角。

(22)

(23)

當視場中存在N顆導航星時，觀測方程可以表示為

(24)

觀測矩陣H陣各元素取值如下

(25)

3 慣性/天文深組合模型

慣性/天文深組合模型根據慣導輸出的姿態，預測此姿態下理論上星敏感器應觀測到的星圖(記為預測星圖)，然后利用預測星圖和實測星圖的灰度誤差進行失準角的估計，從而在像素層面構建新的觀測模型而非對單個星點進行處理，故深組合時不需要星圖識別。

3.1 基于李群李代數理論的灰度誤差函數

群是一種集合加一種運算組成的代數結構，李群指具有連續性質的群。構建灰度誤差函數需涉及到其中一個特殊的李群—特殊正交群SO(3)，是由姿態陣C構成的，其數學定義為

SO(3)={C∈R3×3|CCT=I,det(C)=1}

(26)

對于每一個C，都有對應的李代數，SO(3)的李代數so(3)定義為

so(3)={(φc×)∈R3×3|φc∈R3}

(27)

so(3)反映了SO(3)的導數性質，對姿態陣C求微分，有

(28)

式中:φc的物理意義是姿態陣C對應的等效旋轉矢量，式(28)為關于C的微分方程，求解后得到

C=exp(φc×)

(29)

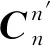
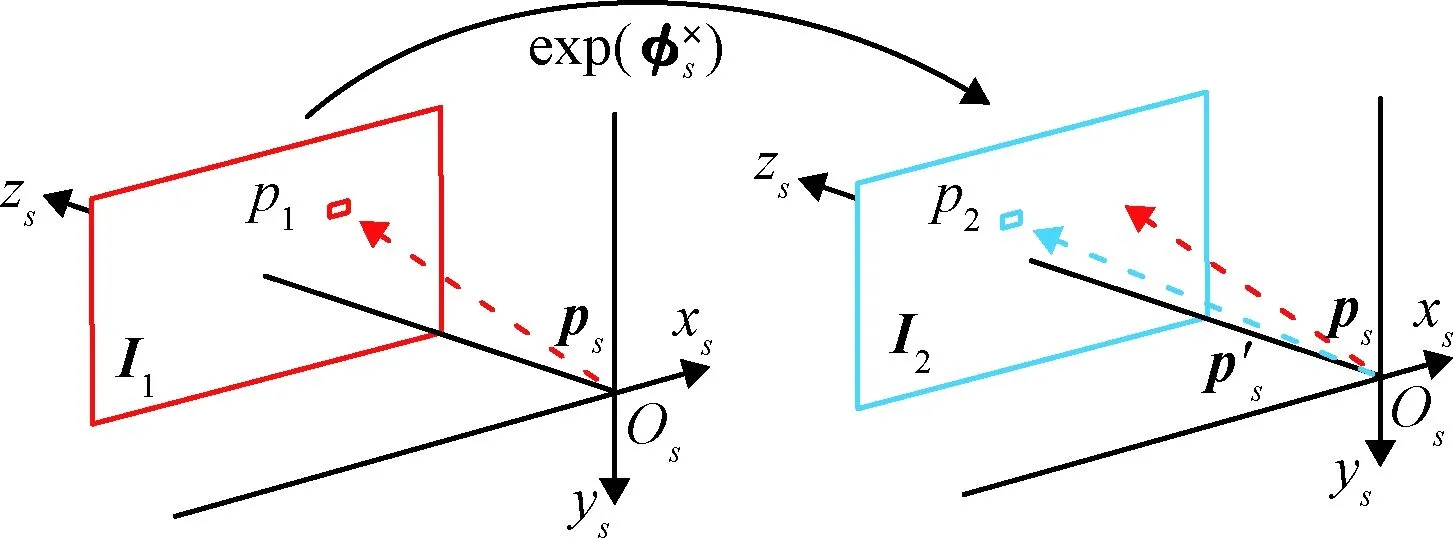
圖1 灰度誤差函數構建過程

如圖1所示，I1為星敏感器拍攝星圖，I2為慣導預測星圖，設p1為I1中第i個像素點，滿足

p1=Aps

(30)

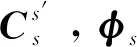
(31)

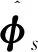
(32)

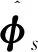
(33)

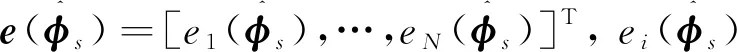
ps和p′s可視為同一矢量的真值及慣導預測值，pn為該矢量在導航系下的投影，滿足

(34)

由式(34)即可得到φ與φs的關系式為

(35)

3.2 基于阻尼牛頓法的姿態優化算法

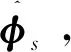
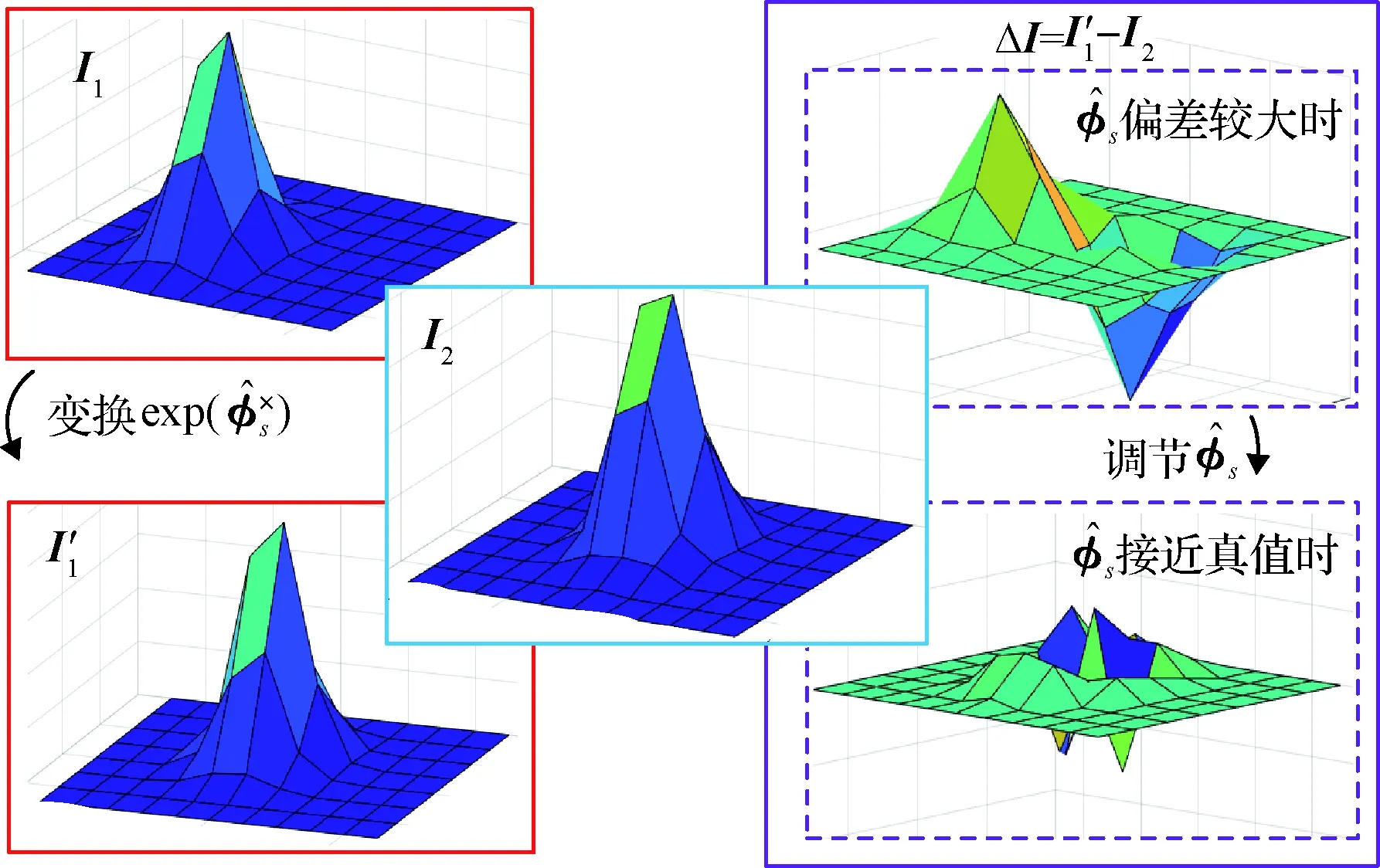
圖2 深組合模型基本原理

根據灰度不變假設，式(32)可進一步寫為

(36)

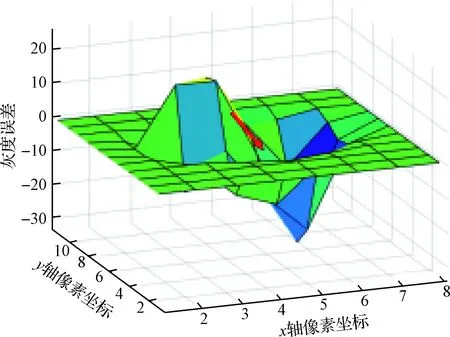
圖3 某星點窗口內灰度誤差優化方向

(37)

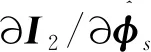
(38)

接下來分別計算這3項偏導數，?I2/??為I2在?處的像素梯度，記?像素坐標為?=[ua,ub]T，則像素梯度為

(39)

記ρ=[Xρ,Yρ,Zρ]T，利用式(10)，可以求得??/?ρ的具體形式為

(40)

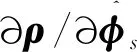
(41)

根據BCH公式，有

(42)

(43)

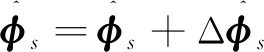
3.3 慣性/天文深組合濾波模型

為提高算法的計算效率，可針對月面環境特征對狀態方程做進一步簡化。例如，月球自轉速度很小，且月面著陸器下降過程時間較短，所引起的導航系旋轉也很微弱，月面重力較弱，其誤差項δgn對速度誤差的影響也是小量。忽略狀態方程式(11)-式(15)中的小量后，可得簡化后的狀態方程為

(44)

量測方程與式(19)一致。狀態與量測方程都是線性模型，離散化后可采用標準卡爾曼濾波進行狀態估計。

4 仿真校驗

4.1 算法魯棒性驗證

利用慣導姿態預測星敏光軸指向，估算的星點和實際觀測星點不一定完全匹配，慣導預測星圖會出現缺星和多星的現象。但根據式(33)可知，本文所提出的深組合算法，其優化對象為所有導航星堆疊而成的全局灰度誤差，優化結果為最小二乘意義下的最優解，故理論上個別星點的不匹配不會對最終結果造成太大影響，接下來通過仿真進行驗證。

采用SAO星表數據進行仿真驗證，歲差、章動采用IAU1980模型進行補償，光行差只考慮一階修正項，極移修正量由國際地球自轉服務(International earth rotation service，IERS)提供。星圖不確定度按低(不確定度：17%)、中(不確定度：50%)、高(不確定度：70%)三種情況進行仿真驗證。

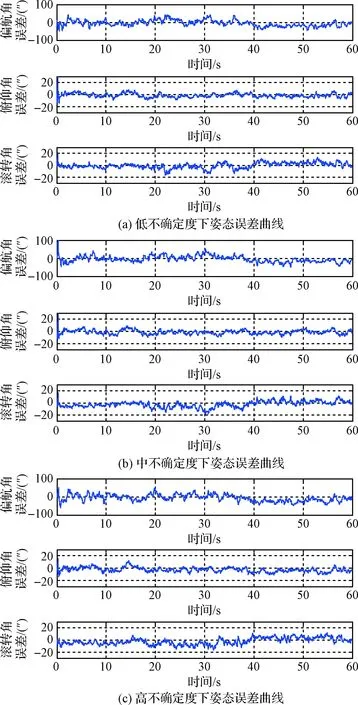
圖4 低、中、高三種不確定度下姿態誤差曲線

從圖4(c)中可以看出，即使在高不確定度下，慣導僅正確預測30%的導航星，深組合算法依然收斂，三種工況僅精度略有不同。這說明深組合算法具有較強的魯棒性，慣導僅需要正確預測到其中的幾顆亮星即可進行導航解算。

(45)

式(45)表明，對全部導航星做優化等價于只優化正確匹配的星點，不匹配的星點由于灰度誤差為常值，不影響優化結果。

4.2 三種組合方式對比仿真

本文所提出的方法主要針對月面著陸器姿態調整段進行設計，仿真軌跡設置為姿態調整段一條持續時間60 s的軌跡。著陸過程中著陸器姿態變化及星敏感器視場內的星圖變化如圖5所示。

采用阻尼牛頓法一般迭代3～4次即可使姿態達到收斂。取第1、4次迭代優化結果，對比其圖像灰度誤差，對比結果如圖6所示。

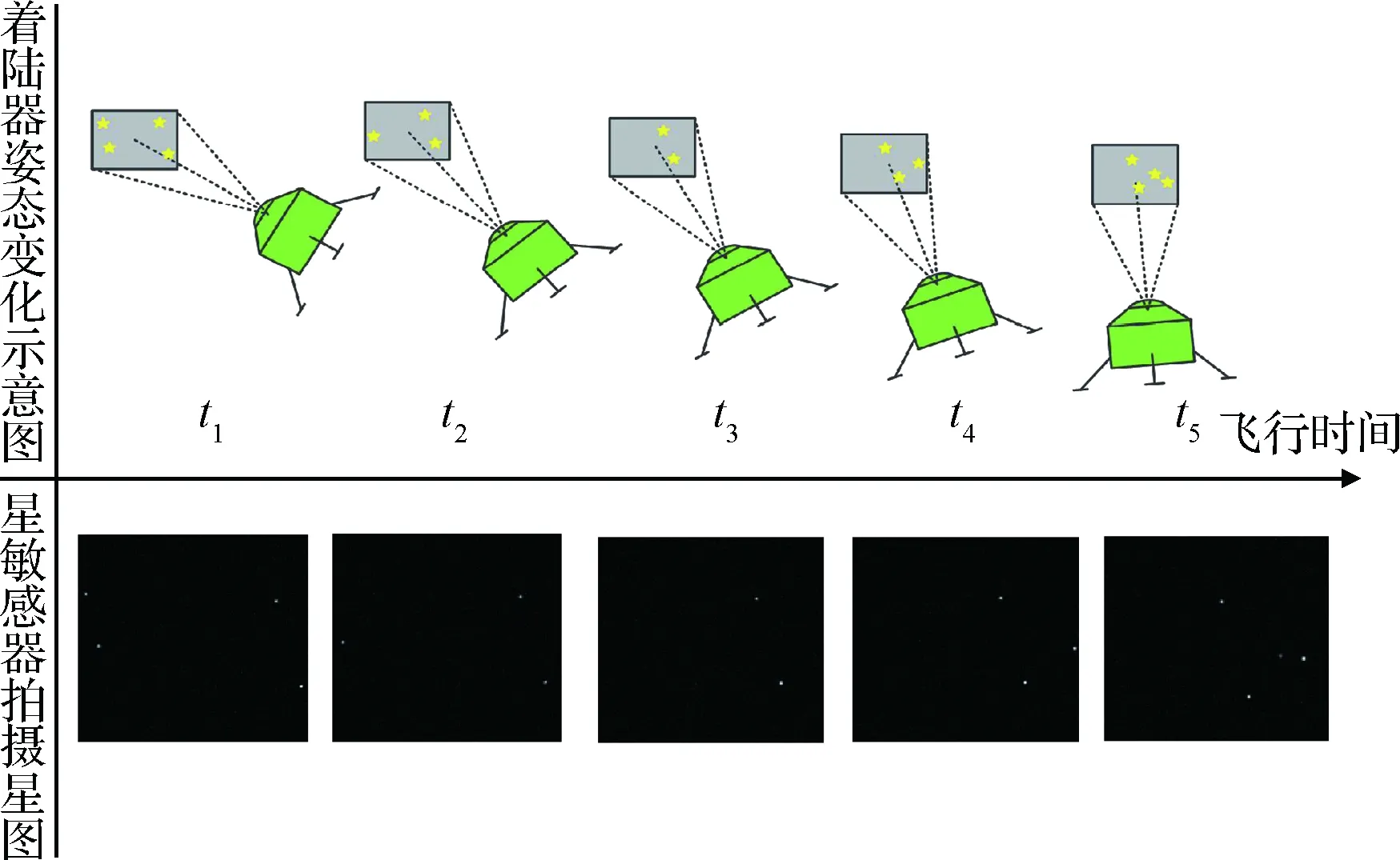
圖5 仿真工況設計

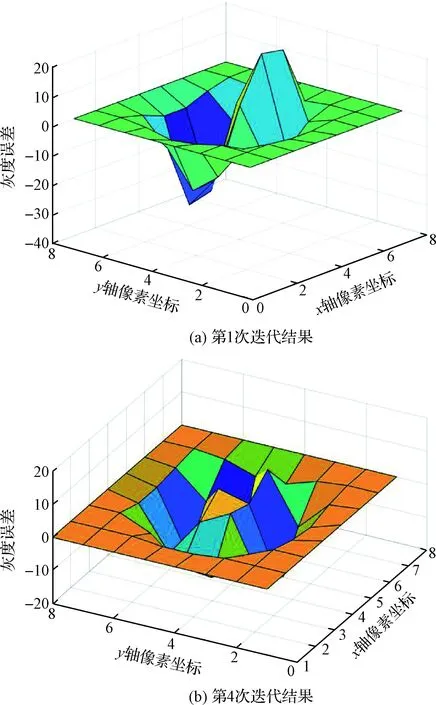
圖6 某星點窗口內圖像灰度誤差迭代結果

接下來對比慣性/天文松、緊、深三種組合模式下的組合導航精度和算法計算耗時。緊組合模式只進行星圖識別不進行QUST解算，故算法耗時應少于松組合。深組合模式則是采用圖像梯度優化算法獲得姿態，一般迭代4次算法已經收斂，平均每顆星占據3×3即9個像素點，故平均每顆星需要優化算法迭代計算36次；而緊組合的星圖識別算法，采用星表分割后(極限星等+6Mv)平均每個子星表依舊含有196顆導航星，角距搜索空間大小為196×196/2=19208，即平均每顆星需要進行的搜索次數為19208次，顯然這一過程的計算量要大于深組合的優化算法。三種組合方式的解算精度和算法耗時統計仿真結果如圖7和圖8所示。

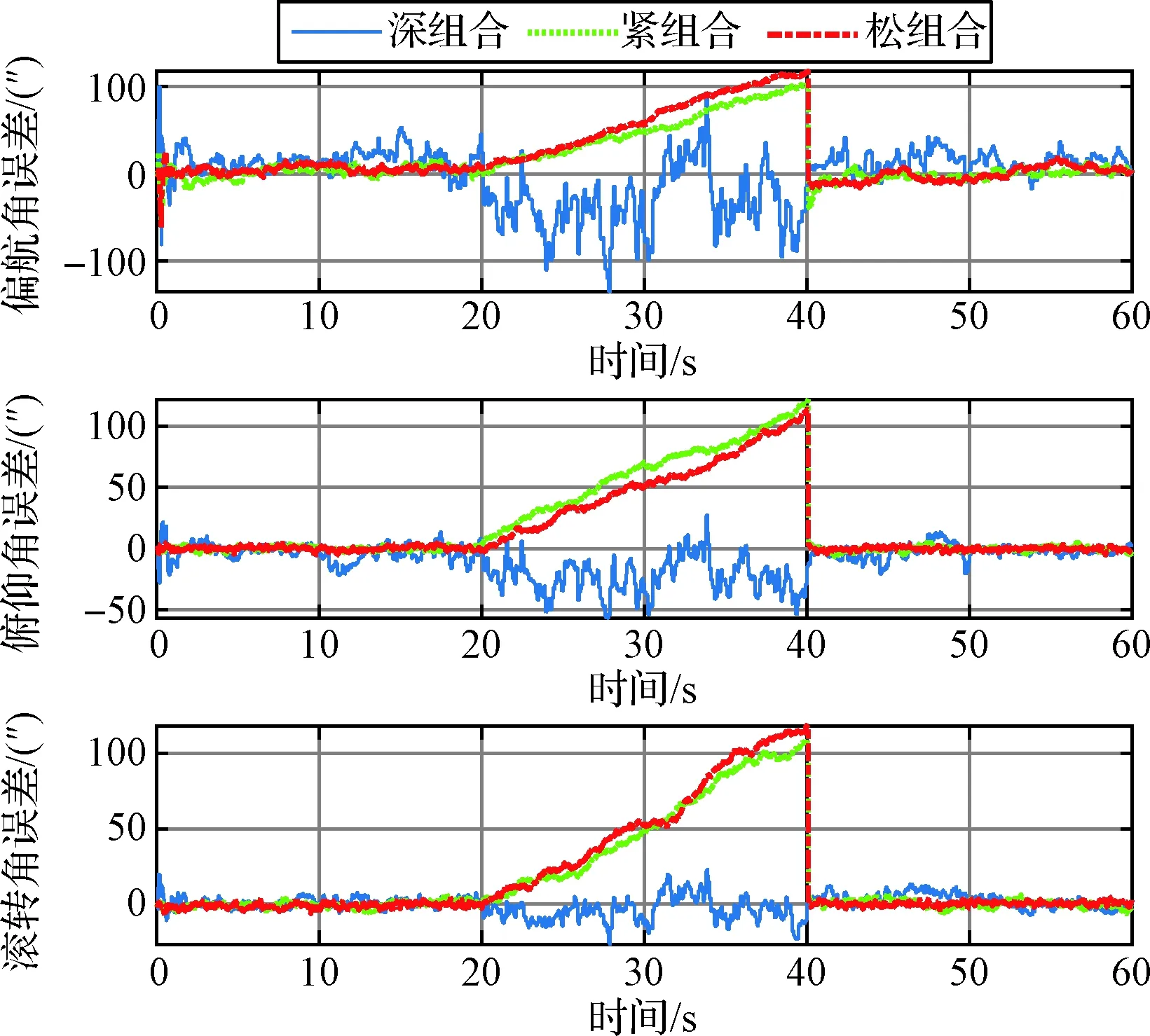
圖7 松、緊、深組合導航模式精度對比

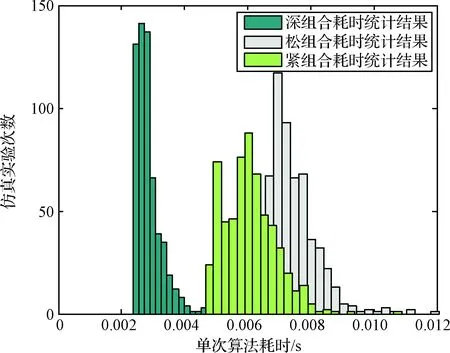
圖8 松、緊、深組合導航模式計算耗時對比

分析圖中不同階段的三種導航模式精度曲線和計算耗時統計直方圖，可以得到以下分析結果：

1) 0～20 s內導航星充足(≥3顆)，松、緊、深三種組合導航模式的姿態精度基本處于同一量級；

2) 20～40 s內視場中可見導航星降為2顆，星圖識別算法失效，松、緊組合模式導航結果開始發散，深組合模式依舊可以進行導航解算；

3) 40～60 s時視場內可見導航星數目恢復到≥3顆，此時松、緊組合導航模式迅速收斂，三種導航模式的姿態精度基本處于同一量級；

4) 俯仰、滾轉軸姿態精度整體上優于偏航軸，這是因為偏航軸與星敏感器光軸重合，星敏感器光軸方向的姿態精度較其余兩軸差一個量級；

5) 經統計，松、緊、深三種組合模式的單次計算耗時均值分別為0.0074 s、0.0061 s、0.0029 s。深組合模式計算耗時最低。

5 結 論

本文針對月面著陸器設計了一種慣性/天文深組合導航方法。仿真結果表明，在導航星數目充足的情況下，松、緊、深三種導航方式姿態精度處于同一量級；在導航星數目不足時，松、緊組合方式無法實現導航星的識別，算法開始發散，而深組合模式依然可以正常工作；在計算耗時方面，深組合模式相較于緊組合時間縮減50%、相較于松組合時間縮減60%。深組合模式計算耗時短，有利于提高月面著陸器導航實時性，降低對硬件資源的占用，同時可保證在星敏感器視場內星點數目不足時，導航結果不發散。將其應用于月面著陸器等實時性需求較高的背景中，可以有效提升導航系統的快速響應能力并節約系統功耗，為未來月面著陸器導航系統設計提供理論參考。