基于截斷核范數正則化的協方差矩陣估計
李 明,孫國皓,何子述
(1. 電子科技大學信息與通信工程學院,四川成都 611731;2. 四川大學空天科學與工程學院,四川成都 610065)
0 引言
機載雷達為應對地面慢速運動目標檢測的調整,通常采用空時自適應處理(Space Time Adaptive Processing,STAP)作為重要手段[1],而目標距離環(Cell Under Test,CUT)雜波協方差矩陣(Clutter Covariance Matrix,CCM)的估計是機載STAP的關鍵步驟[2]。在CCM的估計過程中,要求選擇無目標的訓練樣本,且與CUT的雜波信號保持獨立同分布。此外,所提供訓練樣本數量至少要達到空時維度的兩倍,以確保高輸出信雜噪比(Signal-Clutter-Noise Ratio,SCNR)。而實際應用場景通常為非均勻雜波環境,尤其對于高維度應用,如多脈沖、大陣列,無法提供足夠的均勻訓練樣本。
為了利用有限樣本精確估計CCM,學者們提出了許多算法。降維算法[3]和降秩算法[4]可以有效降低用于CCM估計所需樣本數量。文獻[5]中的直接數據域STAP算法僅需利用目標距離環數據估計CCM,直接回避了訓練樣本不足的問題。然而,上述這些算法犧牲了系統自由度,會導致STAP性能降低。近年來,學者們根據雜波自身的稀疏性,提出了稀疏恢復(Sparse Recovery,SR)算法,該類算法可在空時域內獲得高分辨率。然而,對于絕大多數稀疏恢復算法,如正交匹配追蹤算法(Orthogonal Matching Pursuit,OMP)[6],建立信號模型需利用離散化字典,會導致網格點失配問題,從而嚴重影響算法性能[7]。為了解決網格點失配問題,文獻[8]提出的原子范數最小化(Atomic Norm Minimization,ANM)算法,通過利用CCM的塊Toeplitz結構特性支持多維范德蒙分解實現連續域信號建模,但是由于秩最小化問題為NP-hard問題,該算法采用核范數對矩陣的秩進行松弛,然而對于STAP處理時的CCM這類具有多維Toeplitz結構的矩陣,核范數松弛無法保證所估計協方差矩陣的低秩特性[9]。
基于上述分析,本文提出了一種基于截斷核范數正則化(Truncated Nuclear Norm Regularization,TNNR)的CCM估計算法,可有效解決非均勻雜波環境下(即有限樣本)的STAP處理問題。本文主要創新為利用TNNR確保所估計CCM的低秩特性,同時結合CCM的塊Toeplitz結構先驗信息。與常規秩最小化算法不同,如核范數松弛算法,其對所有奇異值的和求最小化處理,難以準確近似矩陣的秩,由于CCM的秩僅與非零奇異值有關,本文所采用的TNNR算法僅求解與矩陣的秩不相關的較小的奇異值的和,從而間接控制CCM的秩,確保低秩估計。同時,通過迭代求解思想,將TNNR優化問題轉換為凸優化問題實現求解。此外,結合機載雷達的信號模型特征,我們在CCM的估計過程中引入塊Toeplitz結構約束,由于塊Toeplitz矩陣可支持多維范德蒙分解,從而可確保CCM的估計建立在連續域模型上,可避免了常規稀疏恢復算法由于引入離散化字典導致的網格點失配問題。仿真實驗表明本文所提出的算法相比于其他同類算法具有更高估計精度,性能更加出色。
1 機載雷達STAP信號模型
假設機載雷達采用以半波長為間隔布陣的正側視均勻線陣(ULA),共有N個陣元,每個陣元在一個相干處理間隔內發射M個脈沖,脈沖重復頻率為fr。發射波長為λ,陣元間距d為λ/2。對于目標距離環(CUT)的接收信號x∈CNM可以表示為
x=s+c+n
(1)
式中,s表示運動目標回波信號,c表示雜波信號,n為噪聲向量。對于單個反射點的陣列響應,可以表示為空域導向矢量與時域導向矢量的Kronecker積形式。空域導向矢量和時域導向矢量可分別表示為ar(fr)∈CN,ad(fd)∈CM,fr和fd分別表示某個反射點歸一化的空間頻率和多普勒頻率。反射點的空時導向矢量可表示為空域導向矢量與時域導向矢量的Kronecker積,即ad,r=ad(fd)?ar(fr)。
由上述所得,目標信號可表示為
s=α0ad(fd0)?ar(fr0)∈CNM
(2)
式中,?表示Kronecker積,α0表示目標回波信號復幅度,fr0和fd0分別表示運動目標歸一化的空間頻率和多普勒頻率。
對于雜波信號,我們將所選定距離環劃分為Nc個雜波片,回波信號響應即可表示為這些雜波片回波信號的總和[10],即
(3)
式中,αi表示第i個雜波片的回波信號復幅度,fri和fdi分別表示第i個雜波片的歸一化的空間頻率和多普勒頻率。
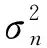
當機載雷達采用大規模陣列或使用多脈沖體制時,其CCM維度會很高,從而導致難以為CCM的估計提供充足的均勻樣本。因此,本文提出了一種基于TNNR的STAP算法,以確保機載雷達STAP處理在非均勻雜波環境下的性能。
2 基于TNNR的協方差矩陣估計
根據Brennan法則[11-12],利用Mr=?N+β(N-1)」個空時導向矢量即可表示接收信號中的雜波成分并可張成雜波子空間,即
(4)
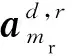
當存在多個不包含目標的均勻訓練樣本時,我們可以利用這些樣本的聯合稀疏性來提升CCM的估計準確度。假設這些樣本均具有相同的雜波子空間,則這K個訓練樣本的雜波信號矩陣可表示為
(5)
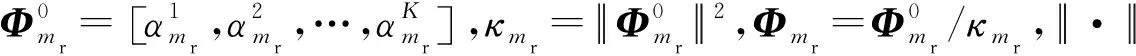
利用這K個訓練樣本,CCM可以表示為
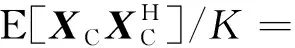
(6)
顯然XC可看作Mr個原子的線性組合[12],其中原子集合可表示為
AMMV={ad,r(f,Φ)|f∈[0,1)×[0,1),
Φ2=1}
(7)
式中,ad,r(f,Φ)[ad(fd)?ar(fr)]ΦT。然后,雜波信號矩陣XC的原子l0范數可表示為用AMMV中的原子表示該矩陣所需最少原子個數,
(8)
因此,通過以下的原子范數最小化算法即可提取訓練樣本信號矩陣X中的雜波成分:
s.t.X-Ξ2≤Kεn
(9)
式中,Ξ表示為XC的估計。然后我們利用調整參數可將優化問題改寫為以下形式:
(10)
式中,λ>0為調整參數。式(10)中的優化問題由于包含ΞAMMV,0,是NP-hard問題,無法直接求解。由文獻[12],ΞAMMV,0=rank(RC)=Mr,此外,RC具有塊Toeplitz矩陣,在優化求解中通過考慮先驗結構信息可以有效提高估計精度。同時為了將樣本雜波信號矩陣與RC,此處引入新的矩陣Z±0,即

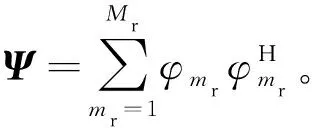
(12)
(13)
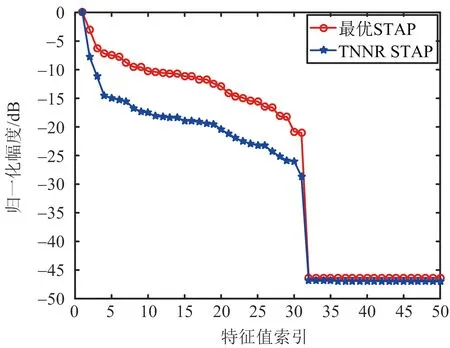
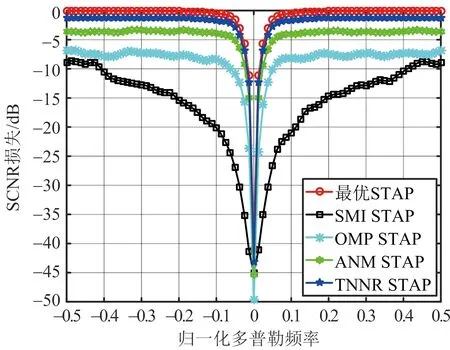
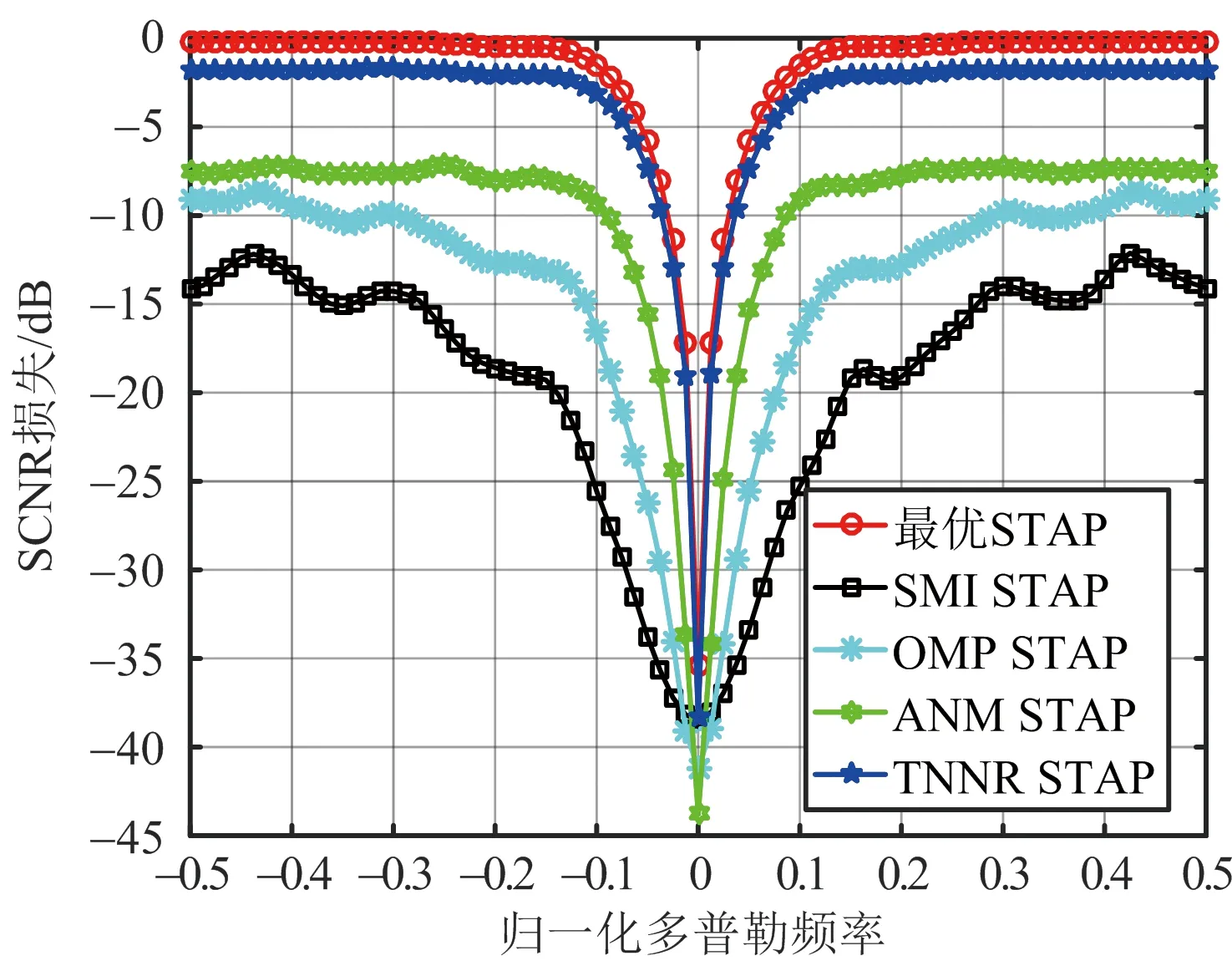
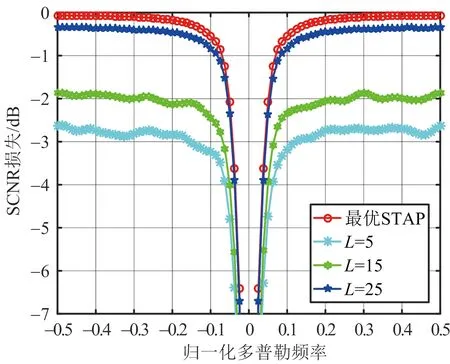
式中,T=[xl1,l2]∈C(2M-1)×(2N-1),-M (14) 然而,上述式(14)中的優化問題包含秩函數,仍然為NP-hard問題。現存優化算法無法直接求解秩最小化問題。通常,我們利用核范數對矩陣的秩進行松弛,以實現將非凸問題轉化為凸優化問題,如文獻[12]中ANM算法所采用的方法。但理論研究表明核范數,即矩陣奇異值的總和無法高度近似矩陣的秩[15-16],因為矩陣的秩僅與所有非零奇異值有關,但是核范數無差別對待所有奇異值,對總體進行求和,在實際應用中性能較差,無法高度近似矩陣的秩函數。 為了解決式(14)中的秩最小化問題,我們利用TNNR算法對矩陣Z的秩進行更加精確的近似。根據文獻[15],對于秩為r的矩陣B∈CNM×NM,其截斷核范數(Truncated Nuclear Norm,TNN)被定義為最小個NM-r個奇異值的和,即 (15) 其中,σi(B)表示矩陣B按遞減順序排列的第i個奇異值。 在使用TNNR時,由于涉及矩陣Z的秩,我們可以利用Brennan法則估計協方差矩陣RC的秩,然后根據rank(RC)=rank(Z)。與基于核范數的方法不同,本文所提出的基于TNNR的算法僅針對NM-Mr個最小奇異值進行處理,而由于矩陣的秩僅與較大的Mr個奇異值相關,因此通過求解中約束較小NM-Mr個奇異值的和近似為零,即可控制所得協方差矩陣的秩[15-16],從而更加精確的近似CCM的秩。因此,式(14)可重新整理為如下形式: (16) 其中τ>0,因為Zr是非凸的,我們仍然不能直接求解式(16)。我們引入一個新的矩陣A∈CNM,其滿足AAH=INM,其中INM是一個NM×NM的單位陣。 根據VonNeumann的跡的不等式可得 Tr(AZAH)=Tr(ZAHA)≤ (17) (18) 由上述推導可得 (19) 通過將式(19)與式(17)結合,可得 (20) 由于Z為半正定Hermitian矩陣,可用其特征值分解替代奇異值分解。假設Z的特征分解為Z=UΣUH,其中U=(u1,…,uNM)H∈CNM×NM,Σ∈CNM×NM為Z的特征值構成的對角矩陣,那么當 A=(u1,…,uMr)H (21) 則式(20)可取等號。然后我們可得如下結果: (22) 因此,Z的TNN可表示為 (23) 根據式(23),式(16)中的最小化問題可以被重新表達為如下形式: 我們可以通過迭代的方式解決上述優化問題。將文獻[12]中ANM算法的結果作為初始值,即Z0=ZANM。在進行第k次迭代時,我們固定Zk然后通過對其進行特征分解求得Ak,然后固定Ak更新Zk+1,即解決如下優化問題: 而上述優化問題為凸優化問題。通過上述迭代更新,當Zk+1-ZkF≤ε時,迭代過程停止,其中·F表示矩陣的Frobenius范數。我們得到最終的Z,從而可得RC。 關于矩陣Z的分解不是唯一[17],上述求解的RC僅能表征雜波子空間。為了準確獲得CCM,我們需要進行如下的校正操作。假設RC的特征分解為 RC=QΛQH (26) 式中,Q表示RC的特征向量矩陣,Λ表示對角矩陣,其對角線元素對應為RC的特征值。因此,RC可表示為[12] (27) 式中,diag(·)表示對角陣,Ξ(l)表示估計所得的第l個訓練樣本。 圖1顯示了基于TNNR的雜波協方差矩陣估計算法與理想協方差矩陣的特征譜。當β=1,根據Brennan法則可準確估計雜波秩,其雜波秩為31,圖中顯示,基于TNNR的雜波協方差矩陣估計算法的估計結果其特征譜在第31個特征值處有陡峭下降,與理想雜波協方差矩陣趨勢一致,即本文所提出的基于TNNR的雜波協方差矩陣估計算法可有效保證所估計矩陣的低秩特性。 圖1 雜波協方差矩陣的特征譜 圖2展示了當雜波脊斜率為整數(β=1)時,不同STAP算法的SCNR損失對比曲線圖。由圖中結果可以看出,本文所提出的基于TNNR的雜波協方差矩陣估計算法的STAP性能顯著優于OMP、ANM以及樣本矩陣求逆(Sample Matrix Inversion,SMI)算法,這是由于基于TNNR的雜波協方差矩陣估計算法不僅可以確保估計的雜波協方差矩陣的低秩特性,同時還結合了雜波協方差矩陣的塊Toeplitz結構先驗信息,有效提高了小樣本下的協方差矩陣估計精度,因此相比其他STAP算法性能更優。 圖2 SCNR損失對比曲線圖(β=1) 圖3和圖4顯示了當雜波脊斜率為非整數(β=0.79/2.31)時,不同STAP算法的SCNR損失對比曲線圖。當雜波脊斜率為非整數時,根據Brennan法則,無法準確估計雜波秩,但是本文提出的基于TNNR的雜波協方差矩陣估計算法的STAP性能仍然顯著優于OMP、ANM以及SMI算法。該實驗結果表明,即使在雜波秩信息不準確的情況下,基于TNNR的雜波協方差矩陣估計算法仍然具有出色的性能,優于OMP、ANM以及SMI算法。 圖5展示了基于TNNR的雜波協方差矩陣估計算法在不同訓練樣本數量下的SCNR損失對比曲線圖。由圖中結果可以看出,隨著訓練樣本數量的增加,本文所提出算法的STAP性能會明顯提升,當訓練樣本足夠多時(L=200<2NM),基于TNNR的STAP算法性能接近最優STAP性能,相差小于1 dB。 圖3 SCNR損失對比曲線圖(β=0.79) 圖4 SCNR損失對比曲線圖(β=2.31) 圖5 訓練樣本數量不同時的TNNR STAP的 SCNR損失對比曲線圖 本文提出了基于TNNR的CCM估計算法以確保機載雷達STAP在非均勻雜波環境下CCM估計的準確性。通過將CCM的低秩特性與塊Toeplitz結構相結合,新算法可以很好滿足訓練樣本不足情況下的應用場景。相比于核范數松弛算法,本文所采用的TNNR算法可以更加準確地近似矩陣的秩,從而有效確保所估計CCM的低秩特性。相比同類算法,本文所提出的CCM估計算法在非均勻雜波環境下的STAP估計性能更加出色。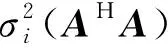
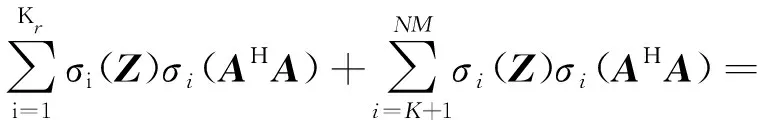
3 實驗和結果分析
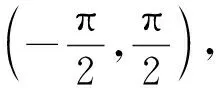

4 結束語

