隨機3種群時滯食物鏈系統的持久性和非持久性
李海紅,李海霞
(1.吉林建筑大學基礎科學部,吉林 長春 130118;2.長春光華學院商學院,吉林 長春 130031)
0 引言
生態系統不但與當時的因素有關,也與時滯效應有密切的聯系.為了更好地還原生態背景,人們將時滯引入種群動力學模型[1-2].
本文研究的3種群時滯食物鏈系統可表示為
(1)
系統(1)描述了后者捕食前者的3種群時滯食物鏈模型,這里假設中層和頂層捕食者擁有捕食能力的時間為τ[3],獵物成熟時間為τ,捕食者僅捕食成熟獵物.在系統(1)中引入隨機擾動,得到隨機時滯系統:
(2)
本文主要研究在白噪聲干擾下隨機時滯系統(2)的持久性和非持久性.
1 系統(2)的持久性
首先給出隨機系統在均值意義下持久性的定義[3].
定義1.1稱系統(2)在時間均值意義下是持久的,若有
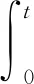
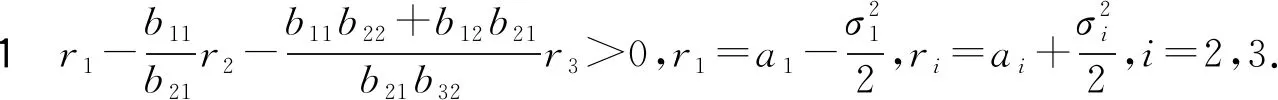
引入系統:
(3)
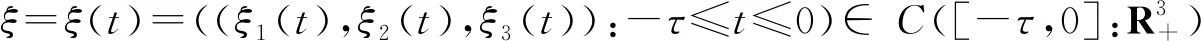
引理1.2若假設1成立,則系統(3)的解滿足如下結論:
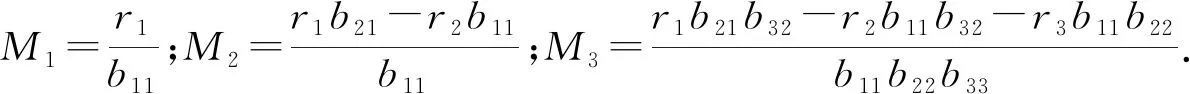
證明由文獻[5]和假設1得
(4)
應用伊藤公式,系統(3)的第2個式子可變形為
dlogΦ2(t)=(-r2+b21Φ1(t-τ)-b22Φ2(t))dt-σ2dB2(t).
進一步可得

(5)
注意到

則
(6)
由文獻[4]的引理1.3和假設1可得
dlogΦ3(t)=(-r3+b32Φ2(t-τ)-b33Φ3(t))dt-σ3dB3(t),
由帶擾動的非自治的Logistic方程解的形式[6],可得
x(t)≤Φ(t),
(7)
其中Φ(t)為隨機時滯微分方程(3)的解.
綜上,再由文獻[4]的引理1.2,下述結論顯然成立:
定理1.1若假設1成立,則系統(2)的解x(t,ξ)滿足
進一步有:
定理1.2若假設1成立,則系統(2)的解x(t,ξ)滿足
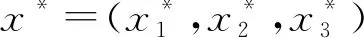
證明由系統(2)可得
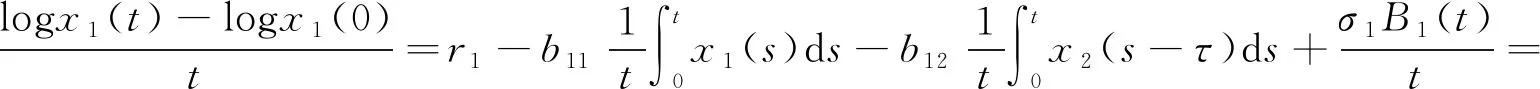
類似有
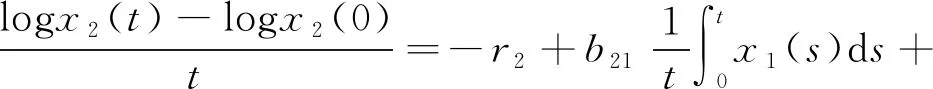
且

則
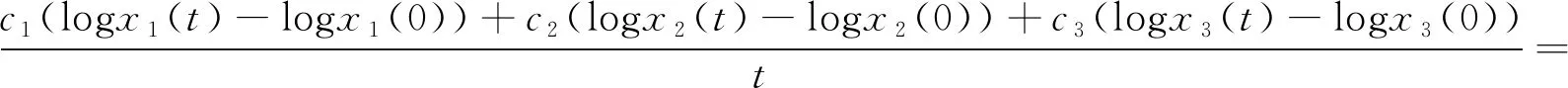
且由(7)式可知
(8)

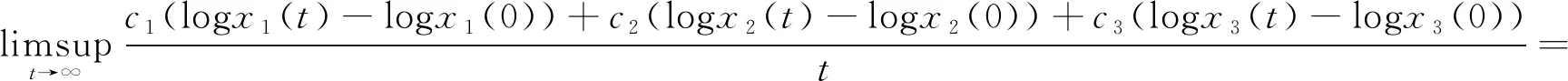
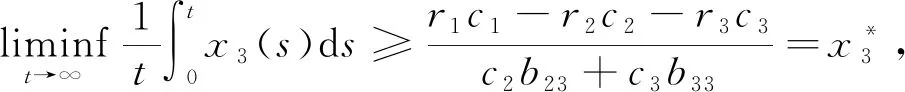
2 系統(2)的非持久性
分兩種情況分析隨機系統的非持久性.
情形1r1<0.
由伊藤公式,系統(3)的第一個方程可變形為
dlogΦ1(t)≤(r1-b11Φ1(t))dt-σ1dB1(t).
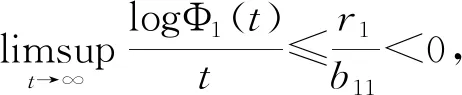
則
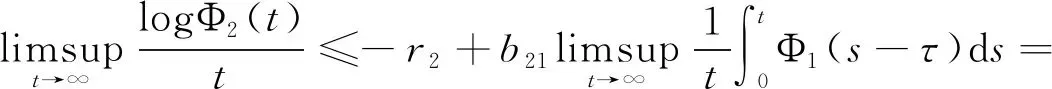
類似有:
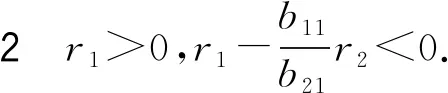
顯然,由情形1的證明過程可得
類似有
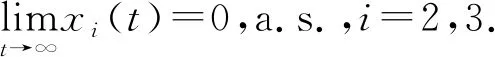
由上述討論可得如下結論:
定理2.1若假設1成立,x(t,ξ)是系統(2)的解,則有:
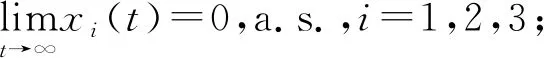
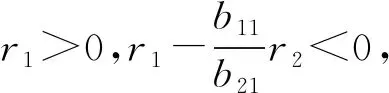
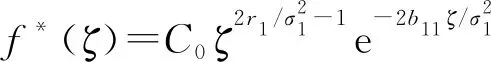
3 數值模擬
由Milstein方法,得到系統(2)的離散方程:
其中ε1,k,ε2,k,ε3,k是服從N(0,1)的高斯隨機變量.選取適當的參數,通過Matlab軟件,模擬計算下列實例:
(1) 確定性系統和隨機系統(2)的持久性.選取初始條件和系數為(x1(0),x2(0),x3(0))=(0.9,0.3,0.2),t∈[-τ,0],a1=0.7,a2=0.3,a3=0.1,b11=0.3,b12=0.2,b21=0.3,b22=0.5,b23=0.3,b32=0.4,b33=0.8,σ1=0.02,σ2=0.01,σ3=0.01.通過Matlab軟件計算,得到確定性系統和隨機系統(2)的持久性(圖1).圖1表明,當白噪聲很小時,選取恰當的參數使其滿足定理1.2條件,則系統(2)的解將在均值意義下持久.
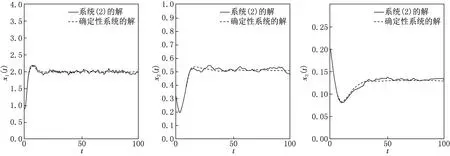
圖1 確定性系統和隨機系統(2)的持久性
(2) 3個物種將依概率滅絕.選取初始條件為(x1(0),x2(0),x3(0))=(0.9,0.3,0.2),t∈[-τ,0],a1=-0.7,a2=0.3,a3=0.1,b11=0.3,b12=0.2,b21=0.3,b22=0.5,b23=0.3,b32=0.4,b33=0.8,σ1=0.02,σ2=0.01,σ3=0.01.易驗證其滿足定理2.1結論(1),選取參數滿足r1<0.由Matlab軟件模擬系統解的圖像(圖2).由圖2可知,當白噪音很大時,捕食者和被捕食者均依概率死亡,這在確定性系統中是不會發生的.
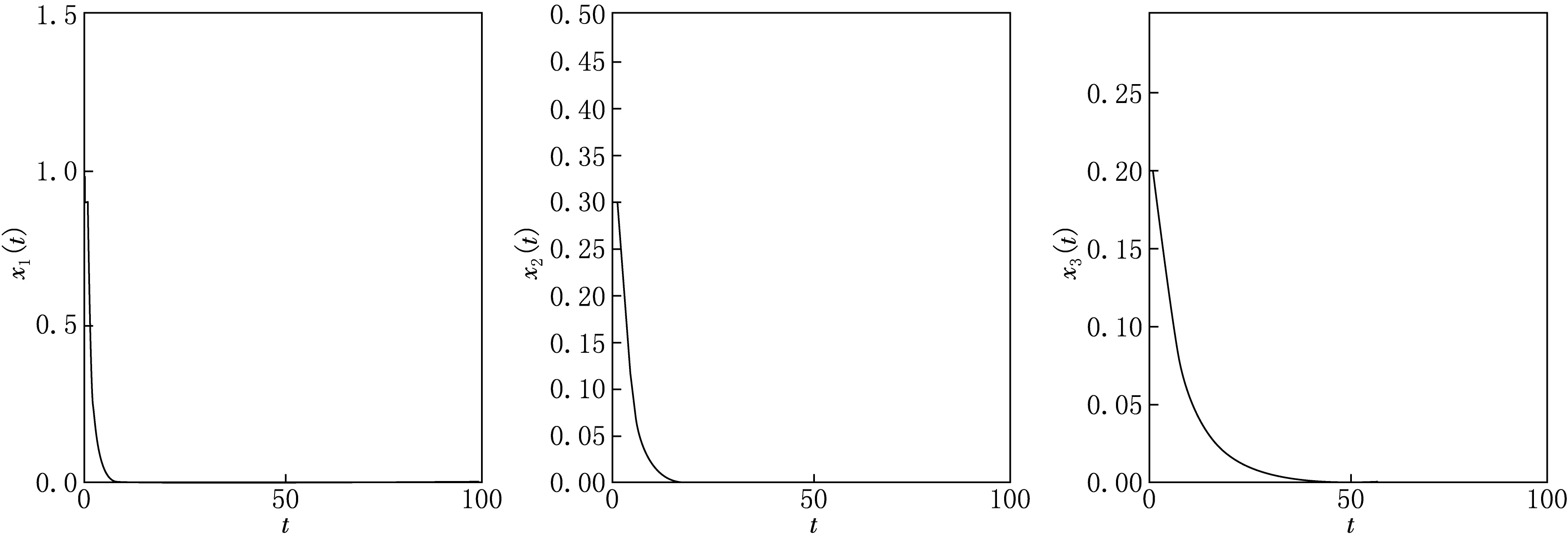
圖2 定理2.1當r1<0時,解的非持久性
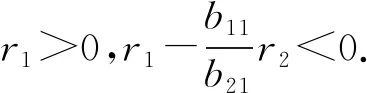
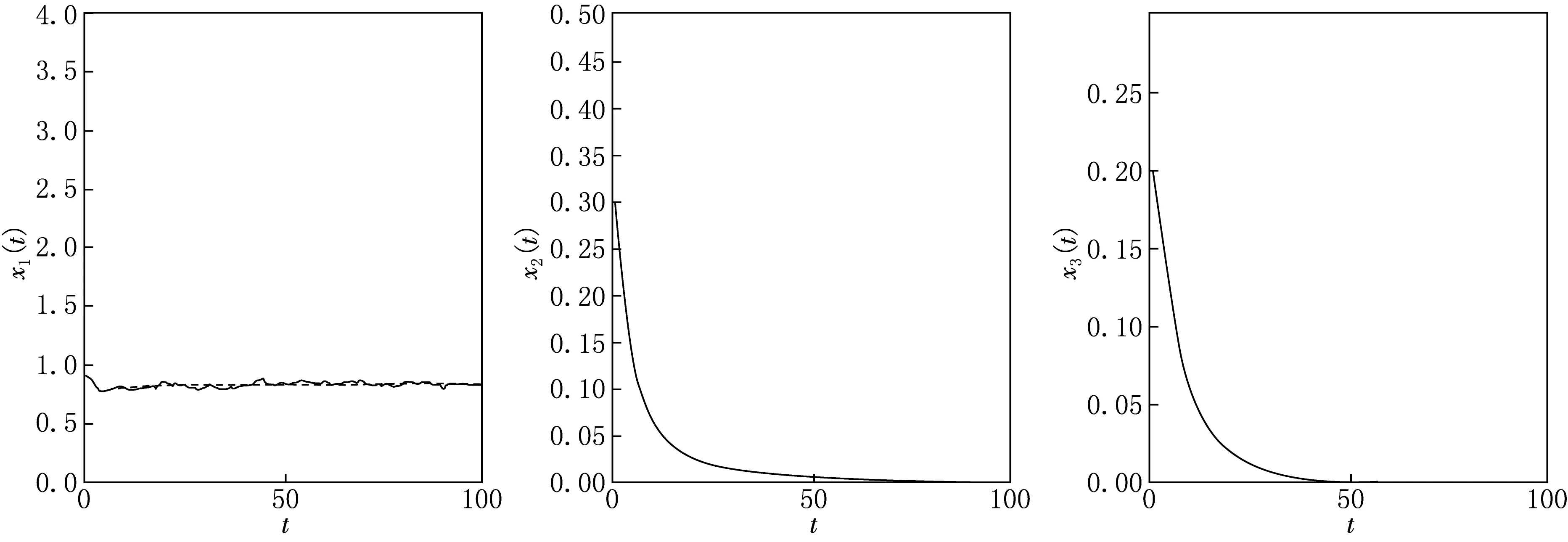
圖3 定理2.1當時,解的非持久性

