霍亂多斑塊傳播動力學建模及穩定性分析

李佳晶，周林華

(長春理工大學理學院，吉林 長春 130022)

0 引言

霍亂是一種急性腸道傳染病，盡管人們在努力限制其傳播，但它仍可引起暴發和大流行[1-5].其傳播方式在小范圍內主要是接觸傳播，而在大范圍內傳播時主要的傳播方式是水流傳播，特別是在衛生條件差的地方水流極易受到污染而增加霍亂的發生率.人們對霍亂普遍易感，病后可獲得一定免疫力.近年來，一些地方出現了霍亂暴發，包括海地(2010—2011年)、喀麥隆(2010—2011年)、肯尼亞(2010年)等[6].霍亂因其高致病性和快速傳播性，成為全球公共衛生和疾病防控體系最為關注的疾病之一.

鑒于流行病的特殊性，對流行病的研究不可能借助于實驗的手段，所以對其通過理論分析和模擬仿真來進行研究就顯得尤為重要.近年來傳染病微分方程模型被廣泛應用到控制傳染病流行的研究中，包括對霍亂的建模研究[7-21].Chao等[7]對海地霍亂暴發建立了隨機模型，分析了疫苗接種策略的影響.Eisenberg等[12]提出了一個多組模型來解釋海地霍亂的傳播，并確定最佳控制干預措施，但在證明地方病平衡點時模型只考慮了群體間的直接傳遞，忽略了群體間的間接傳遞.上述模型的分析在很大程度上依賴于數值模擬.Eisenberg等[13]建立了霍亂傳播的常微分方程模型，該模型包含直接和間接傳播、非線性發病率、病原體的多重感染狀態和感染個體的多重感染階段，其結果包含和擴展了許多先前的結果.

近年來關于霍亂模型的研究，就建模而言考慮的艙室對象均是在不可約網絡結構下的相關研究.然而，疾病的傳播往往是在各種復雜網絡系統之間進行，而對于可約網絡結構下的霍亂傳染病動力學建模與分析，至今沒有發現相應的結果.本文將在可約網絡結構下，考慮兩區域的SIR霍亂傳染病動力學模型及其穩定性分析.

1 海地霍亂傳播動力學建模

1.1 相關背景

2010年海地大面積暴發霍亂.疫情最初暴發于阿蒂博尼特地區并且迅速向海地西部等周邊地區蔓延.在阿蒂博尼特地區主要考慮3個受感染的城市，它們分別為Gona?ves、Saint-Marc和Dessalines；在海地西部同樣考慮3個受感染的城市，分別為Arcahaie、Léogne和Croix-des-Bouquets.其中Gona?ves市的霍亂細菌沿MEYE支流流入Léogne，Saint-Marc市的霍亂細菌沿MEYE支流分別流入Arcahaie市和Croix-des-Bouquets市.海地地圖和兩個地區中不同城市的代表點具體見圖1和表1.

圖1 海地地圖

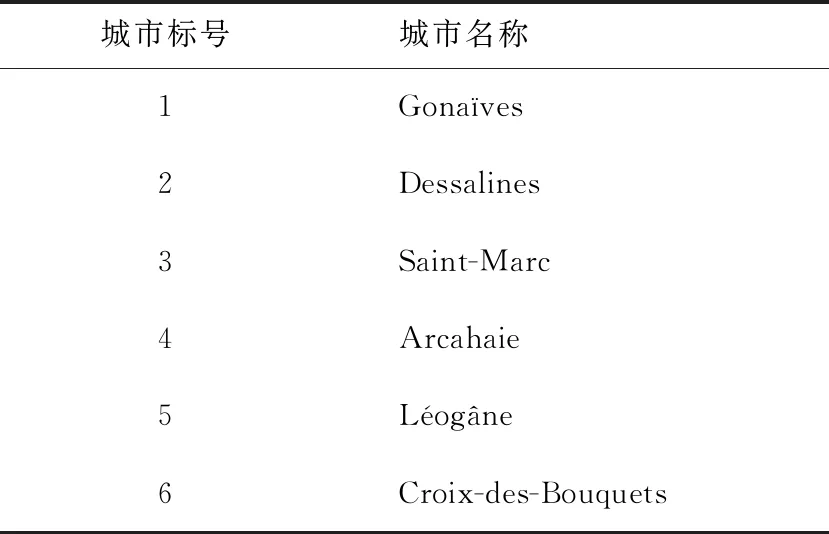
表1 城市對應點

1.2 模型的建立

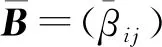
(1)

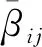
1.3 模型的約化

由可約矩陣定義，存在置換矩陣Q，使得

(2)

其中：Clk×lk是非負不可約矩陣；Al2×l1是非負矩陣.這里l1=l2=3，k=1，2.于是，模型(1)約化為

(3)

由文獻[26]的Next-Generation方法，令

則模型(3)的基本再生數為R0=ρ(M0)，其中ρ表示譜半徑.

由接觸矩陣B的形式，可將模型(3)分解為Cl1×l1和Cl2×l2兩個子系統，分別滿足：

(4)

(5)

當4≤i，j≤6時，Cl2×l2的子系統分下述兩種情形：

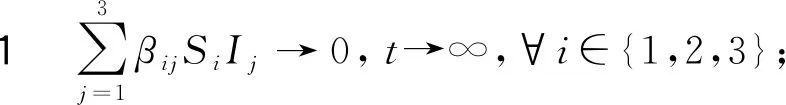
當滿足情形1時，Cl2×l2的子系統為

(6)

當滿足情形2時，Cl2×l2的子系統為

(7)

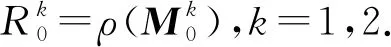
2 平衡點穩定性及證明

2.1 系統平衡點的穩定性

引理2.1設B=(βij)(1≤i，j≤3)是不可約矩陣.

引理2.2設B=(βij)(4≤i，j≤6)是不可約矩陣.

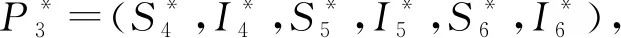
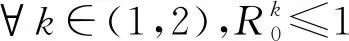
定理2.3設B=(βij)是可約矩陣，R0>1.

由文獻[22]的命題3.1和定理3.3知，本文上述引理2.1與引理2.2是成立的.同時，若定理2.1成立，則易得定理2.2與定理2.3.因此，下面重點構造Lyapunov函數以證明定理2.1.

2.2 定理2.1的證明

由于變量Ri沒有出現在模型(7)的前兩個方程中，所以考慮以下簡化系統：

(8)

易知模型(8)的可行域為

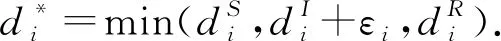
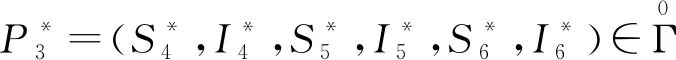
(9)

并且

(10)

構造模型(8)的李雅普諾夫函數

根據平衡點性質，以下等式成立：

(11)

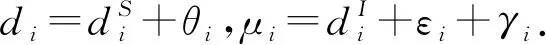
于是，沿系統(8)的解曲線對李雅普諾夫函數求導可得

(12)

(13)

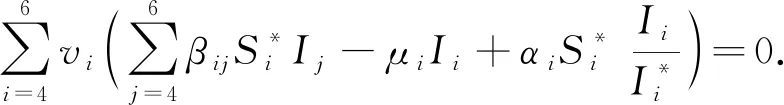
所以

(14)

其中：D(3；l)表示具有長度為l的定向循環的3個頂點的所有單圈圖的集合；CQ是在單圈圖Q屬于D(3；l)中具有長度為l的定向循環；E(CQ)和E(Q)分別代表CQ和Q中的弧.由文獻[22]有

(15)

進一步結合(14)和(15)式可得V′≤0.

3 數值模擬

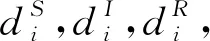
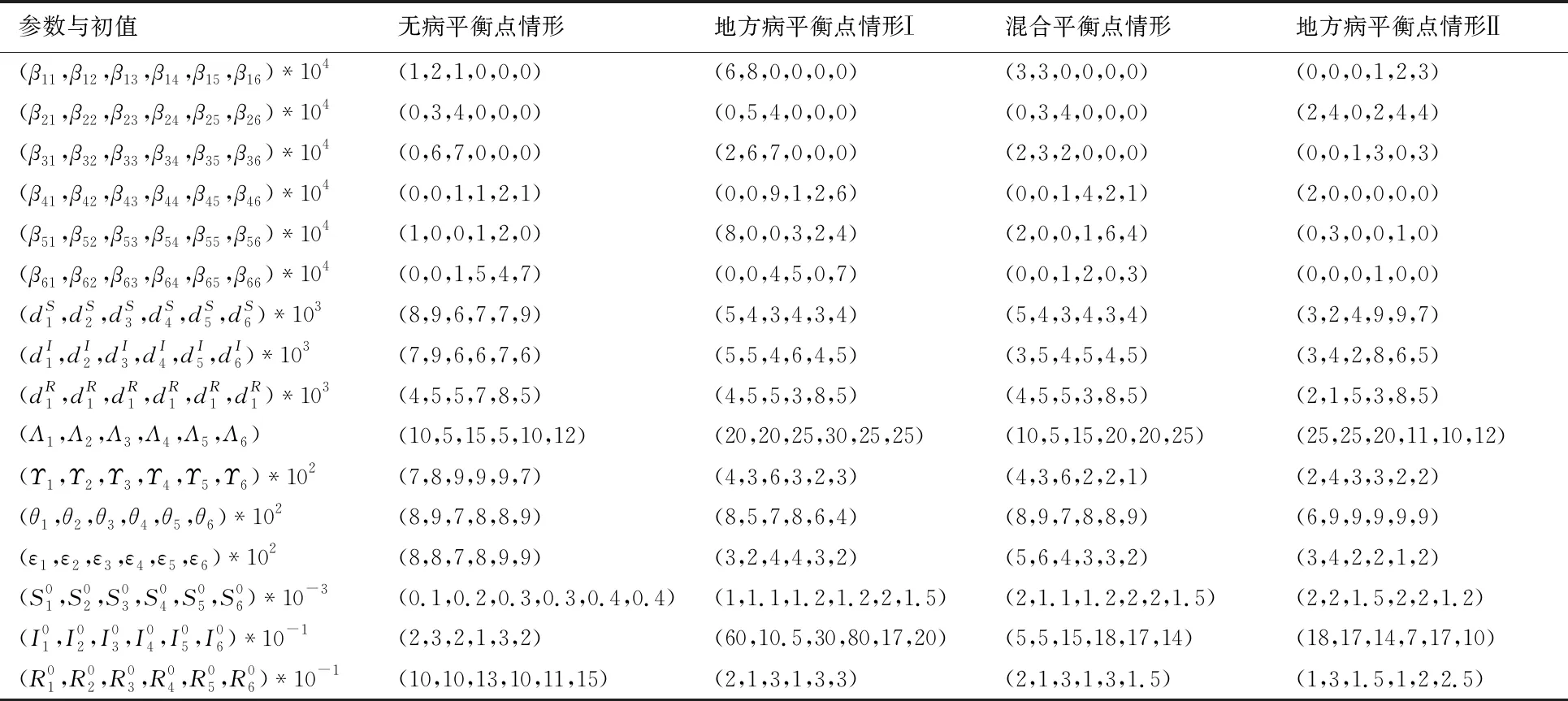
表2 參數取值及變量初值

(1) 無病平衡點情形

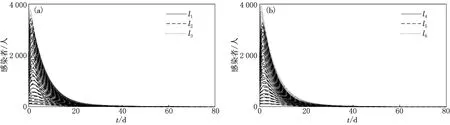
(a)第1組第2組

(2) 地方病平衡點情形Ⅰ

(a)第1組第2組

(3) 混合平衡點情形

(a)第1組第2組

(4) 地方病平衡點情形Ⅱ

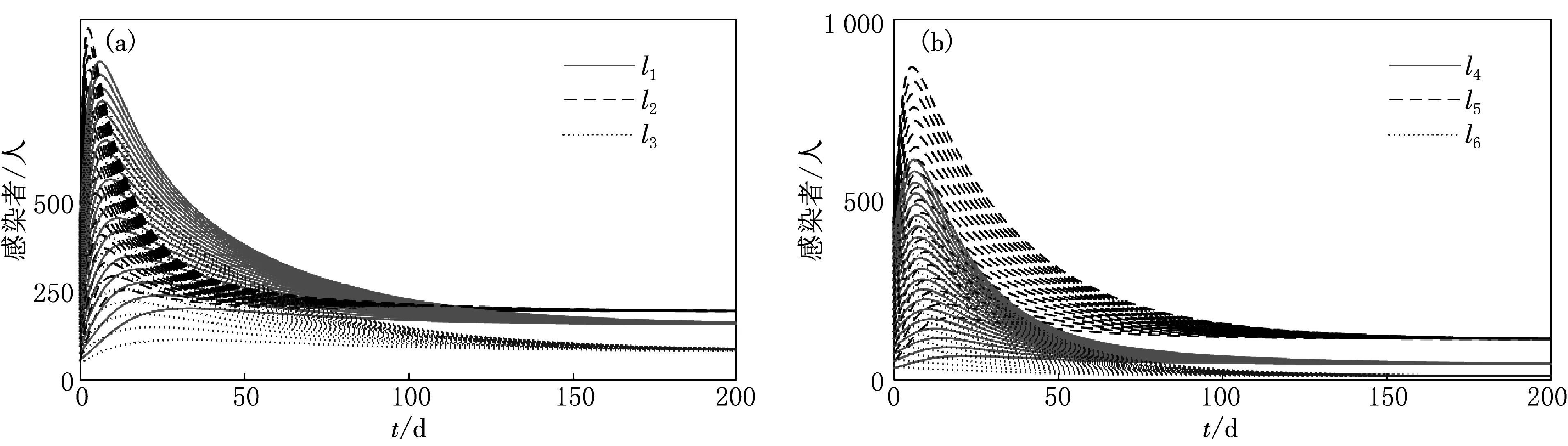
(a)第1組第2組

圖2—5中，I1，I2，I3代表3群體中第一組的染病者，I4，I5，I6代表3群體中第二組的染病者.

本文表明兩組SIR模型的全局漸近行為完全由基本再生數R0的大小確定.但和以往不同的是，在該結果中即使R0≤1也可能使霍亂疾病發生.因此對于霍亂疾病，除了要嚴格隔離治療病人和帶菌者外，還要杜絕人們喝生水、用生水浸泡蔬菜等習慣，防止外來霍亂細菌的入侵.