雙流制受電弓結構設計

馬 飛，陳 奎，周宇航，李明剛

（中車青島四方車輛研究所有限公司，山東 青島266031）

0 引言

受電弓是軌道車輛中重要的部件之一，用于將接觸網的電能傳導給車內高壓設備，為軌道車輛提供動力。雙流制受電弓需要滿足雙流制列車運營要求，適應交流和直流兩種供電制式接觸網。不同供電制式接觸網對弓網接觸的參數要求不同，但受電弓都應保持穩定的受流狀態，具備良好的受流質量。

雙流制受電弓的設計仍然遵循受電弓設計的基本規范，其結構設計內容一般包括運動學設計、機構動力學設計、結構設計和強度校核等，此外還需要進行電氣結構設計、弓網動力學分析等方面的工作。受電弓的結構設計是設計工作的基礎，由于雙流制受電弓實際工作范圍大，需要適應兩組不同工作參數，為設計工作增加了難度。本文在受電弓結構設計傳統方法的基礎上，結合動力學分析軟件，完成了雙流制受電弓結構參數設計，并對設計參數進行了復核和優化，提高了設計工作效率和結構的可靠性。

1 受電弓結構設計

雙流制受電弓主要是由底架、下臂桿、推桿、上臂桿、平衡桿、平衡臂以及弓頭等幾部分組成，形成空間連桿結構，如圖1所示。它以安裝在底架上的空氣彈簧為動力源，驅動下臂桿并帶動整個連桿機構實現升弓、降弓動作。同時，在升弓工作狀態時，空氣彈簧為其提供的恒定接觸力。

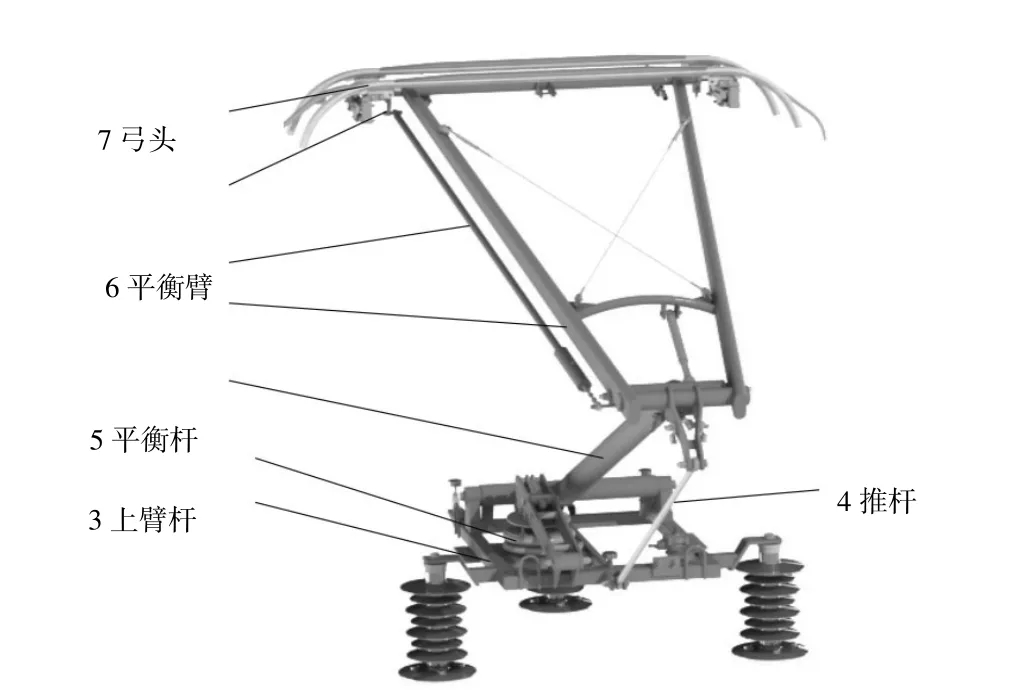
圖1 受電弓結構示意圖

受電弓的結構設計應盡可能保證在整個工作高度范圍內弓頭保持水平狀態，即弓頭平行度，以防止前后滑板接觸不均勻而造成弓頭偏磨和離線。另外要求工作高度范圍內，弓頭在車輛前進方向上的縱向偏移量應盡量小，以符合行業標準要求。在結構動力學方面，要求弓頭具有良好的接觸性能，即在整個工作高度范圍內具有相對恒定的靜態接觸力。由于不同制式接觸網的高度、網壓存在差異，雙流制受電弓的實際工作范圍更大，在不同制式接觸網的靜態接觸力也不相同，因此在設計過程中，需要先選擇一種工況進行參數計算，再進行另一種工況的參數校核。

1.1 計算模型

根據雙流制受電弓的結構組成和性能要求，按照傳統設計方法[1]，選定垂直于主軸和各鏈軸的對稱平面作為研究平面，將結構中各元件向該平面投影，并將各鉸鏈之間簡化成桿件，建立受電弓幾何關系計算模型，如圖2所示。圖中，P1-P2代表弓頭擺桿，下臂桿DBE為受電弓動作時的主動件。為了便于分析，建模時取推桿AC為主動運動件。

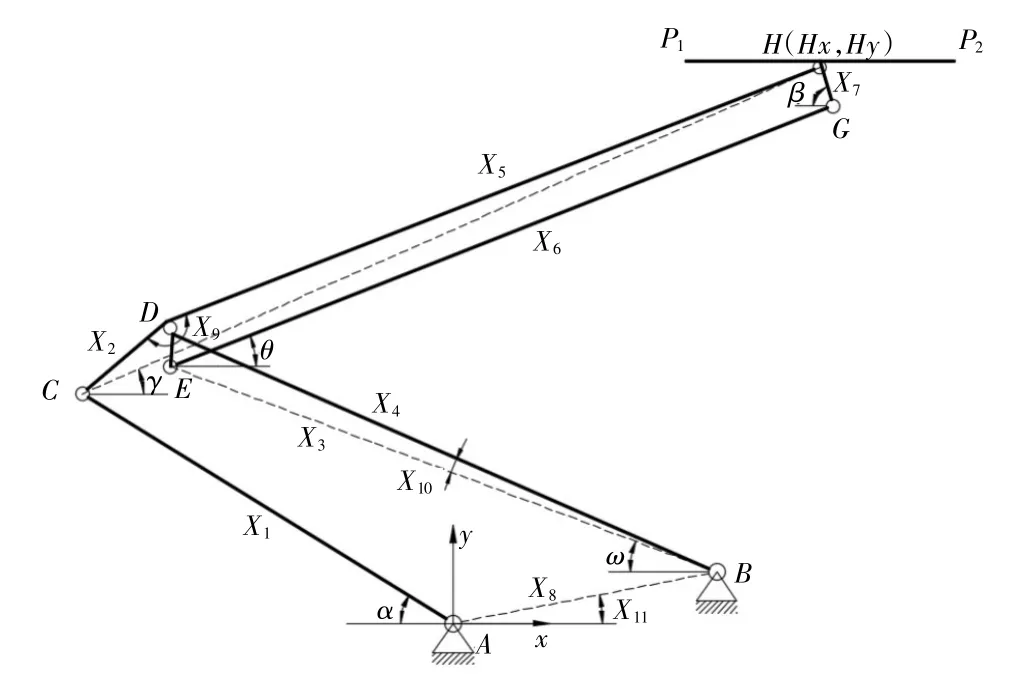
圖2 受電弓幾何關系計算模型

根據圖2，受電弓多連桿機構具有11個需要通過設計計算來確定的變量X1、X2……X11。根據受電弓結構設計要求，通過計算模型的幾何關系可以得到：

（1）H點的坐標

式中：lch是C點至H點的距離。

（2）弓頭平衡臂GH的偏轉角β

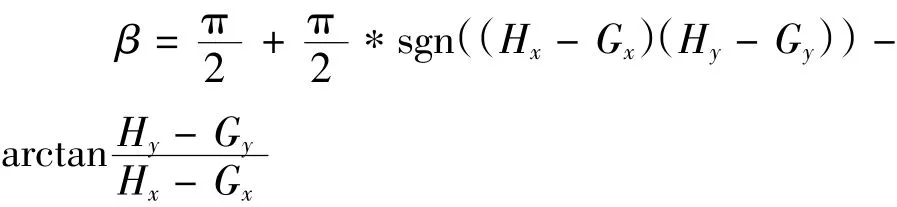
其中（Gx，Gy）為G點的位置坐標，其值為：

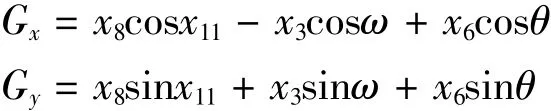
根據幾何關系分析可知，受電弓多連桿機構具有一個自由度，當推桿AC繞固定鉸支座A轉動時，弓頭H點的軌跡（Hx，Hy）及弓頭平衡桿GH與水平方向的夾角β就可以唯一確定，即：

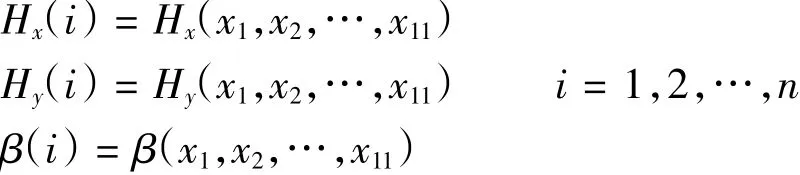
式中：Hx（i）為弓頭H點軌跡曲線離散點的x坐標分量；Hy（i）為弓頭H點軌跡曲線離散點y坐標分量；β（i）為弓頭平衡臂在第i個位置與水平方向的夾角；n為離散點數量。

1.2 結構幾何參數設計

受電弓結構幾何參數設計屬約束非線性連續變量最優化設計問題。求解約束非線性問題的方法有多種[2]，此處不再贅述。根據受電弓結構設計要求，應保證在工作高度范圍內平衡桿GH應盡量平動，且弓頭H點縱向位移盡可能小。根據對多目標問題的求解方法，將多目標問題轉化成一個或一系列的單目標問題，即根據設計目標重要程度，選擇平衡桿GH平動作為主要設計目標，而將H點的縱向位移轉化為約束條件。即機構優化的目標函數為：

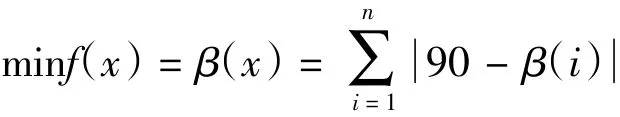
各個設計變量應滿足：

（1）受電弓正常工作高度范圍內，弓頭H點軌跡曲線縱向偏移盡量小，即：

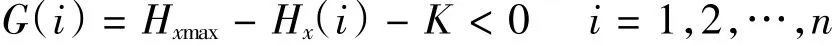
其中：Hxmax為離散點x坐標分量的最大值；K為H點允許縱向位移最大值。

（2）為保證正常收弓，受電弓初始位置應能滿足：

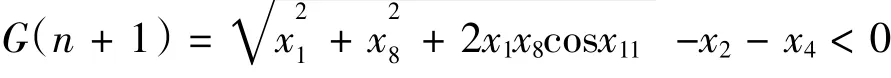
（3）受電弓的升弓高度應滿足要求，即弓頭H點的y方向坐標滿足：

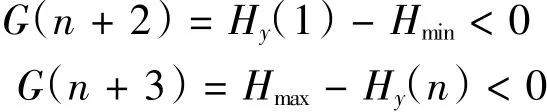
其中，Hmin和Hmax分別為受電弓最小工作高度和最大工作高度。

上面（1）～（3）中G（i）＜ 0，（i=1，2，…，n+1，n+2，n+3）為n+3個不等式約束條件。

對數學模型進行尺度變換，保證數學模型有更好的收斂性和穩定性。確定各個設計變量的數值范圍，并利用建立的受電弓數學模型和優化目標函數及約束條件進行編程計算[3]，就可獲得受電弓幾何參數設計結果。

2 結構設計校核與分析

以上設計方法解決了受電弓結構設計中的幾何參數問題，可以通過動力學分析軟件進行受電弓結構動力學建模，對設計參數進行校核和進一步優化。

2.1 結構動力學建模

在初步確定幾何參數后，可借助動力學分析軟件ADAMS進行受電弓結構動力學建模。按照雙流制受電弓的結構和幾何關系計算模型，在模型中保留主要部件，整個模型的基準點選取在受電弓前部絕緣子底面中心處，如圖3所示。

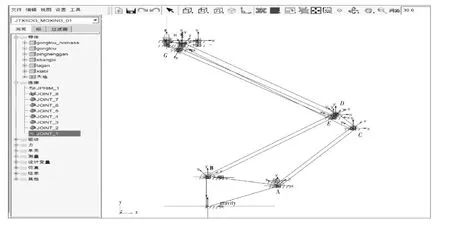
圖3 受電弓結構動力學分析模型

2.2 結構參數的分析和優化

2.2.1 相關性分析

對設計參數進行優化，首先應對優化目標進行參數相關性分析，尋求與之密切相關的變量。將模型設置為參數化模型，利用ADAMS軟件相關性分析功能[4]，對弓頭平行度、弓頭縱向偏移量和接觸力變化率等進行參數相關性分析，得到：

（1）弓頭平行度與受電弓平衡桿長度X6（E點、G點坐標值）參數密切相關；

（2）弓頭縱向偏移量與受電弓上臂桿和推桿的連接位置C點坐標值相關性較高；

2.2.2 弓頭平行度

受電弓弓頭平行度分析即是對幾何關系模型中GH桿的平動驗證和優化，利用ADAMS參數化模型和參數優化功能，尋求弓頭角度變化率最小時各主要變量參數值。從圖4優化后受電弓工作高度與弓頭傾角的關系曲線圖中可以看出，在工作高度范圍740 mm～2 920 mm內，受電弓弓頭傾斜角度范圍為-1.0°～ 0.4°內。

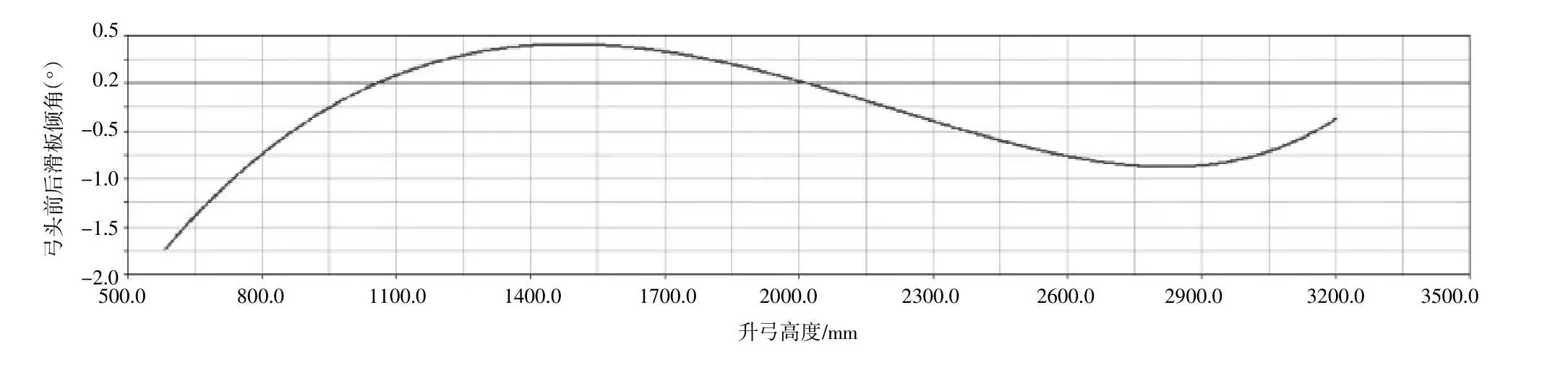
圖4 受電弓弓頭傾角變化曲線

2.2.3 弓頭縱向偏移量

弓頭縱向偏移量分析即是對受電弓幾何關系模型中H點工作高度范圍內的縱向位移量驗證和優化。對相關性較高的參數進行優化分析后，得到受電弓弓頭H點縱向運動軌跡曲線，如圖5所示。在此雙流制受電弓工作高度范圍740 mm～2 920 mm內，弓頭H點的縱向位移約47.5 mm，符合行業標準要求[5]。

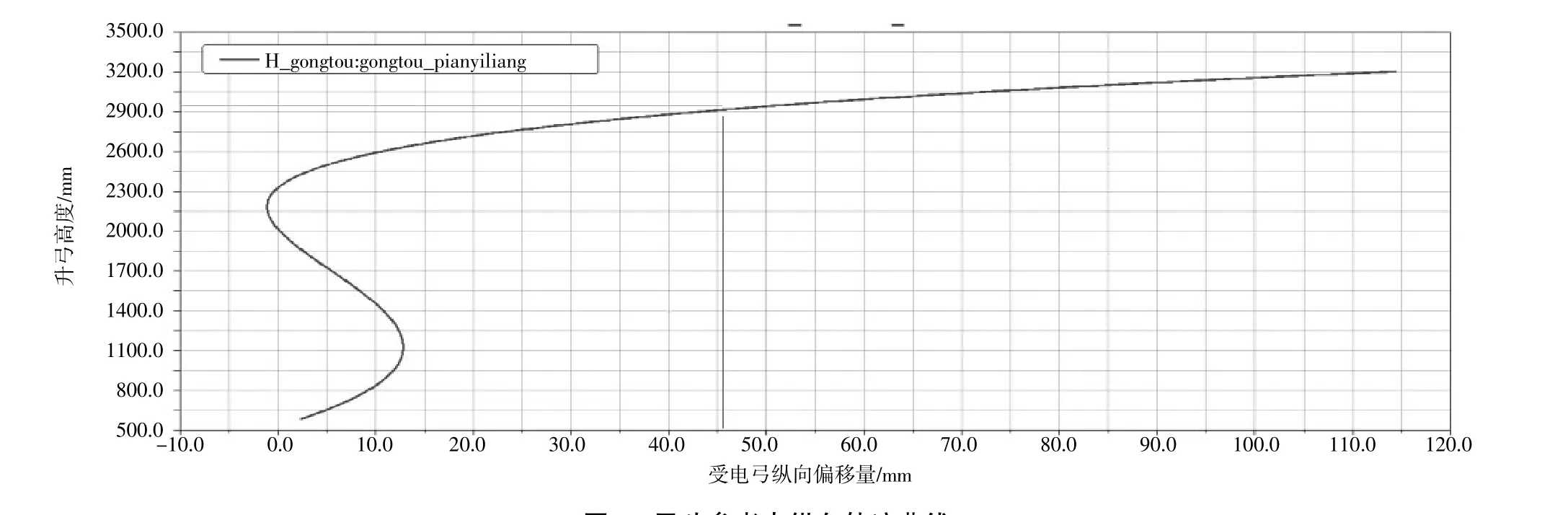
圖5 弓頭參考點縱向軌跡曲線

3 結構動力學分析

通過上述方法，解決了受電弓結構設計中的幾何參數優化問題，還需要解決在受電弓兩種工況下工作高度范圍內靜態接觸力保持恒定的技術要求，并求解驅動力參數。

恒定靜態接觸力是受電弓重要的性能指標之一，通過對動力學分析模型的修改，增加驅動元件，可實現對受電弓接觸力的仿真分析。根據仿真分析結果，雙流制受電弓對不同制式接觸網具備不同靜態接觸力，其接觸力的值是由空氣彈簧內充入壓縮空氣壓力決定的，而工作高度范圍內靜態接觸力變化率則是與下臂桿驅動弧形板的外廓曲線密切相關，弧形板的外廓曲線是通過樣條曲線擬合而成。

仿真分析得到在不同制式接觸網工作時，受電弓靜態接觸力與工作高度關系曲線如圖6所示，圖中曲線不平順是因模型中弧形板與鋼絲繩接觸設置導致的。根據空氣彈簧參數，可以進一步得到空氣彈簧工作氣源壓力。在受電弓工作高度范圍內，直流接觸網下，靜態接觸力最小及最大值分別為117 N和122 N，空氣彈簧輸入壓力0.435 MPa；交流接觸網下，靜態接觸力最小及最大值分別為68.5 N和73 N，空氣彈簧輸入壓力0.390 MPa，均符合行業標準要求。

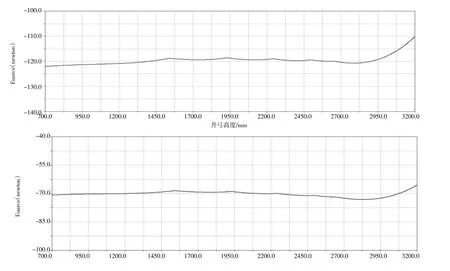
圖6 直流接觸網和交流接觸網受電弓靜態接觸力仿真曲線

4 試驗驗證

通過雙流制受電弓結構參數優化設計方法，得到受電弓結構幾何參數和驅動力參數，根據參數進行結構設計和強度校核等工作，完成了產品設計。利用受電弓性能試驗臺，按照行業標準進行性能試驗測試，并將測試結果與仿真分析結果進行對比。通過數據對比分析可知，雙流制受電弓的試驗接觸力曲線與仿真數據基本一直，數據在行業標準要求范圍之內，升弓和降弓過程中的誤差是由空氣彈簧特性和結構中鉸接位置的摩擦力引起的。

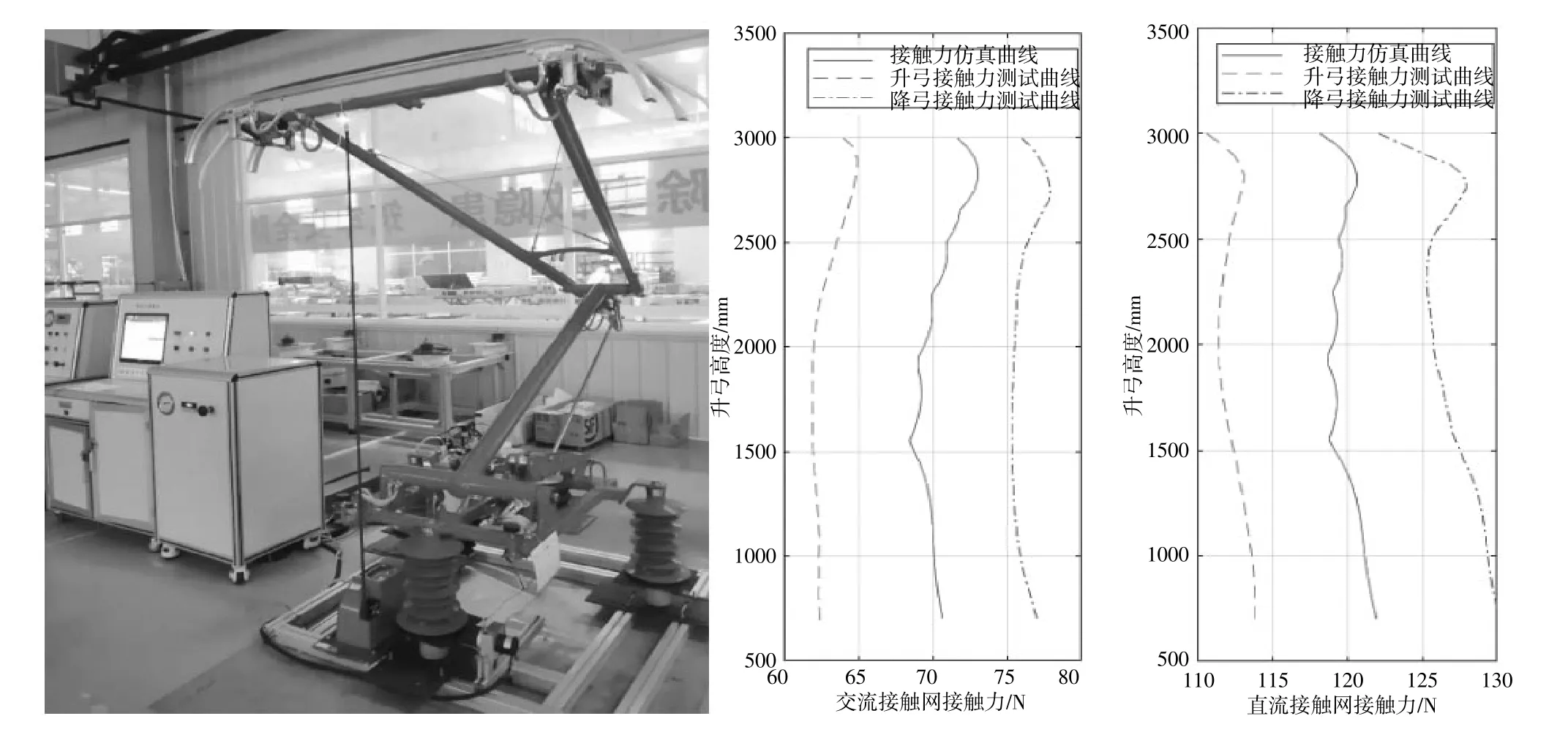
圖7 受電弓性能試驗與測試數據對比

5 結論

利用傳統方法進行雙流制受電弓結構初步設計，初步確定受電弓結構的幾何參數。在此基礎上，利用動力學分析軟件建立結構動力學參數化建模，對受電弓弓頭平行度、弓頭縱向偏移量、靜態接觸力等重要指標進行參數相關性分析，尋求各個指標的強相關參數。對弓頭平行度、弓頭縱向偏移量等指標進行校核并進一步完成參數優化，對弓頭靜態接觸力進行仿真分析，完成對驅動力參數的計算。通過傳統設計方法和動力學模型分析相結合，簡化了設計方法，提高了設計效率和設計參數可靠性。產品的性能試驗結果表明，受電弓靜態接觸力符合相關標準要求并與理論分析基本一致，證實了設計方法的有效性。