活性破片侵徹不同厚度鋁靶的數值模擬
劉 露,唐恩凌,陳 闖
(沈陽理工大學裝備工程學院,沈陽110159)
活性破片依靠動能侵徹和內爆相結合的毀傷機理聯合作用提高戰斗部的毀傷能力,Al/PTFE是典型的活性破片。M.N.Raftenberg[1]等針對質量比為74∶26的PTFE/Al配方活性材料,通過Hopkinson桿動態壓縮實驗和準靜態壓縮實驗,獲得了活性材料的動態和靜態力學參數,利用所獲實驗參數分別對Johnson-Cook強度模型和PSD強度模型進行了標定,并且分別基于PSD模型和Johnson-Cook模型采用數值模擬方法對活性破片沖擊金屬靶作用行為進行了研究,結果表明標定后的數值模擬材料模型能較好反映活性材料相關力學行為。R.G.Ames等[2]通過泰勒桿實驗對含能破片臨界起爆壓力閾值進行了測試,分析了活性材料點火起爆機理,還利用密閉容器實驗測試了活性材料撞擊起爆壓力時程曲線。本文研究了不同算法對活性破片侵徹不同厚度鋁靶仿真結果的影響,選擇SPH算法對活性破片侵徹不同厚度鋁靶進行數值模擬,得到不同撞擊速度下靶板碎片速度的變化。
1 數值模擬
采用Autodyn有限元軟件對Al/PTFE活性破片侵徹鋁靶的過程進行二維數值模擬,彈靶均采用Johnson-Cook強度模型,均選擇Shock狀態方程,采用軸對稱模型。仿真模型如圖1所示。

圖1 仿真模型
選取Lagrange、Euler和SPH三種算法進行仿真。Lagrange算法劃分的每個單元網格的頂點隨材料一起變形,算速度比其他算法要快,但材料的大變形也會使網格發生變形,從而導致計算精度嚴重下降甚至難以計算下去。Euler算法劃分的網格不發生扭曲,物質通過單元格邊界流入流出,材料的大變形或流動不會導致網格的畸變,缺點主要是必須追蹤物質的運動,計算時間相對較長。SPH算法將材料分解為一系列具有質量、速度和能量的粒子,不需要劃分網格,廣泛用于模擬連續體結構的解體等大變形問題,能保證計算精度。
截取了在使用三種算法時的幾張過程圖進行對比分析,三種算法下的活性破片侵徹靶板的過程分別如圖2~圖4所示。

圖2 Lagrange算法下的活性破片侵徹靶板過程
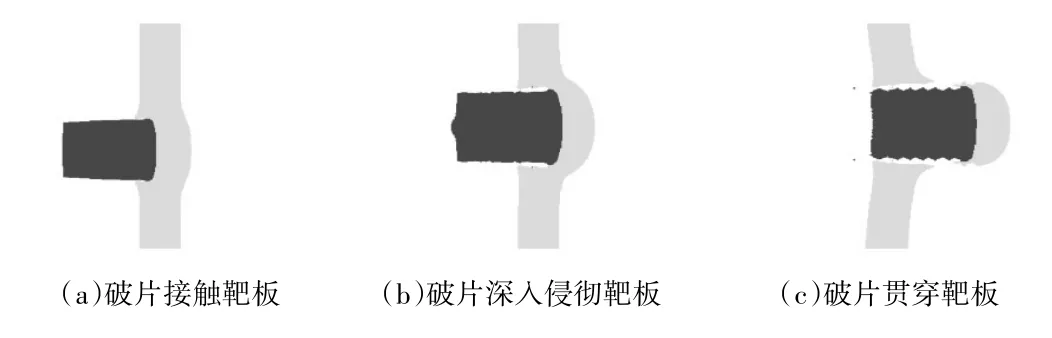
圖3 Euler算法下的活性破片侵徹靶板過程

圖4 SPH算法下的活性破片侵徹靶板過程
比較圖2~圖4可知,Lagrange和Euler算法下的侵徹過程只顯示了破片貫穿靶板的常規過程,而未表現出活性破片碎裂的過程,無法實現活性破片撞擊靶板之后碎裂形成碎片云,因此,不能完成爆炸毀傷和動能穿透的聯合毀傷效果。由活性破片破碎原理可知,破片的破碎是由于拉伸應力波的作用所致。SPH算法較好地反映了侵徹過程中破片的破碎,
由上述比較可以看出,SPH算法在諸多方面都優于Lagrange算法和Euler算法,SPH算法能夠較真實的反映活性破片碎裂的過程,因此采用SPH算法對活性破片侵徹不同厚度鋁靶進行數值模擬。
2 仿真結果
通過對Al/PTFE藥柱以不同速度垂直侵徹鋁靶板進行數值模擬,分析碰撞速度對其毀傷效應的影響。活性材料的參數為φ10 mm×10 mm。靶板厚度分別取3 mm、4 mm和5 mm。撞擊速度取400 m/s-1~ 1 200 m/s-1,速度梯度取 400 m/s-1。
厚度的不同會導致靶板碎片的速度有很大差異,導致的二次毀傷效果差異明顯。將靶板碎片速度的變化提取出來,比較靶板碎片速度的變化,變化曲線如圖5所示。
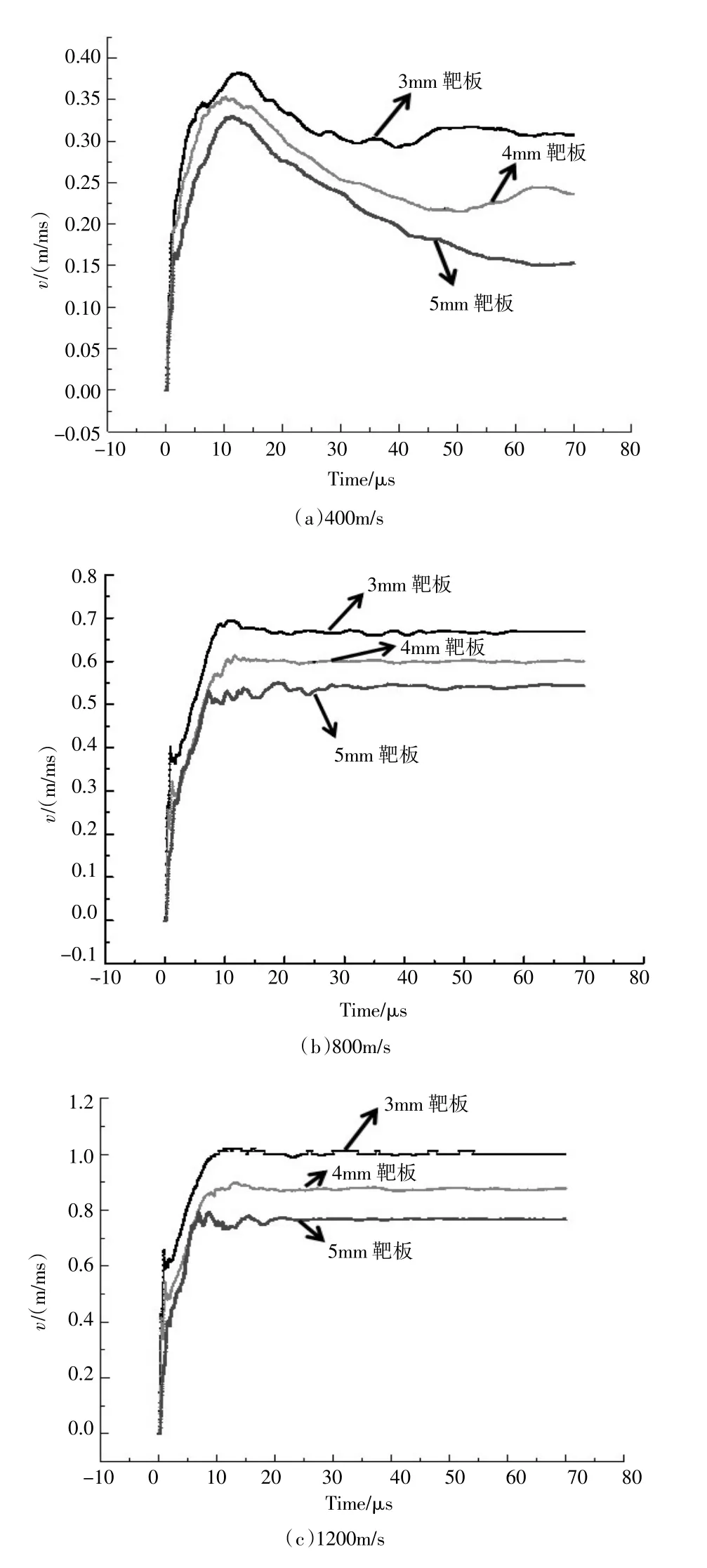
圖5 靶板碎片速度變化曲線
由圖5可以看出,當撞擊速度為400 m·s-1(圖5a),靶板碎片速度先迅速升高,隨后呈下降趨勢,當靶板厚度為5 mm時下降最明顯,當撞擊速度為800 m/s-1,靶板碎片速度升高至最高點后逐漸趨于穩定,隨著撞擊速度的增大,穩定趨勢更加明顯。
隨著靶板厚度的增加,靶板碎片的速度峰值遞減,400 m/s-1侵徹靶板時,侵徹時間較長,破片速度穩定的時間較長。由比較可知,破片的撞擊速度越高,靶板碎片速度達到穩定的時間越短,且靶板碎片速度峰值越大。在相同的撞擊速度下,靶板厚度越厚,靶板碎片峰值速度相對撞擊速度的衰減值越大。
不同靶板厚度的靶板碎片峰值速度相對撞擊速度衰減的百分比在5%~35%的范圍,隨著活性破片初始速度的提高,速度衰減百分比基本呈上升趨勢,尤其5 mm的靶板趨勢更為明顯;同樣的撞擊速度下,靶板越厚,靶板碎片峰值速度相對撞擊速度衰減的百分比越大。
3 結束語
本文采用Autodyn-2D非線性動力學軟件對活性破片侵徹鋁靶進行了數值模擬,得到不同算法對仿真結果的影響,運用SPH算法仿真研究了靶板厚度對毀傷效果的影響。在相同靶板厚度下,隨著活性破片撞擊速度的提高,靶板碎片速度達到穩定的時間越短,靶板碎片峰值速度相對撞擊速度的衰減值越大。在相同的撞擊速度下,靶板越厚,靶板碎片峰值速度相對撞擊速度衰減的百分比越大。

