基于改進TOPSIS 法的艦船裝備技術狀態評估方法

曹 蒙，陳 博

(1.中國人民解放軍91404 部隊91 分隊，河北 秦皇島 066001；2.海軍駐上海地區第一軍事代表室，上海201913)

0 引言

隨著艦船裝備制造工藝、傳感器技術、多源信息處理能力的發展，操管人員對裝備監控的維度逐漸增多，對裝備技術狀態的評判也由原來的“聽、摸、聞”等定性分析，變為監測數值的定量診斷［1］。但升級換代的同時，也帶來了兩個問題，一是裝備的監控系統僅是對各個獨立參數的監控，少數幾個指標的超標告警，無法說明裝備整體的技術狀態；二是監測維度眾多，沒有整體性指標的描述，給綜合判斷增加了難度。

目前，對這類問題，部分學者做了一些研究，采用的方法主要有神經網絡、 主成分分析、 支持向量機、馬爾科夫理論以及這些方法的組合［2-4］。上述方法都是將多個指標融合成一個虛擬指標，再通過待測狀態與“良好、合格、不合格”等分級狀態指標的比較，實現綜合判斷。但在實際運用中，等級之間的狀態很難界定。同時，處于故障狀態下的設備，監測數據變化劇烈，且是一個逐漸惡化的過程，無法準確通過監測數據描述當前狀態。為此，本文改進了TOPSIS法，并結合模糊理論，考慮指標權重信息，建立了綜合評估模型，很好地解決了上述問題。

1 改進的 TOPSIS 法

TOPSIS 法是 1981 年由 C.L.Hwang 和 K.Yoon 提出的，核心思想是依據樣本點與“最優解”、“最劣解”的相對接近度，實現對分析目標的優劣評判。在實際應用中，“最優解”容易獲得，一般可將穩定狀態下設備參數的運行值作為最優解集。但“最劣解”卻無法準確度量，主要是難以確定“最劣解”的評判基準。另一方面，傳統TOPSIS 法未考慮評估參數的權重，造成了數據信息的丟失。對此，本文引入參數權重，以樣本點到最優解的加權距離作為評估依據，實現裝備的技術狀態評估。

1.1 評估流程

裝設備的技術狀態評估是一個復雜的過程，主要包括評估參數的數據采集、預處理、權重計算、狀態評估、結果解釋等步驟，如圖1 所示。

圖1 評估流程

1.2 數據預處理

本文采用模糊理論對數據預處理，該理論是1965 年L.A.Zadeh 提出的，主要是通過隸屬函數將難以界定、模糊不清的狀態數值化，為后續量化分析作準備。主要步驟：

(a)構建隸屬函數

對于處于穩定工況下的裝備，其監測參數會在某一數值附近波動，且呈現正態分布規律。由此，以一段穩定工作時間內，各監測參數的平均值、方差建立正態分布形式的隸屬函數。

式中，u(j)、σ2(j)分別表示第j 個參數的平均值、方差，x 為評估參數的實時監測值。

(b)計算隸屬度

將樣本點數據帶入公式(1)，計算隸屬度，形成隸屬度矩陣。

上述過程，通過隸屬函數的引入，將監測數據映射到［0，1］區間，實現了數據信息的進一步提取。其中，隸屬度越接近1，表明狀態越好；反之，則差。

1.3 權重計算

本文采用熵權法確定參數的權重，以m 個樣本，n 個參數的研究對象為例，具體步驟為：

(a)數據標準化

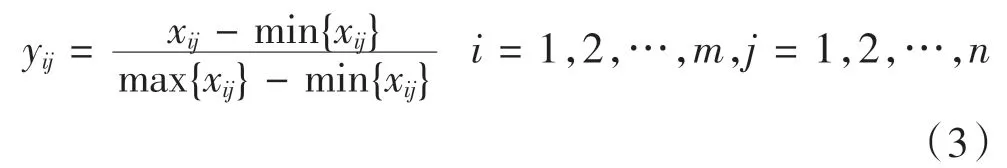
式中，xij為評估參數值，yij為標準化結果。

(b)計算信息熵和效用值

第j 項參數的信息熵為：

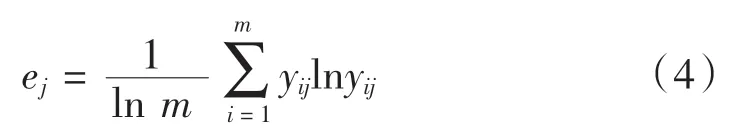
信息效用值為：

(c)確定權重

第j 項參數的權重為：

1.4 狀態評估

在完成數據預處理、獲得參數權重后，以樣本點到“最優解”的加權距離作為評估依據，實現狀態評估。

(a)確定最優解

(b)計算樣本點到基準點的加權距離

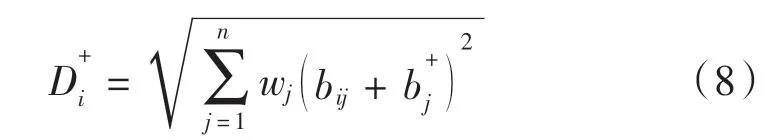
(c)基于最優解的接近度計算

由此，得到改進TOPSIS 法的接近度評估參數，數值越大表示該樣本與最優狀態接近度越高，技術狀態就越好。

2 計算驗證

以文獻［5］中6-135 型廢氣渦輪增壓柴油機為例，選取最大燃燒壓力、油耗率、排溫、增壓器轉速4個指標進行分析。柴油機正常狀態及待評估狀態如表1 所示。

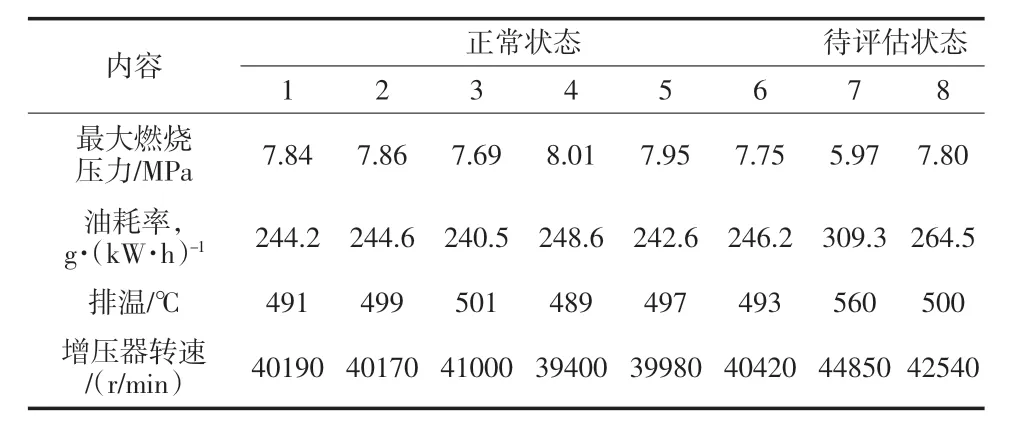
表1 工況參數值

2.1 確定隸屬函數

根據正常狀態1～6 的記錄值，計算各指標的均值與方差，結果如表2 所示。

表2 均值與方差

則各參數隸屬函數如下：

2.2 計算隸屬度

將待評估狀態7、8 的記錄值帶入隸屬函數，得到隸屬度矩陣：

2.3 綜合評估

以表16 個正常狀態的數據為基礎，按公式(3-6)計算指標參數權重：

以各指標均值作為最優解集，按公式(8-9)可計算的待評估狀態與最優解的加權距離和接近度分別為：

通過數據分析，可以看出，狀態8 好于狀態7，此評估結果與“7 為故障狀態，8 為基本正常狀態”的實驗設計一致。由此，驗證了本方法的正確性。另外，進一步分析，對于個指標的評估對象，若處于良好狀態，則各指標隸屬度接近于1，可計算得綜合評估的加權距離接近0；同理，若處于故障狀態，則各指標隸屬度接近于0，可計算得綜合評估的加權距離接近1。綜合分析可知，對于個指標的評估對象，其加權距離在區間內。

3 結束語

本文對于難以區分等級狀態的裝備監測值，采用模糊理論，進一步量化。同時，針對故障狀態下，裝備監測數據失真，評估基準無法確定的問題，提出了基于“最優解”距離的評估原則。另外，引入指標權重因素，使得評估模型包含了更多的數據信息，增強了模型的說服力。最后，通過實例分析，驗證了方法的正確性、適用性，并對多指標對象的評估結果做了進一步分析。