風(fēng)力發(fā)電機(jī)組鑄造主軸脹套聯(lián)接應(yīng)力測(cè)量與分析
裘 園,何先照,應(yīng)華冬
(1. 浙江運(yùn)達(dá)風(fēng)電股份有限公司,杭州310012;2. 浙江省風(fēng)力發(fā)電技術(shù)重點(diǎn)實(shí)驗(yàn)室,杭州310012)
鑄造工藝具備成品率高,質(zhì)量穩(wěn)定,便于批量生產(chǎn)的特點(diǎn),因此風(fēng)力發(fā)電機(jī)組主軸廣泛開(kāi)始采用鑄造工藝進(jìn)行生產(chǎn)。而風(fēng)力發(fā)電機(jī)組主軸與齒輪箱的聯(lián)接,主要采用脹緊套聯(lián)接的形式,該聯(lián)接方式具備構(gòu)造簡(jiǎn)單,傳扭能力高,抗沖擊載荷等的優(yōu)點(diǎn)[1]。為了能夠?qū)⒅鬏S的扭矩傳遞給齒輪箱,脹緊套對(duì)主軸必須要有足夠的抱緊力。陜西科技大學(xué)的張鋒等介紹了運(yùn)用拉梅方程來(lái)設(shè)計(jì)脹緊套的理論算法[2],重慶大學(xué)的杜靜等使用有限元軟件分析了不同的間隙和摩擦系數(shù)對(duì)脹緊套接觸應(yīng)力的影響[3],何章濤等對(duì)拉梅方程理論計(jì)算和有限元分析結(jié)果做了對(duì)比[4]。為了將理論計(jì)算和有限元分析結(jié)果與實(shí)際應(yīng)力進(jìn)行比較,對(duì)某大MW 風(fēng)電機(jī)組的脹緊套進(jìn)行應(yīng)力測(cè)量試驗(yàn),在主軸鋼套內(nèi)側(cè)貼應(yīng)變片,通過(guò)測(cè)量脹緊套安裝前后剛套內(nèi)表面的應(yīng)變值,從而獲得剛套內(nèi)表面的應(yīng)力變化,將拉梅方程的理論計(jì)算結(jié)果和有限元仿真結(jié)果進(jìn)行對(duì)比,從而為主軸和脹緊套的設(shè)計(jì)優(yōu)化提供參考。
1 脹緊套工作原理
風(fēng)力發(fā)電機(jī)組主軸、 脹緊套與齒輪箱的裝配關(guān)系如圖1 所示,主軸將風(fēng)輪葉片產(chǎn)生的扭矩通過(guò)脹緊套傳遞到齒輪箱,經(jīng)過(guò)齒輪箱增速后傳遞給發(fā)電機(jī)。脹緊套參照標(biāo)準(zhǔn)《JB/T 7934-1999 脹緊聯(lián)結(jié)套型式與基本尺寸》設(shè)計(jì),其結(jié)構(gòu)詳見(jiàn)圖1,通過(guò)擰緊收縮盤內(nèi)外環(huán)之間的螺栓,產(chǎn)生軸向拉伸力,經(jīng)過(guò)內(nèi)外環(huán)錐面轉(zhuǎn)變?yōu)閺较虻谋Ьo力,使行星架抱緊主軸,從而產(chǎn)生足夠的靜摩擦力,將主軸的扭矩傳遞到齒輪箱。同時(shí)在收縮盤內(nèi)外環(huán)設(shè)計(jì)了一個(gè)止口,通過(guò)止口來(lái)限制收縮盤內(nèi)外環(huán)的相對(duì)位移,從而既保證脹緊套有足夠的扭矩傳遞能力,又不至于使各部件的應(yīng)力超過(guò)許用應(yīng)力。
2 理論計(jì)算
如圖1 所示,擰緊收縮盤內(nèi)外環(huán)之間的螺栓后,收縮盤外環(huán)沿斜面滑移后,脹緊套各個(gè)接觸面之間將產(chǎn)生變形和接觸壓力。根據(jù)變形協(xié)調(diào)條件計(jì)算出各個(gè)接觸面之間的接觸壓強(qiáng)后,將各部件等效為厚壁圓筒模型,運(yùn)用拉梅方程算出各個(gè)部件內(nèi)外表面的應(yīng)力。
假設(shè)鋼套外徑位移為δ,主軸外徑位移量為△1,主軸內(nèi)徑位移量為△2,行星架外徑位移量為△3,行星架內(nèi)徑位移量為△4,收縮盤內(nèi)環(huán)內(nèi)徑位移量為△5。經(jīng)過(guò)測(cè)量,主軸內(nèi)徑與鋼套外徑之間的間隙△d2=-0.04 mm,主軸外徑與行星架內(nèi)徑之間的間隙△d1=0.052 mm,行星架外徑與收縮盤內(nèi)徑之間的間隙△d0= 0.0885 mm。脹緊套各部件的材料性能如表1所示。
根據(jù)變形協(xié)調(diào)條件,接觸面位移差等于各接觸面之間的間隙,可得:
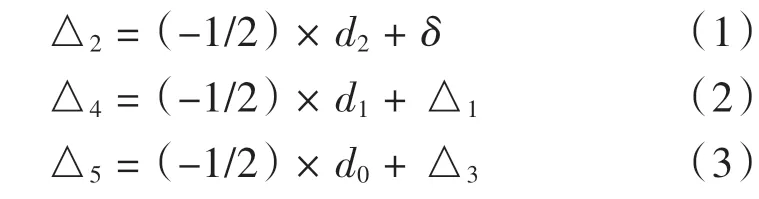
收縮盤內(nèi)環(huán)內(nèi)徑位移量:
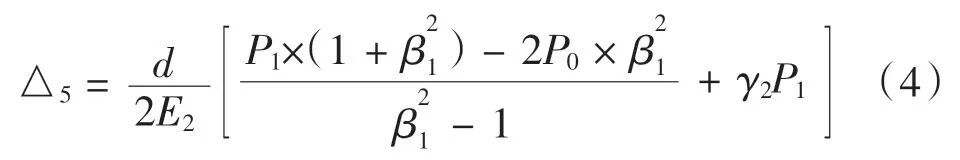
其中,P0為收縮盤內(nèi)外環(huán)之間的接觸壓強(qiáng),P1為收縮盤內(nèi)環(huán)與行星架之間的接觸壓強(qiáng),β1= dave/d。
行星架外徑的位移量:
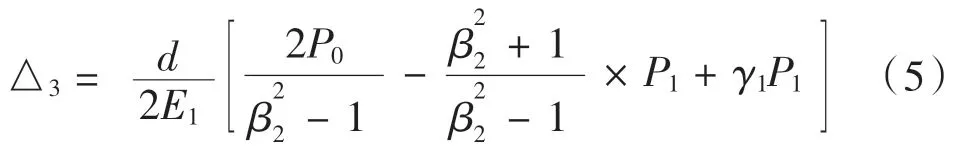
行星架內(nèi)徑的位移量:
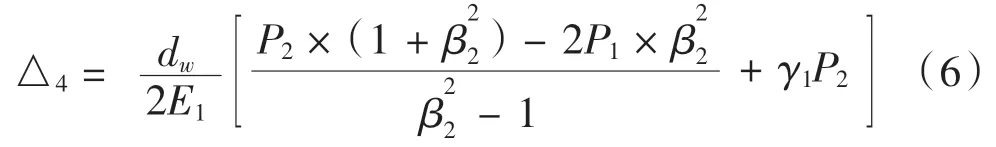
其中P2為行星架與主軸之間的接觸壓強(qiáng),β2=d/dw。
主軸外徑的位移量:
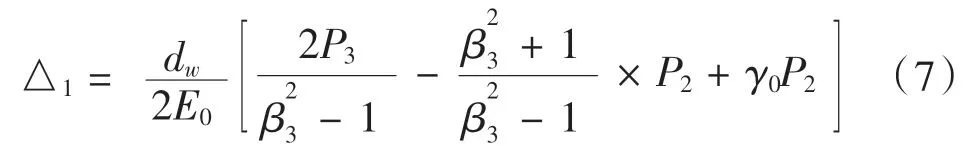
主軸內(nèi)徑的位移量:
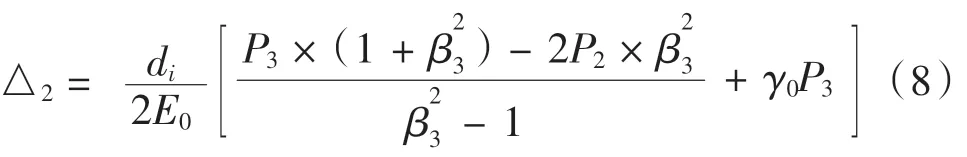
其中,P3為主軸與鋼套之間的接觸壓強(qiáng),β3=dw/di。
鋼套外徑的位移量:
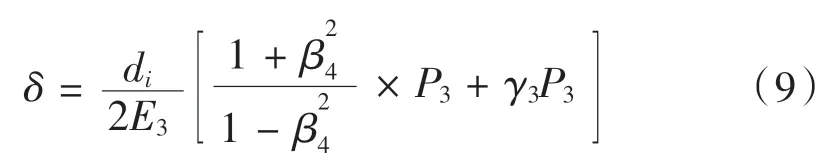
其中,β4= di/dg。
收縮盤內(nèi)外環(huán)之間的接觸壓強(qiáng)P0為:
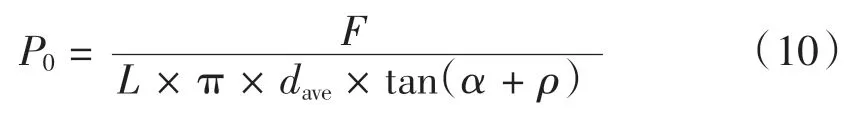
其中F 為脹緊套螺栓的預(yù)緊力,收縮盤的長(zhǎng)度L=370 mm,dave= 993.3 mm,收縮盤斜面角 α = 2.7°,摩擦角 ρ = arctan0.045 = 2.58°。
已知應(yīng)力測(cè)量試驗(yàn)時(shí),采用液壓拉伸器分四次按照十字交叉法擰緊螺栓,每次擰緊時(shí)增加1/4 的螺栓額定預(yù)緊力(具體見(jiàn)第4 部分)。試驗(yàn)中會(huì)分別記錄第二次和最后一次螺栓擰緊時(shí)液壓拉伸器的壓力和應(yīng)變片的數(shù)據(jù)。為方便表述,將第二次螺栓擰緊時(shí)的工況稱為工況一,將最后一次螺栓完全擰緊后達(dá)到額定預(yù)緊力的工況稱為為工況二。根據(jù)記錄的液壓值計(jì)算得到的脹緊套螺栓預(yù)緊力分別為9 742.7 kN、 19567.1 kN。脹緊套各部件的材料性能如表1 所示,將螺栓預(yù)緊力代入,聯(lián)立公式(1)-(9),可得各表面的接觸壓強(qiáng),如表2 所示。

表2 各工況下的接觸壓強(qiáng)
將脹緊套各部件等效為厚壁圓筒模型,運(yùn)用拉梅方程來(lái)計(jì)算各部件內(nèi)外表面的應(yīng)力。以行星架為例分析其外徑處的應(yīng)力,行星架內(nèi)外徑分別受到P1、P2的擠壓應(yīng)力,則:
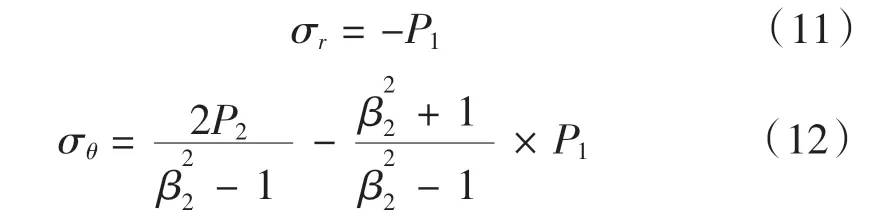
按照第四強(qiáng)度理論,等效應(yīng)力為:
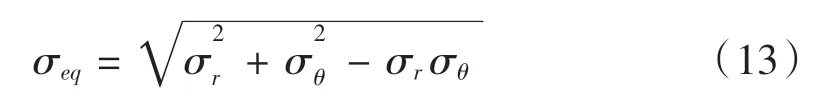
同理可得,各部件內(nèi)外徑處的應(yīng)力如表3 所示。
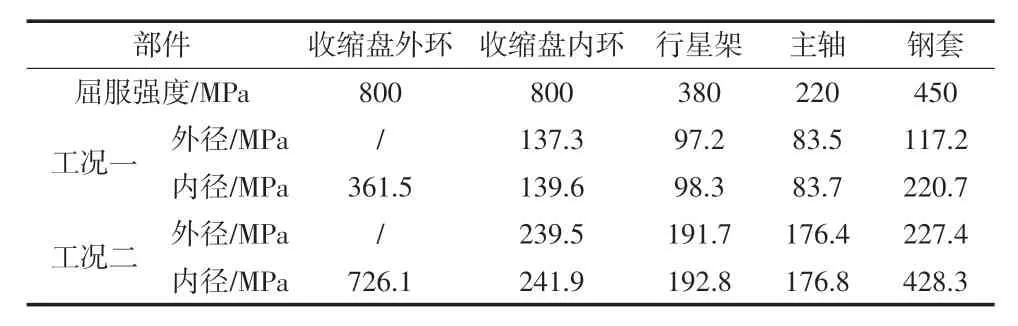
表3 各部件內(nèi)外徑的應(yīng)力值
由于主軸熱套時(shí)的高溫會(huì)使剛套內(nèi)表面應(yīng)變片的膠水失效,導(dǎo)致應(yīng)變片無(wú)法測(cè)得試驗(yàn)數(shù)據(jù),因此需在熱套后待主軸與剛套完全冷卻至室溫,才在剛套內(nèi)表面貼應(yīng)變片,所以應(yīng)變片測(cè)量的是剛套安裝后直至整個(gè)脹緊套安裝完成,螺栓按額定扭矩?cái)Q緊時(shí)的應(yīng)力變化。因此還需要計(jì)算主軸熱套鋼套后,鋼套內(nèi)徑處的應(yīng)力值。計(jì)算方法與前面一致,不再詳述,代入主軸內(nèi)徑與鋼套外徑之間的間隙△d2= -0.04 mm,計(jì)算可得鋼套內(nèi)徑處的應(yīng)力為24.5 MPa。則在工況一和工況二時(shí),鋼套內(nèi)徑處的應(yīng)力變量分別為196.2 MPa 和 403.8 MPa。
3 有限元仿真
按照前面理論計(jì)算的模型繪制三維模型,簡(jiǎn)化了脹緊套收縮盤內(nèi)外環(huán)之間的螺栓,模型如圖2 所示。各個(gè)接觸面的設(shè)置如表4 所示。將主軸大法蘭端面和行星架端面固定,限制收縮盤內(nèi)環(huán)的軸向位移,在收縮盤外環(huán)端面增加一個(gè)載荷傘,在loadpoint 分別施加脹緊套M33 螺栓的預(yù)緊力,有限元仿真的結(jié)果如圖3、圖4 所示。為了與試驗(yàn)結(jié)果作比較,測(cè)量鋼套內(nèi)經(jīng)貼應(yīng)變片處的應(yīng)力,結(jié)果如表5 所示。

圖2 有限元仿真模型
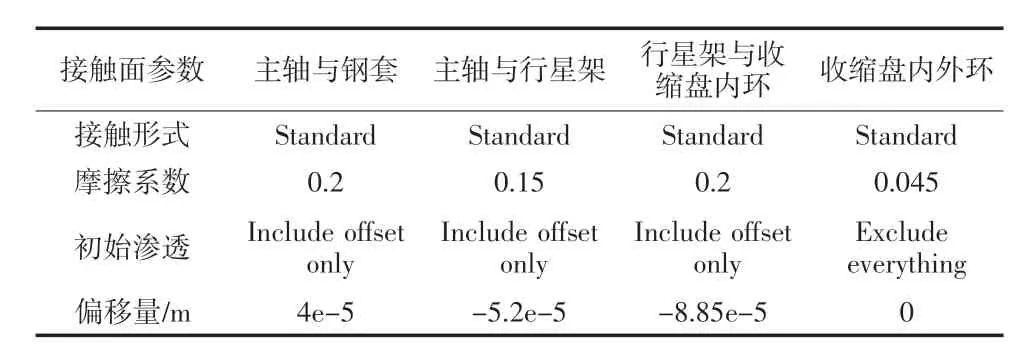
表4 接觸面參數(shù)設(shè)置
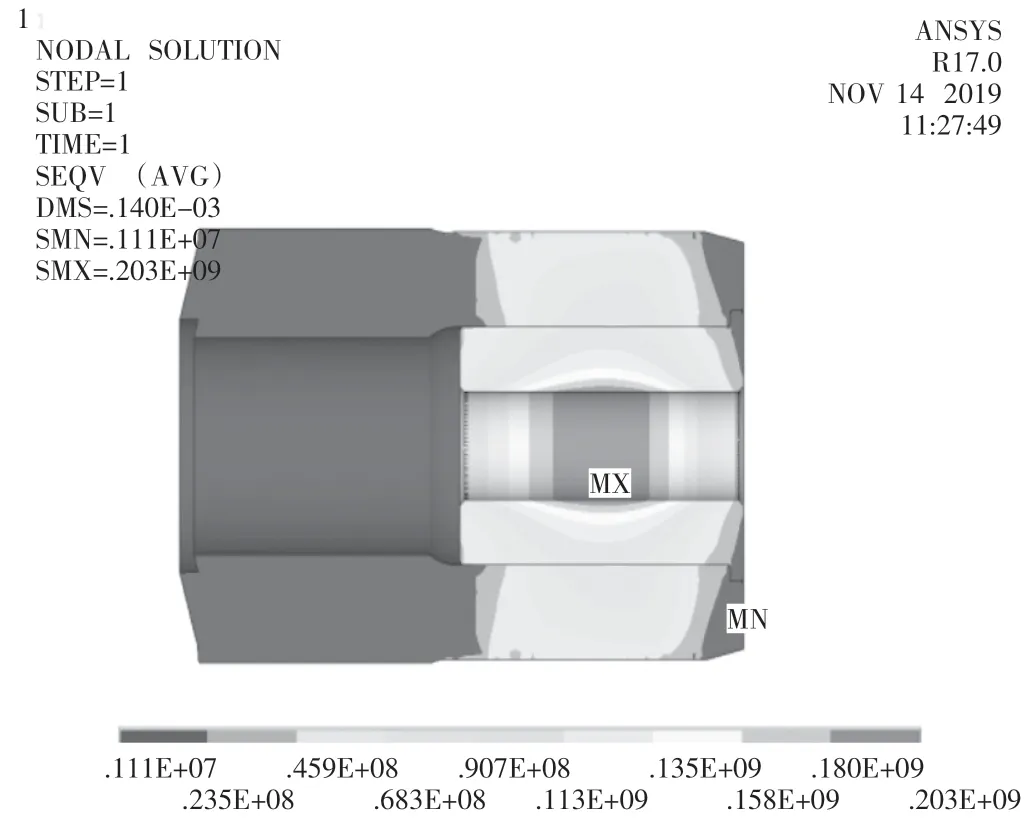
圖3 工況一時(shí)主軸鋼套的應(yīng)力圖
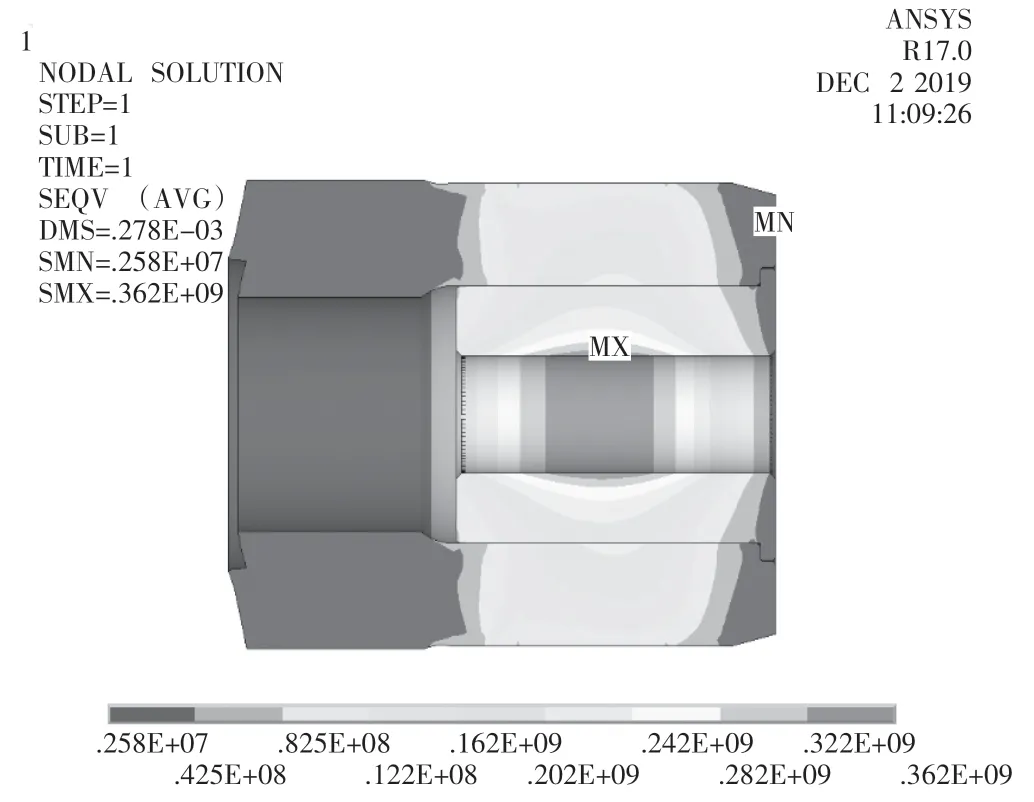
圖4 工況二時(shí)主軸鋼套的應(yīng)力圖

表5 鋼套內(nèi)側(cè)應(yīng)力最大值及應(yīng)變片出的應(yīng)力
有限元仿真的結(jié)果是脹緊套、主軸、鋼套共同作用的結(jié)果,為了與試驗(yàn)結(jié)果對(duì)比,還要減去鋼套熱套后鋼套內(nèi)徑處的應(yīng)力。建立主軸和鋼套的有限元模型,主軸大法蘭端固定,主軸與鋼套之間建立Standard 接觸,摩擦系數(shù)0.2,初始滲透Include offset only,偏移量4e-5m,結(jié)果如圖5 所示,測(cè)得貼應(yīng)變片處的應(yīng)力值為23.5 MPa。則工況一時(shí),鋼套內(nèi)徑貼應(yīng)變片處的應(yīng)力增量為159.1 MPa;工況二時(shí),鋼套內(nèi)徑貼應(yīng)變片處的應(yīng)力增量為276.4 MPa。

圖5 熱套后主軸剛套的應(yīng)力圖
4 應(yīng)力測(cè)量試驗(yàn)
為了獲得真實(shí)的應(yīng)力結(jié)果,脹緊套安裝前,在鋼套內(nèi)徑處貼了4 組應(yīng)變片,位置如圖1 所示,在距離主軸小端面200 mm 處,沿內(nèi)壁周向均勻分布,應(yīng)變片安裝完后如圖6 所示。應(yīng)變片安裝完成后,記錄應(yīng)變片的應(yīng)變初始值。在脹緊套安裝到主軸上后,先按照額定扭矩的一半拉伸螺栓,記錄應(yīng)變片的應(yīng)變值;再按額定預(yù)緊力拉伸螺栓,記錄應(yīng)變片的應(yīng)變值。應(yīng)變片的測(cè)量結(jié)果如表6 所示。已知鋼套的材料為34CrNiMo6,彈性模量 E = 2.1 × 105 MPa,則工況一時(shí),4 組應(yīng)變片的平均應(yīng)變量為1 145.103 μm/m,應(yīng)力增量為240.5 MPa;工況二時(shí),4 組應(yīng)變片的平均應(yīng)變量為1 262.427 μm/m,應(yīng)力增量為265.1 MPa。

圖6 應(yīng)變片安裝示意圖
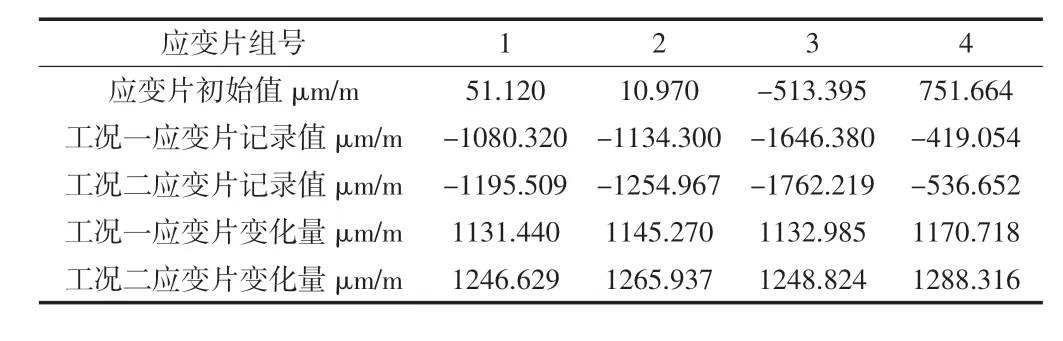
表6 應(yīng)變片數(shù)據(jù)記錄表
5 結(jié)果對(duì)比
應(yīng)力測(cè)量得到的結(jié)果與理論計(jì)算、 有限元仿真對(duì)比如表7 所示。工況一時(shí),無(wú)論是理論計(jì)算還是有限元仿真,與試驗(yàn)得到的結(jié)果都相差較大。工況二時(shí),理論計(jì)算的應(yīng)力值要比實(shí)際測(cè)得的應(yīng)力值大52.3%,而有限元仿真的結(jié)果與試驗(yàn)測(cè)得結(jié)果非常接近,當(dāng)按照額定扭矩?cái)Q緊螺栓之后,兩者的偏差只有4.3%。經(jīng)過(guò)分析,收縮盤內(nèi)外環(huán)之間的摩擦系數(shù)0.045 遠(yuǎn)大于實(shí)際的摩擦系數(shù),經(jīng)過(guò)與脹緊套廠家的交流,實(shí)際摩擦系數(shù)約為0.01。將收縮盤內(nèi)外環(huán)之間的摩擦系數(shù)設(shè)置為0.01,則根據(jù)拉梅方程理論計(jì)算后可得剛套內(nèi)側(cè)的應(yīng)力為347.4 MPa,除去剛套熱套后的應(yīng)力增量24.5 MPa,實(shí)際應(yīng)力增量為322.9 MPa。更改有限元模型中收縮盤內(nèi)外環(huán)之間的摩擦系數(shù)為0.01,則有限元仿真結(jié)果如圖7 所示,應(yīng)變片處的應(yīng)力為268.2 MPa,除去剛套熱套后的應(yīng)力增量23.5 MPa,則實(shí)際應(yīng)力增量為244.7 MPa。工況二時(shí),理論計(jì)算得到的剛套內(nèi)側(cè)應(yīng)力增量為658.1 MPa,有限元仿真剛套內(nèi)側(cè)應(yīng)變片處的應(yīng)力增量為275.8 MPa,如圖8 所示。修改摩擦系數(shù)為0.01 后應(yīng)力測(cè)量得到的結(jié)果與理論計(jì)算、 有限元仿真對(duì)比如表8 所示,從表中可以看出,此時(shí)理論計(jì)算的結(jié)果與試驗(yàn)結(jié)果依然相差甚遠(yuǎn),兩個(gè)工況的偏差分別達(dá)到了34.2%和148.2%;有限元仿真的結(jié)果與試驗(yàn)測(cè)得結(jié)果非常接近,兩個(gè)工況的偏差分別為1.7%和4.0%。從理論計(jì)算、有限元仿真與試驗(yàn)結(jié)果的對(duì)比來(lái)看,主要有以下結(jié)論:首先收縮盤內(nèi)外環(huán)之間的實(shí)際摩擦系數(shù)遠(yuǎn)小于0.045;其次,運(yùn)用拉梅方程理論計(jì)算的過(guò)程中,做了很多的簡(jiǎn)化,例如未考慮各接觸面的邊緣效應(yīng),未考慮止口的作用等,導(dǎo)致理論計(jì)算結(jié)果與實(shí)際偏差很大,而有限元仿真能夠更真實(shí)的模擬脹緊套安裝的實(shí)際情況,獲得的結(jié)果也與實(shí)際相符。實(shí)際中更應(yīng)優(yōu)先采用有限元方法指導(dǎo)其安裝優(yōu)化。
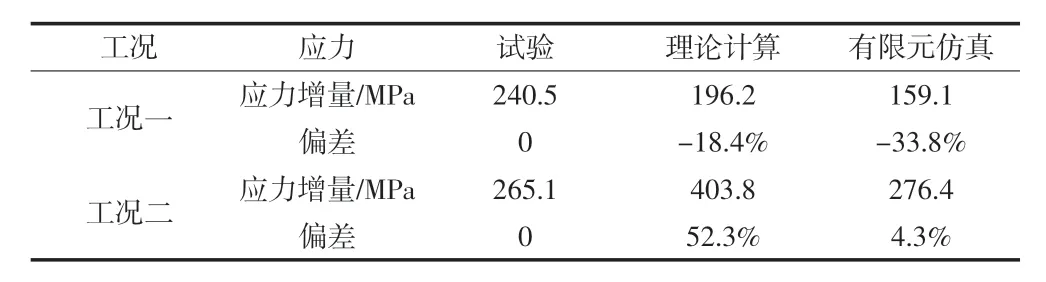
表7 應(yīng)力測(cè)量結(jié)果與拉梅方程、有限元仿真結(jié)果對(duì)比
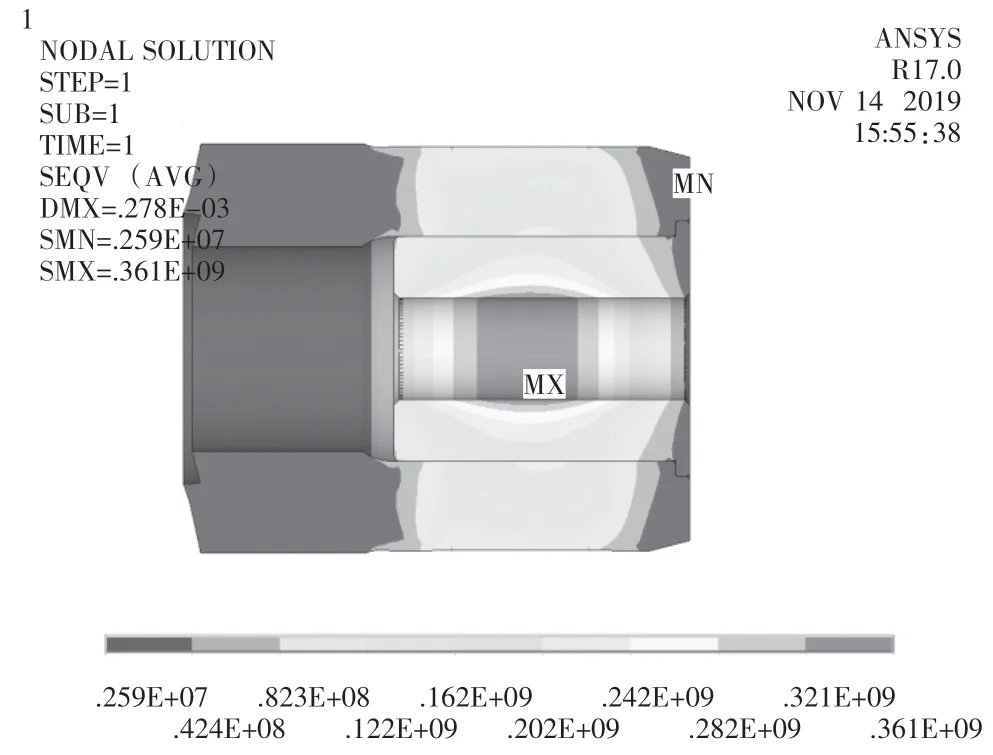
圖7 工況一收縮盤內(nèi)外環(huán)摩擦系數(shù)為0.01 時(shí)主軸剛套的應(yīng)力圖
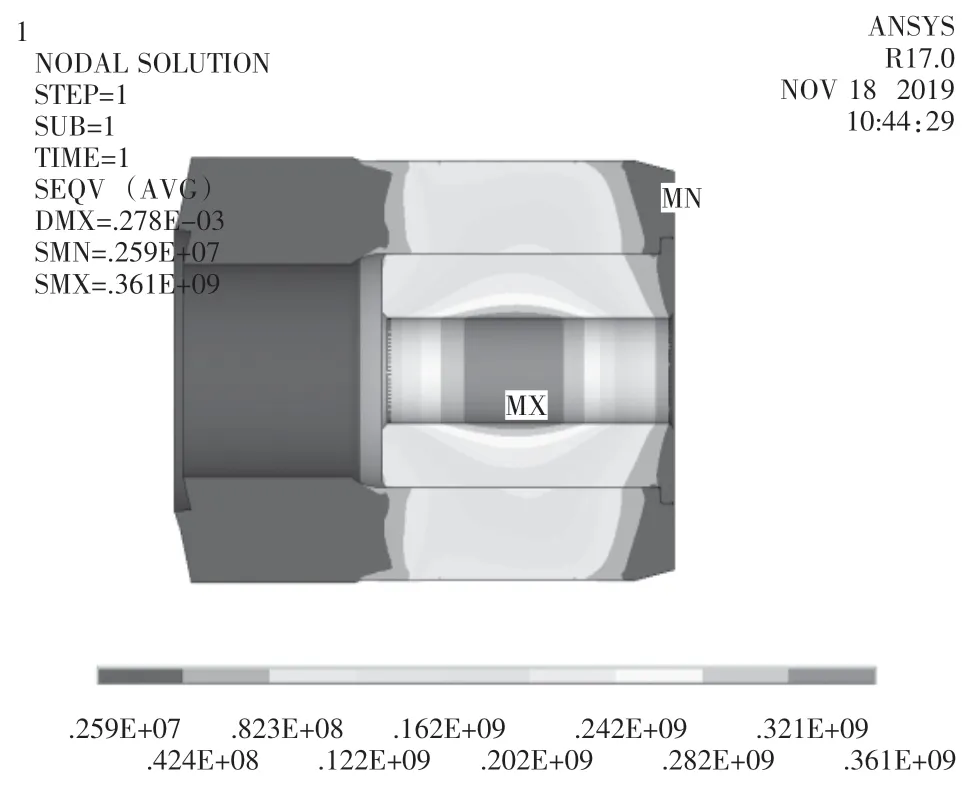
圖8 工況二收縮盤內(nèi)外環(huán)摩擦系數(shù)為0.01 時(shí)主軸剛套的應(yīng)力圖
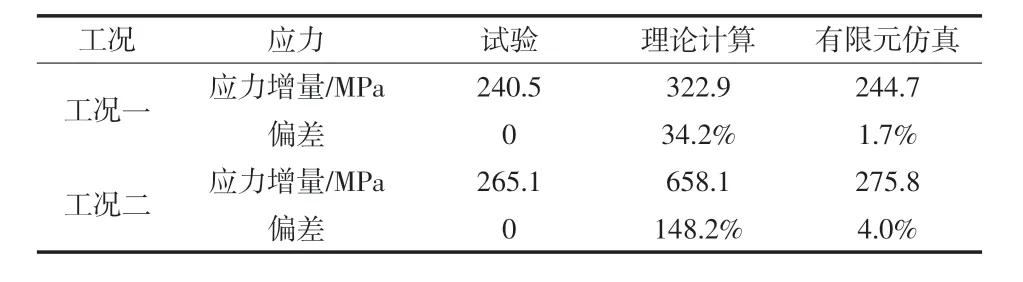
表8 收縮盤內(nèi)外環(huán)摩擦系數(shù)為0.01 時(shí)應(yīng)力測(cè)量結(jié)果與拉梅方程、有限元仿真結(jié)果對(duì)比
6 結(jié)束語(yǔ)
本文分別通過(guò)拉梅方程、有限元仿真,對(duì)風(fēng)力發(fā)電機(jī)組鑄造主軸尾端與齒輪箱脹緊套聯(lián)接部分的強(qiáng)度進(jìn)行分析,并與試驗(yàn)測(cè)得的結(jié)果進(jìn)行對(duì)比,有限元仿真能夠更好地模擬主軸和脹緊套的實(shí)際應(yīng)力,實(shí)際中更應(yīng)優(yōu)先采用有限元方法為主軸和脹緊套強(qiáng)度校核。

