電子型FeSe基高溫超導體的磁通束縛態與Majorana零能模*

陳晨 劉琴2) 張童3)5)? 封東來

1) (復旦大學物理學系,應用表面物理國家重點實驗室,先進材料實驗室,上海 200438)

2) (表面物理與化學重點實驗室,綿陽 621908)

3) (人工微結構科學與技術協同創新中心,南京 210093)

4) (中國科學技術大學物理學院,合肥微尺度物質科學國家研究中心,合肥 230026)

5) (上海量子科學研究中心,上海 201315)

作為凝聚態物理中一類新奇準粒子態,Majorana零能模(Majorana zero mode)由于可用來實現拓撲量子計算而成為當前的研究熱點.理論預言,Majorana零能模可作為特殊的束縛態出現在一些拓撲超導體的磁通渦旋中.但實際超導體磁通中還可能存在其他低能束縛態或雜質態,這給Majorana零能模的辨別和具體應用帶來了困難.目前實驗上尋找合適的拓撲超導體系、分辨出清晰的Majorana零能模仍然是十分迫切的.本文主要介紹最近利用高能量分辨的掃描隧道顯微鏡,對電子摻雜鐵硒類超導體(Li,Fe)OHFeSe和單層FeSe/SrTiO3磁通態進行的研究.實驗上在前者的自由磁通中觀測到清晰的零能模,并進一步測量到Majorana零能模的重要特征—量子化電導.而在后者磁通中只發現常規Caroli-de Gennes-Matricon (CdGM)束縛態,反映出s波對稱性的特征.這系列實驗既為Majorana零能模物性的進一步研究提供了合適平臺,也為澄清鐵基超導體中拓撲超導電性的來源提供了線索.

1 引 言

超導電性是由其序參量(Δk)描述的宏觀量子現象.對第二類超導體,磁場可以部分穿過超導內部形成量子化的磁通渦旋,并可呈晶格狀排列(圖1(a)和圖1(b)).渦旋中心處的超導序參量為零,隨著距離的遠離逐漸恢復到正常值,因此形成超導準粒子的“勢阱”.1964 年,Caroli等[1]發現對于 s波超導體 (Δk=Δ),求解 BdG 方程可得到磁通中存在準粒子束縛態,稱為 Caroli—de Gennes-Matricon (Cd-GM)束縛態.這些態具有離散的能級,低能近似表達式為Eμ=μΔ2/EF.其中系數μ是與軌道角動量相關的量子數,這里取值為半整數 (± 1/2,± 3/2,··),EF是費米能級.可看出磁通態能級關于費米面對稱分布但沒有零能態.

20 世紀末,Volovik[2],Read 和 Green[3]等發現對于手性 p 波的超導體 (Δk=Δ(kx+ iky))或者超流體,其渦旋中心的束縛態能級仍可寫為Eμ=μΔ2/EF,但角動量量子數μ變為整數 (0,± 1,± 2,··).這是因為其特殊的序參量產生額外的相位,改變了渦旋中準粒子波函數邊界條件.而能量E= 0的束縛態即為 Majorana 零能模 (Majorana zero mode).Majorana零能模是凝聚態物質中的一類特殊準粒子態[4-8],它可看作由粒子和空穴態混合而成,其反粒子為其自身.重要的是它是滿足非Abelian統計的最簡單準粒子態,可用于構建拓撲量子比特,實現容錯型拓撲量子計算[9,10].進一步理論還指出,Majorana零能模的出現是超導體系具有拓撲非平庸性的直接體現： 它是拓撲超導體的一種邊界態.而上述手性p波超導體就是一種拓撲超導體.

圖1 超導體磁通束縛態 (a) 磁通渦旋的示意圖； (b) NbSe2 的磁通晶格圖像[22]； (c)理論計算的 s波超導體分立的磁通束縛態及其空間分布[24]； (d) 實驗測量的NbSe2從磁通中心向外的微分電導譜[23]； (e) 理論計算的拓撲超導體磁通態和空間、自旋分布情況[44]； (f) 5層Bi2Te3/NbSe2異質結的磁通的微分電導譜[14],零能模在磁通中心一段距離內都存在Fig.1.Bound states in the vortex core of superconductor： (a) Sketch of a magnetic vortex (b) vortex lattice measured on NbSe2；(c) calculated discrete bound states near the vortex core of s-wave superconductor； (d) a seris of spectra measured near the vortex center of NbSe2； (e) wave functions of several low-energy quasiparticle excitations in a vortex of topological superconductor； (f) color plot of a set of dI/dV spectra measured along the vortex core on 5 QL Bi2Te3/NbSe2 heterostruture.Majorana zero mode exists within a certain distance near the vortex center.

Majorana零能模的潛在應用價值極大激發了人們對拓撲超導還有它們邊界態的研究.但在實驗上p波超導十分不易實現,尤其對自旋簡并p波超導還需要半整數磁通才能得到單個Majorana零能模[2].直到2008年,麻省理工學院的Fu和Kane[11]提出了一種易于實現的模型體系,即讓s波超導體和自旋手性的拓撲表面態耦合在一起,則該體系的哈密頓量等效于無自旋的手性p+ ip波超導體,其磁通中心即可觀測到單個Majorana零能模.后來該模型也被拓展到一維體系[4-7].基于這一設想的實驗迅速展開,目前人們已在s波超導/拓撲絕緣體薄膜異質結[12-15],一維鏈狀系統(半導體納米線、磁性鏈)與超導體耦合體系[16-20]中觀察到許多Majorana零能模的重要跡象.

本文主要關注超導磁通渦旋中的Majorana零能模.如前所述,磁通束縛態的研究很早就已開始,要檢驗Majorana零能模,首先要看這些磁通態中有無零能態.掃描隧道顯微鏡(STM)因為具有探測局域電子態的能力并可在極低溫下工作,因此很適合測量磁通束縛態[21].但長期以來人們并未在超導磁通中看到分立的束縛態能級,這主要是因為磁通態之間的能量間隔通常太小了.比如對一般金屬或合金超導體,Δ的典型值約 1 meV,而EF≈1 eV,則能量間隔Δ2/EF僅為 1 μeV,這遠小于目前最低溫度STM的能量分辨率.另外如果體系存在雜質散射等其他因素,則能級會被展寬而變得更難分辨.例如Hess等[22,23]在NbSe2磁通中心只觀察到一個很寬的零偏壓峰,并且遠離磁通中心時,這一零偏壓峰開始劈裂(見圖1(d)).而離散磁通態的行為理論上如圖1(c)所示： 低能磁通態的能量不隨距離變化但強度隨距離指數衰減(同時疊加一個周期為費米波長的振蕩).當μ較大時,高能級束縛態Eμ在距離rμ～|μ|/kF處有最大的強度[24].因此NbSe2磁通中看到的零偏壓峰和劈裂的峰實際上是一系列磁通態的包絡,并且許多其他超導體中看到的都是類似現象[25-27].

近年來,鐵基高溫超導的出現給磁通束縛態乃至拓撲超導研究提供了新的契機.此類材料能帶較窄,具有小EF和相對大的、完全打開的超導能隙,因此有利于磁通束縛態的觀測.并且理論上許多鐵基超導體可以存在拓撲非平庸的電子結構[28-31].最近人們在Fe(Te,Se)觀測到分立的磁通束縛態和零能模[32-35],還觀測到自旋手性的表面態,并且有來自體態近鄰效應的超導能隙[36].這意味著Fe(Te,Se)是符合Fu-Kane模型的拓撲超導系統.由于磁通之間的相互作用[37]和材料局域組分不均勻[35]等因素,實驗上只在一定比例的磁通中探測到Majorana零能模.

上面的結果表明,要在磁通中尋找清晰的Majorana零能模,需要材料體系盡量滿足：

1)是本征拓撲超導體或者擁有拓撲非平庸的電子結構,符合Fu-Kane模型；

2)較小的EF和盡量大的超導能隙(也即較高的Tc),這既有利于測量也有利于增強Majorana零能模抗干擾能力；

3)較短的超導相干長度來減弱磁通間相互作用和磁通釘扎；

4)化學配比均勻的超導層來避免局域無序和雜質帶來的干擾.

同時需要指出的是,零偏壓電導峰并不一定就來源于Majorana零能模,許多其他效應也可產生零能峰(或很靠近零能的峰),比如雜質束縛態(Yu-Shiba-Rusinov 態)[38],Kondo 效應[39],SIS 隧穿[40]等.因此實驗上一方面要排除這些平庸零能態的出現,另一方面還要檢驗觀測到的零能峰是否具有Majorana零能模的其他重要特征,比如電導量子化[20,41,42]和自旋極化[15,19,43-45]等.與此同時,對比研究不同能帶結構的鐵基超導體磁通態對理解其產生機理也有幫助.

本文將介紹最近對電子摻雜鐵硒類超導體(Li,Fe)OHFeSe和單層FeSe/SrTiO3磁通態進行的研究[46-48].實驗發現前者具有清晰和“魯棒”的零能模而且表現出Majorana零能模的特征—量子化的電導,而后者只具有常規CdGM磁通態,是s波對稱性的表現.全文結構如下,第2節介紹(Li,Fe)OHFeSe體系的能帶計算和光電子能譜測量； 第3節介紹(Li,Fe)OHFeSe無釘扎磁通的STM測量； 第4節介紹利用更高能量分辨STM對(Li,Fe)OHFeSe零能模的量子化電導測量； 第5節介紹單層FeSe/SrTiO3薄膜的磁通態的對比實驗結果； 第6節是全文的總結與對未來的展望.

2 (Li,Fe)OHFeSe 的能帶結構與光電子能譜測量

鐵基超導是多帶體系,成員眾多且具有豐富的物性.2014年Hao和Hu[28]就預言鐵基超導中可存在拓撲非平庸的能帶結構,隨后在Fe(Se,Te)材料的計算中得到進一步發展[29,30].(Li,Fe)OHFeSe是近年來發現的插層類重電子摻雜FeSe基超導體[49-52],Tc達到 42 K,其晶體結構如圖2(a)所示.文獻[46]采用密度泛函理論(DFT)結合動態平均場理論(DMFT)[53,54]計算了(Li0.75Fe0.25)OHFeSe的能帶結構,發現其也具有滿足Fu-Kane模型的拓撲表面態與拓撲非平庸的體能帶.

圖2 (Li,Fe)OHFeSe 的能帶結構和拓撲表面態 (a) (Li,Fe)OHFeSe 的晶體結構、體態和 (001)表面的布里淵區； (b)利用DFT+DMFT計算的(Li0.75Fe0.25)OHFeSe沿著M-Γ-Z-(R)方向的能帶結構； (c)沿 方向在(001)面上計算的體態和狄拉克錐狀的拓撲表面態； (d) LiOHFeSe在無自旋軌道耦合且處于順磁PM狀態下的能帶結構Fig.2.Band structure and topological surface states of (Li,Fe)OHFeSe： (a) The crystal structure and bulk & (001) surface Brillouin zone of (Li,Fe)OHFeSe； (b) band structure of (Li0.75Fe0.25)OHFeSe along M-Γ-Z-(R) direction,represented by spectral functions calculated by density functional theory (DFT) combined with dynamical mean-field theory (DMFT) methods； (c) calculated bulk and Dirac-cone-like topological surface states on the (001) surface along the direction； (d) band structure of LiOHFeSe in the PM state without spin orbital coupling (SOC).

如圖2(b)所示,(Li0.75Fe0.25)OHFeSe沿Γ-Z方向的費米面附近存在三條較平的能帶和一條有明顯色散的能帶,前者主要是Fe的3dxy,3dyz和3dxz軌道所貢獻,而后者主要由Se的4pz軌道和(Li,Fe)OH層中Fe原子的3dz2軌道所組成.該具有色散的能帶在Γ點和Z點是奇宇稱,并且它穿越了費米能級和Fe的3d能帶,形成了拓撲非平庸的能帶反轉.這里(Li,Fe)OH層中的Fe原子起到了很重要的作用,它和Se的4pz軌道發生了很強的雜化,因而改變了Se的4pz能帶的色散和位置.

此外,材料中的自旋軌道耦合具有非常大的作用.如果沒有自旋軌道耦合,Fe 的 3dxz和 3dyz能帶在Γ點處是簡并的,處于態,而色散的Se的4pz能帶在Γ點處是奇宇稱的態.存在自旋軌道耦合時,雙簡并的態分為一個低能的態和一個高能的態,并且態變為態[29].在四方晶體結構固有的C4v對稱性下,這兩個態和態衍生出 Λ6能帶,主要是 Fe的 3dxz和Se的4pz軌道,且沿著Γ-Z方向發生雜化,并在它們的交叉點附近(圖2(b)中的虛線圓圈處)打開一個約2.5 meV的能隙.在自旋軌道耦合能隙打開后,可計算體系的Z2不變量為 1[29],這表明(Li0.75Fe0.25)OHFeSe處于拓撲非平庸相,會在體能隙中出現無能隙拓撲表面態,表面的不連續性消除了態和態之間的雜化能隙.進一步計算表明點處的狄拉克錐狀的表面態出現在(001)表面上,如圖2(c)所示.拓撲表面態具有螺旋自旋結構,當它由體態超導近鄰效應而變得超導時,可在磁通中心產生Majorana零能模[11].

作為對比,圖2(d)給出了相同晶體結構但LiOH層中沒有摻雜Fe原子的LiOHFeSe的能帶結構.可以看出在費米能級附近,LiOHFeSe的三條 Fe 3d 能帶與 (Li0.75Fe0.25)OHFeSe相似,而不同的地方在于它沒有Se pz能帶穿越費米能級與Fe的3d能帶相交,這表明沿Γ-Z方向沒有出現拓撲能帶反轉.因此LiOHFeSe是拓撲平庸的.綜上所述,LiOH層中的鐵原子在誘導(Li,Fe)OHFeSe的非平庸能帶拓撲及其(001)表面的拓撲表面態方面起著重要作用.

為了驗證理論計算中的能帶結構,實驗上對(Li,Fe)OHFeSe材料進行了角分辨光電子能譜(angle resolved photo-emission spectroscopy,ARPES)的測量.測量樣品是LaAlO3襯底上通過基體輔助水熱外延技術生長的高質量的(Li0.84Fe0.16)OHFeSe單晶薄膜[55,56],超導轉變溫度Tc≈ 42 K.圖3(a)給出了其布里淵區中心點附近的光電子譜圖.可以看到費米能量以下有多條拋物線能帶,且在—300 meV附近有一個平坦帶.此外在點處觀察到一條帶底在—50 meV的電子能帶(圖3(g)和圖3(h)).這些觀測到的能帶和圖2(b)中計算的能帶定性上有一一對應的關系.但由于電子關聯效應,能帶絕對位置和帶寬與理論有所不同.還有些計算中的能帶沒有被觀測到(比如點處的其他電子能帶).但圖2(b)中的計算還是定性反映了能帶的特征,并且與其他一些鐵硫族超導體類似[57].需要指出的是重電子摻雜FeSe體系的精確能帶計算至今仍然是有挑戰性的.

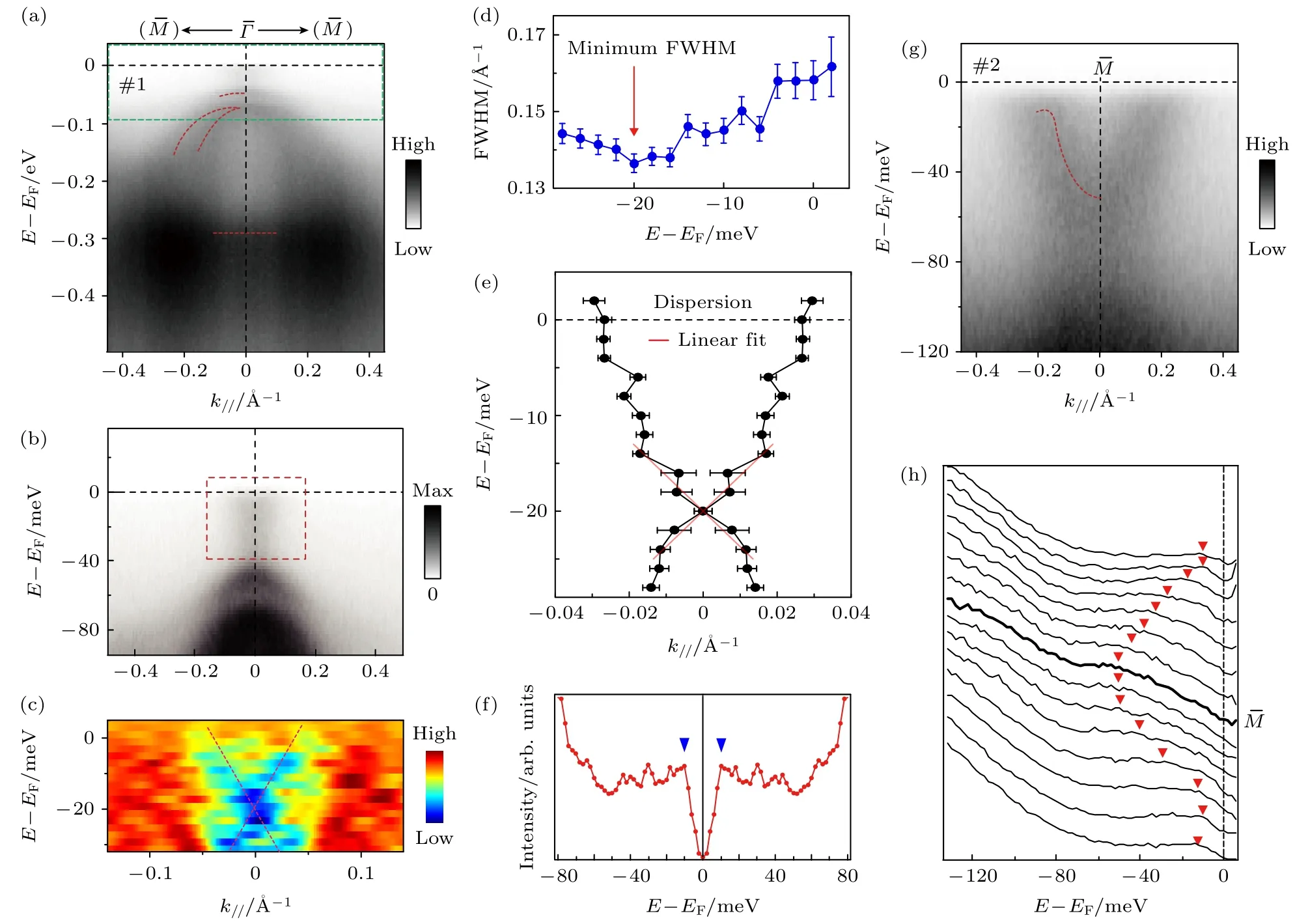
圖3 (Li0.84Fe0.16)OHFeSe 的角分辨光電子實驗測量 (a) 沿著圖2(a)中切割線#1 的方向穿過 點測量的光電子能譜； (b) 在圖(a)中 點費米能量附近綠色虛線框中放大的數據； (c) 圖(b)紅色虛線框區域的光電子能譜的二階導數,可以看到類似狄拉克錐的色散； (d) 擬合得到的作為能量函數的峰的半高寬； (e)從數據中提取的E-k色散以及交叉點處的線性擬合； (f) 點電子口袋附近的對稱化的能量分布曲線,可以觀察到約10 meV的超導能隙； (g) 沿圖2(a)中切割線#2穿過 點的光電子能譜；(h) 圖(d)中數據除以費米-狄拉克分布后的能量分布曲線(EDCs).所有數據均在5.6 K溫度下用21.2 eV能量的光子測量Fig.3.ARPES measurement of (Li0.84Fe0.16)OHFeSe： (a) Photoemission intensity across along cut #1 in Fig.2(a)； (b) an enlargement of data corresponds to the green dashed rectangle in panel (a) near EF at point； (c) second derivative of the photoemission intensity in the marked region of panel (b),a Dirac-cone like dispersion can be seen； (d) the FWHM obtained from fitting,as a function of energy； (e) E-k dispersion extracted from the data,and the linear fit around the crossing point； (f) symmetrized energy distribution curve (EDC) near the Fermi crossing of the M pocket,where a superconducting gap of ～10 meV is observed；(g) photoemission intensity taken along cut #2 across in Fig.2(a)； (h) the energy distribution curves (EDCs) of the data in panel (d) after dividing by Fermi-Dirac distribution.All the data were measured at 5.6 K using 21.2 eV photons.

3 (Li,Fe)OHFeSe 的磁通束縛態測量

為了探測 (Li,Fe)OHFeSe 的磁通態,實驗采用了極低溫STM進行測量(本節數據均在400 mK溫度下測得,系統等效電子溫度Teff= 1.18 K).圖4(a)是樣品解理后的表面形貌,可看到FeSe和(Li,Fe)OH兩種不同的表面終止面.圖4(b)給出了FeSe面上典型的超導能隙譜(藍色線),它具有兩對超導相干峰(Δ1和Δ2)和U型底部,與單晶樣品中報道的一致[58].而(Li,Fe)OH終止面的隧道譜表現出金屬性(圖4(b)中的綠色線),無超導能隙.因為能帶計算和ARPES實驗表明FeSe面上可能有拓撲表面態,因此STM觀測到的雙能隙可能分別來源于體態和表面態.利用各向異性能隙 函 數Δ(k)=Δmin+(Δmax-Δmin)|cos(2θk)|,可分別擬合這兩個能隙的大小(Δmax,Δmin分別為能隙最大和最小值).此外FeSe面上存在“啞鈴”狀缺陷,可能是Fe空位或替換雜質.它們可在超導能隙內產生明顯的雜質態.

圖4 (Li0.84Fe0.16)OHFeSe樣品的形貌、超導能隙、準粒子干涉和磁通束縛態 (a)解理后樣品表面的形貌圖,右下插圖是FeSe 面原子晶格 (晶格常數 a0 = 3.8 ?).虛線圓圈內是啞鈴狀雜質； (b) FeSe 和 (Li,Fe)OH 面的微分電導 dI/dV 譜； (c)利用QPI測量的 點電子型能帶的色散,虛線是拋物線擬合； (d) FeSe 面,B = 10 T 下的零偏壓電導成像.釘扎的磁通用箭頭標記,白色圓圈處是“自由”磁通； (e) 穿過自由磁通1的一系列隧道譜,可清晰看到磁通中心附近分立的束縛態； (f)對應圖(e)中隧道譜的顏色圖表示,箭頭標出了分立的磁通態； (g) 磁通中心附近較小范圍內的隧道譜,可看出零能峰的位置保持不變Fig.4.Topography,superconducting gap,QPI and vortex bound states of (Li0.84Fe0.16)OHFeSe： (a) Topographic image of a cleaved film.Inset： the lattice of FeSe surface (a0 = 3.8 ?).A dimer-like defect is marked by the circle； (b) typical dI/dV spectra taken on FeSe and (Li0.84Fe0.16)OH surface； (c) electron-like Energy dispersion measured by QPI at point.Dashed curve is a parabolic fit；(d) zero bias conductance map on FeSe surface under B = 10 T.Pinned-vortices are indicated by arrows.The dashed circle encloses a free vortex； (e) dI/dV spectra taken across the free Vortex 1 and discrete low-energy states were observed in the vortex core； (f) color plot of the spatial dependence of the dI/dV spectra shown in panels (e) and arrows indicate the positions of discrete vortex states； (g) dI/dV spectra taken at the small range near the vortex and the zero-bias peak keeps unchanged.

圖4(e)給出了0.4 K下測量的跨過自由磁通中心的隧道譜.在磁通中心附近可以清晰地觀測到5個分立的峰,且中間的峰剛好處在零偏壓處!而其余的峰則對稱地分布在兩側(能量間隔約為1.5 meV).需要指出的是在 STM 測量中,加在樣品上的實際偏壓值往往與設定值有meV量級的偏差,這里已經通過測量不同隧穿勢壘下的I-V曲線修正了偏壓的零點(圖5(f)).圖4(f)是相應譜的空間演化的彩色示意圖.此處將5個峰分別標記為E0,E±1,E±2.可以看出當遠離磁通中心時,低能分立束縛態的強度不斷減弱并消失.之后一對更為展寬的峰在高能量位置處出現(如圖4(e)中的陰影區域所示).這些峰在遠離磁通中心的過程中逐漸移向更高能量位置,形成了“X”型的形狀.

類似的分立磁通束縛態,包括零偏壓峰,在其他自由磁通中心都可被重復觀測到.圖5(a)—圖5(d)給出了四個不同磁通上測量的數據.而在不加磁場時,這些磁通所在的區域都具有清晰的U型超導能隙(圖5(e)),這排除了這些峰來源于雜質態的可能.在以往的測量中,分立的磁通束縛態很少被觀測到,這是因為一般常規超導體的能級間隔δE=Δ2/EF太小.而對于 (Li0.84Fe0.16)OHFeSe,由Δ≈10 meV,EF≈ 57 meV,可估算其 δE=Δ2/EF約1—2 meV,因此可以被低溫STM所分辨(實驗所用STM分辨率為0.36 meV).上述形成X形狀向外移動的峰,其實是來源于能量間隔變小的高能級磁通態的包絡,正如同在NbSe2等樣品中觀察到的那樣[22,23].因此實驗中同時觀測到了分立的低能束縛態和準連續的高能磁通態,這得益于(Li,Fe)OHFeSe較大的能級間隔δE和足夠高的STM能量分辨率.

圖5 磁通束縛態的定量特性 (a)—(d) 四個不同磁通中心的微分電導譜,紅色實線是多高斯函數擬合,虛線為每個高斯函數對應的峰； (e) 磁通1—4出現區域的局域超導能隙.最下方是磁通1對稱化后的dI/dV譜(藍色曲線)和各向異性能隙函數擬合(紅色曲線)； (f) 通過不同隧穿勢壘下的 I-V 譜對隧道譜零偏壓點的標定； (g) 能量|E2|,|E1|分別以 ( )2,(Δ2max)2 作為變量得到的擬合結果,其中虛線代表線性擬合的結果Fig.5.Quantitative characterization of the vortex core states： (a)—(d) Summed low-energy dI/dV spectra taken near the centers of Vortex 1—4.Red solid curves are the fits to multiple Gaussian peaks (dashed curves are the individual peaks)； (e) local superconducting gaps measured where Vortex 1—4 emerge.The bottom curves are the symmetrized dI/dV spectrum (blue one) for vortex 1 after subtracting a background slope and corresponding fit (red one) using anisotropic gap function； (f) calibration for the zero bias offset using a set of I-V spectra taken at different setpoints； (g) plots of (red circles) as a function of ( )2,and(blue circles) as a function of.Dashed lines are the linear fitting (see legend).

而零偏壓峰(E0)則是該實驗最主要的發現.比起其他高階峰,零能峰的峰位更穩定(不隨位置變化而移動,見圖4(f)和(g)),而且它的展寬也明顯小于其他峰,這顯示出其特殊的來源.通過對圖5(a)—圖5(d)中的峰位進行精確擬合可以得到更多的信息.首先,所有E0峰非常接近能量零點,其誤差均比系統的能量分辨率(0.36 meV)小一個量級.E0峰半高寬的范圍是 0.59—0.80 meV,因此它們有額外展寬約 0.23—0.44 meV.但無法把E0峰認為是兩個靠得很近的常規磁通態,因為如果按它們間隔為Δ2/EF來計算,相應的平均Δ大小約 3.6—5.0 meV(取EF= 57 meV),但這些磁通附近測得的局域超導能隙都遠大于這一數值(圖5(e)).因此,E0峰的最直觀解釋便是它來自于(Li0.84Fe0.16)OHFeSe的拓撲表面態.

第二點,對于不同的自由磁通,E±2和E±1這兩組峰的峰位是關于零點對稱的.但E2和E1之間的能級間隔總是略大于E1和E0之間的能級間隔(間隔之比 (E2—E—2)/(E1—E—1)在 2.1—2.5 之間).理論上對于單帶超導體,磁通態間隔會隨能級增加變小而非變大[24].因此這些峰可能來源于不同的能帶,并且隧道譜也確實觀察到雙能隙結構.但同時超導能隙的局域不均勻性和各向異性也會影響束縛態的能量.因此文獻[46]仔細測量了每個磁通所在區域的超導能隙并進行擬合(圖5(e)),發現較為可能的解釋是E0和E±2峰來自于表面態,而E±1峰來自于體態.擬合結果如圖5(g)所示.

另外通過指數擬合圖4(f)中E0峰強度隨遠離磁通中心的衰減,可得到其空間衰減長度為1.4 nm.這近似等于材料的超導相干長度(ξ).該ξ值遠小于B= 10 T 下磁通渦旋的平均間距 (約 14 nm),因此此時的磁通可認為是沒有相互重疊的(如果磁通有重疊或強相互作用,磁通束縛態能量將產生變化[37]).

最后對于被表面“啞鈴”缺陷釘扎的磁通,實驗上沒有觀察到零偏壓峰[46].由“啞鈴”缺陷可產生很強的能隙束縛態,并在磁場下顯示出劈裂行為,這些缺陷很可能局域地破壞了(Li0.84Fe0.16)OHFeSe的拓撲表面態從而壓制了零能模出現.這其中的具體機制還有待進一步研究.

自此(Li0.84Fe0.16)OHFeSe自由磁通中的分立磁通態得到了自洽解釋： 根據理論計算與ARPES測量,(Li0.84Fe0.16)OHFeSe具有拓撲非平庸能帶結構和拓撲表面態.手性的拓撲表面態通過體態近鄰效應變為超導后會在磁通中產生Majorana零能模,而體能帶也會產生其自身的CdGM磁通態,這些態疊加后形成隧道譜中觀察到的多個峰.當然,實驗上還需考慮其他可能的解釋.例如目前(Li,Fe)OHFeSe體態的超導配對對稱性還有爭議[58,60],因此文獻[46]針對不同的配對對稱性做了計算,結果發現如果不考慮拓撲表面態,則s波、d+id'波和無節點d波等對稱性均不會使磁通中產生零能峰.而其他可能導致隧道譜中出現零偏壓峰的效應,如Kondo效應、超導-絕緣體-超導隧穿等也可以被排除,因為自由磁通中沒有雜質,且此處的STM針尖是非超導的.因此,零偏壓電導峰最可能的來源就是Majorana零能模.

綜上,STM 實驗在 (Li,Fe)OHFeSe 磁通漩渦中觀測到清晰的零能模.它與其他低能磁通態明顯分離,沒有雜質效應的干擾.相比其他體系,這里觀察到的零能模顯示出“魯棒性”： 1)雖然局域超導能隙有不均勻性,但自由旋渦磁中心始終存在零偏壓峰； 2)由于相干長度較短,零能模能可在高磁場中存在,且磁通間耦合較弱； iii)較大的超導能隙和高Tc使該體系具有較強的抗熱擾動能力.因此,理論和實驗研究結果都表明重電子摻雜的(Li0.84Fe0.16)OHFeSe是拓撲非平庸超導體,為進一步研究Majorana零能模物性提供了一個理想平臺.

4 (Li,Fe)OHFeSe 磁通中 Majorana零能模的量子化電導

掃描隧道譜上的零能峰是Majorana零能模存在重要跡象,但還不是充分的證據.比如半導體納米線體系中的零能模就易和拓撲平庸的Andreev束縛態相混合[61,62].要證明零能峰就是Majorana零能模,還能夠反映其特征需要更進一步的實驗證據,其中之一就是電導的量子化.這是由于Majorana零能模具有粒子-空穴等價性,導致共振Andreev反射而產生的[41].該過程可類比于經典共振隧穿現象(圖6(a))： 即當電子隧穿通過一個量子點(或勢阱)時,如果兩端兩個電極與量子點間的隧穿勢壘相同,并且電子的能量與量子點內的某個束縛態能級一致時,就可以實現概率為1的完美隧穿,與勢壘高度無關.對于超導體,當一個電子入射到超導界面時會有一定概率反射回一個空穴,而在超導體內透射進入兩個電子形成Cooper對(Andreev反射).在STM實驗中,針尖既可充當電子發射極又是空穴的入射極(圖6(b)),這自然使得電子和空穴經歷的隧穿勢壘相等.而對于Majorana零能模,由于其“反粒子”為自身,粒子和空穴態完全等價.這使得電子通過Majorana零能模產生的Andreev反射完全滿足共振隧穿條件.Law等[41]通過理論計算嚴格表明,在零溫下Majorana零能模的電導將是量子化的2e2/h,與隧穿勢壘大小無關.而對于其他能隙內的束縛態,它們不滿足共振Andreev反射條件因而不具備該量子化電導.因此觀察到2e2/h的電導將是Majorana零能模存在的強力證據.

然而在實際測量中,零溫不可能達到,電導峰存在溫度展寬(= 3.5kBT),而且有限的超導能隙和其他準粒子態也會帶來額外展寬,因此觀察到量子化電導并非易事.理論模擬顯示[42],在有限溫度下只有當隧穿耦合強度遠大于溫度展寬時,才有可能探測到量子化電導(圖6(c)和圖6(d)).這意味著實驗中要盡可能地降低測量溫度并減小隧道勢壘.目前量子化Majorana電導在超導納米線體系的隧道結輸運實驗中有過報導[20].而對于磁通中的Majorana零能模,由于STM一般是工作在弱隧穿耦合(高隧道勢壘)的條件下,這就對實驗溫度和材料體系有了更高要求.但STM的優勢是局域測量,可將針尖精確地定位到磁通中心(即理論上只有零能模波函數分布的區域),這樣測到的電導易于排除其他態的干擾.前文介紹的是利用電子溫度Teff= 1.18 K的STM系統進行的測量.而本節將介紹在電子溫度Teff= 160 mK,能量分辨率為50 μV的稀釋制冷STM上對(Li,Fe)OHFeSe所做的測量,電導量子化平臺被成功觀察到.

圖7(a)給出了Teff= 160 mK 下(Li0.84Fe0.16)OHFeSe 磁通中心的隧道譜.相比于Teff= 1.18 K的結果(圖4),零能峰明顯變得更加尖銳.通過洛倫茲函數擬合這一零偏壓得到其半高寬為0.10 meV,這相比儀器能量分辨率0.05 meV只有輕微的展寬.圖7(b)給出穿過磁通中心的隧道譜,可以看出零偏壓電導峰的位置同樣不發生移動,與圖4(e)和圖4(f)中的結果一致.此外零能峰外側的其他磁通態也可以看到更多精細結構,值得進一步仔細研究,此處重點測量零偏壓峰.

圖6 共振 Andreev 反射與 Majorana 零能模的量子化電導 (a)經典共振隧穿[41]； (b) Majorana 零能模誘導的共振 Andreev 反射[41]；(c),(d)實際測量的Majorana零能模電導值與溫度和隧穿耦合強度的關系[42]Fig.6.Resonant Andreev reflection and quantized conductance of Majorana zero mode： (a) Conventional resonant tunneling；(b) Majorana zero mode induced resonant Andreev reflection (MIRAR)； (c),(d) the relationship between Majorana zero mode conductance and temperature,tunneling coupling strength.

圖7 (a)磁通中心處的微分電導譜,相應的隧穿電導是校正過的絕對值.藍色虛線： 利用洛倫茲函數來擬合零偏壓峰,相應的半高寬是0.10 meV； (b)圖(a)中的微分電導譜的空間二維顏色示意圖； (c),(d) 自由磁通1和2中心處隧道譜隨GN的變化(其中GN 定義為 Iset/Vb,對于磁通 1 為 Vb = —1.7 mV,磁通 2 為 Vb = —0.9 mV)； (e)—(f)對于磁通 2,不同 GN 下的四條典型的微分電導譜Fig.7.(a) Red curve： dI/dV spectrum at the core center.The tunneling conductance is calibrated by scaling to the numerical differential of the I/V curve.Blue dashed curve： Lorentzian fit to the ZBCP,with a FWHM = 0.10 meV； (b) spatial dependence of the dI/dV spectra in panel (a),shown in a false-color plot； (c),(d) evolution of the dI/dV spectra as a function of increased tunneling transmission for free vortex 1&2 reflected by GN = Iset/Vb (Vb = —1.7 mV for vortex 1 and Vb = —0.9 mV for vortex 2)； (e)—(f) selected dI/dV spectra taken at different GN for vortex 2.

圖8 (a),(b) 磁通 1 和 2 中心處隧道譜的零偏壓電導隨 GN 的變化 (GN 為 Iset/Vb)Fig.8.Summary of the zero-bias conductance as a function of GN for (a) Vortex 1,and (b) Vortex 2 (GN = Iset/Vb).

需要指出的是,要測量零能峰的量子化電導,標定STM隧道譜中的微分電導絕對值是非常重要的(這在通常的STM測量中常常被忽略).一般鎖相放大器的一階輸出雖然正比于微分電導,但絕對值會受各種硬件參數影響而不易計算準確.事實上微分電導可由I-V曲線直接數值微分得到,只是信噪比較低,但可用來標定鎖相放大器所測微分電導絕對值.此外,當隧道勢壘足夠小而隧穿又能保持穩定時,I-V曲線數值微分也能得到較好的信噪比,可以直接使用.還有一點是STM系統的隧穿回路引線一般有較大的電阻,通常是數百歐姆的量級.因為它們和隧道結串聯,在低隧穿勢壘的測量中會引入不可忽略的誤差.因此文獻[47]中通過將STM針尖直接接觸樣品測量了該電阻,排除了它對隧穿回路總電阻的貢獻.同時也排除了其他電子學器件帶來的誤差,比如為提高偏壓輸出精度所用的電阻分壓器的內阻.

雖然圖7(a)中零偏壓峰十分尖銳,但它是在高隧道勢壘下測量的 (隧道電阻為RN= 5 × 107Ω),其電導絕對值仍遠低于量子化的值G0(2e2/h=7.7 × 10—5Ω—1).為了增加隧穿耦合,實驗上需要逐漸減小針尖和樣品之間的距離.這一過程是通過固定設定偏壓值Vb,逐漸增大設定電流Iset來實現的.這里定義起始電導參數GN=Iset/Vb來反映隧穿耦合強度.圖7(c)和圖(d)為給出了兩個(無釘扎)磁通中心的隧道譜隨GN的變化.對于磁通1,隨著GN逐漸增大,零偏壓峰的電導迅速增大,同時峰也變得更寬,這來源于強隧穿耦合產生的展寬.但零偏壓電導到達約0.9G0后,進一步增加GN使得隧穿失穩.對磁通2,實驗成功觀察到零偏壓電導達到了量子化值G0.有意思的是,當起始電導GN足夠大時,非零偏壓峰的電導開始超過G0,但是零偏壓處電導可在一定范圍內維持在G0附近不變,此時的譜型反而變成零偏壓處產生“凹陷”(圖7(g)和圖7(h)).這一顯著特征反映出是Majorana零能模導致的零偏壓峰的電導量子化.

圖8中總結了兩個磁通中零偏壓電導隨著起始電導的變化關系.對磁通1,零偏壓電導在接近G0時開始出現飽和跡象.而磁通2則正好在G0處出現了一段量子化平臺! 該平臺位于GN= 0.75G0到GN= 1.0G0之間,說明在Teff= 160 mK等效溫度下,觀察到該體系共振Andreev隧穿的條件為GN＞ 0.75G0.而GN＞ 1.0G0時,實驗也觀察到零偏壓電導會繼續上升超過G0,這可能是來自附近非零能磁通態的貢獻,因為理論上強隧穿耦合時所有磁通態的峰的展寬都會變大,它們會相互疊加導致零偏壓電導的增大.

上述結果表明,STM在(Li0.84Fe0.16)OHFeSe樣品的非釘扎磁通中心觀測到的零偏壓峰擁有量子化電導的特性[47],這也進一步證明了它的起源是來自于Majorana零能模.類似的Majorana量子化電導近期在Fe(Te,Se)體系的磁通中心也被觀測到[63].這些結果有利于進一步理解Majorana零能模的物理特性.

5 單層 FeSe/SrTiO3 薄膜的磁通束縛態

如前文所述,(Li,Fe)OHFeSe 和 Fe(Se,Te)等體系中Majorana零能模的發現意味著鐵基高溫超導體中也可存在拓撲超導電性.第一原理計算也支持這些體系費米面附近存在拓撲非平庸的能帶結構,具有拓撲表面態.但鐵基超導家族十分龐大,不同體系能帶結構有很大不同,對比研究不同鐵基超導的磁通態會對它們的性質和來源有更深的理解.為此Chen等[47]進一步研究了SrTiO3襯底上生長的單層FeSe薄膜的磁通態.

單層FeSe/SrTiO3薄膜[64]也屬于重電子摻雜 FeSe 基超導體,但它和 (Li,Fe)OHFeSe還是有著明顯差別.首先單層FeSe是一個非常二維的體系,不存在體材料才有的層間耦合.以往的能帶計算也顯示其費米面附近沒有拓撲能帶反轉[28],只存在布里淵區M點處的電子型能帶[65,66].因此對比其磁通態與(Li,Fe)OHFeSe的差別將非常具有啟發意義.

此外,單層FeSe/SrTiO3的特殊之處還在于它具有鐵基超導體中最高的Tc(＞ 65 K)[64-66],比體相FeSe增加了近一個量級,因此其超導增強機理也成為關注的焦點.目前源于SrTiO3界面的電聲耦合[67]被認為是最有可能的超導增強因素.而要確定超導機理,一個重要方面是要確定超導配對對稱性.2015年Fan等[68]曾利用雜質效應和準粒子散射實驗表明單層FeSe/SrTiO3具有簡單s波配對.而最近有理論研究指出,如果該體系中存在一定強度的自旋軌道耦合,引起M點電子口袋的雜化,那么無節點的d波配對(nodeless-d wave)也有可能產生[69].這隨后也得到一些STM實驗的支持[70,71],因此該體系的配對對稱性仍然存在爭議.但需要指出的是,以往檢驗單層FeSe配對的實驗都是利用雜質相關的效應(比如表面吸附原子和表面原子臺階),這依賴于雜質的細節如散射勢強度[72]、雜質是否有磁性[73]等,但這些參數往往難以通過實驗來直接確定.理論表明磁通態的行為也和配對對稱性密切相關[1-3,74],而磁通態是磁場在材料內部產生的準粒子束縛態,不依賴于雜質,因而可能提供更本征的超導配對信息.這也是本節所要介紹的內容.

5.1 單層FeSe/SrTiO3薄膜的生長與磁通態測量

實驗測量的單層FeSe薄膜是利用超高真空分子束外延生長在Nb摻雜的SrTiO3(001)襯底上,生長完后通過退火處理以改善結晶度,相應的STM形貌見圖9.

圖9給出了樣品的典型超導能隙譜,為U型的雙相干峰結構,這與之前的多個研究一致[64,68].理解這種能隙結構的來源對于分析磁通態很重要.目前已知單層FeSe/SrTiO3的折疊布里淵區M點有兩個電子型口袋,且它們之間可能存在一定的雜化(無節點d波配對正是建立在這種能帶雜化的基礎上[69]).ARPES實驗已經觀測到單個電子口袋上明顯的能隙各向異性,但是在實驗分辨率范圍內還沒有觀察到能帶的雜化[75,76].為了理解雙相干峰的產生,這里采用了文獻[76]中ARPES實驗得到一個單帶能隙各向異性函數公式：

如圖9(d)所示,這一能隙函數會產生兩個局部能隙的極大值Δ2=Δ0+A+B,以及Δ1=Δ0-A+B.這兩個局部能隙的極大值在STM的dI/dV譜上會產生兩對超導相干峰,而費米面上的平均能隙大小為Δ0.圖9(b)中的紅色曲線即能隙的擬合結果,擬合系數Δ0= 10.58 meV,A= 3.25 meV,B= 2.87 meV.

施加垂直磁場后,零偏壓電導成像可觀測到單層FeSe區域中形成的磁通渦旋,見圖9(c).其中部分磁通被表面的不規則雜質所釘扎(圖中的綠色箭頭所示).在多數情況下,表面雜質附近可以觀察到能隙束縛態[48].為了避免這些雜質態的影響,實驗上僅研究非釘扎磁通,它們所在的區域在零場下表現為干凈的超導能隙.圖9(e)和圖9(f)給出了這些磁通上的測量結果示例.其磁通中心也觀測到多個清晰分立的束縛態,但不存在零偏壓電導峰.總體而言,這些非零能磁通態相對于費米面對稱分布且間距相等,峰位在磁通中心一定范圍內保持不變.遠離磁通中心時這些低能分立的峰逐漸消失,同時在較高能量下出現一對較寬的峰(圖中的藍色陰影區域).隨著遠離磁通中心,那些較寬的峰將繼續向高能量移動,并最終合并入超導相干峰.

圖9 (a) SrTiO3 襯底上生長的 FeSe 薄膜形貌 (平均厚度 1.3 層)； (b)單層 FeSe 薄膜的典型超導能隙譜 (Vb = 30 mV,I = 60 pA,T = 4.2 K),藍色點為 B = 0 T 磁場下的實驗數據,紅色曲線是擬合的結果； (c) B = 10 T 時的零偏壓微分電導成像,綠色箭頭所指的是雜質釘扎的磁通,虛線圓圈里是未釘扎的自由磁通； (d) 布里淵區M點費米面上的能隙分布示意圖.Δ2,Δ1和Δmin分別對應于兩個局部能隙最大值以及一個能隙最小值,并且tg(θk)=ky/kx； (e),(f) 穿越磁通1和3中心的路徑上0.4 K溫度下所測量的微分電導譜(等效電子溫度Telec = 1.18 K),顯示出清晰分立的磁通態(無零偏壓峰)Fig.9.(a) STM image of FeSe/SrTiO3 film with a thickness of ～1.3 ML； (b) typical gap spectrum (blue curve) of 1 ML FeSe (Vb =30 mV,I = 60 pA,T = 4.2 K) taken at B = 0 T and the fitted gap is shown in red curve； (c) zero-bias dI/dV mapping taken at B =10 T.Green arrows indicate surface defects and the pinned vortices,dashed circles indicate free vortices； (d) sketch of the gap distribution on the electron pocket at M.Δ2,Δ1 and Δmin correspond to the two local gap maxima and the gap minima,respectively,and tg(θk) = ky/kx； (e),(f) dI/dV spectra taken across Vortex 1 and 3 at T = 0.4 K (Telec = 1.18 K).Discrete vortex states (without zero bias peak) were observed.

圖10給出了四個磁通束縛態分布的定量分析,通過精確的峰位擬合,發現這些磁通態峰位與平均間隔δE的比值很好地位于半整數值(±1/2,±3/2或±5/2)的線上(圖10(e)),這符合常規s波超導體CdGM磁通態的理論預期[1,24].遠離磁通中心時較高能量處的峰其實是一系列高階磁通態疊加的效果,它們在遠離磁通中心的過程中也不斷往更高能量處移動,這也與一般超導體磁通態的行為一致(如NbSe2[22,23]).

對于不同的磁通,其束縛態的能量間隔δE存在一定差異,這是由每個磁通附近局域的超導能隙不完全相同所致.圖10(g)給出了四個磁通附近測量的超導能隙譜和經過擬合得到的平均能隙大小(Δ0).而利用 (Δ0)2/EF可以合理地解釋不同磁通處觀測到的不同的能量間隔δE(圖10(f)).所以單個各向異性的超導能隙可以同時解釋超導雙能隙結構和分立的磁通束縛態,而無需考慮能帶雜化.

5.2 不同配對對稱性下磁通態的理論模擬

以上分析顯示單層FeSe/SrTiO3磁通態行為與s波超導體類似,但該體系還有其他配對對稱性的可能,因此有必要檢驗其他配對下磁通態的行為.為此文獻[48]分別針對s波和無節點d波配對[69]兩種情形計算了單層FeSe磁通中心的束縛態分布.該模擬計算基于兩帶k·p模型來描述低能超導準粒子[69],其動量空間中的哈密頓量表達式是：hk=?k+dkσ3+gk·sσ1.這里σ1,2,3是作用在軌道上的泡利矩陣,s1,2,3是作用在自旋上的泡利矩陣.將這一模型應用到晶格上,有：

其中系數t′表征橢圓費米口袋的各向異性,λ是自旋軌道耦合強度.根據實驗這里設定t≈ 135 meV,μ= —3.63t(或EF= 0.37t),t′= 0.125t來模擬單層 FeSe/SrTiO3的實際能帶.另外基于最近的ARPES實驗[76],將自旋軌道耦合強度上限設定為5 meV.

圖10 磁通束縛態的定量擬合 (a)—(d)自由磁通1—4中心的低能量的微分電導譜.其中紅色的曲線是多個高斯峰擬合的結果(虛線是單個高斯峰)； (e)通過除以磁通1—4中的束縛態的平均能量間隔δE得到的每個磁通中心的CdGM束縛態的歸一化能量； (f)對于自由磁通1—4,(Δ 0)2/EF 與能量間隔 δE的關系,虛線是線性的擬合曲線； (g)是自由磁通1—4出現位置處的不加磁場時超導能隙,平均超導能隙的大小Δ0是通過函數擬合得到Fig.10.Quantitative fitting of vortex bound states： (a)—(d) Low energy spectra of free Vortices 1—4.Red curves are multiple Gaussian-peak fits (Dashed curves are individual peaks)； (e) normalized energy of the CdGM state of Vortices 1—4,via dividing the averaged δE of each vortex； (f) the relation of (Δ 0)2/EF and δE for Vortices 1—4,dashed line is the linear fitting.(g) superconducting gap spectra taken at the area where Vortex 1—4 appear (B = 0 T).The mean gap sizes (Δ0) are obtained from the gap fitting.

對于s波對稱性,哈密頓量里的配對部分寫為Δk=Δ0σ0is2.令Δ0= 0.07t(約 10 meV),計算得到的磁通態密度如圖11(b)所示.可以看到磁通態以相等的間距對稱分布在費米能量兩側,即是典型的CdGM磁通束縛態.隨著靠近磁通中心,低能態的強度增加并表現出一定的粒子-空穴不對稱性[24],定性上與實驗結果一致.在考慮一定強度的自旋軌道耦合后,計算得到的CdGM束縛態沒有明顯變化(圖11(c)).這是因為對于s波配對情形,盡管自旋軌道耦合誘導了能帶雜化,但它僅使兩個雜化能帶的化學勢稍微向相反方向移動(EF′=EF±λ),而超導能隙的大小保持不變.當自旋軌道耦合的強度λ?EF時,CdGM磁通束縛態的能量E=μΔ2/(EF±λ)的變化太小在實驗上無法探測.

圖11 理論計算的 s 波和無節點 d 波的磁通束縛態 (a),(d) s 波和無節點 d 波配對的費米面示意圖； (b),(e) 分別是在距離磁通中心不同距離處沒有自旋軌道耦合的s波配對、自旋軌道耦合強度λ = 0.02t下的無節點d波配對的磁通態情形(ξ是相干長度,λ是自旋軌道耦合強度)； (c),(f)分別是距離磁通中心固定距離d = 0.1ξ的不同自旋軌道耦合強度下的情形 (c)是不同自旋軌道耦合強度λ的s波配對,(f)是無節點d波配對Fig.11.Calculated vortex states under s-wave and nodeless d-wave pairing.Sketch of the Fermi surface for (a) s-wave (d) nodeless d-wave pairing.(b),(e) Calculated vortex states at different distance to the core center for (b) s-wave (e) nodeless d-wave with λ =0.02t (ξ is the coherence length and λ is SOC strength).(c),(f) Calculated vortex states under s-wave (c) and nodeless d-wave(f) pairing at d = 0.1 ξ,with various SOC strength.

對于無節點d波配對,則必須存在有限的自旋軌道耦合來避免能帶的交叉.在這種情況下兩個口袋上都有完全的能隙,但符號發生變號(如圖11(d)).計算表明此時存在來自兩個雜化帶的兩組CdGM束縛態(圖11(e)),并且這兩套峰在能量上從費米能量開始向著相反的方向移向.更進一步,這種能量的移動大小具有和自旋軌道耦合強度λ相當的量級(圖11(f)).這從現象上可以理解為： 對于無節點的d波,自旋軌道耦合項直接進入BdG方程,并且決定了準粒子的色散.因此,自旋軌道耦合在這里影響著BdG準粒子的“化學勢”偏移,然后導致磁通態的能量峰位發生移動,即E=(μΔ2/EF)±λ(其中“+”和“—”符號分別對應于兩個不同的能帶).

但無節點的d波配對的計算結果與STM的實驗數據相矛盾.在STM測量過程中,盡管局域的超導能隙和磁通態的能量間隔δE在不同的磁通位置存在一定差異,但在實驗誤差范圍內(≤ 0.02 meV),這些磁通態在能量上關于費米能量對稱分布,且等能量間隔,從未觀察到兩套能量發生移動的CdGM態.事實上,任何不對稱的能量偏移或劈裂大于儀器分辨率(0.36 meV)的情況下,都可以在掃描隧道譜上被觀測到.由于自旋軌道耦合對于這種無節點d波配對模型來說是必需的條件,并且根據文獻[69]所述,解釋角分辨光電子能譜實驗觀察到的能隙各向異性需要一定大小的自旋軌道耦合強度,因此STM對于磁通束縛態的實驗結果不支持這種無節點的d波配對模型.

另外對于d波配對超導體,理論上在{[110]}取向的疇界處將存在零能Andreev束縛態[77](因為準粒子反射中存在π相移).而常規s波超導體的邊界處通常不會產生能隙束縛態.文獻[48]也報導了對[110]Fe方向邊界上的測量,包括單原子臺階邊緣和雙層FeSe與單層FeSe之間的疇界.總體而言,在這兩種不同類型的[110]取向的邊界上均沒有觀察到零能Andreev束縛態,與d波或拓撲超導體的預期不符,但與普通s波配對理論相一致.所以上述磁通CdGM束縛態和邊緣態兩方面研究為單層FeSe/SrTiO3薄膜配對機制提供了獨立的實驗線索,有助于澄清最近關于其配對對稱性的爭議.

總之,上述實驗結果為鐵基體系中的拓撲超導研究提供了重要參考.層間耦合作用在Fe(Se,Te)和(Li,Fe)OHFeSe材料中會產生能帶反轉和拓撲表面態,最終導致磁通中的Majorana零能模.對于二維的單層FeSe薄膜系統,盡管最近的研究表明該體系中在費米能量以下的M點處存在由自旋軌道耦合誘導產生的能隙[78],但是STM實驗在磁通中心沒有觀測到零偏壓峰,且一維邊界上不存在能隙內的Andreev束縛態,表明單層FeSe是拓撲平庸的體系.因此,這一實驗結果也進一步表明了層間耦合是鐵基體系中實現拓撲超導的重要先決條件.

6 總結與展望

尋找適用于實現拓撲量子計算的Majorana零能模是當今凝聚態物理最熱門的研究話題之一,其中一個重要方向就是在拓撲超導體磁通中心探測Majorana零能模.本綜述重點介紹了利用極低溫STM對鐵硒類高溫超導體(Li,Fe)OHFeSe和單層FeSe/SrTiO3薄膜的研究.在 (Li0.84Fe0.16)OHFeSe超導體的自由磁通中心觀測到清晰的Majorana零能模和量子化電導,而單層FeSe/SrTiO3薄膜的磁通中只發現常規非零的CdGM磁通態.這系列研究為進一步探索Majorana零能模提供了優越平臺,也為理清鐵基超導中Majorana零能模的來源提供重要線索.

迄今,Majorana零能模已在多種體相鐵基超導中被發現,比如 Fe(Se,Te)[33-35],(Li,Fe)OHFe Se[46,47],CaKFe4As4[79]等,在其他 材料如 WS2[80]中也有報導.雖然Majorana零能模已經在相關的體系中被成功觀測到,但是很多相關的物理特性還有待進一步的實驗測量,如空間分布特征[24,44]、自旋極化特征[44,45]、非阿貝爾統計特性[9,10]等.這些物理性質的實驗觀測有助于對Majorana零能模有一個更加全面、深入的認識,以便后續進一步探索Majorana零能模的編織操作、構建以此為基礎的拓撲量子比特等.

另外,近期理論和實驗在探索實現Majorana零能模的新途徑上也有重要進展.最近的一項理論工作指出： 超導體表面的單個磁性原子在一定條件下能引起自發的磁通,等效于外加磁場形成的磁通渦旋.因此單個磁性原子也可能誘導出Majorana零能模[81].實驗上也曾在Fe(Te,Se)體系的Fe原子上觀測到零偏壓峰[82].這些結果為操縱編織Majorana零能模提供了另一種方案.

“路漫漫其修遠兮”,作為實現拓撲量子計算的重要載體,Majorana零能模的研究在近幾年不斷有新的理論和實驗的突破,相信該領域在未來也將會有更旺盛的生機和活力.

感謝合作者董曉莉、趙忠賢提供(Li,Fe)OHFeSe樣品,并感謝本文所述工作所有其他合作者： 殷志平、王強華、鮑偉成、彭瑞、閆亞軍、文陳昊平、樓廈、張天真、黃裕龍、王廣偉、田金朋、李棟、沈沛沛； 感謝張富春、胡江平、王靖、Dunghai Lee、Chun-Xiao Liu、Darren Peets、王熠華給予的有益指導和建議.