一種適應大數據處理要求的深層學習模型

徐承俊 朱國賓

(武漢大學遙感信息工程學院 湖北 武漢 430079)

0 引 言

大數據在帶來豐富信息和寶貴資源的同時，也給處理數據、分析數據等工作帶來了巨大的壓力和嚴峻的挑戰。如何高效開發和利用大數據，挖掘其背后隱藏的有價值的信息，利用大數據更好地把握和預測未來各領域發展趨勢，更好地為人類服務，是數據挖掘和機器學習領域的核心問題之一。深度學習是目前應用最廣泛的學習方法和框架之一，其模型框架使用監督/非監督學習，已成功應用于新型數據驅動態勢感知[1]、基于大數據醫療保健治療[2]、信息服務[3]和工業大數據應用[4]等領域。小米、阿里巴巴和新浪等IT巨頭都已經加大對大數據的投入、采集、分析和研發，推出各種個性化服務，如：阿里基于大數據深度學習框架為用戶推薦爆款商品、道路路況擁堵、新聞推送等[5]；百度也推出了地圖匹配和搜索、聯想輸入等；微軟的語音同步翻譯與IBM人工智能也都使用了深度學習框架[6]。雖然深度學習在上述領域已表現出巨大優勢，也取得了很好進展，但仍舊存在不足，主要表現為以下幾個方面：

(1) 數據信息缺失等不完整性。大數據中含噪聲數據，如屬性、參數缺失等。目前模型針對標準數據集，而面對實時數據時稍顯不足。

(2) 大數據的海量性。模型訓練中數據量大、類型多，數據結構復雜度高，普遍采用云存儲、云計算，但會導致數據安全等問題。

(3) 數據的動態性。目前使用的深度學習框架基本是靜態模型，執行過程中不能更改，故無法滿足實時動態變化需求。

(4) 數據的異構性。大部分現有模型基于向量空間表示，適用于處理一維或者二維數據，很難處理高維異構數據，存在局限性。

為了有效克服上述問題，本文分析大數據特征并針對上述問題中的動態性和異構性提出以下解決方法：(1) 設計遞增式迭代深層學習模型，主要針對數據結構和參數進行更新，提高模型對新進數據的拓展適應性，滿足大數據變化要求；(2) 數據結構采用張量表示，將數據表示從一維、二維向量空間擴展到高維張量空間，構建更深層次模型。

1 遞增式迭代深層學習模型

大數據變化快、數據量大，需要及時進行處理，以獲取最新信息。所以要求算法、模型能適應此要求。遞增式迭代深層學習模型即在原模型基礎上，保留原訓練參數忽略原結果，只對新進數據更新模型參數或結構，學習新特征，即在保存原模型參數、知識結構的同時具備學習新特征的能力。

機器學習中傳統模型訓練是將整個訓練集同時送入模型進行訓練，此過程中無法對模型參數或結構進行動態更新，無法滿足實時性要求，存在局限性。

為了克服上述問題，本節提出一種支持大數據實時更新的深層計算模型，主要是對模型參數或結構更新。在參數更新方法中，借鑒一階微分思想，不采用傳統迭代的方式進行求解，避免了原數據集的再次訓練，從而提升參數更新速度，使得新模型能快速學習新數據特征。訓練時若增加模型節點，則將獲取的新參數與原參數有機結合后賦值于新模型的新初始值，這樣在原有模型參數基礎上，加快計算速度，使其更快收斂。

1.1 問題概述

實現支持遞增迭代式更新的深層計算模型需要將多個此計算模型進行合理疊加，組建支持遞增更新的更深層次計算模型。在接收新進數據后，其目標是保存原模型參數，不再重新訓練原數據集，引入新進數據時更新模型的參數與結構，學習新數據特征，即此模型既要完成保留原模型參數，又要實現對新數據進行訓練學習。該模型需要滿足下面三個原則：

(1) 拓展適應原則。改進的新模型具有對新進數據集特征學習的能力，能適應大數據實時變化。

(2) 兼顧原則。新模型既保留原模型參數，又訓練新數據參數等。

(3) 遞增原則。在接收新數據時，保留原數據特征參數等信息，不再訓練原始數據集，僅訓練新進數據。

實現上述功能有多種方式和方法，本節主要討論以下兩種方式：

(1) 結構更新。大數據更新快、數據量大，主要通過增加隱藏層神經元數目對模型結構、參數進行更新。傳統機器學習中，數據結構表示是向量，可以直接增加若干個隱藏層神經元，但是遞增式迭代深度學習模型處理的數據結構是張量，要根據其結構和類型確定增加的神經元數目。

(2) 參數更新。當新進數據特征變化不明顯，可以通過對原模型參數更新，實現模型更新。

1.2 結構更新的遞增式迭代深層學習模型

結構更新即增加隱藏層神經元數目實現對原模型修改。一個具有m個輸入變量和n個隱藏層神經元的自動編碼機，其原始模型結構如圖1所示，其中“+1”表示新增加的1個神經元。

圖1 原始模型結構

設模型參數η={k(1),t(1),k(2),t(2)}，表示如下:

k(1)∈Rm×nt(1)∈Rmk(2)∈Rm×nt(2)∈Rn

(1)

增加1個隱藏神經元后的新結構如圖2所示，調整參數，以適應新進數據學習。權重k(1)、k(2)分別增加1行1列，k(1)∈R(m+1)×n,k(2)∈Rm×(n+1),t也增加1個分量t(1)∈Rm+1。

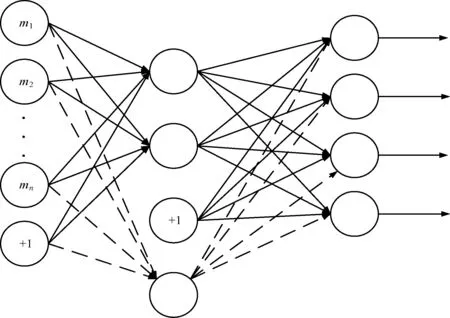
圖2 改進后的模型結構

增加隱藏層神經元并賦值新增參數為0。當前參數η={k(1),t(1),k(2),t(2)}，增加p個隱藏神經元后的初始參數表示如下：

(2)

新模型參數η={k(1)′,t(1)′,k(2)′,t(2)′}，使用反向傳播方法求模型的最終參數。然后考慮將模型擴展到高維空間，設計基于增加隱藏層神經元的模型結構更新算法。一般只需增加若干個神經元，而對于高維模型，則需要考慮高維模型的結構特征。

如果一個輸入變量為g∈RS1×S2，隱藏層l∈RU1×U2，設η′={k(1),t(1),k(2),t(2)}，表示為：

k(1)∈Rυ×m×n(υ=U1×U2)t(1)∈RU1×U2k(2)∈R?×m×n(?=S1×S2)t(2)∈RS1×S2

(3)

式中：υ、?表示神經元作用域范圍。

若隱藏層增加U1個神經元后其結構為l′∈RU1×(U2+1)，對應的參數為η′={k(1)′,t(1)′,k(2)′,t(2)′}，表示為：

k(1)′∈Rυ′×S1×S2(υ′=U1×(U2+1))t(1)′∈RU1×(U2+1)k(2)′∈R?′×U1×(U2+1)(?=S1×S2)t(2)′∈RS1×S2

(4)

式中：υ′表示新增U1個神經元作用域范圍。

增加U2個神經元后的隱藏層結構l′∈R(U1+1)×U2，其參數為η″={k(1)″,t(1)″,k(2)″,t(2)″}，表示為：

k(1)″∈Rυ″×S1×S2(υ″=(U1+1)×U2)t(1)″∈R(U1+1)×U2k(2)″∈R?′×(U1+1)×U2(?=S1×S2)t(2)″∈RS1×S2

(5)

式中：υ″表示新增U2個神經元作用域范圍。

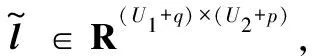
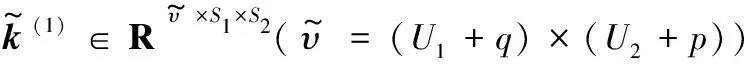
(6)

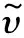
輸入變量g∈RS1×S2×…×SN模型一般形式，隱藏層結構l′∈RU1×U2×…×UN，參數η={k(1),t(1),k(2),t(2)}表示為：

k(1)∈Rχ×S1×S2×…×SNχ=U1×U2×…×UNt(1)∈RU1×U2×…×UNk(2)∈Rδ×U1×U2×…×UNδ=S1×S2×…×SNt(1)∈RS1×S2×…×SN

(7)

(U2+p2)×…×(UN+pN)

?=S1×S2×…×SN

(8)

結構更新得到新模型后，將新模型中參數的新增分量初始值賦為0，應用算法1計算新模型最終的參數。

算法1反向傳播算法

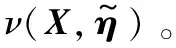
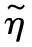
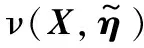
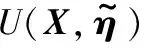
Step5采用梯度下降算法取合適步長進一步更新模型參數，找出最優解。

Step6重復Step2-Step5直到模型收斂。

根據原模型訓練結果得到參數，加上新進數據參數不斷調整，并與原模型參數有機結合作為新模型初始參數值，因此新模型在原有參數基礎上訓練，其收斂速度更快，更好地滿足數據變化需求。

1.3 模型實施

支持遞增更新的深層學習模型有兩個階段：預先訓練與局部微調。第一階段，通過參數或結構更新采用自下而上遞增迭代的方式完成各分支模塊的訓練，將訓練后的多個遞增式模型疊加，組成更深層次模型。第二階段，使用有標簽數據對參數進行調整訓練，通過前向傳播和反向傳播算法相結合使用，計算獲得最后參數。

1.4 參數更新的深層學習模型

參數更新方法不同于1.2節中的結構更新，不需要對模型結構調整與修改，只需要根據新進數據特征將原參數η更新為η+Δη，使其能夠適應學習新數據特征，參數更新的模型參數η={k(1),t(1),k(2),t(2)}，數據結構由低維向量擴展成高維張量組成。t(a)(a=1,2)與k(a)(a=1,2)由N維、N+1維張量表示，借鑒一階近似導數思路，在不改變結構的基礎上調整參數來滿足數據處理實時性要求。

(9)

Δanew=ν(a,η+Δη)-a表示計算模型從η更新到η+Δη的新誤差。其中：η為原參數，η+Δη為新參數，ρ表示學習效率，a為與I同階的一個參數。

同理，定義保持性誤差函數：

(10)

式中：γ表示誤差因子，在本文中取值為0.3。

兼顧保持性與拓展適應性，其代價函數U(a,η+Δη)表示為：

U(a,η+Δη)=Uadaption+Upreservation

(11)

參數更新模型的方法是找尋使得式(11)最小值來求解遞增Δη，對其進行泰勒公式應用展開求解：

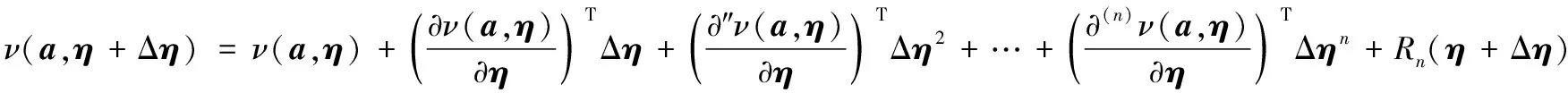
得到代價表示函數U(a,η+Δη)近似為：

根據求導法則，令導數等于0后并對Δη求導，得近似值，如下：

進一步繼續求解，得到：

(12)

式中：Δη和η表示參數張量的變化量和張量，類似線性梯度下降算法；Δa表示模型輸出值與a的差值。

算法2參數更新算法

Step1根據前向傳播方法計算遞增式迭代深度學習模型輸出值ν(a,η)。

Step2求解遞增式迭代深層學習模型的輸出與x的差值Δη。

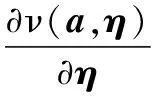
Step4應用式(12)計算新模型參數的Δη遞增值，將模型參數更新為η+Δη。

根據算法2，當新進數據進入模型并完成加載后，模型可完成對其訓練、學習，完成參數更新等操作，且無須對原始數據重復訓練，只對新進數據訓練，具有很高的拓展適應性，能提高計算性能。

2 基于張量表示的深度計算模型

不同于傳統數據，大數據包含大量非結構化、半結構化和結構化數據。傳統機器學習模型和算法是基于結構化數據，而大數據中通常包含視頻、語音和圖像等半結構化、非結構化數據，約占總數據的80%以上[7]。

當前模型主要是對單一數據結構的特征學習，2010年Ngiam等提出多模深度學習模型，能夠學習語音與圖像特征。2012年Srivastava等提出多模深度玻爾茲曼機，能夠學習文本與圖像特征。雖然上述模型能解決部分問題，但依舊存在模型學習效率低等問題。根本原因是其數據結構是采用向量表示，表達高維數據時信息易丟失。

本文針對上述問題，提出一種應用張量對異構數據進行表示的方法。將向量表示擴展到張量表示，構建基于張量空間模型，并且使用張量距離替代歐氏距離構造誤差函數，減少誤差和損失。設計基于張量的高階反向傳播算法求解參數，然后將多個高階模型進行疊加，構建更深層次模型。主要思路如下：

(1) 異構數據采用張量的表示方法，使該模型能夠學習各類異構數據，并將高維模型進行疊加，組成更深層次模型，實現多層學習。

(2) 使用張量距離而不是傳統歐氏距離構建誤差函數。

(3) 設計基于張量的反向傳播算法。

因此，本文從以下幾個方面解決張量的深度學習模型的關鍵問題：

(1) 傳統模型是以向量、矩陣表達和計算的，如何使用張量來描述，使得數據更加準確是第一個關鍵問題。

(2) 傳統歐氏距離在張量表示的高維空間受理論知識限制，導致數據特征表示不準確，故采用張量距離表示誤差函數。

(3) 反向傳播算法大都基于向量表示空間設計的，無法用于張量表示，所以需要設計基于張量空間的反向傳播算法以適應新模型。

2.1 張量的數據表示

1890年沃爾德馬爾·福格特提出張量[8-10]，本文中使用的一些定義及運算[11-12]如下:

定義1張量：令G1,G2,…,GN是維數為H1,H2,…,HN的N個有限維的歐氏空間，設N個向量u1∈V1,u2∈V2,…,uN∈VN，定義V1×V2×…×VN的多線性映射u1°u2°…°uN為：

(u1°u2°…°uN)(a1,a2,…,aN)=

V12…VN

(13)

式中：Vi表示Vi上標量積，ai(i=1,2,…,N)為Gi上的任意向量。則全體(u1°u2°…°uN)構成G1,G2,…,GN的張量空間，該空間上元素稱為G1,G2,…,GN上的N階張量。特別地，如果Gi=ZIi(i=1,2,…,N)，則張量空間為N階H1,H2,…,HN維實張量空間，表示為RH1×H2×…×HN。

定義2張量的n階展開：令A∈RH1×H2×…×HN為一個N階張量，其n階展開為Hn×(H1H2…Hn-1Hn…HN)矩陣，用A(n)表示，第(in,j)個元素為Ai1 i2 …iN。

特別地，一個N階張量A∈RH1×H2×…×HN可以展開成一個向量a。

定義3張量的外積：對于一個N階張量A∈RH1×H2×…×HN和M階張量B∈RU1×U2×…×UM。外積產生一個(M+N)階張量C∈RH1×H2×…×HN×U1×U2×…×UM，其元素Ch1,h2,…,hN,u1,u2,…,uM被定義為：

Ci1,i2,…,iN,j1,j2,…,jM=si1,i2,…,iN·tj1,j2,…,jM

(14)

式中：s、t分別表示張量A、B中的元素。

定義4張量的多點積：對于兩個N階張量A,B∈RH1×H2×…×HN，A和B的多點積產生一個張量C，且：

(15)

一幅彩色圖像用一個3階張量表示，一個視頻文件用一個4階張量表示。例如，彩色圖像用ZSW×SH×SC,其中SC、SW、SH分別表示該圖像顏色通道、寬度和高度。一幅256×256像素的彩色圖像表示為Z256×256×3，通常轉換成灰度圖像：

G=0.299R+0.587G+0.114R

(16)

對于一個視頻文件ZSW×SH×SC×SA，SC、SW、SH分別表示圖像顏色通道、寬度和高度，SA表示視頻的維度。如一個15秒的MP4視頻文件，設每秒20幀，每一幀由一幅圖片組成，則該視頻表示為R256×256×3×300。

2.2 高維自動學習編碼機模型

定義5張量的多點乘積⊙：對于N+1階張量k∈Zυ×S1×S2×…×SN和N階張量g∈ZS1×S2×…×SN，其中k具有α個N階子張量，每個子張量k?∈ZS1×S2×…×SN。k和X的多點乘積得到N階張量l∈ZU1×U2×…×UN(U1×U2×…×UN=υ)，l=w⊙X。

與傳統模型不同，新模型每一層是一個張量，而不是一個向量，其他相同。設g∈ZS1×S2×…×SN，l∈ZU1×U2×…×UN表示輸出層和隱藏層變量。將輸入變量X經過fθ映射到隱藏層l：

l=fθ(k(1)⊙a+t(1))

(17)

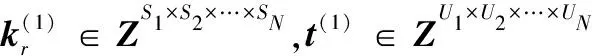
同時，解析函數gθ將隱藏層映射回重構函數Y:

Y=hk,t(a)=gθ(k(2)⊙l+t(2))

(18)

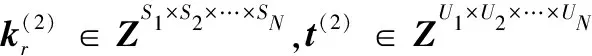
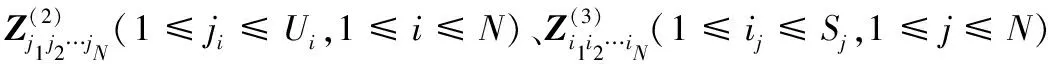
(19)

(20)

(21)

(22)

式中：w為權重；b為偏移量。

文獻[13]使用張量距離重構誤差函數，對于兩個張量X∈RI1×I2×…×IN、Y∈RI1×I2×…×IN，x和y分別表示張量X和Y按向量展開后形式，則張量距離表示為：

(23)

式中，glm是稀疏；G是矩陣的系數，反映高階數據不同坐標內在的聯系；xl、xm、yl、ym分別表示張量X和Y對應的元素。

(24)

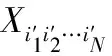
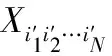
‖pl-pm‖2=

(25)

設訓練集{(X(1),Y(1)),(X(2),Y(2)),…,(X(m),Y(m))}中包含m個訓練集，對于任何一個實例(X,Y),將其展開對應向量(x,y)，其重構誤差函數:

(26)

式中:遞增式迭代深度學習模型參數θ={W(1),b(1),W(2),b(2)}，在自動學習編碼模型中令X=Y。對于整個訓練集，基于張量距離的遞增式迭代深度計算模型重構誤差函數為：

(27)

式中：第一項表示平均誤差；第二項是一個規范化項，主要是防止過度擬合。

2.3 高維反向傳播

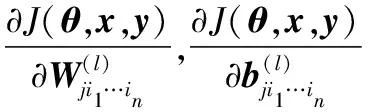
(1) 前向傳播計算，計算z(2)、z(3)、a(2)、a(3)；

(2) 對于輸出層每個神經元i，計算殘差:

(3) 對于隱藏層每個神經元，也計算殘差:

(4) 對于隱藏層和輸出層每個神經元，計算殘差:

(5) 當l=1,2時，計算偏導數:

2.4 深度學習模型

構造更深層次計算模型將多個高維模型疊加，其訓練主要有：預先訓練與局部微調。訓練過程可用于異構數據監督特征學習，如圖3所示。

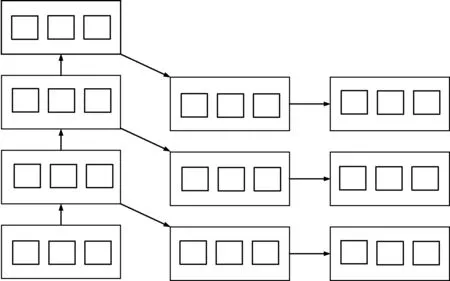
圖3 訓練模型圖

完成預訓練后，可以根據每個數據對象的類標簽，進行有監督學習，對模型進行局部參數微調，獲得最后模型參數，如圖4所示。向量是1階特殊張量，此模型可以作為深度學習模型的擴展。

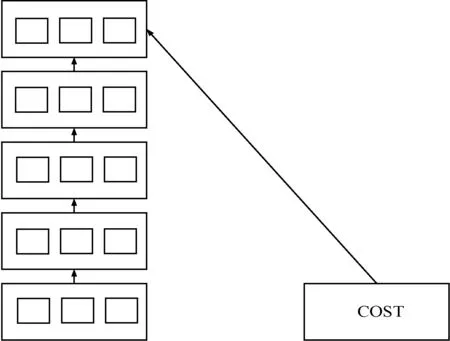
圖4 參數調整模型圖

3 實驗與分析

數據集選擇ImageNet中STL-10，其中包含500幅訓練圖像和800幅測試圖像，總共有10個分類[14]，并且包含100 000幅未被標記的圖像，可用來進行無監督訓練。

數據集中每幅圖像用一個3階張量表示，因為訓練集與測試集變化不大，參數的更新很小，所以只需通過參數更新就能實現模型對新數據特征學習。為進一步驗證本文提出的模型有效性，將STL-10數據集進行如下設計：

(1)T0：訓練數據集含500幅圖像；

(2)T1：測試數據集隨機抽取300幅圖像作為新增訓練集；

(3)T2：測試數據集中剩余圖像作為測試集。

根據以上數據集訓練如下參數：

(1)η(TAE)：根據T0運行基本的模型，得到模型參數η；

(2) ITAE-1：以上一步得到的η為初始參數，執行T1近似一階導，支持遞增更新深層模型，獲取更新參數ITAE-1；

(3) TAE-2：在T0+T1運行更新前模型，獲取參數TAE-2；

(4) TAE-3：在數據集T2運行更新前模型，獲得參數TAE-3。

實驗以T2為測試數據集，計算均方誤差(MSE)驗證以上參數對T2測試數據集分類的正確性。主要目標是驗證以上參數是否能對新數據有適應能力，MSE越小說明適應能力越強。實驗10次，結果如圖5所示。

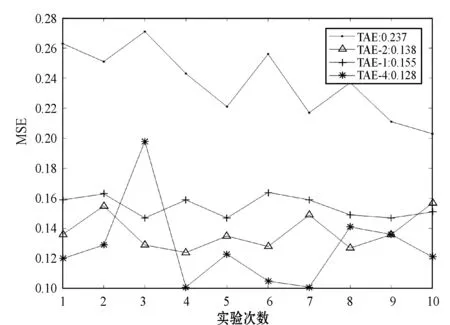
圖5 STL-10實驗結果

均方誤差(平均結果)統計如表1所示。

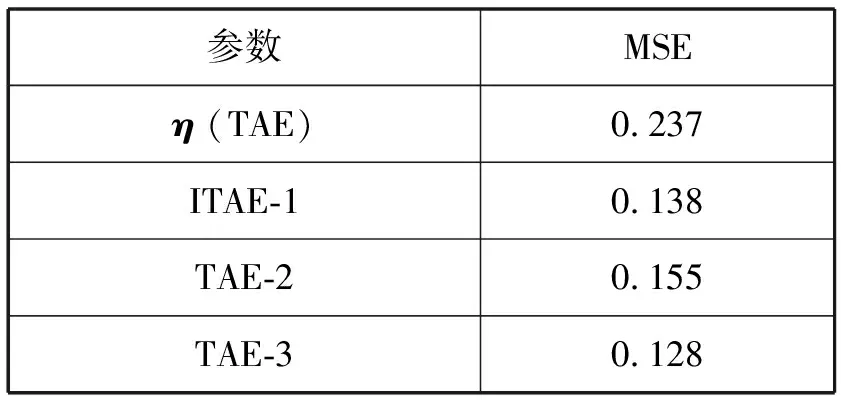
表1 MSE統計結果(適應性)

可以看出，以η為參數對T2進行分類，得到MSE的值最大，因為原始計算模型是靜態的，參數確定好之后，無法更新，很難學習到新的數據特征。而本文模型能實現對參數更新，進而對新數據進行學習。

以T0為測試數據集，計算MSE驗證以上參數對T0測試數據集分類的正確性。主要目標是驗證以上參數是否具有保持原數據的能力，MSE越小說明適應能力越強。實驗10次，結果如圖6所示。

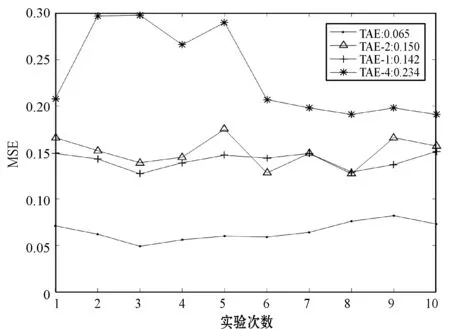
圖6 保持性實驗結果

均方誤差(平均結果)統計如表2所示。

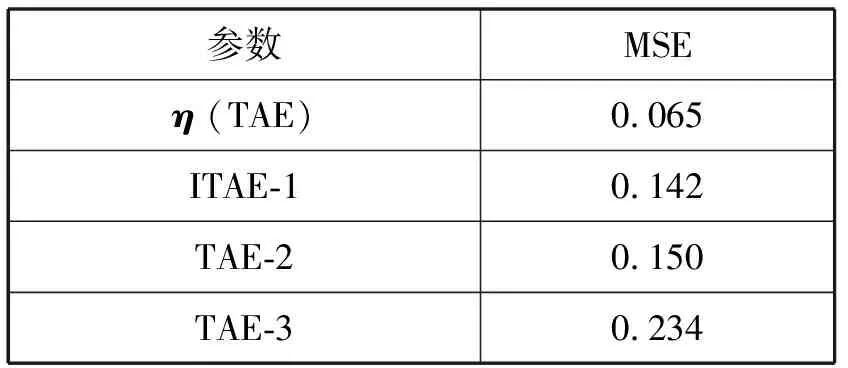
表2 MSE統計結果(保持性)

實驗結果表明，以η為參數對T0進行分類得到MSE最小，因為η是基于T0進行學習獲得的參數。以ITAE-1和ITAE-2為參數T0進行分類，得到MSE結果依然很低，說明兩種算法對歷史數據具有較好的保持性，而ITAE-3獲得的MSE結果比其他參數高，因為其不包含原始數據參數信息等。

從實驗結果可以得到：

(1) 新模型可保持原模型訓練參數、知識結構等信息，不需要對原數據重復訓練。

(2) 保存原數據信息的同時能對新進數據進行特征學習，滿足大數據實時性要求，具有很好的拓展適應性。

4 結 語

本文針對大數據變化特征、異構特征等做了分析與研究，發現現有模型大部分基于向量空間表示學習，無法滿足大數據實時性要求，存在局限性。為了解決此類問題，本文設計遞增式迭代深層學習模型，分析與歸納該模型的關鍵問題，設計后向傳播方法、近似一階導方法更新參數和結構等方法。實驗證明，該模型能保持原參數等信息不變的同時繼續學習新進數據特征，并且不需要對原始數據重新訓練，設計基于高維張量空間表示的反向算法，將向量空間拓展到張量空間，適應了大數據變化需求，提高模型計算效率，滿足了當下大數據要求。