基于數據空間網格化的密度峰值聚類算法

【摘要】密度峰值聚類方法能夠對數據進行聚類，且適用于任意形狀數據集的聚類。但當數據量增大時，算法的時間復雜度和存儲開銷也會大幅增加。針對此問題，提出一種基于數據空間網格化的密度峰值聚類方法，將數據每個維度的對應值域等分為若干區間，即將數據空間分成若干網格，在計算局部密度和距離時，僅需利用相鄰網格的點。實驗表明，該方法在保證聚類質量的前提下能極大地減少計算時間和占用內存，具有較高的可靠性和有效性。

【關鍵詞】密度峰值;網格化;聚類;數據空間

〔中圖分類號〕TP183 〔文獻標識碼〕A 〔文章編號〕1674-3229（2021）04-0019-05

0 引言

聚類算法是根據數據的相似性，把相同或者具有相似特征的數據劃分成同一組進行特征分析，用于數據的進一步挖掘。目前，聚類算法被廣泛應用于電子商務、社區檢測以及圖像分割等方面[1]。但大多數聚類算法都存在著聚類中心確定困難、聚類精度低、數據集自適應性不高，導致聚類效率低下和參數依賴性等問題。針對這些問題，2014年，A.Rodriguez等[2]首次提出了密度峰值聚類（DensityPeak Clustering，DPC）算法，該算法結合密度和距離兩個維度選擇出聚類中心，且不需要任何迭代。此后，學者們對DPC方法進行了一些改進，如R.Mehmood等提出了一種模糊CFSFDP方法[3]，可有效而自適應地選擇聚類中心;其他學者根據高斯分布的3B原則[4]，每個點的影響半徑為3σ（其中σ是數據點的標準差），使用數據的潛在嫡自動計算截斷距離dc，提高聚類效果[5-6];高詩瑩等[7]通過計算數據樣本中的密度比，減少密度較小類簇的遺漏，提高聚類精度;Shuliang Wang等[8]使用多變量的核密度估計方法自動選擇截斷距離dc;Rashid Mehmood等[9]基于熱方程，使用另一個非參數密度估計器進行密度估計;Z.Yan等[10]提出基于點與第k個最近鄰點之間的距離（稱為半徑）來估計每個點的局部密度，同時利用兩個點的k個最近鄰點的交點較小，分配不同的聚類特性，改進了DPC算法的分配策略：在KNN核密度估計（NKD）[11]的啟發下，Geng YA等[12]利用相對k最近鄰核密度（RNKD）來估計點的密度，解決了NKD在類密度不均勻的情況下聚類性能不佳的問題，設計了RECOME算法。

DPC在聚類過程中，需要計算每個數據點的局部密度和每個數據點與其他較高局部密度點之間的最短距離，其時間復雜度為O（N2），存儲開銷為O（1/2N2）。對于大規模數據集，為提高效率，ShichaoCheng[13]等提出了FDP算法，使用k-dtree建立指標索引，只計算當前點的k個最近鄰。王飛等[14]提出了基于網格的密度峰值聚類算法（GDPCA）。該算法根據數據集的分布，按照一定的規則自適應地劃分網格，并將數據按照規則映射到網格空間中，然后對每個網格空間的數據使用密度峰值聚類算法進行聚類分析，接著根據邊界點的分布進行相鄰網格聚類結果的合并，其不足之處在于沒有利用距離這個維度，在一些數據集上無法達到令人滿意的效果。Courjault-rad等在2016年提出IDPC算法[15]，通過使用縮小窗口（ICMDW）迭代封面圖來構建密度圖，從而減少維度，但當局部密度較高時，迭代次數會急劇增加。

本文提出的基于數據空間網格化的密度峰值聚類（LSDPC）算法利用相鄰網格所在的點計算密度，而不必基于所有全局數據點兩兩之間的距離來計算密度;最后得到的決策圖是全局數據點的決策圖，而不必像文獻[14]再進行各個網格聚類結果的合并;在保證聚類質量的前提下，極大地減少了計算時間和內存的開銷。

1 密度峰值聚類（DPC）算法

密度峰值聚類算法中，聚類中心的確定需要給出樣本點的局部密度ρ和兩個樣本點之間的距離δ。假設待聚類的數據集s={xi}i=1N，數據點xi和xj之間的距離可以表示為dij=dist（Xi，Xj）。定義S中任意數據點xi的兩個參數為ρi和δi，ρi表示當前點的局部密度，δi表示密度大于當前點且離當前點最近的距離。使用截斷核函數來定義數據點Xi的局部密度ρi，其表達式如下：其中參數dc為截斷距離（Cut-off distance）。定義Xi與Xj之間的最小距離δi為：

在計算δi的時候同時記錄ρ值更大的數據點中與第i點距離最近的點的編號j，記做L（i）。

計算綜合考慮ρ值和δ值的聚類決策值γi，用來確定一個聚類中心，如式（3）

γi=ρiδi，i∈IS（3）

DPC算法的具體步驟如下：

DPC算法的瓶頸在于計算數據點的密度時，要利用所有數據點間的距離進行密度值的計算。一種做法是引入一個（對稱的）距離矩陣，用來存儲數據集中的任意兩個點之間的距離，但是這種方法的時間復雜度為O（N2），且需要O（1/2N2）的存儲開銷。

對于樣本點的局部密度ρi的計算，需要求出Xi和其他樣本點之間的所有距離dij{j=1…N，j≠i}。因此，ρ的計算復雜度為O（N2）。

對于兩個樣本點之間的距離δi，需要對所有的ρ進行排序，并查找比較大于ρi的所有點的距離。因此，δ的計算復雜度為O（1/2N2）。

2 基于數據空間網格化的密度峰值聚類算法

2.1 問題分析

用DPC算法計算局部密度ρi耗時較長，當數據量增大時，這個問題尤為突出。有效計算局部密度ρi的瓶頸在于要求出Xi和其他樣本點之間的所有距離dij{j=1…N，j≠i}。實際上，隨著樣本點的距離越近，它對局部密度ρi的貢獻越大，而其他點對密度的貢獻隨著到目標點的距離增大而呈指數衰減。據此，本文將樣本在n維空間進行劃分，對每一個維度等量劃分，將全空間劃分為互不相交的網格單元。如圖1所示，在二維數據的情況下，對于圓點所在的編號14的網格，本文只需要將上下左右以及斜線上的8個相鄰網格以及自身網格（編號為8，9，10，13，14，15，18，19，20）中點集合做密度計算，求近似值即可。只需搜索相鄰網格的局部點來近似計算局部密度，不用對所有數據點間的距離進行排序，避免樣本點對上的重復計算。

圖1 二維空間網格化

同樣，對于兩個樣本點之間的距離s，只考慮相鄰網格的點即可。因為距離最近的點一定在相鄰的網格中，只需查找這些網格中密度ρj比它大的點即可。如果不存在密度比它大的點，說明該點是局部密度最大，可以參加第二次的全局密度比較。

該相鄰網格計算法顯著降低了原始DPC算法中密度計算成本，卻獲得了幾乎相等的聚類效果。圖2第一列展示了數據集flame上，DPC算法截斷距離dc=4%的情況下以及LSDPC算法截斷距離dc=8%、網格數為5×5情況下的聚類結果和決策圖。圖2第二列展示了數據集S2上，DPC算法截斷距離dc=4%的情況下以及LSDPC算法截斷距離dc=8%、網格數為88×88情況下的聚類結果。

圖2 Flame和S2數據集上DPC和LSDPC的聚類結果比較

2.2 算法步驟

LSDPC算法步驟如下：

2.3 計算復雜度分析

假設樣本數為N，則ρ的計算復雜度為O（N2），δ的計算復雜度為O（1/2N2）。分成m個網格后，則每個網格平均有N/m個點，對每個網格來說，有k個鄰居，ρ的計算復雜度為（kN/m）2，全部的計算復雜度為m*（kN/m）2=k2*N/m*N。根據歸納總結則計算復雜度為O（kN）。

同樣可以求得δ的計算復雜度為O（kN）。

3 實驗分析與討論

3.1 評價指標

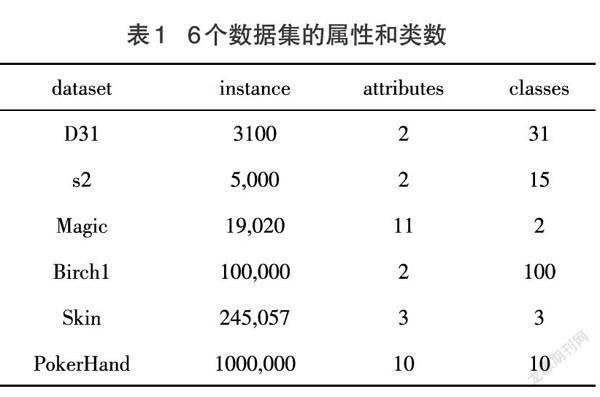
為了驗證本文算法的性能，使用了6個模擬數據集，每個數據集的屬性數量和類數如表1所示。

表1 6個數據集的屬性和類數

為了客觀評價比較聚類算法，本文從三個方面來評估：內部評價指標、外部評價指標和運行時間[16]。內部評價指標使用戴維森堡丁指數（Da-vies-Bouldin Index），DB越小意味著類內距離越小，同時類間距離越大，聚類效果越好。外部評價指標使用調整蘭德指數（Adjusted Rand index ARI），ARI考慮到同一個聚類和不同聚類中存在的實例數。ARI取值范圍為[0，1]，值越大意味著聚類結果與真實情況越吻合。值為1的時候代表所有的樣本都被正確地聚類，每個聚類只包含本類樣本。從廣義的角度來講，ARI衡量的是兩個數據分布的吻合程度。

3.2 實驗結果比較

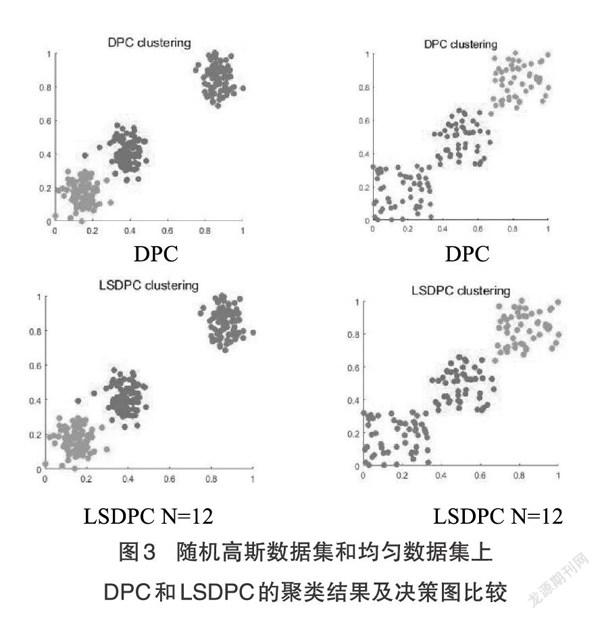
為了驗證算法的有效性，首先在隨機生成的包含三類的高斯數據集及隨機生成的包含二類的均勻分布的數據集上進行比較。圖3分別展示了高斯數據集和均勻數據集的聚類效果。可見兩者算法都能達到較好的聚類效果，并且都能從決策圖上識別出聚類中心。

圖3 隨機高斯數據集和均勻數據集上DPC和LSDPC的聚類結果及決策圖比較

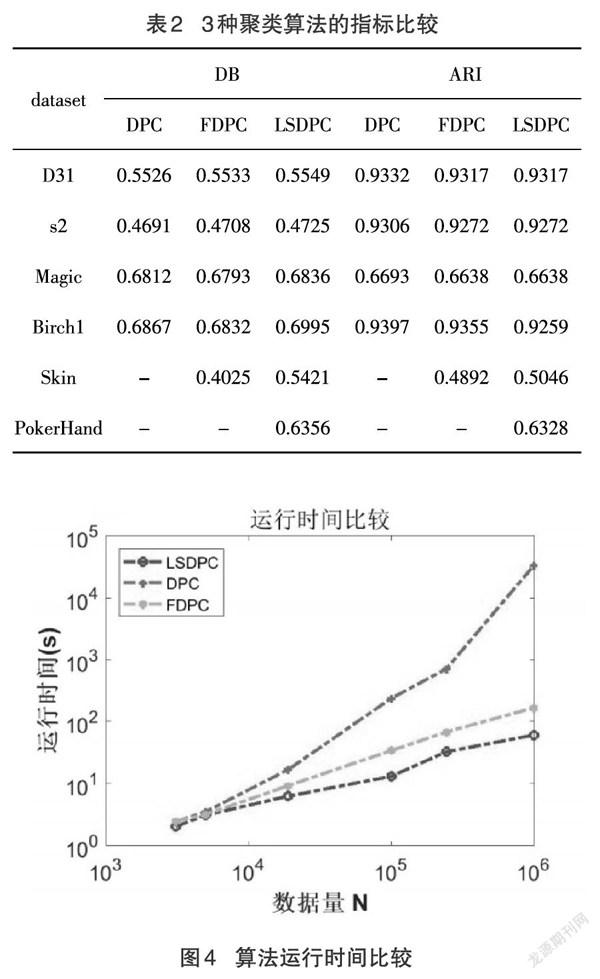
表2展示了DPC、FDPC[13]、LSDPC在6個數據集上的DB、ARI指標結果。對于每個聚類算法，每個度量的最佳值都以粗體顯示。而“-”代表無法度量，內存溢出。

從表2可以看出LSDPC算法與DPC、FDPC聚類算法相比，LSDPC算法在6個數據集上，基于所有外部度量提供了最佳的聚類輸出。

表2 3種聚類算法的指標比較

圖4算法運行時間比較

圖4顯示了三種聚類算法的運行時間比較結果。當N=104時，LSDPC使用的時間與FDPC相差不大;相比于DPC，LSDPC節省了1個數量級。當N=106時，LSDPC使用的時間相比于FDPC節省了一個數量級;對比DPC，LSDPC節省的時間將達到3個數量級。結合表2可以看出，LSDPC在聚類指標（ARI、DB）上十分接近DPC，而且隨著數據量的增大，指標值更為接近。雖然LSDPC在聚類指標ARI上略低于DPC，但可以極大地減少運行時間。

4 結論

本文針對在大規模數據聚類時，DPC算法所需時空代價急劇增大的問題，提出了數據空間網格化的密度聚類方法。LSDPC算法將數據每個維度對應值域等分為若干區間，將數據空間分成若干網格，同時僅利用相鄰網格所在的點計算局部密度和距離。文中將LSDPC在6個數據集上作了實驗，并從ARI、DB、運行時間三個方面對LSDPC結果進行分析比較。當數據量增大時，該方法對比DPC來說，極大地降低了算法的時間和內存消耗。例如，當原始數據樣本點數大小超過100，000時，所提算法仍能在可承受的時間和內存中執行。但本文實驗中的網格數目采用經驗方法來確定，今后可根據不同的數據集來確定網格數目，改進算法，以提高聚類算法的準確性。

[參考文獻]

[1]Olfa Nasraoui，Chiheb-Eddine Ben N'Cir.Clustering Meth-ods for Big Data Analytics[M].Switzerland：Springer，Cham，2019.

[2]Rodriguez A，Laio A.Machine learning.Clustering by fastsearch and find of density peaks[J].Science，2014，344（6191）：1492.

[3]Mehmood R，Bie R，Dawood H，et al.Fuzzy Clustering byFast Search and Find of Density Peaks[J].Personal&Ubiq-uitous Computing，2016，20（5）：785-793.

[4]Barany I，Vu V H.Central limit theorems for Gaussian poly-topes[J].Annals of Probability，2006，35（4）：1593-1621.

[5]Ji C，Lei Y.Parallel clustering by fast search and find ofdensity peaks [A].2016 International Conference on Au-dio，Language and Image Processing（ICALIP）[C].NewYork：IEEE Xplore，2017：563-567.

[6]Wang S，Wang D，Caoyuan L 1，et al.Clustering by FastSearch and Find of Density Peaks with Data Field[J].Chi-nese Journal of Electronics，2016，25（3）：397-402.

[7]高詩瑩，周曉鋒，李帥.基于密度比例的密度峰值聚類算法[J].計算機工程與應用，2017，53（16）：10-17.

[8]WANG Shuliang，WANG Dakui，LI Caoyuan，et al.Cluster-ing by Fast Search and Find of Density Peaks with DataField[J].Chinese Journal of Electronics，2016，25（3）：397-402.

[9]Mehmood R，Zhang G，Bie R，et al.Clustering by fastsearch and find of density peaks via heat diffusion[J].Neu-rocomputing，2016（208）：210-217.

[10]Yan Z，Loo W，Bu C，et al.Clustering spatial data by theneighbors intersection and the density difference[A].2016 IEEE/ACM 3rd International Conference on Big DataComputing Applications and Technologies（BDCAT）[C].New York：IEEE Xplore，2016：217-226.

[11]Tran T N，Wehrens R，Buydens L M C.KNN-kerneldensity-based clustering for high-dimensional multivari-ate data[J].Computational Statistics&Data Analysis，2006，51（2）：513-525.

[12]Geng Y A，Li Q，Zheng R，et al.BECOME：a New Densi-ty-Based Clustering Algorithm Using Relative KNN Ker-nel Density[J].Information Sciences，2018：13-30.

[13]Shichao Cheng，Yuzhuo Duan，Xin Fan，et al.Review ofFast Density-Peaks Clustering and Its Application to Pedi-atric White Matter Tracts[J].Medical Image Understand-ing and Analysis，2017：436-447.

[14]王飛，王國胤，李智星，等.一種基于網格的密度峰值聚類算法[J].小型微型計算機系統，2017，38（5）：1034-1038.

[15]Vincent Courjault-Radé，Ludovic D'Estampes，St6phane Pu-echmorel.Improved density peak clustering for large datasets[EB/OL].https：//hal.archives-ouvertes.fr/hal-01353574，2016-12-12.

[16]Zhang Y，Cheny S，Yu G.Efficient Distributed DensityPeaks for Clustering Large Data Sets in MapReduce[A].2017 IEEE 33rd International Conference on Data Engi-neering（ICDE）[C].New York：IEEE Xplore，2017：67-68.

[收稿日期]2021-07-28

[基金項目]莆田學院科研項目“基于張量數據的顯著性檢測算法研究”（2016041）

[作者簡介]張萍（1982-），女，碩士，莆田學院機電與信息工程學院講師，研究方向：計算機視覺、機器學習。