基于CNN的圖像分類中激活函數的研究

張琴

（福州職業技術學院信息技術工程系，福州 350108）

0 引言

2012年Hinton教授小組在ImageNet視覺識別競賽[1]中通過卷積神經網絡（CNN）將錯誤率從原來的25%降到了16%之后，CNN的應用越來越廣泛，主要包括計算機視覺、自然語言處理、語音識別等領域[2]。激活函數作為CNN中的一個重要模塊，不僅為卷積神經網絡提供了學習復雜分布所必需的非線性，而且可以有效抑制殘差衰減并提高收斂速度，這也是CNN取得成功的關鍵[3]。研究者對CNN的研究工作高度重視，但其中存在一些困難和問題仍然沒有很好的解決方法。例如，在網絡結構設計和模型訓練方面尚未形成通用的理論，需要依靠經驗并花費大量時間進行調試，不斷探索優化算法和最佳的參數；反向傳播算法中存在“梯度消失”、“神經元壞死”等現象，導致模型無法進行有效的訓練。本文通過分析各種常用激活函數的優缺點，結合激活函數在訓練過程中的作用，給出激活函數在設計時需要考慮的要點，據此設計出了一種新的非線性非飽和的激活函數SReLU，該函數兼具Softplus函數和ReLU函數的優點，具有較強的表達能力和稀疏能力[4]，且收斂速度快，識別率高。

1 常見的激活函數及特征

1.1 飽和非線性激活函數

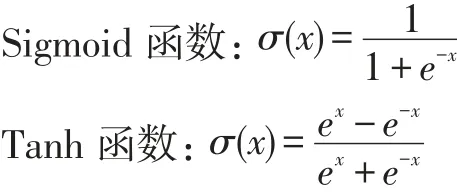
Sigmoid函數及其導數的圖像如圖1所示，從函數圖像可以看出該函數能夠把輸入的連續實值變換為0和1之間的輸出，即輸出恒為正值，不是以零為中心的，這個特性會導致后面網絡層的輸入也不以零為中心，從而影響收斂速度。x為0附近的值時，激活函數對信號增益效果明顯，但是當|x|的取值越來越大時，σ'(x)越來越小，容易導致梯度消失。Tanh函數也是一種常用的S型非線性激活函數，函數及其導數的圖像如圖2所示，它是Sigmoid函數的改進版。Tanh函數克服了Sigmoid非0均值輸出的缺點，收斂速度較快，但是仍然無法解決梯度彌散的問題。由于這兩個函數本身及其導數的計算都是指數級的，計算量相對較大。

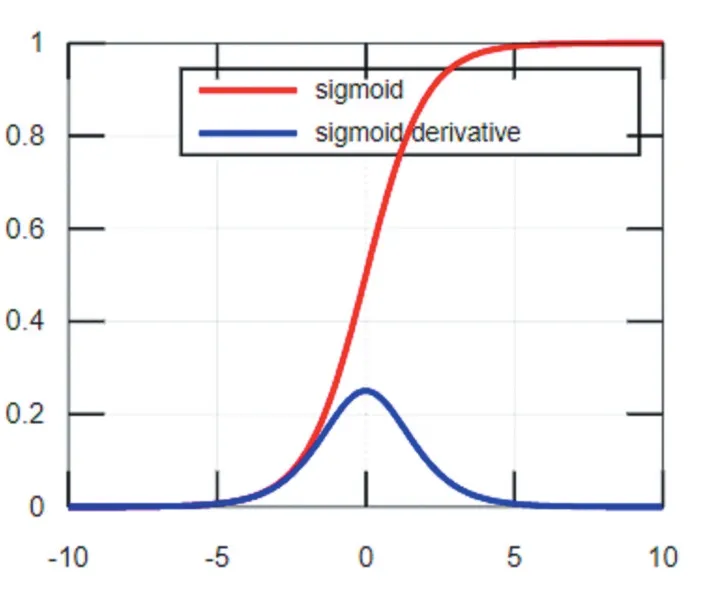
圖1 Sigmoid函數及其導數

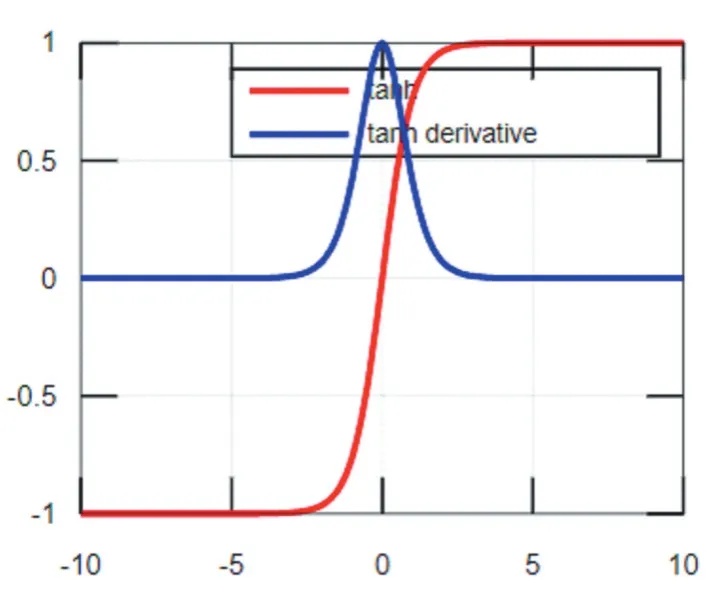
圖2 Tanh函數及其導數

1.2 非飽和非線性激活函數

ReLU函數：σ(x)=max(0,x)

Softplus函數：σ(x)=ln(ex+1)

ReLU函數及其導數的函數圖像如圖3所示，由圖可知ReLU函數具有分段線性性質，因此其前傳、后傳、求導都具有分段線性，相比于傳統的S型激活函數，ReLU收斂速度更快。當輸入值小于0時，ReLU函數強制將輸出結果置為0，使訓練后的網絡模型具有適度的稀疏性，降低了過擬合發生的概率，但是稀疏性使模型有效容量降低，從而產生“神經元壞死”現象[5]，導致模型無法學習到有效特征。Softplus是對ReLU近似光滑的一種表現形式，其函數圖像如圖4，它不僅可以把輸入的數據全部進行非線性的映射，而且不會把一些有價值的信息隱藏掉，但是用Softplus函數作為激活函數，收斂速度很慢。

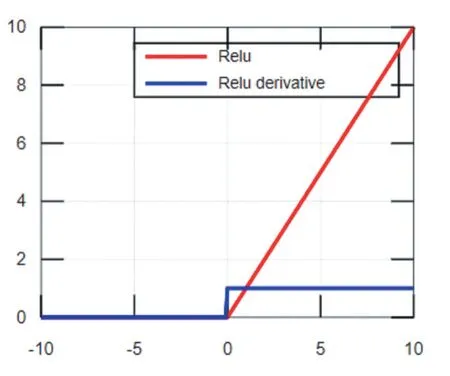
圖3 ReLU函數及其導數

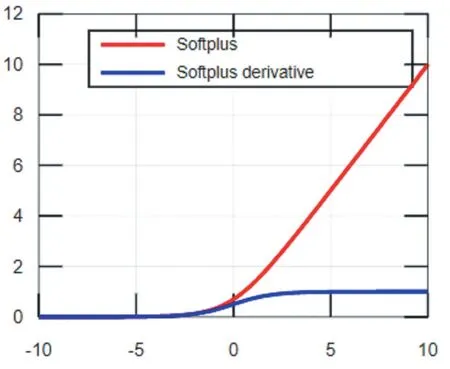
圖4 Softplus函數及其導數

2 激活函數設計方法分析

前向傳播和反向傳播是卷積神經網絡模型訓練的兩個主要步驟。前向傳播是指數據從低層向高層傳播，從輸出層輸出結果的過程。當前向傳播得到的結果不符合預期的時侯，開始執行將誤差從高層向低層傳播訓練，推導參數的學習規則，迭代改變參數，直到誤差損失滿足設定的精度的過程。通過對卷積神經網絡訓練過程進行分析，可以更好的理解激活函數在模型訓練中的作用，幫助我們選擇更加適合的激活函數。

（1）在前向傳播過程中，對卷積層每一種輸出的特征圖xj有：

式中Mj表示選擇輸入特征圖組合，σ是激活函數，是卷積核，bj是第j種特征圖的偏置。由式（1）可知，在前向傳播過程中，激活函數對上一層卷積操作的結果進行非線性變換，增強特征的表達能力。所以激活函數必須為非線性函數，此外，為了模型的訓練速度，激活函數的計算應盡可能簡便。

（2）反向傳播的主要任務是對卷積核參數k和偏置b進行優化。根據BP算法，將損失函數分別對卷積核參數k和偏置b求偏導然后乘以學習率，可以得到參數的變化量Δk和Δb。誤差代價函數對卷積核k求偏導：

誤差代價函數對偏置b求偏導：

由（1）到（3）式可知，激活函數在卷積神經網絡前向傳播和反向傳播中均起到巨大作用。在選擇激活函數時應綜合考慮激活函數自身及其導數的特點，具體如下：①激活函數必須為非線性函數。②激活函數自身及其導數的計算不可過于復雜。③為了保證網絡參數能正常更新，應盡量避免選擇軟飽和激活函數，即具有性質的激活函數。④為了加快模型的收斂速度，參數的更新方向不應該被限制。選擇一個取值即可以為正數也可以為負數的激活函數，可以加快收斂，參數更新也更加靈活。

3 改進的激活函數SReLU

改進后的激活函數SReLU是一種非線性非飽和的激活函數，兼具Softplus函數和ReLU函數的優點。在大于0的部分使用ReLU激活函數；為了激活負值，在小于0的部分，使用向下平移ln2個單位的Softplus激活函數。SReLU表達式為：f(x)=max(ln(1+ex)-ln2,x)，函數圖像如圖5所示，SReLU激活函數保留了ReLU函數收斂快的優勢，同時激活了負值，向前一層傳播的信息也更多，緩解了“神經元死亡”的現象。

4 試驗及結果分析

為了驗證提出的SReLU激活函數在不同數據集中的有效性，分別在數據集MINIST和CIFA-100中使用SReLU及其他常見的激活函數進行訓練分析。本試驗基于Keras深度學習框架，通過損失函數下降曲線和在訓練集、測試集、驗證集上的準確率分析實驗的運行狀態。最終的實驗結果表明：在MINIST和CIFA-100這兩個數據集中使用SReLU激活函數均能夠達到比其他常用激活函數更快的收斂速度和更高的準確率。

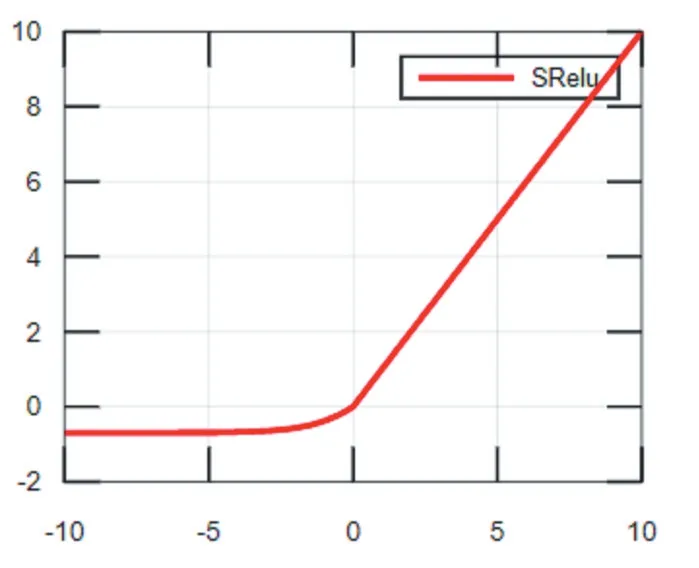
圖5 SReLU函數

4.1 在MINIST數據集上實驗結果及分析

MINIST數據集是一個簡單的手寫數字數據集，該數據集包含70000張28×28像素的灰度手寫數字圖片[7]。本次針對MINIST數據集的試驗設計的網絡模型結構由2個卷積層，1個池化層，1個全連接層和一個輸出層組成。第一個卷積層通道數為32，Filter大小為3×3，，卷積步長為1。第二個卷積層通道數為64，Filter大小與卷積步長與第一個卷積層相同。池化層Filter大小為2×2，全連接層神經元個數為128，輸出層使用Softmax回歸，學習率設為0.001。實驗結果準確率如表1所示，由表1可知，相比于經典的激活函數，提出的激活函數SReLU在訓練集、測試集和驗證集上均具有最高的精度。實驗損失函數下降曲線如圖6所示，在整個訓練過程中Sigmoid函數的損失率最高，ReLU函數在前1000次迭代中損失下降最快，之后SReLU函數迭代損失下降速度逐漸高于ReLU，最終SReLU函數的損失最小，說明在MINIST數據集上基于SReLU激活函數的模型分類性能最好。

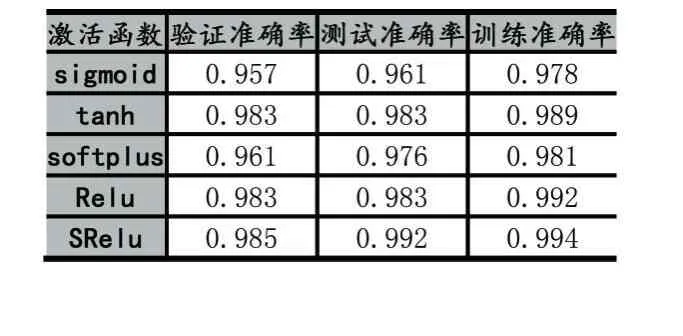
表1 SReLU在MINIST數據集上的準確率

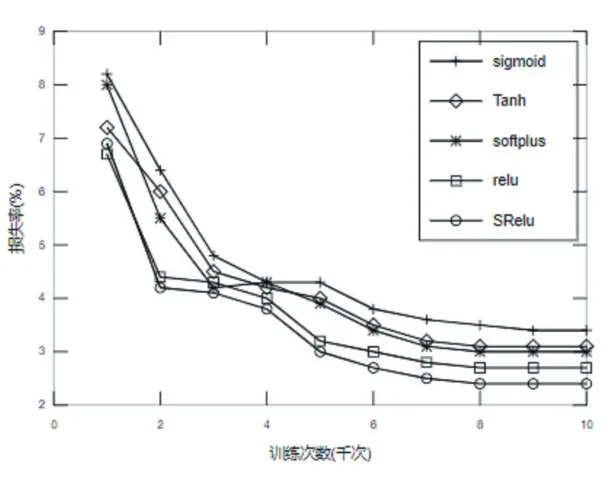
圖6 SReLU在MINIST數據集上的損失率

4.2 在CIFA-100數據集上實驗結果及分析

CIFAR數據集是一組用于普通物體識別的數據集，該數據集由來自100個分類的60000張32×32像素的彩色圖片組成，每個分類包含500個訓練樣本和100個測試樣本[8]。本次針對CIFAR-100數據集的試驗設計的網絡模型結構由4個卷積層，2個池化層，1個全連接層和一個輸出層組成。第一、二個卷積層通道數為64，第三、四個卷積層通道數為128，四個卷積層Filter大小均為3×3，卷積步長均為1。2個池化層Filter大小均為2×2，全連接層神經元個數為512，輸出層使用Softmax回歸，學習率設為0.001。實驗結果準確率如表2所示，由表2可知，在CIFA-100數據集上，相比于常見的激活函數，提出的激活函數SReLU在訓練集、測試集和驗證集上均具有最高的精度。實驗損失函數下降曲線如圖7所示，由圖可知，相比于其他激活函數，SReLU函數在前2000次迭代中就達到了最快的收斂速度，最終SReLU函數的損失最小，說明在CI?FA-100數據集上基于SReLU激活函數的模型分類性能最好。

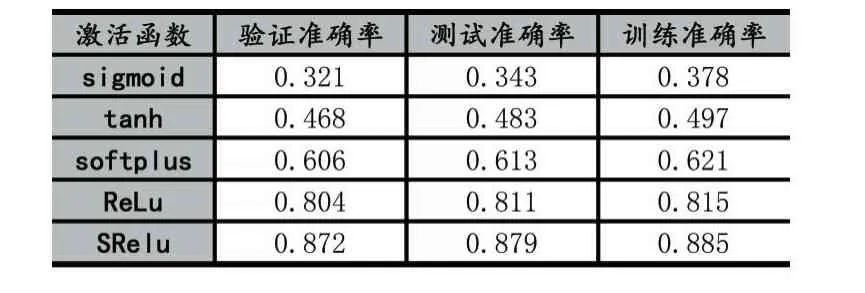
表2 SReLU在CIFA-100數據集上的準確率

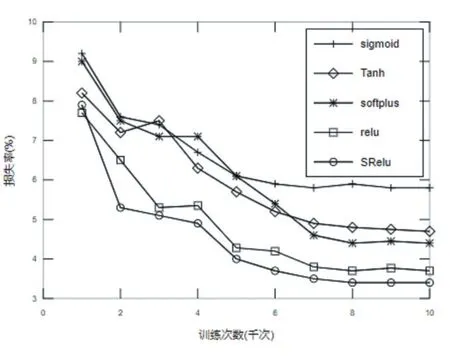
圖7 SReLU在CIFA-100數據集上的損失率

5 結語

激活函數是卷積神經網絡模型的重要組成部分，“激活的神經元”使卷積神經網絡具備了分層的非線性特征學習能力。首先通過分析激活函數在前向傳播和反向傳播中的作用，給出了激活函數本身及其導數需要具備的一些特性，然后針對卷積神經網絡中經典激活函數存在“梯度消失”、“神經元壞死”或不易收斂等缺陷，設計了一種新的非線性非飽和的激活函數SRe?LU，該函數保留了ReLU函數收斂快的優勢，同時激活了負值，緩解了“神經元死亡”的現象。