基于優化磁鏈觀測器的直接轉矩調速系統研究

紀澤宇

(安徽理工大學 電氣與信息工程學院，安徽 淮南 232001)

0 引言

在過去的10年中，直接轉矩控制(Direct Torque Control，DTC)在感應電動機的交流變頻器領域得到了積極的研究.這種控制策略最初是由Takahashi于1986年提出的，與此同時Depenbrock在1988年以直接自我控制的名義發展，并向弱磁調速方向推廣[1].

直接轉矩控制理論是在矢量控制基礎上發展的，雖然在原理上矢量比標量好，但實際上，因為轉子的磁鏈難以估算和復雜的矢量變換影響，使得實現實際控制的預期效果變得困難[1].而DTC不存在矢量控制的問題,DTC的主要優點是可以實現高性能(去耦控制定子磁通和轉矩，快速轉矩響應和魯棒性)及方案的簡單性(不需要坐標轉換，調制模塊和電流調節模塊)，對其進行深入研究可以更適應現代快速發展的電子技術[2].

本文從直接轉矩控制的基本原理和感應電機的多變量數學模型入手，首先通過Matlab建立了一個直接轉矩調速系統仿真模型，并對系統各模塊作了說明，且對磁鏈觀測器進行了優化;然后，驗證了此磁鏈觀測器下的異步電動機直接轉矩控制的良好動靜態性能和較強的抗干擾能力.

1 異步電機的數學模型

在α-β坐標系下，理想狀態下的等效電路圖[3]如圖1所示.

圖1 異步電機的等效電路圖

由圖1可以得出兩相坐標下的電機數學模型，并得出以下方程.

定子電壓方程：

(1)

轉子電壓方程：

(2)

由上面兩個式子可以得到電機在兩相坐標系下的電壓方程：

(3)

其中：Lr=Lrl+Lm，Ls=Lsl+Lm;p為微分算子.

由電磁關系，可以列出電機的磁鏈方程：

(4)

異步電機的轉矩方程：

Te=pnLm(isβirα-isαirβ).

(5)

將從式(4)得到的irα和irβ帶入(5)，得：

Te=pnLm(isβirα-isαirβ)=pn(ψs?is).

(6)

再將(4)中可得到的isα和isβ表達式代入(6)中，可得到以下方程式：

(7)

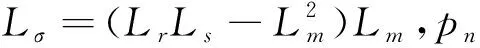
異步電機的運動方程為：

(8)

2 直接轉矩控制原理

直接轉矩控制(DTC)的理念是以轉矩為原點來整合所有控制，除了能控制轉矩，同時也可以控制磁鏈量.它的實質是通過空間矢量概念對定子磁鏈定向,并經過較易檢測到的定子電壓和電流等量,直接在定子坐標系下計算與控制電動機的磁鏈和轉矩，其控制原理框圖如圖2所示[4].

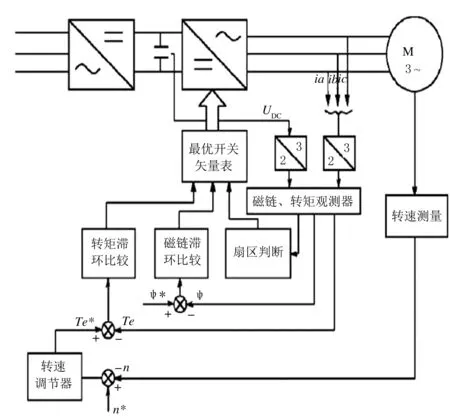
圖2 異步電機直接轉矩控制框圖

從圖2中，可以看出對應于定子磁通和轉矩的大小存在兩個不同的回路.將磁通定子模量和轉矩的參考值與實際值進行比較，并將得到的誤差值分別饋入兩級和三級磁滯塊，εФ和ετ信號被輸送到2個滯后比較器，之后相應的數字化輸出變量磁通量Δ，轉矩 Δτ和定子通量位置扇區，再從表1選擇合適的電壓矢量.該選擇產生脈沖Sa、Sb、Sc來控制電源中的電源開關，從而驅動異步電動機[5].

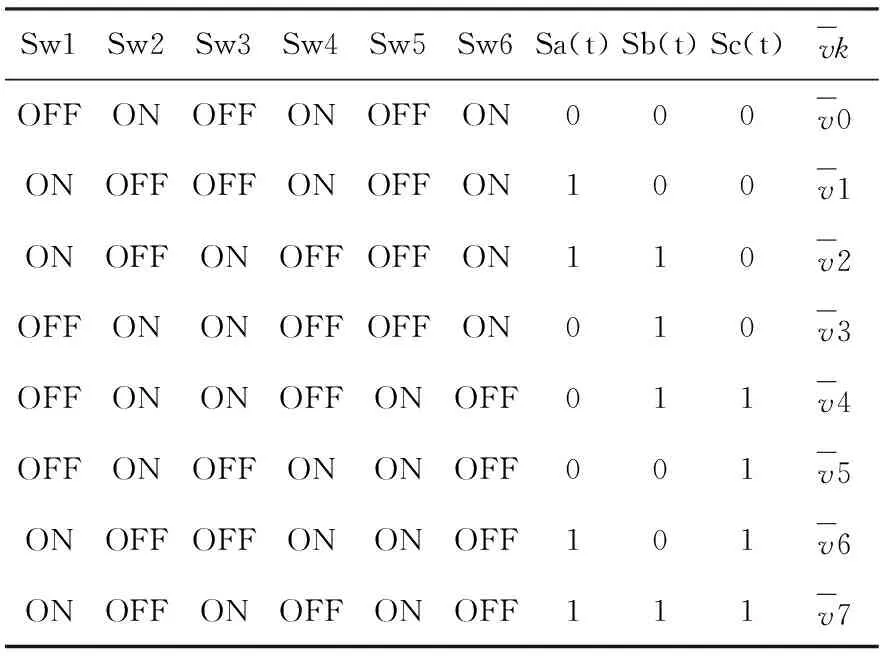
表1 開關狀態選擇

3 異步電機直接轉矩控制系統建模

本系統主要功能由逆變模塊、控制模塊、3/2變換模塊幾大部分組成.下面介紹各個部分的功能及電路構成.

3.1 逆變模塊

選用三相橋式逆變模塊，如圖3所示.逆變器模塊是系統的開關控制結構，用于執行輸出的PWM波形，可采用系統自帶的通用橋模塊或自行搭建逆變器模塊，本文采用的逆變器模塊結構如圖4所示.

3.2 定子磁鏈3/2變換模塊

定子磁鏈3/2變換模塊如圖4～圖5所示，將Uabc，Iabc參數通過模塊變換為Usα、Usβ、Isα、Isβ.

圖4 3/2電壓變換模塊

圖5 3/2電流變換模塊

3.3 磁鏈觀測模塊

定子磁鏈的估測模型可以分為兩種：電壓模型和電流模型.

電壓模型磁鏈觀測器結構簡單，利用電機反電動勢計算得到電機的定子磁鏈，電機運行在中高速區時，可以準確得到磁鏈觀測值，但是因為定子電阻壓降的存在會在轉速比較低時引入較大的誤差；電流模型磁鏈觀測器在低速時可以使用，比電壓模型精確，但在高速時比不上電壓模型[6].所以兩種模型可以結合起來運用，可以獲得精確的定子磁鏈Ψs.此模型的磁鏈觀測器如圖6所示.

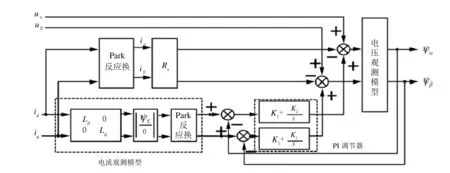
圖6 基于結合模型的磁鏈觀測器

由圖7可知，定子磁鏈表達式為:

(9)

式中:φs表示總磁鏈觀測值;φsc、φsv表示定子磁鏈值，φsc和φsv兩項的系數和為1.

定義φsv的系數為H(s)，如式(10)所示:

(10)

式(10) 所示的函數可視為電壓模型觀測到的定子磁鏈占總磁鏈觀測值的權重函數. 若K1、K2為無窮大，則模型為電流模型;若K1、K2為零，則模型為電壓模型[7].

仿真模型輸入為Usα、Usβ、Isα、Isβ，輸出為定子在α和β軸上的磁鏈分量Ψsα、Ψsβ.

3.4 轉速調節器及開關表模塊

由圖6可知，通過輸入△ω，然后通過仿真模型得出Te的給定值.

根據定子磁通和轉矩誤差信號的輸出以及圖7中的定子磁通角位置選擇合適的電壓矢量.選擇最佳電壓矢量在整個開關周期內控制定子磁通和電轉矩，將誤差保持在DTC的滯后帶內.

圖7 開關表模塊仿真圖

轉換調節器主要用來調節轉速，內部結構仿真模塊如圖8所示.

圖8 轉速調節器仿真模塊

3.5 參數設置

仿真中的主要參數如表2所列.

表2 仿真主要參數

4 仿真波形結果分析

通過對優化的磁鏈觀測器下的異步電機直接轉矩控制調速系統仿真，得到系統各性能指標的仿真波形，如圖9～圖12所示.

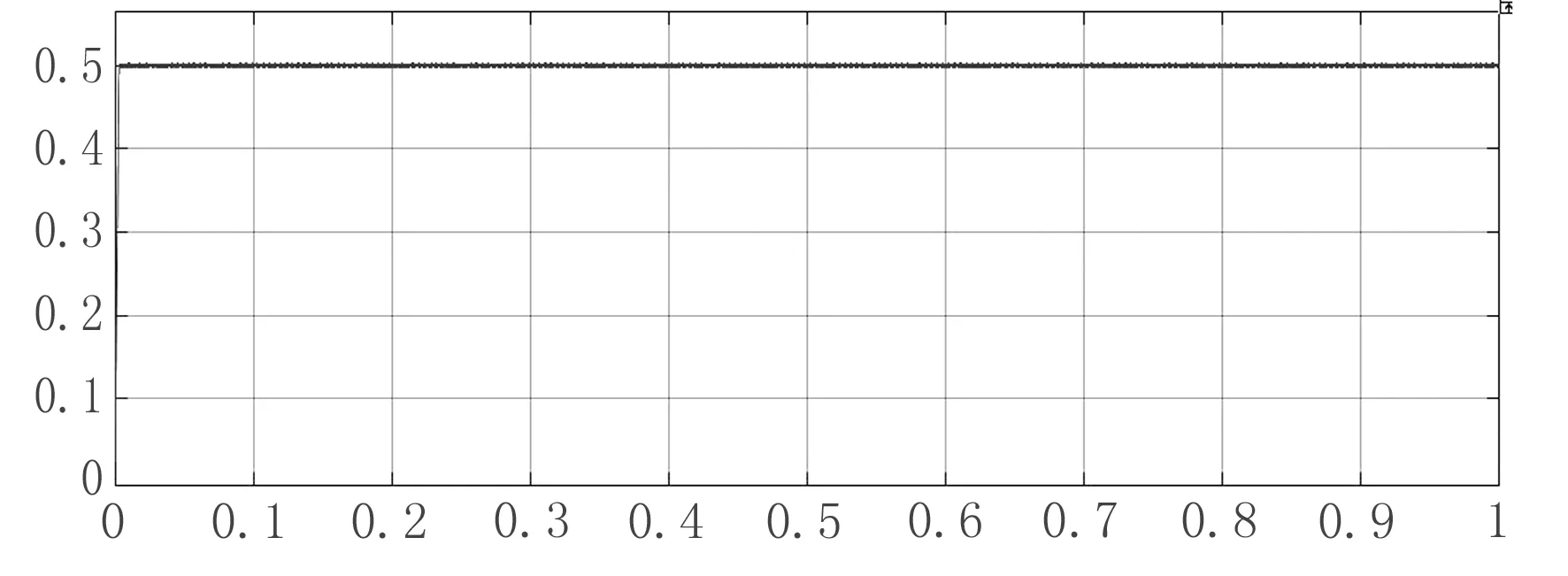
圖9 磁鏈幅值波形

由圖9得,整個系統剛開始運行時，定子磁鏈的幅值快速增加；平穩運行時，其幅值穩定在0.5 wb，表示其靜態性能良好.

由圖10轉矩波形得到在給定轉速的情況下，在系統剛運行0.01秒內波動較大，但在之后迅速進入穩態狀態，表現其動態響應快.

圖10 轉矩波形

由轉速轉矩波形圖可以看出轉速運行平穩.從圖10中可以看出在0.7 s時向系統中加入負載，瞬時轉矩變化并在此刻達到一個新的穩態點，而圖12中0.7s 時轉速幾乎沒有變化，說明系統抗干擾能力較強.

圖11 三相電流波形

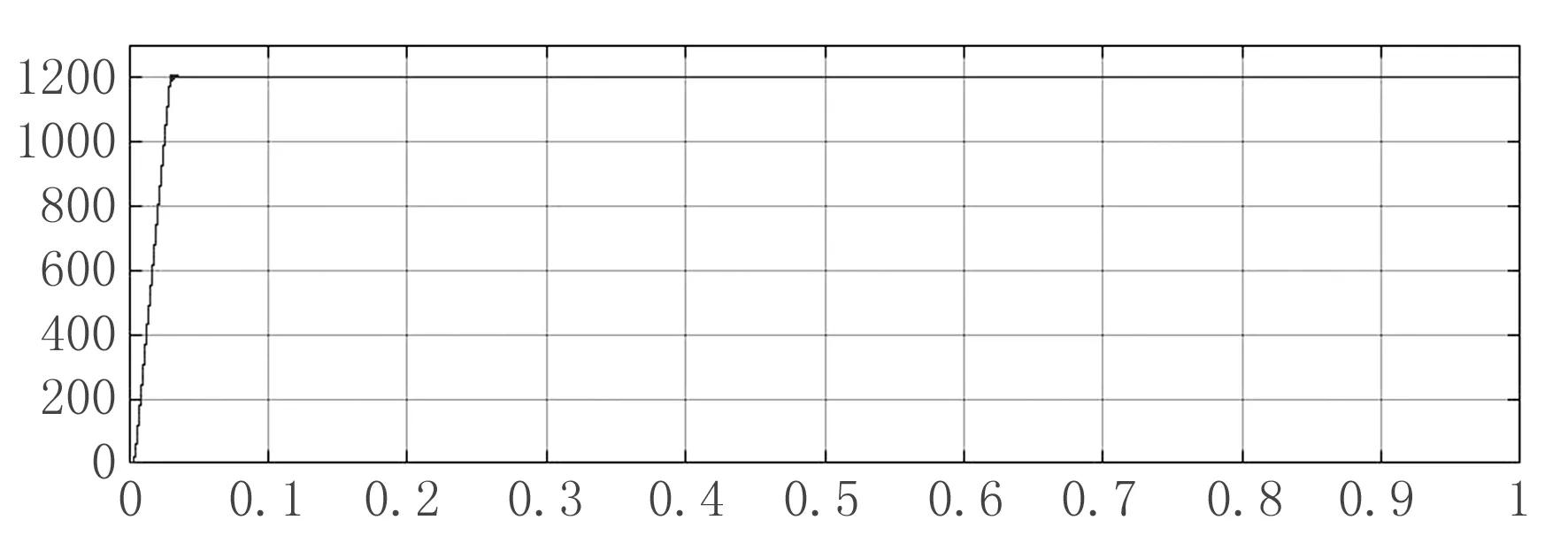
圖12 轉速波形

5 結束語

本文對定子磁鏈進行電壓和電流模型結合的優化，并利用Matlab建立了一個直接轉矩調速系統.從仿真結果看,驗證了在此磁鏈觀測器下的系統魯棒性好，穩態時轉速平穩，具有良好的動靜態性和較強的抗干擾能力.