基于軟判決下的不刪余極化碼參數識別

吳昭軍，鐘兆根，張立民，但波

（1.海軍航空大學航空作戰勤務學院，山東 煙臺 264001；2.海軍航空大學航空基礎學院，山東 煙臺 264001；3.海軍航空大學岸防兵學院，山東 煙臺 264001）

1 引言

為了對抗信道噪聲的干擾，信道編碼技術被廣泛應用于無線通信系統中。在各種信道編碼類型中，極化碼是已從理論上證明，性能可逼近香農極限的編碼，目前這種編碼已經被確定為5G 通信中eMBB 場景控制信道的編碼方案，可以預見，在不久的將來，應用了極化碼的數字通信系統會越來越多地出現，然而，針對極化碼參數識別的研究目前還未見報道，對于非合作通信領域而言，極化碼參數識別問題是一個亟待解決的問題。

目前，信道編碼盲識別問題已經是非合作通信領域研究的熱點。從公開發表的文獻來看，針對編碼識別的算法主要集中于線性分組碼、循環碼、卷積碼、Turbo 碼、LDPC（low density parity check）碼等，而單獨針對極化碼參數識別的算法還未見公開報道。針對線性分組碼而言，目前大部分算法主要基于秩準則算法[1-3]完成參數識別，這種算法計算量大，且容錯性不好；為了提高秩準則方法的容錯性，文獻[4]分析了碼字經高斯消元后，每一列上0-1分布特征，通過設定門限識別出線性相關列，從而檢測出秩虧，該方法容錯性有較大的提升，但是計算復雜度有明顯的增加；文獻[5]在高斯信道下，基于碼字之間的歐氏距離分布，對碼字進行聚類，從而識別出碼長、生成矩陣等參數，該方法適用于低碼率、短碼長下的分組碼；針對循環碼而言，目前算法主要基于其嚴格的代數結構進行識別，如基于碼重統計方法[6]、歐幾里得輾轉相除法[7]及基于多項式分解算法[8-9]等，這些方法都具有較好的工程實用性；針對卷積碼而言，文獻[10]采用迭代的高斯消元方法獲取對偶向量，由于卷積碼約束長度較短，故該方法實時性較好，同時還具有一定的容錯性；為了進一步提升文獻[10]算法的容錯性，文獻[11-13]提出基于快速Walsh-Hadarmard 變換（FWHT,fast Walsh-Hadarmard transform）的識別方法，該方法本質上是一種窮舉算法，雖然具有較好的容錯性，但是隨著約束長度增加，算法的計算復雜度呈指數增加；此外還有歐幾里得算法[14]、快速雙合沖算法[15]等，這些算法復雜度低，適用于低誤碼情況；由于Turbo 碼編碼結構較為復雜，故針對Turbo 碼識別主要分為三部分，即幀結構識別、分量編碼器識別和隨機交織識別。對于幀結構識別，文獻[16-17]充分利用了Turbo 碼的編碼結構，提出了基于差分預處理的參數識別方法，該方法能夠在信道環境惡劣的情況下，完成Turbo 碼幀同步、交織長度及碼率等參數識別，這為后續分量編碼器及交織器識別準備了條件；針對分量編碼器，文獻[18-19]構造出關于多項式系數的目標函數，然后基于梯度迭代優化的方法求解多項式系數，該方法具有較強的實用性；對于隨機交織器識別，文獻[20-21]綜合了校驗符合度方法及Turbo 碼反饋迭代譯碼的思想，提出了預估矯正識別方法，該方法具有較強的容錯性，克服了隨交織長度增加，算法性能會急劇惡化的問題；針對LDPC碼的識別，文獻[22-23]首次提出了基于高斯消元及2階、多階行消元的稀疏校驗矩陣重建方法；為了提升重建方法的容錯性，文獻[24]將LDPC 碼迭代譯碼的思想引入重建過程中，這使在有噪聲條件下，LDPC 碼重建率有較大的提高，但是計算復雜度也有較大幅度的增加。從上述分析來看，單獨針對極化碼參數識別的算法還未出現，而目前實際工程中極化碼的應用越來越廣泛，對于非合作通信而言，極化碼參數識別問題是一個亟待解決的難題。

基于此，本文提出了基于軟判決序列下的不刪余極化碼識別算法，該算法基于極化碼的編碼結構，首先給出并證明了有關極化碼碼長、信息比特與凍結比特位置的3 個定理，這3 個定理是識別極化碼參數的理論基礎；其次，引入了對數似然比（LLR,log-likelihood ratio）概念，為了檢測極化碼信息比特與凍結比特位置，詳細分析了LLR 的統計特性，基于最小錯誤判決準則，設定最優判決門限，最終實現了參數的識別。仿真結果證明了所提算法的有效性及較好的容錯性。

2 極化碼基本原理

對于一個二進制離散無記憶信道W重復使用n次，可以得到n個相互獨立的信道，然后通過某種線性變換，將其轉化為n個相互關聯的信道其中，X為信道W的輸入符號{ 0,1} ；Y為信道輸出符號，為任意實數；Yn表示Y的n維隨機向量，Xi?1表示X的i? 1維隨機向量。當n充分大時，極化信道將趨近于2 個極端，即一部分極化信道容量趨近于1，剩余部分信道容量趨近于0。在信息發送過程中，信息容量為1 的極化信道用來發送信息比特，而信道容量為0 的極化信道用來發送凍結比特（凍結比特通常為0），從而實現信息快速可靠的發送。極化碼原理包含信道合并、信道分裂兩部分，下面分別就信道合并、信道分裂及編碼方法進行簡要介紹。

2.1 信道合并過程

將n個獨立無關聯的信道合并成Wn:Xn→Yn，其中n=2m。在信道合并過程中，由于系統的信道容量不變，信道的轉移概率為

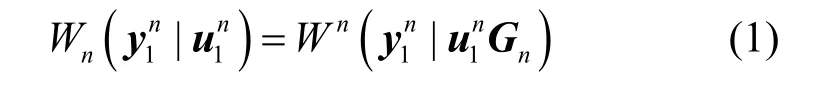
圖1 W2 信道結構

此時，W2的信道轉移概率為

其中，Bn為比特反轉置換矩陣，主要作用為將矩陣F?m的行順序按照某種規則置換。以n等于4 為例，(0,1,2,3)的二進制數為(00,01,10,11)，將其二進制反轉后得到(00,10,01,11)，對應的十進制數為(0,2,1,3)，從而得到比特反轉置換矩陣為

2.2 信道分裂過程

從信道可靠性而言，巴氏參數含義正好與信道容量相反，即Z(W)值越大，信道可靠性越差，對于巴氏參數的計算，目前有密度進化方法、高斯進化方法等，當信道為二進制刪除信道時，巴氏參數的遞推計算表達式[25]為

圖2 給出了在接收端擦除符號誤判概率為0.5下，碼長為1 024，碼率為的極化碼信道巴氏參數分布，從圖2 可以明顯看出分裂信道的可靠性趨近于2 個極端。

圖2 子信道的巴氏參數分布

2.3 極化碼編碼

由極化碼的編碼結構可知，對于不刪余極化碼盲識別而言，需要識別的參數為極化碼碼長、信息比特位及凍結比特位。由于在實際通信系統中，發送的數據都有固定的幀結構，在每一幀數據前會有2 B 的同步碼，故本文假設已經利用幀同步碼完成了碼字同步，主要的研究內容是利用軟判決序列完成不刪余極化碼碼長、信息比特位置及凍結比特位置的識別。

3 極化碼識別模型建立

3.1 極化碼碼長識別

由于極化碼碼長滿足n=2m（m為正整數）關系，故可以遍歷m的值，構造不同碼長下的碼字，然后尋找某固定的特征，實現極化碼碼長識別，在給出具體的碼長識別步驟之前，首先給出定理1 及定理2。

其中，0k×n為k×n的全零矩陣。

定理2 同樣具有遞推性，即當擴展的碼長為4n,8n,…時，碼率同樣會保持不變。

由定理1 和定理2 可知，利用截獲的序列構造不同碼長下的極化碼碼字，當碼長小于實際極化碼碼長時，該碼字對應的碼率會大于實際的極化碼碼率；反之，當碼長大于實際的碼長時，對應的碼字碼率會等于實際極化碼碼率，由此可知，在遍歷一系列碼長中，真實的碼長等于最小碼率對應的最小碼長。從上述分析可知，極化碼碼長識別的關鍵在于準確識別出不同遍歷碼長下的碼字碼率，傳統方法一般基于高斯消元方法求取碼率，但是這種方法容錯太長。從極化碼編碼原理來看，如果能識別出克羅內克矩陣中信息比特位和凍結比特位，則不僅可以間接識別出碼率，還能識別出極化碼的生成矩陣，下面重點討論極化碼信息比特位與凍結比特位的識別方法。

3.2 信息比特位與凍結比特位識別

由第2 節中極化碼的編碼原理可知，極化碼的生成矩陣中每一行向量都是克羅內克冪矩陣中行向量的一部分，故需要判斷出克羅內克冪矩陣中哪些是信息比特位置，哪些為凍結比特位置，在給出具體的識別方法之前，首先給出定理3。

從定理3 可知，為了識別出碼長為n的極化碼信息比特位，可以首先構造m克羅內克冪矩陣，其中，n滿足n=2m，然后從第1 行到第n行依次剔除克羅內克冪矩陣中行向量，然后求取其對應的對偶向量，如果對偶向量與碼字構成正交關系，剔除的位置為凍結比特位，反之則為信息比特位，從而識別出在遍歷的碼長n下，所有的信息比特位及凍結比特位，然后間接求解出碼率。由于矩陣的維度為(n? 1)×n，故的對偶空間維度為1×n，利用初等行變換與列變換可以得到

由于在信息傳輸過程中，碼字會受到噪聲的干擾，不妨設剔除的行標號為k′，則無論遍歷的位置k′是否為凍結比特位置，與碼字都不會完全構成校驗關系，此時有必要對碼字是否與構成校驗關系進行檢測，由于極化碼碼長較長，硬判決序列不可避免會造成信息的丟失，故本文利用軟判決序列來對碼字的校驗關系進行檢測。

設信號的調制方式為BPSK，即星座圖映射方式為碼元1 映射為+1，0 映射為?1。設遍歷的極化碼碼長為n′，利用截獲的軟判決序列r構造出N個碼字，則碼字矩陣T為

利用截獲的數據構造出不同碼長的極化碼，然后剔除m次克羅內克冪矩陣中第k′行元素，求解校驗向量，同時計算統計量及門限Λopt，一旦時，可以斷定位置k′為凍結信息位置，反之則判定為信息比特位置，從而實現極化碼生成矩陣的識別。

3.3 極化碼參數識別算法流程

利用3.2 節中求解的門限Λopt與統計量進行比較，一旦，則判定假設條件H0成立，此時剔除的矩陣行對應的位置可判定為信息比特位置，從而實現在該遍歷碼長下碼率及信息比特位置的識別，最后利用定理1 和定理2 的結論識別出真實極化碼碼長，同時獲得該碼長下的信息比特位置，具體如算法1 所示。

算法1極化碼參數識別算法

3.4 算法計算復雜度分析

不妨設截獲的數據量為L，遍歷的碼長范圍為。當遍歷的碼長為時，需要對2m個信息比特位置進行遍歷，而對每一個信息比特位置進行遍歷時，需要進行次元素大小比較、次向量加法運算及一次門限解算。由于克羅內克積矩陣構造是固定的，故在識別之前，可以將對偶向量求解并保存，從而減少計算量。為方便描述，本文把一次比較大小等價為一次向量加法運算，將以此門限計算等價于20 次向量乘法，故對碼長為2m進行遍歷時，需要20 × 2m次向量乘法和L2m次加法運算。對不同遍歷碼長下的計算量求和，得到總的乘法計算復雜度為加法復雜度為。由此可見，本文算法計算量近似與截獲的數據長度及遍歷的最大碼長成線性增加。

4 仿真分析

在本節仿真中，首先驗證本文算法對極化碼參數識別的有效性；其次，考察極化碼碼長、截獲碼字數目及碼率3 個因素對算法正確識別率的影響；最后，對比了在硬判決與軟判決2 種條件下算法的性能，以突出軟判決序列的優勢。

4.1 算法有效性驗證

首先，從圖3(a)和圖3(c)來看，當遍歷的極化碼碼長小于實際碼長128 時，碼長逐漸減小，碼率逐漸增加，直到增加到1；而當編碼的碼長大于128 時，碼長逐漸增加，而碼率保持不變，這與定理1 與定理2 的結果完全一致；其次，分析圖3(b)及圖3(d)可知，當剔除的位置為凍結比特位置時，對應的對偶向量與碼字能夠保持校驗關系，反之當剔除的是信息比特位置時，對偶向量與碼字之間的校驗關系不在成立，這說明定理3 的結論是一致的。通過設定的判決門限來檢測這種校驗關系，正好能識別出信息比特位置，從而完成極化碼生成矩陣的識別。雖然圖3(d)中碼字受到了噪聲的干擾，但是設定的門限仍然能夠有效地完成參數識別，這說明本文提出的算法對噪聲具有較強的穩健性。

圖3 低信噪比與高信噪比下，本文所提算法的有效性驗證

4.2 算法容錯性驗證

1) 碼長對算法性能的影響

仿真設定極化碼碼長分別為32、64、128、256、512 和1 024，每種極化碼的碼率為每一種極化碼下的碼字為2 000 個，設定信噪比范圍為?2～8 dB，間隔為0.25 dB，蒙特卡羅實驗次數為1 000，統計在不同信噪比下每種極化碼參數（包括碼長、信息比特位和凍結比特位）的識別率，結果如圖4所示。

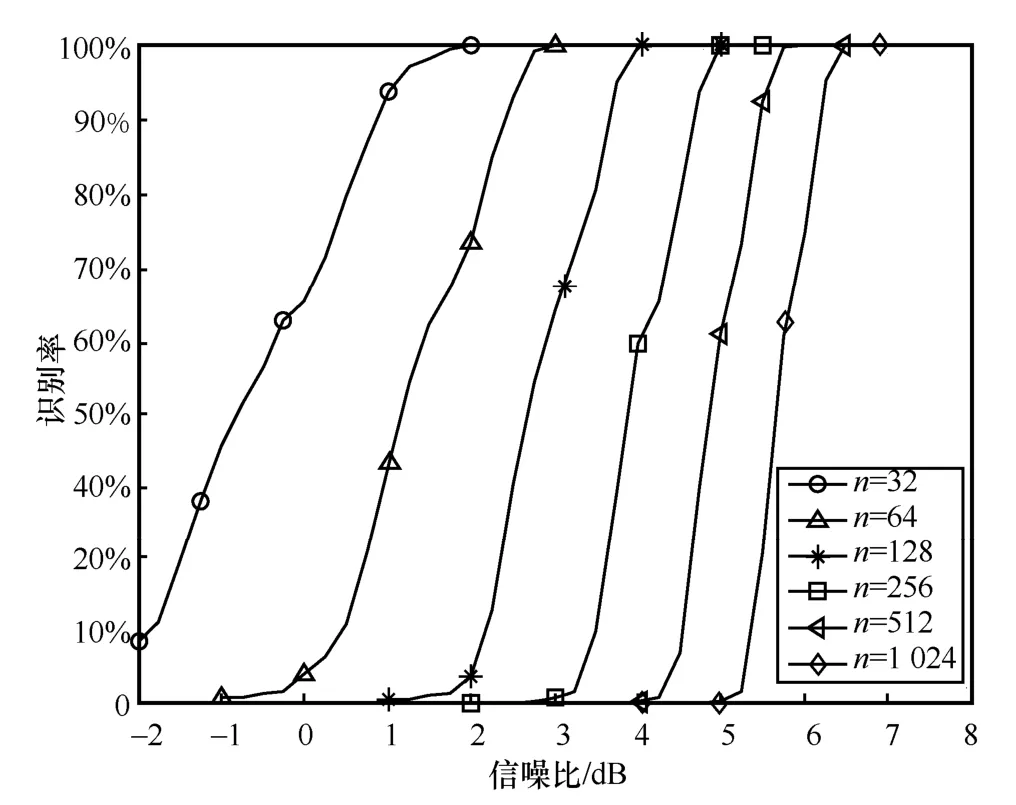
圖4 不同碼長對算法影響

從圖4 結果來看，本文所提算法的性能隨著碼長的增加，性能逐漸變差，主要原因在于，在同一碼率條件下，碼長越長，需要準確識別的極化碼的信息比特位置就越多，故在同等條件下，碼長越長，出現對信息比特位置的誤判概率就越大，故越難識別極化碼參數。此外，從識別率來看，本文所提算法在信噪比為6.5 dB 條件下，對碼長為1 024 的極化碼參數識別率達到98%以上，這說明了算法具有較好的低信噪比穩健性。

2) 碼字數目對算法影響

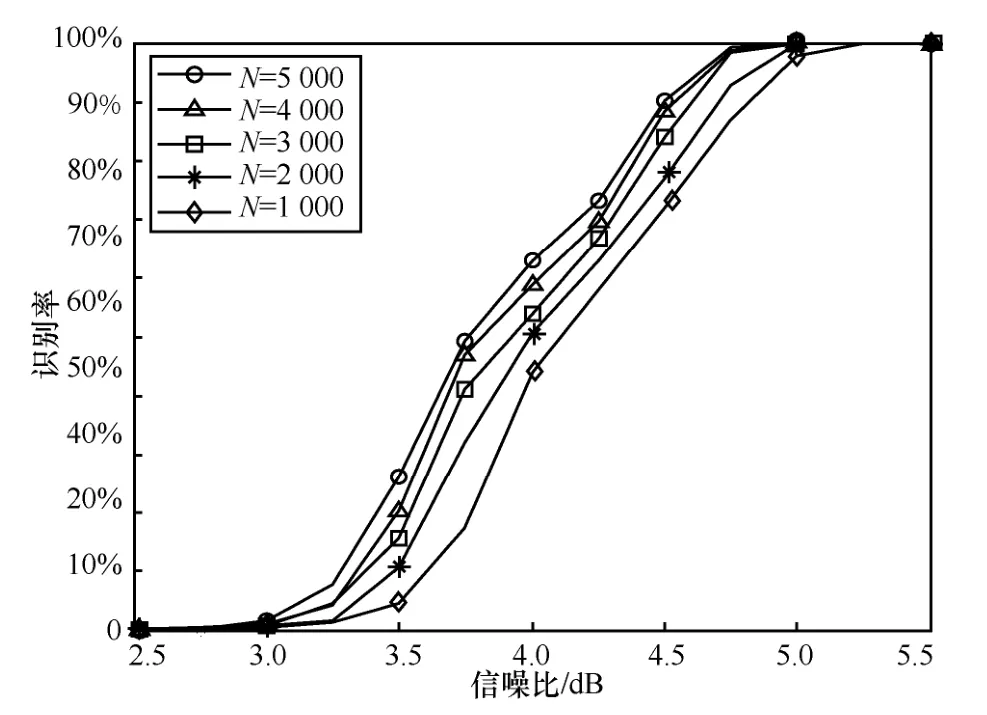
圖5 不同碼字數目對算法影響

從圖5 結果來看，通過增加極化碼碼字個數，可以有效地提高參數識別正確率。主要原因在于，碼字個數越大，求取的統計量就越近理論均值，此時對信息比特位置的誤判概率就會減少，從而算法識別性能就增加了。

3) 碼率對算法影響

仿真設定極化碼碼長為64 和128，每種碼長下的極化碼碼率分別為設定截獲的碼字個數為2 000 個，蒙特卡羅實驗次數為1 000 次，統計2 種碼長在不同碼率下極化碼參數的正確識別率，結果如圖6 所示。

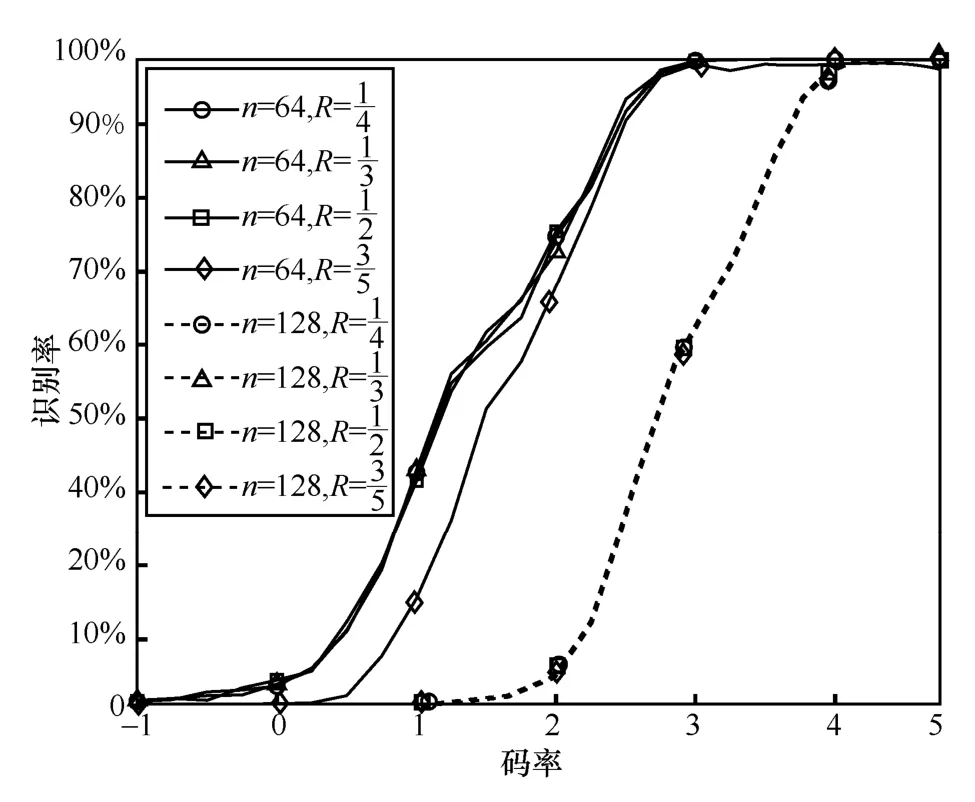
圖6 不同碼率對算法的影響

從圖6 結果來看，極化碼參數識別概率與碼率大小關系不大。主要原因在于，雖然碼率增加，會導致信息比特位置的增加，但是在識別過程中，每種碼率上的信息比特位置所對應的對偶向量碼重卻非常接近并且都比較小，即使碼率增加，信息比特位置的誤判率變化也不會太大，故在不同碼率下，極化碼識別非常接近。

4.3 與硬判決方法對比

為了突出采用軟判決序列的優勢，本節將采用了硬判決序列的算法進行對比。仿真設定極化碼碼長為64、128、256 及512，每種極化碼碼率為截獲的碼字個數為2 000，設定信噪比范圍為0～7 dB，間隔0.25 dB 取值，蒙特卡羅實驗次數為1 000，統計在2 種不同序列類型下，算法的識別性能，結果如圖7 所示。

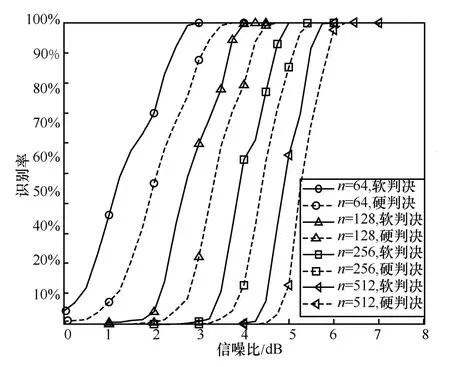
圖7 與硬判決算法對比

從圖7 結果來看，基于軟判決序列的識別方法性能要明顯好于基于硬判決的方法，軟判決算法的性能提升近0.5 dB。主要原因在于，與硬判決序列相比，軟判決序列包含豐富的信道噪聲信息，而本文所提算法能夠充分利用軟判決序列，故其在低信噪比下的穩健性會更強。

5 結束語

基于極化碼的編碼結構，首先給出并證明了定理1 和定理2，即原始極化碼具有最小的碼率，同時所有具有最小碼率的極化碼碼長中，原始極化碼的碼長最短；其次為了求解不同碼長下極化碼的碼率、信息比特位及凍結比特位，給出并證明了定理3；然后為了在低信噪比情況下實現極化碼信息比特位置參數識別，引入了LLR 概念，基于定理3 及LLR 的統計特性，設定出最優的信息比特位判決門限，從而在低信噪比下，快速識別出極化碼編碼參數。仿真結果驗證了本文所提算法的有效性和較強的低信噪比下的容錯性，在非合作通信領域具有較好的應用前景。