基于注意力機制的泊位占有率預測模型研究

王竹榮，薛偉，牛亞邦，崔穎安，孫欽東，黑新宏

（西安理工大學計算機科學與工程學院，陜西 西安 710048）

1 引言

近年來，智能交通系統（ITS,intelligent transportation system）迅速發展[1]。停車誘導信息系統（PGIS,parking guidance information system）是ITS 中不可缺少的組成部分，泊位占有率預測是其中一項重要技術。根據國際停車協會（IPI,International Parking Institute）的一項調查，超過30%的汽車在公路上尋找停車位，而這些巡航汽車在城市地區造成了高達40%的交通堵塞[2]。研究數據顯示，在公路的車流量中，泊車車輛占道路車流量的12%～15%。尋找車位的過程會增加30%的燃油消耗[3]。泊位占有率預測和泊位信息共享對停車場的日常運行、調度規劃以及交通運行狀態具有重要影響。泊位占有率預測已經引起學術界和工業界的廣泛關注。例如，谷歌地圖基于用戶調查和軌跡數據[4]預測全市范圍內的停車困難程度；百度地圖基于環境上下文特征（如興趣點、地圖查詢等），估計全市范圍內的實時停車位可用信息[5]。上述方法是對某一區域的停車難度進行預測和分級，這可能導致對于單個停車場的泊位占有率預測結果不準確。

現有的泊位占有率預測方法主要為基于統計學的預測方法和基于機器學習的預測方法。基于統計學的預測方法雖然計算較為簡單，時間復雜度較低，但是預測精度不高且穩定性較差。例如，Dunning 等[6]提出建立一個停車場數據收集以及泊位預測的PGIS，利用差分整合移動平均自回歸模型進行泊位占有率預測，實驗結果表明該模型的預測效果并不穩定，僅能預測占有率相對平穩的時間段，在出現波峰或者波谷的時間段預測效果較差。Caliskan 等[7]利用PGIS 采集的車輛抵達停車場的時間和停車場泊位占有率等歷史數據，使用連續時間齊次馬爾可夫與排隊論預測方法進行泊位占有率預測。Chen 等[8]對泊位占有率預測展開研究，結合泊位占有率的外在影響因素，利用通用代數建模系統（GAMS,the general algebraic modeling system）進行建模求解，泊位占有率預測精度有一定提升。Rajabioun等[9]和Klappenecker等[10]通過數學方法進行泊位占有率預測，該方法依賴于參數控制，具有很強的樣本依賴性，雖然降低了計算的時間復雜度，但穩健性較差。Richter 等[11]通過分析停車場的泊位歷史數據，對泊位數據時間和空間進行聚類，來選擇最優的時空特征，預測準確性進一步提高。為解決基于統計學泊位占有率預測方法的不足，基于機器學習的泊位占有率預測方法近幾年大量涌現。楊兆升等[12]將BP（back propagation）神經網絡應用到泊位占有率預測問題中。陳群等[13]利用相空間重構對泊位數據進行預處理，并利用Elman 神經網絡泊位預測方法進一步提升模型預測精度。Blythe 等[14]和季彥婕等[15]提出基于小波變換的泊位預測模型，然后利用啟發式算法對神經網絡進行優化，提出粒子群優化的小波神經網絡停車場泊位預測模型。陳海鵬等[16]采用小波變換和 ELM（wavelet transform with extreme learning）相結合的方法進行泊位的短時預測，所提模型在不降低預測精度的情況下，提升了傳統神經網絡的訓練效率。韓印等[17]提出基于灰色?小波神經網絡的有效泊位預測算法。

綜上分析可知，基于統計學的泊位預測方法在時間復雜度方面具有優勢，但是預測精度相對較低且樣本依賴性強。與之相比，基于機器學習的泊位預測方法的預測精度大幅提升，適合時間跨度較長的泊位預測場景要求。

泊位占有率預測是一種具有典型時間序列特征的時間序列預測問題。隨著深度學習在圖像處理和自然語言領域的發展，很多新的神經網絡模型和方法被用于時間序列預測問題，如Seq2seq 模型結合殘差網絡[18]、深度神經網絡結合統計學方法的ARMAM（autoregressive moving average model）[19]、基于注意力機制的長短時記憶網絡[20]、基于時間注意力學習的多視野時間序列預測方法[21]、基于時間模式的神經網絡[22-23]、基于DTW（dynamic time warping）的直覺模糊時間序列預測模型[24]和利用直覺模糊多維取式推理建立的高階模型[25]。其他的模型介紹如下。自注意力機制轉移網絡模型[26]通過矩陣控制序列權重的學習方式學習特征信息，主要適用于自然語言處理問題，是目前自然語言處理研究和應用最為廣泛的模型。自注意力機制的卷積模型[27]通過改變自注意力機制結構，將原有的注意力用于計算全局的隱含層向量權重，此模型利用卷積神經網絡（CNN,convolutional neural network）獲取局部信息，將時間復雜度從O(n2)降低到O(n(logn)2)，加快了運算速度。基于社會注意力的行人軌跡預測模型提高了預測的可解釋性和預測精度[28]。何堅等[29]提出了綜合考慮多維時空因果關系的泊位占有率預測技術和方法。梅振宇等[30]對泊位占有率序列的復雜性度量方法進行了分析。

從長遠發展角度考慮，PGIS 不僅要及時地為用戶提供的泊位信息，還應對未來一段時間的泊位需求信息做出預估，給予用戶更長時間進行出行規劃。因此，泊位的中長期預測研究是必要的。目前，對泊位占有率中長期預測的研究相對較少，現有的預測方法主要以傳統的迭代計算為主，預測效果較差。深度學習方法提供了處理多元時間序列的預測新思路。對泊位的中長期預測方法進行研究，在增加預測步長的前提下，提升預測精度及預測序列的穩定性指標成為必要工作。

本文主要工作如下。1)提出了一種高效的時間序列預測模型。所提模型以sequence-to-sequence 為整體框架，以雙向長短時記憶（BiLSTM,bi-directional long short-term memory）網絡[31]為模型的編碼器和解碼器的內部結構，通過一維CNN 提取多變量的局部特征作為模型的注意力機制，捕獲泊位預測問題特征的時間模式信息。2)將所提模型用于預測泊位占有率數據預測，測試結果及對比分析表明，所提帶有注意力機制的神經網絡模型有較強的非線性特征提取能力，與 LSTM（long short-term memory）網絡模型相比預測精度較高，有較強的穩健性和穩定性。

2 基于注意力機制的sequence-to-sequence泊位預測模型

sequence-to-sequence 模型實現了從一個序列到另一個序列的轉換。Google 曾用 sequence-tosequence 模型加注意力機制來實現翻譯功能。sequence-to-sequence 模型突破了傳統的循環神經網絡（RNN,recurrent neural network）模型輸入輸出序列大小固定的限制。sequence-to-sequence 由編碼器（encoder）和解碼器（decoder）兩部分組成，能有效提取輸入數據的特征。停車場泊位數據具有典型的時間序列特征，通過歷史數據預測未來停車場占有率，符合序列到序列模型的時間數據序列特征。因此，本文利用sequence-to-sequence模型結合時間模式的注意力機制進行泊位占有率預測。

本文采用sequence-to-sequence 編解碼器結構作為泊位預測模型，其中編碼器和解碼器采用BiLSTM 網絡。編碼器端將不定長序列輸出為定長序列，由于輸入序列較長，解碼器端難以獲得有效的數據信息。因此，本文引入注意力機制，增強局部數據特征學習能力，保留BiLSTM 編碼器對輸入序列的輸出，通過CNN 獲得多變量的時間模式信息，并存儲上下文信息。通過對模型進行訓練，根據學習特征信息，將輸入序列與模型輸出關聯起來，并對相關性高的序列分配較高的學習權重，用輸出序列提取高度相關的有用特征。解碼器將結合編碼器輸出信息及注意力機制存儲的時間模式信息，輸出預測目標序列。

2.1 BiLSTM 工作原理

BiLSTM 是雙向LSTM，由前向LSTM 與后向LSTM 組合而成，它們用來建模上下文信息，具有更強的長期信息記憶能力。

BiLSTM 的單元結構如圖 1 所示，其中(x1,x2,…,xm)為輸入序列，LSTML為前向LSTM，LSTMR為后向LSTM，hLm為前向LSTM 隱藏狀態向量，hRm為后向LSTM 隱藏狀態向量，ht為BiLSTM 的隱藏狀態向量。BiLSTM 的隱藏狀態需要結合前向和后向2 個方向的隱藏狀態。

BiLSTM 的隱藏狀態向量為

BiLSTM 是由2 條LSTM 鏈式結構組成，而LSTM 的內部結構可參見文獻[32-33]。

BiLSTM 中的單向LSTM 描述如下。每一個步長t與其對應的輸入序列為X={x1,x2,…,xw}（w為滑動窗口大小），網絡內部單元中包括輸入門it、遺忘門ft、輸出門ot和隱含層ht。狀態單元ct通過控制it、ft和ot來控制數據的記憶及遺忘，如式(2)～式(9)所示。

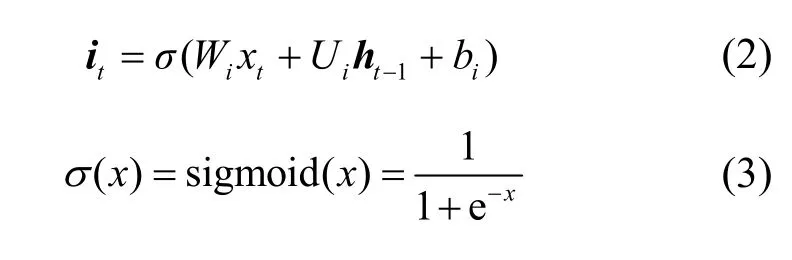
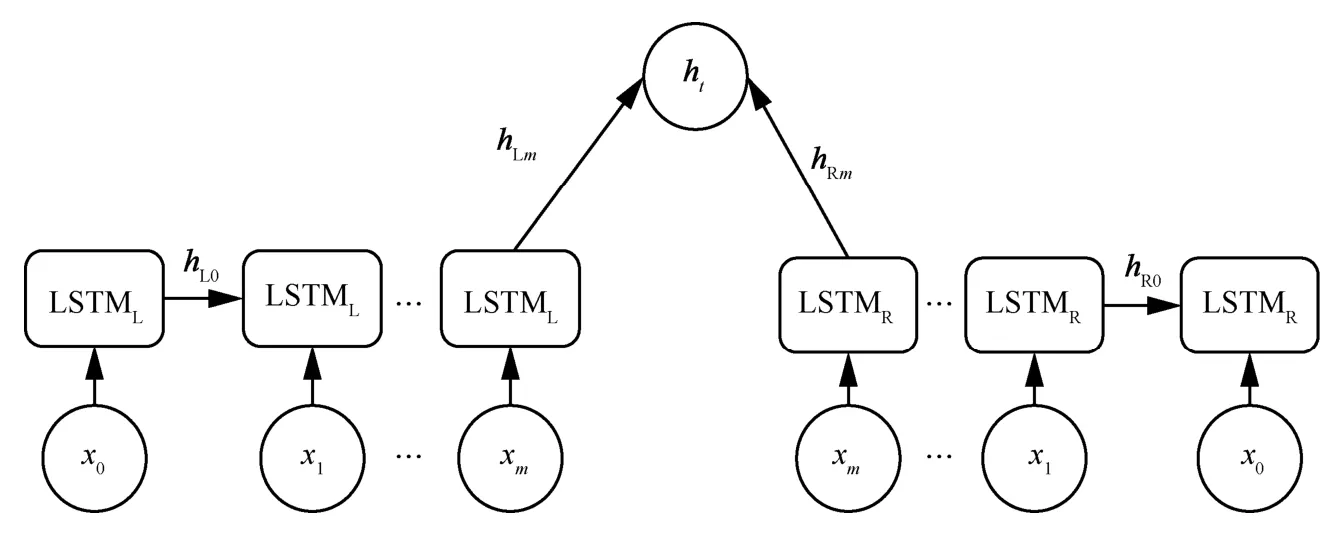
圖1 BiLSTM 單元結構

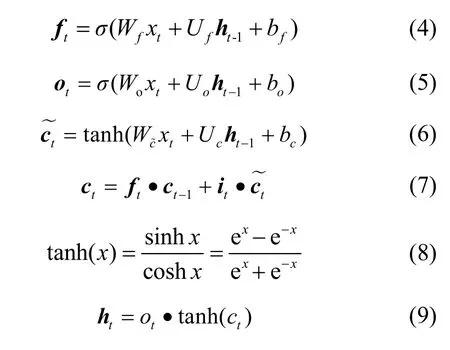
其中，Wi、Wf、Wo、表示輸入過程的權重參數，Ui、Uf、Uo、Uc表示狀態轉移權重參數，b i、bf、bo、bc表示偏差參數，表示候選記憶細胞，tanh(?)表示雙曲正切函數，·表示點乘。

sigmoid 函數σ(x)為一個logistic 函數，它可以將一個實數映射到(0,1)。tanh(?)是雙曲正切函數，它可以將數值縮放到(?1,1)。三類門限控制單元共同控制信息進入和離開記憶細胞，輸入門it調節進入記憶細胞的新信息，遺忘門ft控制記憶細胞中保存的信息，輸出門ot定義輸出信息。LSTM 的門結構使時間序列上的信息形成一個有效的依賴關系。

2.2 sequence-to-sequence 模型結構

sequence-to-sequence 模型在處理序列任務時，對輸入序列或輸出序列的長度沒有限制，可執行不定長輸入和不定長輸出。sequence-to-sequence 模型結構如圖2 所示。

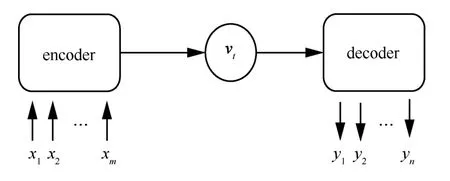
圖2 sequence-to-sequence 模型結構

圖2 中，sequence-to-sequence 模型由編碼器、上下文向量vt和解碼器組成。編解碼器通常是多層的RNN 或LSTM 結構，本文選擇BiLSTM 網絡作為編碼器和解碼器網絡。上下文向量vt包含了x1,x2,…,xm隱含層編碼信息。對于時間t，將編碼器隱含層ht、解碼器之前時刻的輸出yt?1、之前時刻的隱含層狀態st?1以及vt輸入解碼器。最后得到解碼器的隱含層狀態st，解碼器對輸出值進行預測。

sequence-to-sequence 編解碼器結構模型計算式如式(10)和式(11)所示。

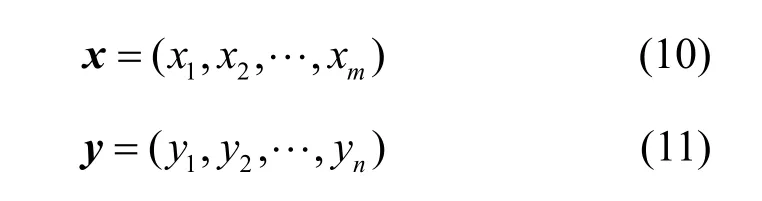
其中，x和y分別為sequence-to-sequence 編碼器端輸入序列和解碼器端最終輸出預測值。

編碼器輸入端是x和上一個時間步的隱藏狀態ht?1，輸出端是當前時間步的隱藏狀態ht，即

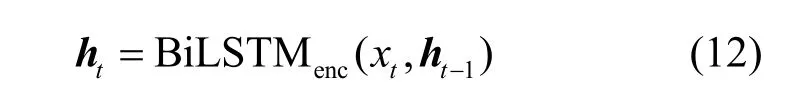
對原始時間序列使用BiLSTMBlockCell 處理，得到每個時間步的隱藏狀態hi（hi為列向量），每個hi維度為m，w是滑動窗口長度，得到的隱藏狀態矩陣。隱藏狀態矩陣的行列向量意義如下。

1) 行向量代表單個變量在所有時間步的狀態，即同一變量的所有時間步構成的向量。

2) 列向量代表單個時間步狀態，即同一時間步下的所有變量構成的向量。

2.3 TPA 機制

所提模型中利用一維CNN 學習時間序列數據的時間模式信息，即TPA（temporal pattern attention）作為網絡的局部特征學習方式[23]。TPA 機制結構如圖3 所示。圖3 中最左側箭頭表示對變量的處理，每一行表示一個變量的時間序列數據。通過卷積計算獲得該變量在卷積核范圍內的時間模式矩陣，評分函數計算時間模式矩陣的分值，并通過sigmoid 函數將分值歸一化，獲得注意力權重α，結合時間模式矩陣及注意力權重計算得到上下文向量vt。將encoder 中的上下文向量vt及隱藏狀態ht，與decoder 中的隱藏狀態st進行連接，并通過輸出層及softmax 函數來計算輸出預測值。

以下詳細描述TPA 機制在所提模型中的作用機理。

首先，利用一維CNN 進行卷積計算。

卷積配置為k個濾波器（filter），卷積核（kernel）尺寸為1×T（T代表注意力所覆蓋的范圍，通常令T=w），將上述kernel 沿隱藏狀態矩陣H的行向量計算卷積，提取該變量在該卷積核范圍attn_length內的時間模式矩陣如式(13)所示。

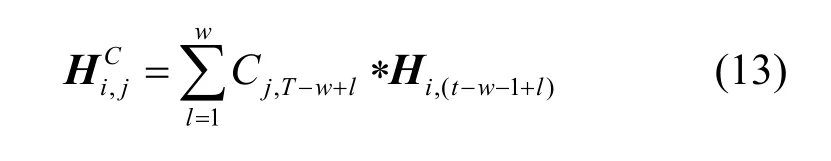
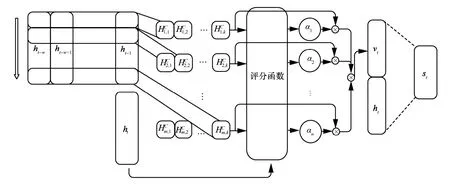
圖3 TPA 機制結構

對上述學習到的時間模式進行評分，時間模式的評分函數f為

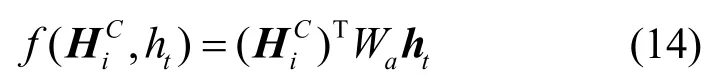
注意力權重αi為

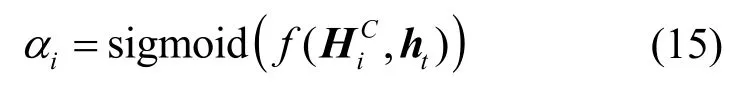
對HC的每一行做加權求和，得到上下文向量vt為

其中，αi為時間模式矩陣HC的第i行注意力權重，為時間模式矩陣HC的第i行。

將上下文向量vt與encoder 的隱藏狀態ht傳入decoder。將encoder 的隱藏狀態ht、上下文向量vt與decoder 隱藏狀態st連接，如式(17)所示。

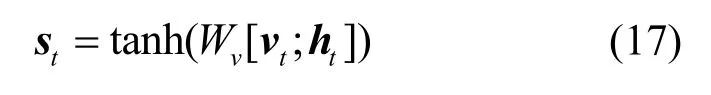
其中，Wv為權值參數。

decoder 通過接收前一個輸出序列yt?1以及decoder 的上一個時間步的隱藏狀態st?1和上下文向量vt計算當前隱藏狀態st，如式(18)所示。

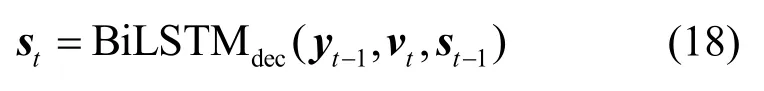
最后，結合decoder 當前時間步隱藏狀態st及上下文向量vt，通過輸出層及softmax 函數來計算輸出yt，如式(19)所示。

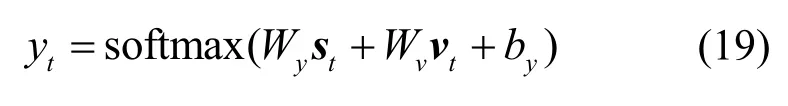
softmax 函數是一個概率函數，max 表示取大概率最大值，它的作用是將所有輸出映射到(0,1)，softmax 最大值作為最終的輸出。

假設有一個數組Y，數組長度為k，yi表示Y中的第i個元素，那么元素yi的softmax 值為

2.4 基于注意力機制的sequence-to-sequence 泊位占有率預測算法

泊位占有率預測過程如圖4 所示。首先，獲取目標停車場歷史停車數據信息；然后，對數據進行清洗及預處理，對基于注意力機制的sequence-to-sequence泊位預測模型進行訓練；最后，將訓練好的預測模型進行泊位預測。基于注意力機制的sequence-to-sequence 泊位占有率預測算法流程如圖5 所示。

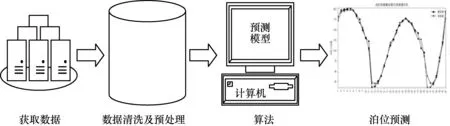
圖4 泊位占有率預測過程

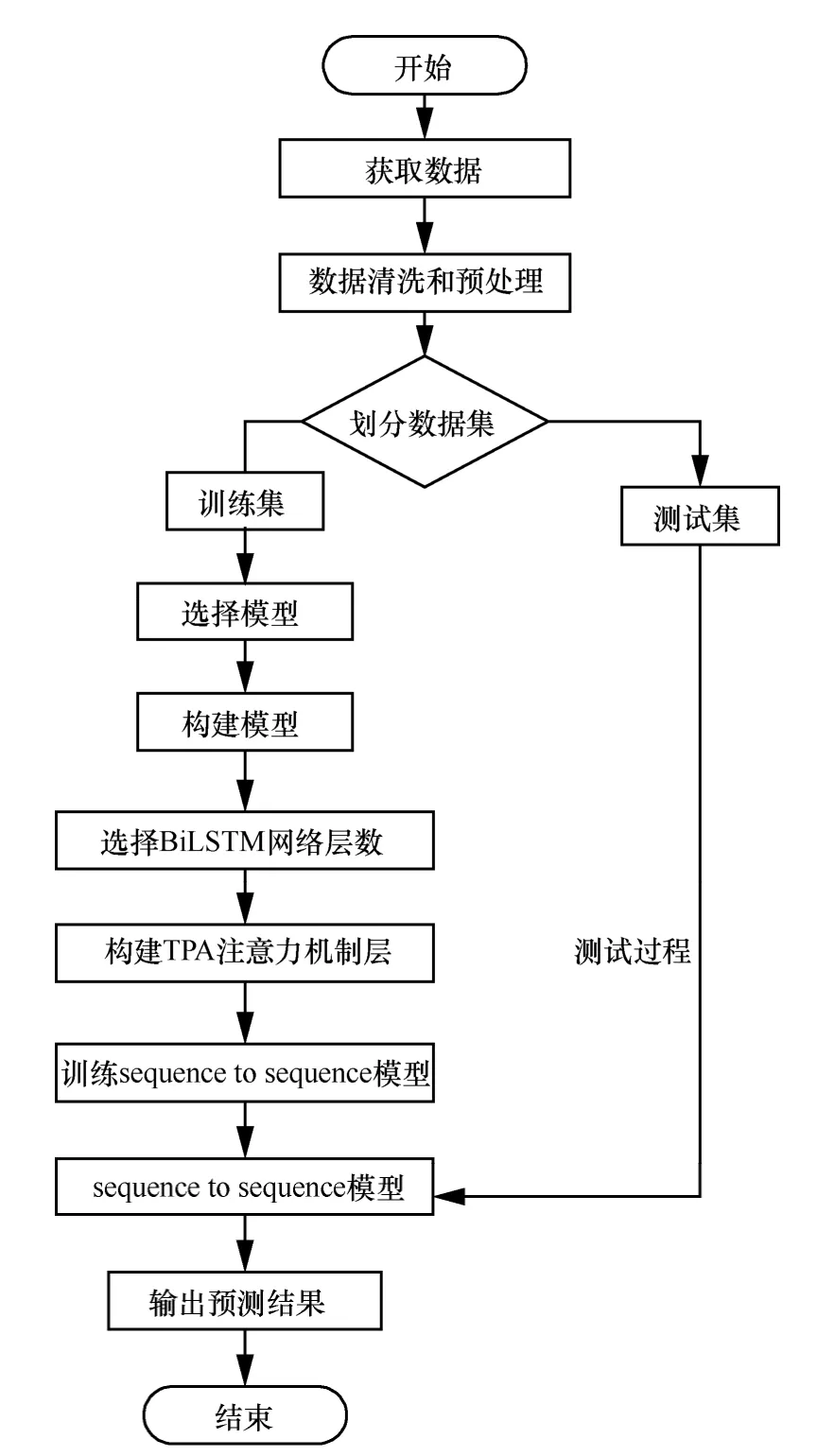
圖5 基于注意力機制的sequence-to-sequence 泊位占有率預測算法流程

基于注意力機制的sequence-to-sequence 泊位占有率預測算法如算法1 所示。

算法1基于注意力機制的sequence-to-sequence泊位占有率預測算法

1) 輸入原始數據；

2) 對數據進行清洗及預處理，包括缺失數據填充、剔除無用數據、數據標準化和歸一化；

3) 進行特征相關性計算和檢驗；

4) 劃分訓練集和測試集；

5) 建立基于sequence-to-sequence 泊位預測模型結構；

6) 構建TPA 機制層；

7) 用訓練集訓練基于注意力機制的sequence-to-sequence 泊位預測模型及結構參數，得到訓練好的預測模型；

8) 通過將測試集輸入訓練好的預測模型得到預測結果。

2.5 時間序列預測的評價指標

本文采用均方根誤差（RMSE,root mean squared error）和平均絕對誤差（MAE,mean absolute error）對所建模型的預測結果進行度量。RMSE 和MAE 計算式如式(21)和式(22)所示。

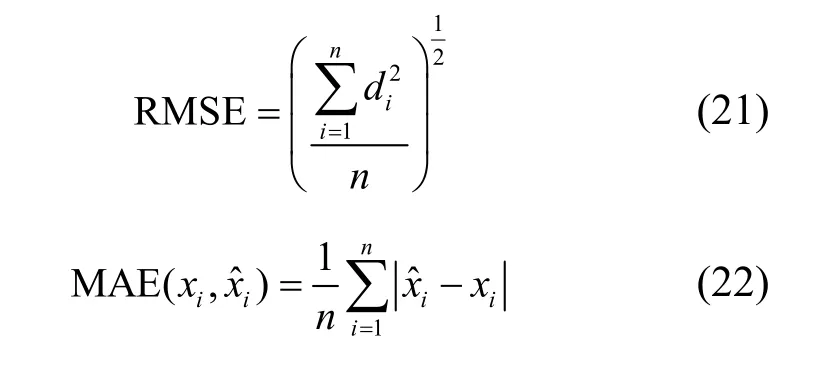
其中，n表示樣本數，di表示一組測量值與真實值的偏差，xi表示真實值，表示預測值。

MAE 范圍為[0,+∞)，當預測值與真實值完全吻合時MAE=0，為完美模型，誤差越大，MAE 越大。RMSE 描述所有預測結果的偏離程度，而MAE 在對預測結果進行評價時，可克服誤差相互抵消的問題，因此對于實際預測誤差大小的反映更為準確。

3 實驗分析

3.1 測試數據集

本文測試數據來自加州大學歐文分校（UCI,University of California Irvine）的停車場數據庫UCI，該數據集包括伯明翰市某區域內29 個停車場從2016 年10 月4 號至2016 年12 月19 號之間的36 285 條數據。數據信息包含停車場ID、停車時間、停車場的泊位數、已有車輛。本文使用數據集中包括BHMBCCMKT01 在內的28 個停車場的停車數據作為實驗測試數據。

所提模型選取泊位入駐數、天氣、節假日、工作日作為模型的4 個特征。首先對數據集中數據缺失值進行臨近均值填充，然后對數據集進行歸一化處理。對每個單個停車場數據集進行劃分，其中80%為訓練集，20%為測試集。

本文測試分為兩部分，第一部分測試所提模型的結構，并通過消融實驗，重點測試所提模型帶有注意力機制和不帶注意力機制的數據及對比分析；第二部分測試所提模型對停車場數據的測試結果及對比分析。

3.2 所提模型結構確定

本文采用sequence-to-sequence 編解碼器結構來預測泊位占有率，采用BiLSTM 結構進行編解碼操作，然后通過BiLSTM 層數優化模型參數。最初實驗的學習率設置為0.01，衰減率設置為0.5，隱含層節點的數量設置為64，CNN 設置4 個濾波器，卷積核大小為1 × 18。將數據集輸入網絡進行訓練，測試編碼器和解碼器不同層數BiLSTM 網絡的RMSE 變化情況。

本文分別對單層、雙層、三層、四層及五層BiLSTM 進行測試，并記錄各自的RMSE 變化過程。測試結果表明，當模型經過多次迭代RMSE 趨于穩定時，采用單層、四層BiLSTM 結構的訓練RMSE較大，經過雙層、三層及五層BiLSTM 結構訓練RMSE 相對較小且三層為最小。因此，本文選擇編碼器解碼器內部BiLSTM層數為RMSE最小的三層BiLSTM。在深度學習中，模型通過訓練從數據樣本中學習所有樣本的變化規律，容易導致過擬合或欠擬合。通過增加模型訓練迭代的次數，可以克服模型擬合不足的現象。對于過擬合的處理，對神經單元以一定概率斷開dropout，dropout 通過概率斷開神經網絡之間的連接，減少每次訓練時實際參與計算的模型的參數量，從而減少了模型的實際容量，來防止過擬合。需要注意的是，在測試時，dropout 會恢復所有的連接，保證模型測試時具有更強的泛化特性，使預測結果具有更好的多樣性。本文中dropout 概率設置為0.5。

3.3 泊位占有率模型確定與數據預測

以下實驗將利用所提模型分別對單個停車場BHMBCCMKT01和總體28個停車場的泊位占有率進行仿真測試。

3.3.1單個停車場數據測試分析及對比實驗

本節首先進行所提預測模型有注意力機制和無注意力機制在不同步長下對單個停車場數據執行預測的誤差對比分析，然后給出不同預測模型對單個停車場數據的預測精度的對比。

當訓練sequence-to-sequence 模型時，使用迭代預測，并且通過選擇模型的參數來獲得實驗結果。sequence-to-sequence 泊位預測模型參數如表1 所示，輸出步長為36，編碼器端BiLSTM 隱含神經元的個數E_hidden 和解碼器端BiLSTM 隱含神經元個數D_hidden 均為64，學習率Learning_rate 為0.001，遺忘率 Drop_rate 為 0.75，輸入特征數Input_dim 為4，迭代次數Epoch 為1 000，輸入數據長度Time_step 為18。

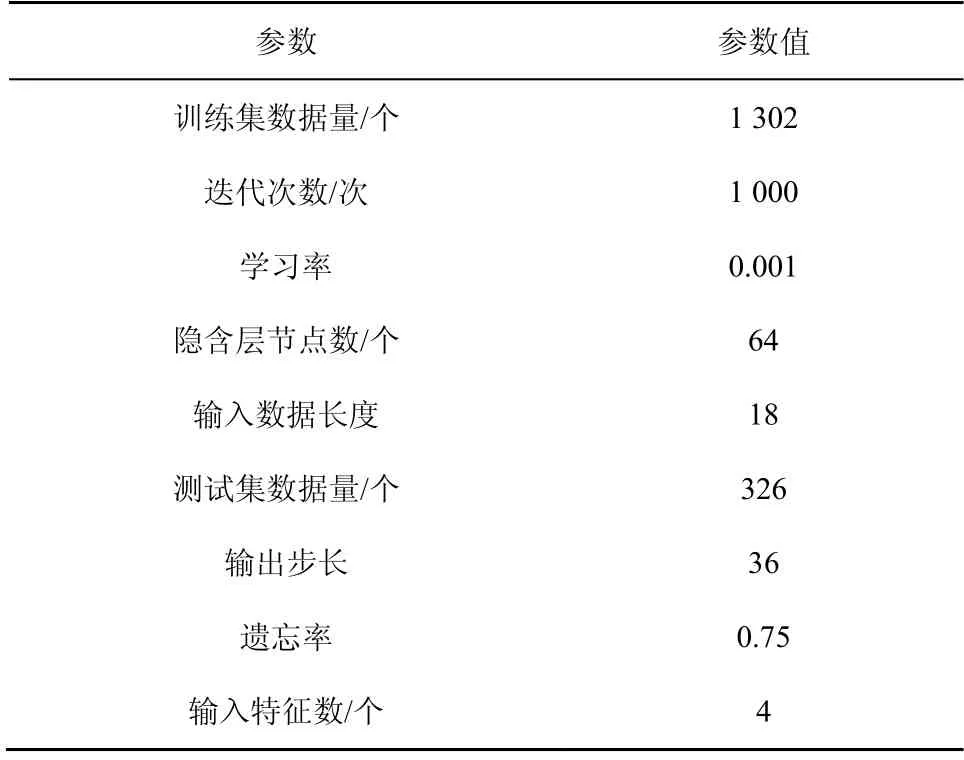
表1 sequence-to-sequence 泊位預測模型參數

表2 為所提模型有注意力機制和無注意力機制對數據集BHMBCCMKT01 的預測值與真實值對比，圖6 和圖7 為相應預測值與真實值對比曲線。圖8 為所提模型有注意力機制和無注意力機制下泊位預測MAE 隨步長變化的曲線。

由表2 數據可知，有注意力機制的預測數據平均誤差為6.75，無注意力機制的預測數據平均誤差為17.75。對比圖6 和圖7 可以看出，注意力機制在所提模型中具有重要作用。從圖8 可以看出，所提模型無注意力機制時，其MAE 隨步長的增加上升較快；而有注意力機制時，其MAE 隨步長的增加上升較慢。

當利用所提預測模型預測未來36 個目標步長的停車場泊位占有率時，其對應的真實值為194，而預測值為178，其誤差為16，預測結果可以滿足實際預測精度要求。綜上分析可知，所提模型在步長取較大值時預測結果的誤差相對穩定，模型可達到較好的預測效果。

3.3.2多個停車場數據測試分析

使用28 個停車場作為實驗數據，并對每一個停車場數據集按4:1 進行數據劃分，然后進行模型訓練和測試。使用基于注意力機制的sequence-tosequence 預測模型同LSTM 預測模型進行對比分析。表3為泊位占有率預測最小MAE，顯示了sequenceto-sequence 泊位占有率預測模型以及LSTM 泊位預測模型在數據集上的總體效果。LSTM 預測模型的預測步長為10，sequence-to-sequence 預測步長為36，從表3 中可以看出，sequence-to-sequence 泊位預測模型在28 個停車場的數據集測試中，有23 個預測結果的MAE小于或等于LSTM泊位預測模型。sequence-to-sequence 泊位預測模型MAE 的中位數（median）為0.021，LSTM 泊位預測模型MAE 的中位數為0.025。sequence-to-sequence 泊位預測模型MAE 的平均值（mean）為0.024，LSTM 泊位預測模型MAE 的平均值（mean）為0.028。sequenceto-sequence 泊位預測模型MAE 的最大值（max）為0.059，LSTM 預測模型MAE 的最大值（max）為0.078。sequence-to-sequence 預測模型MAE 最小值（min）為0.010，LSTM 泊位預測模型最小值（min）為0.008 6。從整體來看，sequence-to-sequence 泊位預測模型預測結果MAE 的中位數、平均值、最大值均優于LSTM 泊位預測模型。

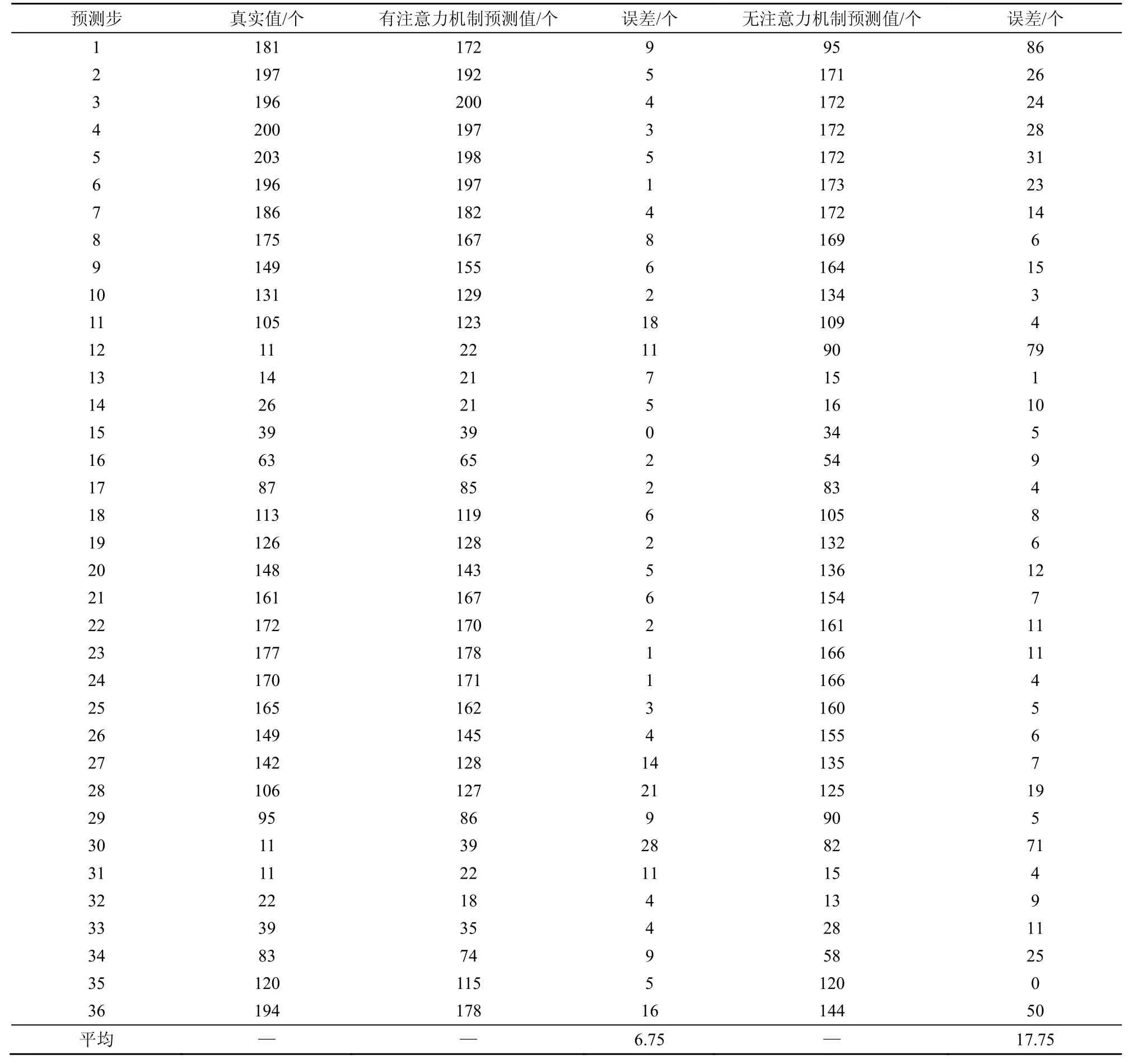
表2 所提模型有注意力機制與無注意力機制的預測值與真實值對比（步長=36）

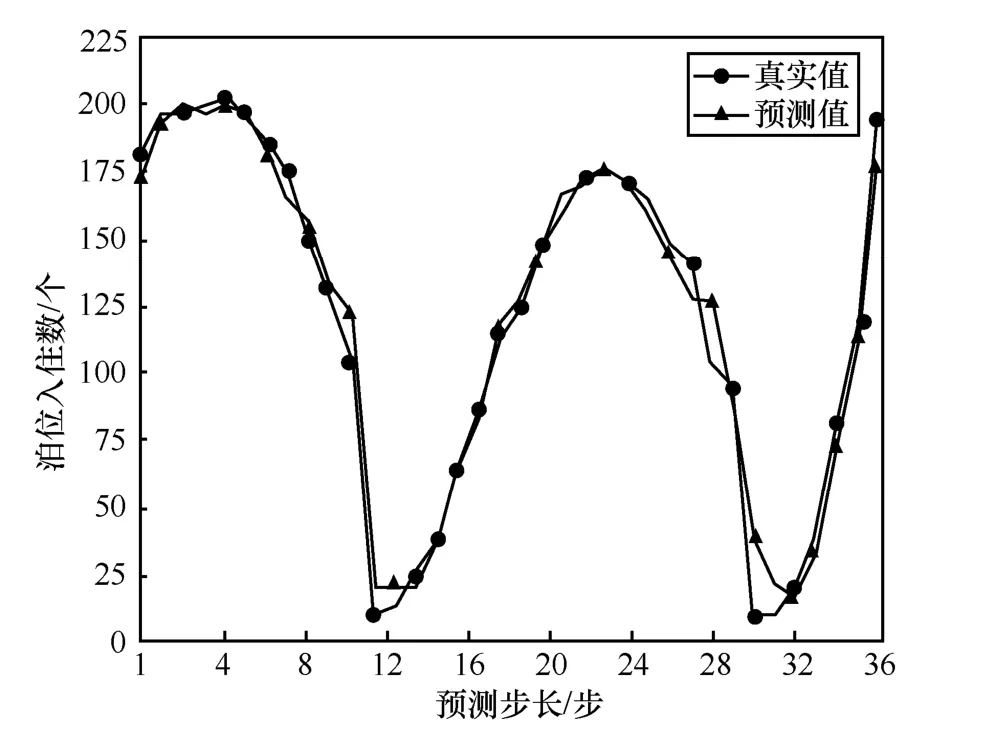
圖6 sequence-to-sequence 有注意力機制模型預測值與真實值對比曲線

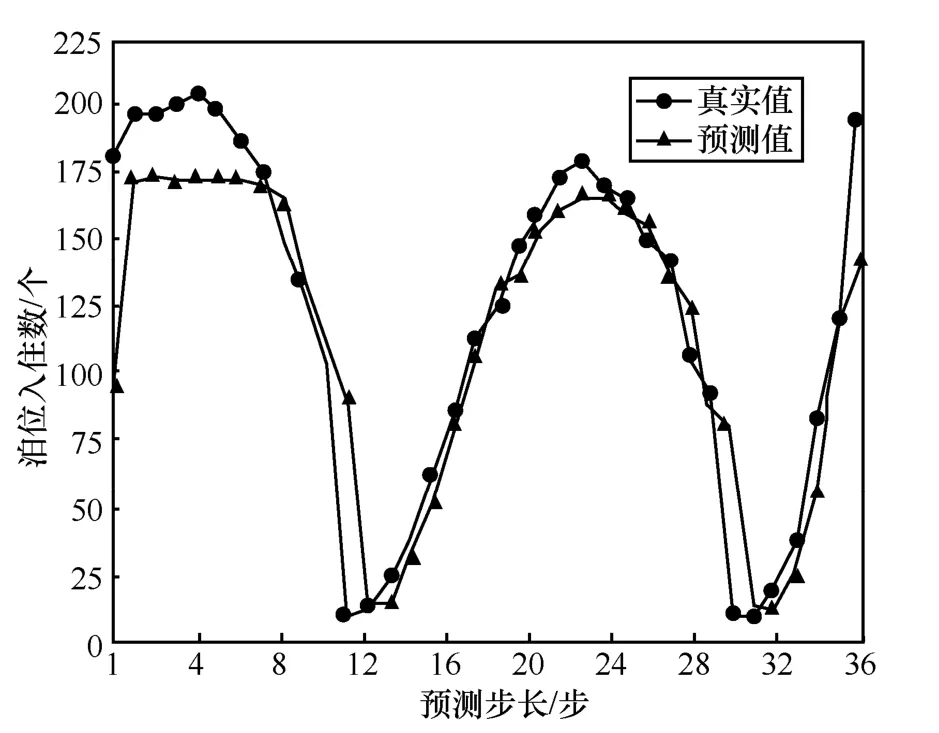
圖7 sequence-to-sequence 無注意力機制模型預測值與真實值對比曲線

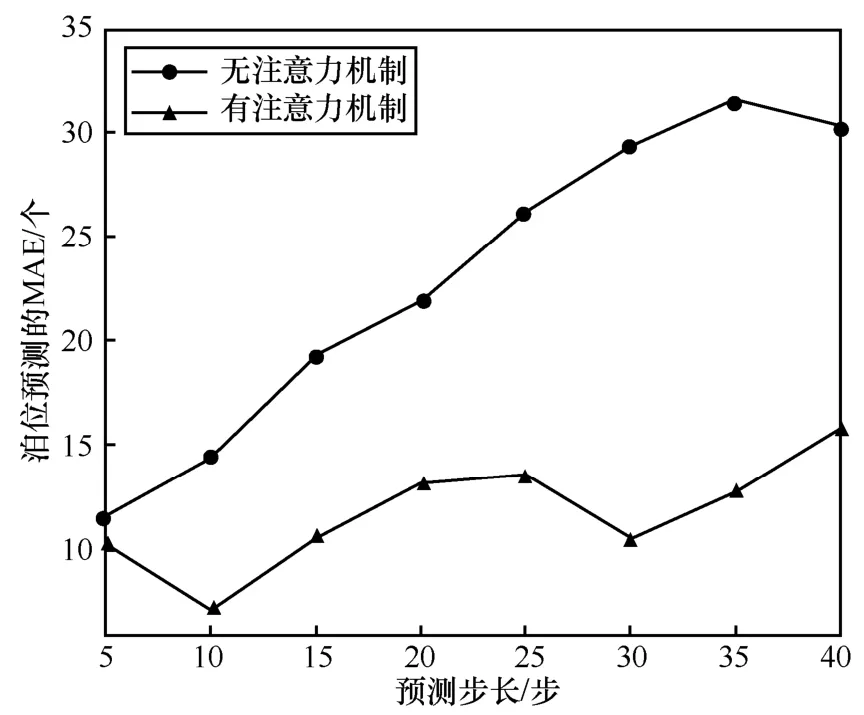
圖8 所提模型有注意力機制和無注意力機制MAE 隨步長變化的曲線

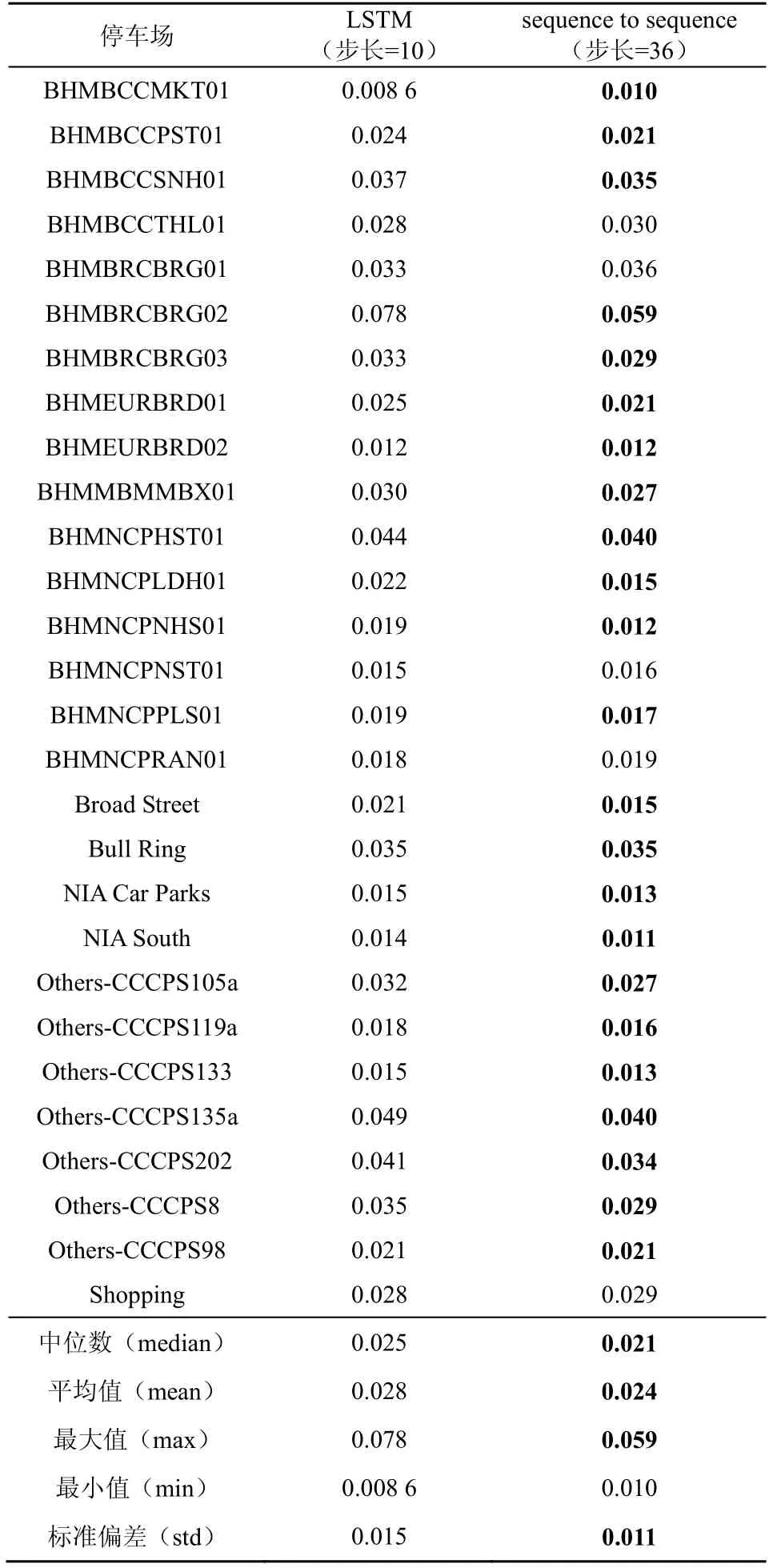
表3 泊位占有率預測的最小MAE 對比數據

如圖9 所示，sequence-to-sequence 泊位預測模型預測結果的MAE 更為集中且相對更小。因此，sequence-to-sequence 泊位預測模型預測精度整體優于LSTM 泊位預測模型且更為穩定。

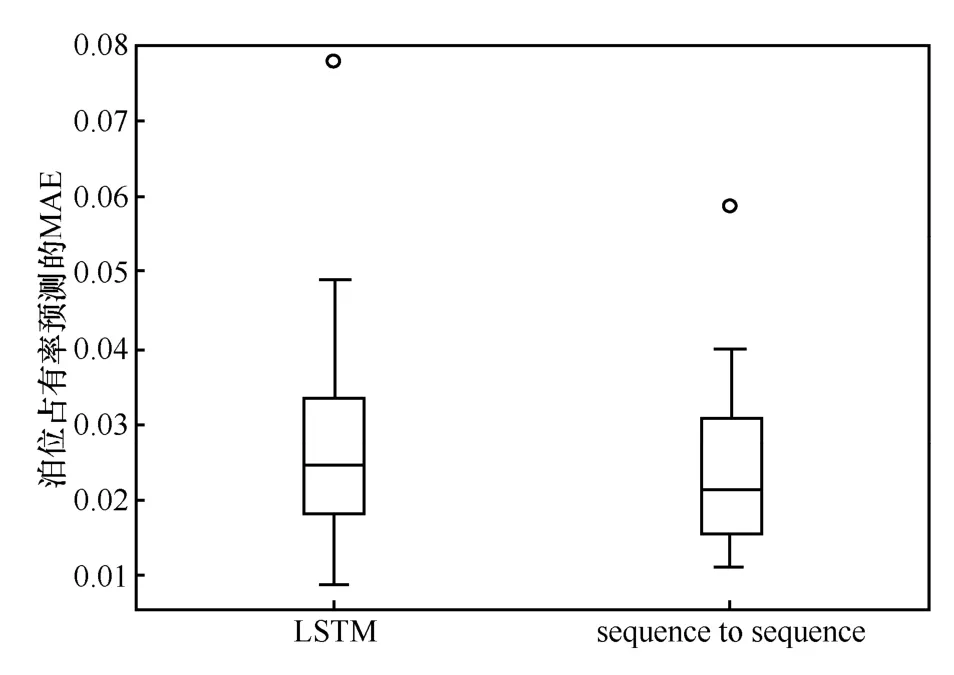
圖9 sequence to sequence 模型與LSTM 模型MAE 箱線圖分布

綜上所述，基于注意力機制的sequence-tosequence 泊位預測模型在泊位預測中，在增加了預測步長的前提下預測精度和穩定性均有提升。

4 結束語

本文以泊位占有率的預測作為研究對象，提出了一種基于注意力機制的sequence-to-sequence 模型對泊位占有率問題進行求解，為了提高泊位占有率的預測精度，在模型中將天氣、工作日、節假日等特征作為泊位占有率的融合特征，使模型的泛化能力更強，精度更高。在本文的預測模型中，利用時間模式注意力機制捕獲數據的局部特征，利用sequence-to-sequence 模型多輸入多輸出的特性，使模型的擬合能力更強。通過對模型的訓練和參數調整，對測試集進行測試，使用RMSE 和MAE 對模型預測結果進行評估，結果表明，所提模型表現出更好的預測效果。將所提模型與LSTM 模型的泊位占有率預測算法得到的預測數據進行比較，驗證了所提模型和方法的有效性。在未來工作中，將對存在奇異點和噪聲數據集的處理進行研究，并考慮泊位占有率的空間特征關聯信息，設計處理更為復雜情形的預測模型，致力于模型的理論分析和可解釋性，進一步提高預測精度，并推廣預測模型的應用前景。