小波神經網絡模型在滁河流域南京段洪水預報中的應用

朱永軍，湛忠宇

(江蘇省水文水資源勘測局南京分局，江蘇 南京 210008)

小流域洪水預報是當前水文科學中亟待研究的一個方向[1]。中國小流域眾多，洪水頻發，一般具有歷時短、突發性強等特點，洪水預報難度較大。特別是在梅雨季節，它經常會引發一系列地質災害，例如泥石流和滑坡，也很可能破壞生態環境等。因此，研究如何提高小流域洪水預報的精度十分有意義。

國內外學者紛紛對小流域洪水預報進行分析探討，基于物理意義的水文模型如新安江模型、SWAT模型、HEC-HMS模型等已廣泛應用于各個小流域[2-5]，并取得了顯著的成效。無需考慮物理過程的神經網絡可搭建輸入與輸出的復雜關系，引起了水文預報研究者的極大關注。1986年Rumelhart等正式提出BP神經網絡，1981年Jean Morlet建立了Morlet小波，1997年，李建平出版的《小波分析與信號處理——理論》，介紹并檢驗了小波分析的應用研究成果[6]，日益成熟的神經網絡應用于各個領域[7-8]，獲得了不錯的效果。BP神經網絡作為最常用的人工神經網絡[9]，已在河道洪水預報、降水徑流過程模擬中取得廣泛的應用[10-11]。BP神經網絡在收斂速度和適應性等方面仍有一定的提升空間，而小波神經網絡有更強的適應性和泛化能力，往往預報精度更高，在水文水資源等領域得到了很好的發展[12-15]。滁河流域南京段承受上游過境洪水的同時又受下游江潮頂托，洪水聚集較快而河道排泄不通[16]，洪水預報精度偏低，本文通過新建小波神經網絡和BP神經網絡洪水預報模型，應用于滁河流域南京段研究區，以此來對比模型的適應性和預報的準確性，從而為研究區選擇高效精準的洪水預報模型提供參考依據。

1 研究區概況

本文研究區滁河流域南京段位于江蘇省南京市六合區，屬于長江流域，區域面積約850 km2(圖1)。區域內河線迂回曲折，河床狹窄，主要支流包括皂河和八百河等。研究區降雨時空分布不均，大泉水庫站、馬集站、六合站、金牛山水庫站等記錄了降雨數據，出口處紅山窯閘站記錄了流量數據。圖1顯示了研究區域及其河流系統和測站的分布情況。

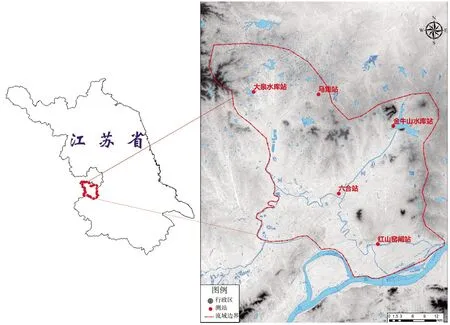
圖1 滁河流域南京段水系和測站分布

2 研究方法

小波神經網絡(wavelet neural network，即WNN)既體現了小波分析理論，又融入了神經網絡理論[6]。它的特點是以BP神經網絡結構為模板，在信號正向傳遞和誤差反向傳遞的循環過程中達到許可誤差。小波神經網絡三層之間各小波元互相關聯，而每層各自小波元之間無關聯。圖2是小波神經網絡結構示意。

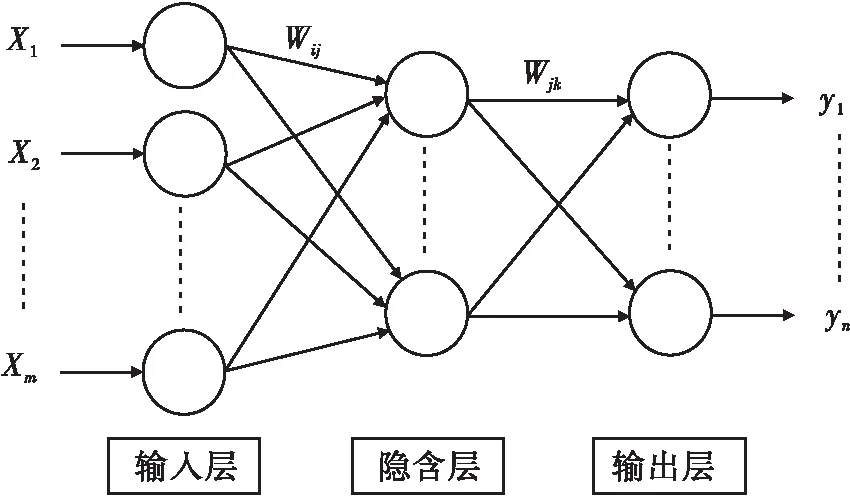
圖2 小波神經網絡結構示意

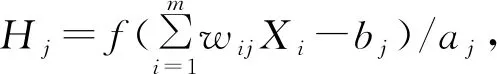
3 計算與分析

本文通過建立BP神經網絡洪水預報模型和小波神經網絡洪水預報模型，經過對比分析為滁河流域南京段提供高效精準的洪水預報模型。

3.1 選定樣本數據

樣本數據由輸入數據與輸出數據兩部分組成。但在實踐中小流域地區通常缺乏監控數據，例如暴雨、下墊面、溫度、蒸發等，這些都是可能影響洪水形成的重要因素。本文在研究區域內獲得了4個測站(大泉水庫、馬集、六合、金牛山水庫)的2010—2019年長系列降雨資料，依據泰森多邊形方法對4個站點雨量進行加權平均，得到小流域的面平均降雨系列，從中選定16場暴雨數據作為輸入數據。本文同樣獲得了流域出口處紅山窯閘站的2010—2018年長系列閘上水位數據，通過水位流量關系得到長系列流量數據，從中選定16場對應時刻的洪水數據作為輸出數據。

本文共選取了16組樣本(表1)，每組樣本包括80個數值為輸入數據、80個數值為輸出數據，樣本時段數為1 h。

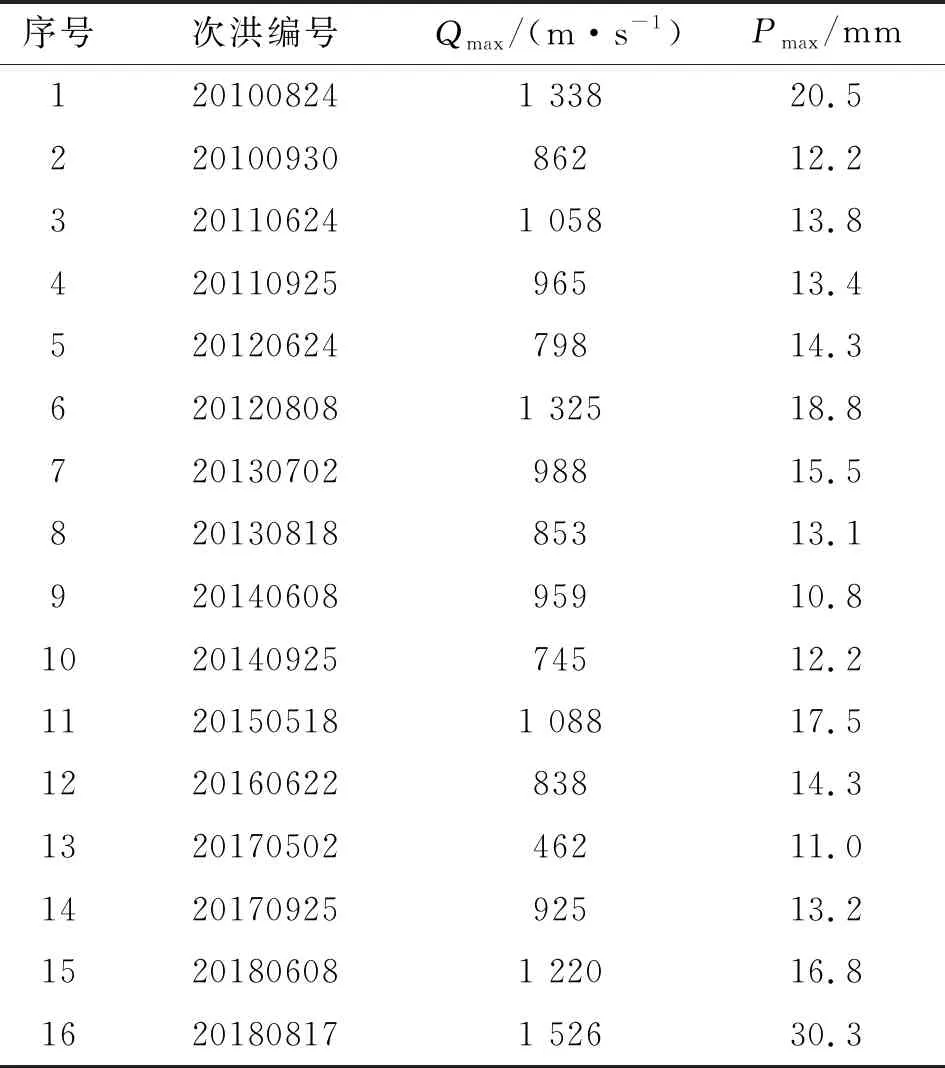
表1 場次洪水基本信息

為了加快模型收斂速度、提高模型精度，在網絡訓練之前通過式(1)對樣本數據進行歸一化，利于模型訓練的穩定性[7]。歸一化可將表達式去掉量綱，從而使樣本數據轉換到0～1范圍之內，變成純量。

(1)

3.2 參數初始化

參數包括兩部分，分別為小波神經網絡參數和BP神經網絡參數。小波神經網絡的參數有伸縮因子a、平移因子b和權值wij、wjk，BP神經網絡的參數有閾值和權值，這些參數都進行隨機初始化。小波神經網絡的隱含層激勵函數為小波函數，而BP神經網絡的可選用sigmoid函數。其余參數可設置一致，最大訓練次數為1 000，目標誤差為0.000 1，學習速率為0.01～0.50。

3.3 構建網絡結構

本文隨機選取8組樣本數據進行網絡訓練，4組進行網絡驗證，4組進行網絡測試。根據樣本數據，顯而易見輸入層和輸出層均有80個節點，而隱含層節點數可根據經驗公式(2)、(3)，從小到大依次試湊。在MATLAB中運行代碼，經過8組樣本數據訓練，模型自動對網絡的參數進行優化調整，再經過4組樣本數據驗證，最終確定小波神經網絡模型采用三層網絡結構80-22-80，BP神經網絡模型結構為80-36-80。

l

(2)

(3)

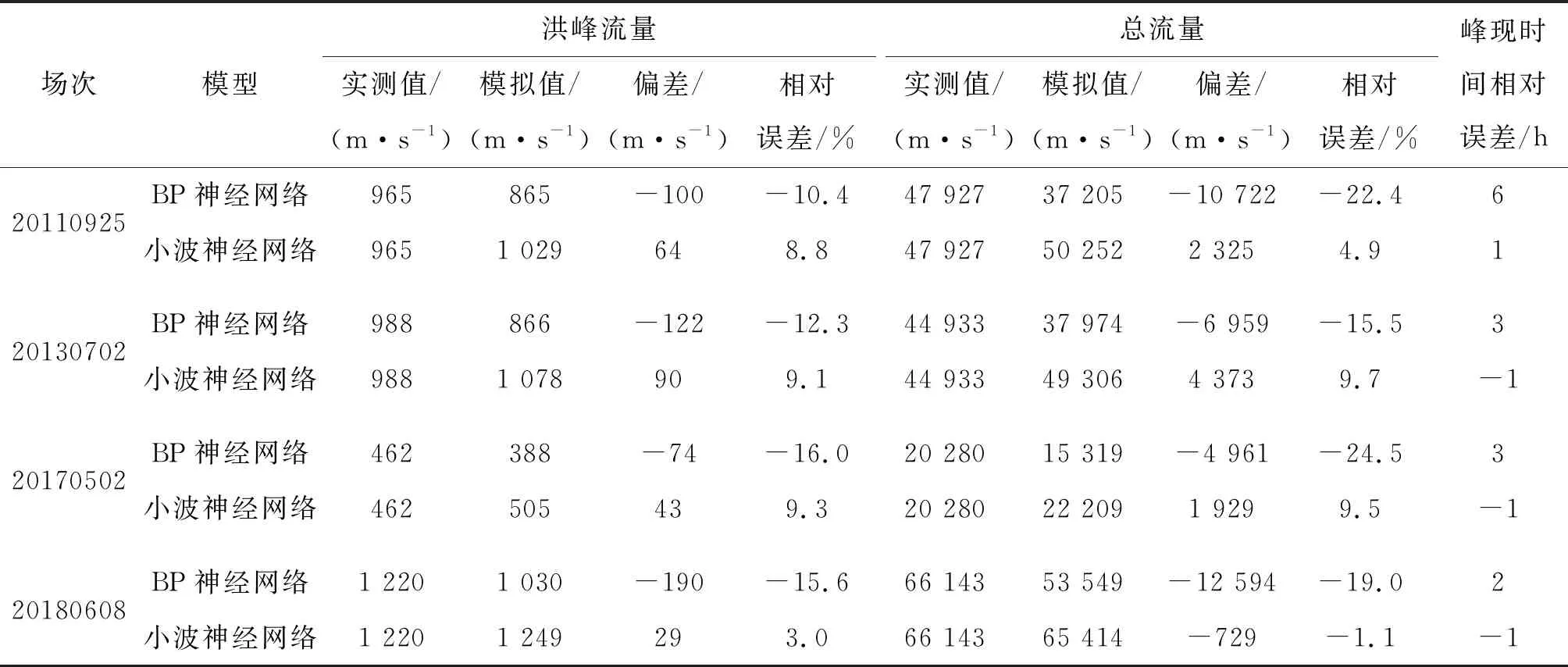
3.4 結果對比

本文利用剩余4組暴雨數據(20110925、20130702、20170502和20180608)分別進行BP神經網絡模擬和小波神經網絡模擬。模擬結果見圖3，模擬結果見表2。

由圖3可知，從定性來看小波神經網絡模擬過程相較于BP神經網絡模擬過程更貼合實測過程。從定量來看，一般根據GB/T 22482—2008《水文情報預報規范》(以下簡稱國標)規定，選用總流量相對誤差、洪峰流量相對誤差以及峰現時間相對誤差等指標來評定洪水預報的精度。

a)20110925

b)20130702

c)20170502

d)20180608

由表2給出的3個評價指標表明：①洪峰流量相對誤差，小波神經網絡模擬20110925場次誤差為8.8%，20130702場次誤差為9.1%，20170502場次誤差為9.3%，20180608場次誤差為3.0%，均不超過10%，遠遠小于國標許可誤差20%；但BP神經網絡模擬誤差較大，20110925場次誤差為-10.4%，20130702場次誤差為-12.3%，20170502場次誤差為-16.0%，20180608場次誤差為-15.6%，均超過10%，勉強滿足國標許可誤差。②總流量相對誤差，小波神經網絡模擬誤差均控制在10%以內，20110925場次誤差為4.9%，20130702場次誤差為9.7%，20170502場次誤差為9.5%，20180608場次誤差為-1.1%，遠遠小于國標許可誤差20%；BP神經網絡模擬誤差很大，20110925場次誤差為-22.4%，20170502場次誤差為-24.5%，均不滿足國標許可要求，20130702場次誤差為-15.5%，20180608場次誤差為-19.0 %，勉強滿足國標許可誤差20%。③峰現時間相對誤差，國標許可誤差小于3 h，小波神經網絡模擬在四場次中誤差均控制在1 h以內，精度較高滿足要求；但BP神經網絡模擬誤差較大，20110925場次誤差為6 h，20130702場次誤差為3 h，20170502場次誤差為3 h，20180608場次誤差為-3 h，結果均不滿足國標許可誤差。

為了得到更合理的結論，本文還采用了均方根誤差、相關系數指標和確定性系數，來評估模型的適用性與可行性(表3)。均方根誤差能顯著體現模型的優劣，值越小模型準確性越高，預報值同模擬值離散程度越小。相關系數的絕對值越接近1，預報值和模擬值相關性越強，越靠近0，相關性越弱。

表2 4個場次BP、小波模型模擬結果對比

表3 BP模型和小波模型模擬指標對比

由表3給出的3個評價指標表明：①均方根誤差，對于同一個模型，次洪總流量越大，則均方根誤差相對越大，對于同一場次，小波模型模擬誤差均小于BP模型模擬誤差，平均誤差降低了50%；②相關系數，小波模型相關系數均大于BP模型相關系數，且小波模型相關系數均大于0.90，認為有較強的相關性；③確定性系數，小波模型確定性系數均大于BP模型確定性系數，小波模型確定性系數均大于0.80，模型精度高，BP模型確定性系數變化幅度大，最低降到了0.3，模型相對不穩定精度較低。總體來說，小波神經網絡模型較BP神經網絡模型適應性更強，模擬精度上有了較大的提升。

4 結論

a)本文根據滁河流域南京段洪水預報難、預報精度偏低等實際問題，分別新建了BP神經網絡洪水預報模型和小波神經網絡洪水預報模型。通過對比總流量相對誤差、洪峰流量相對誤差、峰現時間相對誤差、均方根誤差、相關系數、確定性系數等6個指標，表明了小波神經網絡模型較BP神經網絡模型更貼合實際洪水過程，預報精度更高、適應性更強，將來可為南京市六合區的防洪減災決策提供科學的參考依據，從而更大力度地減輕強降雨對研究區造成的破壞和經濟損失。

b)小波神經網絡模型總體表現優秀，但仍有一定的改進空間，如若從優化參數、預處理樣本數據、探索多因素對洪水影響等角度深入研究洪水預報，那么小波神經網絡將成為最具前景的洪水預報實戰手段之一。

c)小波神經網絡模型耦合小波分析與神經網絡，具有結構更簡單、收斂速度更快、精度更高等優點。不僅可以應用于長系列小時洪水預測，還可應用至長序列日洪水預測、枯季徑流中長期預測等，更可以將應用范圍拓寬到各行各業實際預測中，如停車位預測、交通流量預測、股票波動預測等，解決城市生活中諸多預測問題，研究意義十分重大。