某輕型電動貨車車架有限元分析及優化*

王維偉， 鄭再象， 夏宗寶， 方劍宇

（揚州大學機械工程學院，江蘇 揚州 225000）

0 引言

隨著社會經濟的發展， 輕量化成為我國汽車產業的主要發展目標。 據相關研究， 電動汽車總質量每降低500kg，百公里能耗將降低2.75%[1]。 輕型電動貨車作為如今物流運輸重要的交通工具， 它的輕量化設計將在減少能耗、延長續航里程、提高運輸效率等方面有重要意義。車架是汽車各總成部件的裝配基體，結構及受力復雜，目前國內部分輕型電動貨車車架是由傳統燃油車車架改裝而成，總體強度和剛度偏富裕，但局部薄弱，易導致早期疲勞破壞[2-3]。 采用理論分析法很難獲得精確解，試驗法耗時耗力，因此需要借助有限元法對原車架進行仿真分析，精確獲取車架的應力和位移分布云圖， 為后續的輕量化優化提供依據。

1 有限元分析

1.1 建立有限元模型

運用CATIA 建立輕型電動貨車車架三維模型， 將模型導入有限元軟件HyperMesh 中進行前處理。 為提高計算精度和效率，對模型進行如下簡化：車架主體結構采用矩形鋼管焊接裝配而成， 部分支座采用厚度焊接而成，所涉及的板厚有：3mm、4mm、5mm、6mm 和8mm。 為方便后續的優化設計， 采用殼單元PSHELL 對車架進行網格劃分。各部件之間采用焊接或螺栓連接而成，結合實際情況，現采用剛性單元RBE2 或三角形單元CTRIA3 來模擬。 以集中質量單元CONM2 來代替駕駛室、 駕駛員及副駕、電機、離合器、變速器、傳動軸、電池、控制器等的質量，集中質量單元與支車架的連接采用剛性單元RBE2。

本文的裝載質量均以集中載荷的形式施加在相關總成上，各部位具體質量如表1 所示。

表1整車各部件質量

在劃分網格時必須要考慮結構整體的單元規模、所需的計算精度和硬件的計算能力等[4-5]。 單元尺寸選擇既要保證整體單元質量合格， 減少后續的單元質量檢查與編輯的工作量，又要盡量減少單元總量，提高計算效率。 經對比分析，將車架主體部分模型按照10mm 的單元尺寸劃分，所建立的有限元模型如圖1 所示，單元總計634 988個， 其中CQUAD4 單元為622 352 個（98.01%），CTRIA3單元為12 549 個（1.98%），RBE2 單元為69 個，CONM2 單元為18 個。材料取Q235B，其物理學特性為：彈性模量E=206.5GPa，屈服強度為235MPa，強度極限為375MPa，泊松比0.3，密度為7.83×103kg/m3。 根據第四強度理論，材料不發生塑性變形的條件為：

式中：σeq為等效應力（或者稱為Von Mises 應力）；σ1為第一主應力，σ2為第二主應力，σ3為第三主應力，[σ] 為材料的許用應力，即屈服應力。 當等效應力σeq與許用應力[σ]滿足式（1）關系時，認為此時強度滿足設計需求。

圖1 車架有限元模型

1.2 典型工況分析

對滿載運動（動態）、驅動、緊急制動、轉向、扭轉（單輪懸空）等工況進行對比分析后，取最危險的滿載彎曲、扭轉2 種工況展開研究，具體如下。

1）滿載運動：汽車在良好狀況的路面滿載勻速行駛時，忽略空氣阻力的影響，車架受到的載荷形式主要為垂直方向重力的載荷， 動載荷系數取保守值2.0。 邊界條件方面，約束左前輪X、Y、Z；右前輪X、Z；左后輪Y、Z；右后輪Z 方向自由度，釋放4 點全部轉動自由度。

2）右前輪懸空：在凹凸不平的路面行駛時，車輪會出現懸空的情況，此時車架受到較大扭矩。 由于該工況下車速一般較低，動載荷系數受車速影響較小，取保守值1.3。右前輪懸空時的邊界條件， 只需在滿載運動的基礎上釋放右前輪的約束。

1.3 仿真結果分析

1.3.1 滿載運動工況

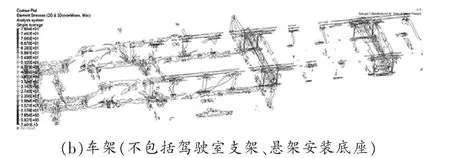
圖2 車架應力分布云圖

滿載運動工況下，車架所受的最大應力為297.6MPa，位于車架后右支座處；另外，駕駛室后左支座和前左支座應力也比較大，均接近材料的屈服極限，如圖2(a)所示。 去掉駕駛室支座、 懸架安裝支座后， 車架最大應力為78.5MPa。 圖3 為車架的位移分布云圖， 可見在Z 方向上最大位移僅為0.47mm。

圖3 車架Z 方向位移云圖

1.3.2 右前輪懸空

圖4 給出了右前輪懸空時車架的應力分布云圖（≥100MPa）。 從圖中可以看出，車架上應力比較大的地方位于駕駛室支座、中間和后電池箱與車架連接處、前懸架與車架連接處等，其中最大應力為427MPa，超過了材料的屈服極限。 如圖5 所示，車架在Z 方向上的最大位移達到了3.07mm。

圖4 車架應力分布云圖

圖5 車架Z 方向位移云圖

兩種工況仿真結果表明， 車架整體強度和剛度非常高，但局部又存在明顯不足，需要進一步優化，以滿足車架設計要求，同時可在最大程度上減輕車架的質量。

2 優化設計

2.1 確定目標函數

取質量作為優化目標，通過改變零件厚度的方式實現輕量化，不需要重新建立有限模型。 目標函數M（T）表達式見式（2）：

式中：Vi是第i 個零件的體積；ρi是第i 個零件的密度；Si是第i 個零件的中面面積；Ti是第i 個零件厚度；i 零件序號，i=1，2，3……245。

本次優化設計變量為245 個，為了減少工作量且優化后尺寸符合厚度制造規則，步長選取0.2mm。 本次優化的約束條件為剛度與強度要求， 強度要小于許用應力200MPa，最大位移范圍取[-4.0，+4.0]mm。工況選擇滿載運動工況，動載荷系數取保守值2.0，以加速度的形式加在相關總成上。

2.2 優化計算及結果分析

運用Optistruct 模塊對車架245 個部件進行優化，迭代23 次， 體 積 從4.250 97×107mm3優 化 至3.056 46×107mm3，最大位移從1.17mm 增大到了1.57mm。

優化后，245 個部件中有220 個得到了減重，7 個部件維持原有質量，18 個部件質量增加。 但零件規格明顯增多，達到20 多種，大幅提高了制造成本。綜合實際生產，對上述優化結果進一步調整， 最終將零件規格下降至7 種，質量由332kg 降低至222kg，減重率達33%。 對優化后的車架再次進行靜態力學仿真分析， 在滿載運動和右前輪懸空工況下， 車架的最大應力分別為168.3MPa 和326.2MPa， 如 圖6 所 示， 最 大 位 移 分 別 為0.68mm 和4.48mm，滿足強度和剛度需求。

圖6 車架應力分布云圖

2.3 車架模態分析

對優化后的車架進行模態分析， 并與優化前的結果進行比較分析，結果如圖7 所示。 優化后車架同階的固有頻率均小于優化前，且最小固有頻率為11.96Hz，處于路面的激勵頻率之內，但遠大于路面能量的最大激勵頻率范圍，各階固有頻率基本避開了驅動電機的激勵頻率[6-7]。

圖7 優化前后車架各階固有頻率對比

3 結論

對某輕型電動貨車車架進行有限元分析及優化，得出以下結論：

1） 改裝傳統燃油貨車車架作為電動貨車車架的方法，后者總體剛強度達到需求或偏富裕，但也存在局部薄弱的情況，需要進行優化設計。

2） 采用有限法可精確獲得車架的應力和位移分布情況，為車架設計提供理論依據。

3） 在滿足車架強度和剛度要求的前提下， 通過自動尋優，可有效降低車架的總質量。

4） 優化后，車架各階固有頻率均有所下降，但基本避開了外界常見的激勵頻率，所分析的結果是有效的。