駁船浮沉過程的力學模型研究*

楊曉寧

（大連職業技術學院交通工程學院，遼寧 大連 116035）

0 引言

隨著中國造船業與國際海運行業的發展， 運輸船舶以及海上結構物朝著越來越大型、 結構越來越復雜的方向發展，其設計、建造、下水以及營運均面臨著極大挑戰。大型船舶或者結構物下水， 是使其從陸地移動到水中進而實現其價值的重要環節， 目前應用比較廣泛的形式有重力式下水、自漂浮式下水和機械化下水三種，其中利用駁船實現各種結構物下水的方式不受場地、下水區域、船塢能力等諸多因素的影響，適用于各種大小、類型的船舶及海上結構物的下水[1]。 本文從力學角度出發，對駁船浮沉過程進行研究，以保證整個下水作業安全。

1 駁船浮沉過程中性能計算

1.1 駁船浮態、初穩性計算方法

圖1 船舶坐標系

如圖1 所示建立船體坐標系：選取三個相互垂直的基本平面中線面、中站面和基平面，三個面的交點為坐標原點O； 中線面與基平面交線為X 軸， 并指向船首方向為正； 中站面和基平面交線為Y 軸， 并指向船右舷方向為正；中線面和中站面交線為Z 軸，并指向上為正。 船舶浮態通常用首尾吃水來表示，計算船舶吃水，首先需計算船舶的排水量△：

式中，W0是駁船的空船重量，為固定重量；∑P 是其它重量，為變動重量，與其它船舶相比，駁船沉浮過程中上駁產品的重量以及壓載艙的壓載水量為主要變量。

理論證明，船舶在小角度縱傾時，縱傾軸過初始水線面漂心的橫軸，在排水量一定時，其復原力矩計算方法如下：

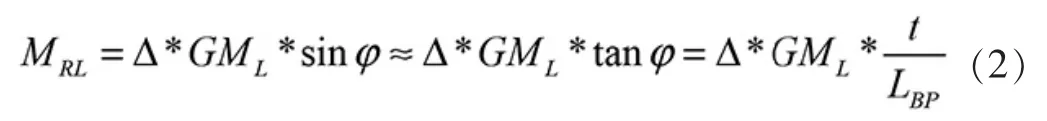
式中， MRL是復原力矩；GML是初穩性高；t 為吃水；LBP是垂線間長。

令t=1cm，則：

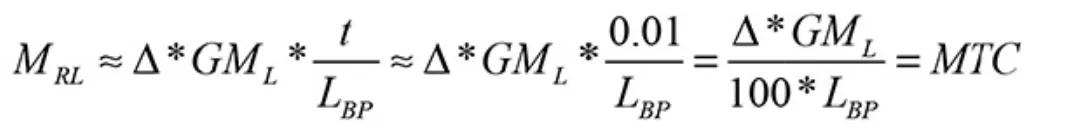
式中：MTC 是船舶為每厘米縱傾力矩，即當船舶吃水差改變1cm 時，船舶本身所具有的縱向復原力矩，可利用船舶的靜水力曲線圖或靜水力參數表得到。

因此，吃水差可按下式計算：

式中：xb是船舶浮心距離船中的距離， 由靜水力曲線圖中查得；xg是船舶重心距離船中的距離， 可將船舶各項重量重心按以下公式計算得到。

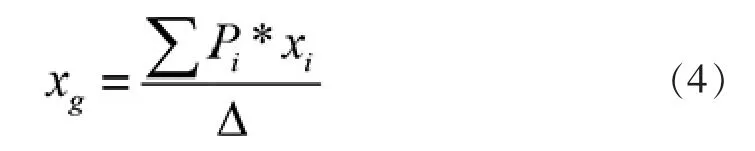
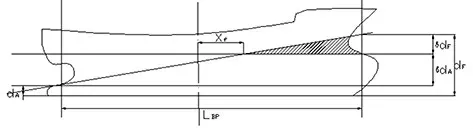
圖2 船舶縱傾時吃水示意圖

由船舶縱傾吃水示意圖2 不難看出：

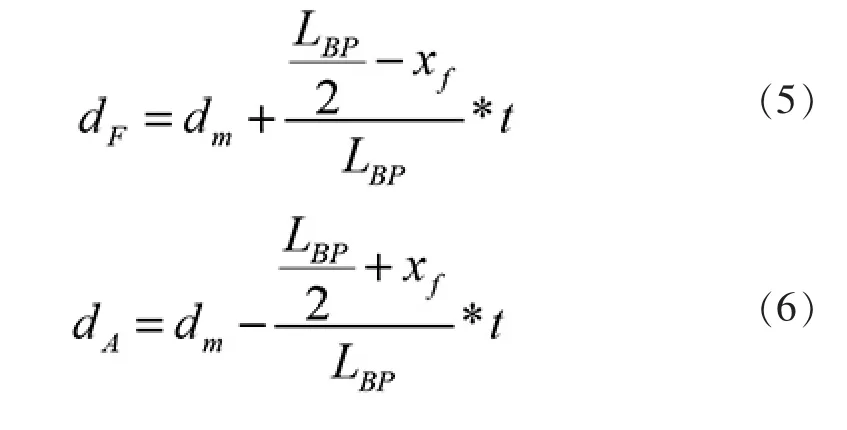
式中：dA為尾吃水；dF為首吃水；dm為當前吃水的平均值，可由靜水力曲線查得。

駁船的初穩性計算公式為：

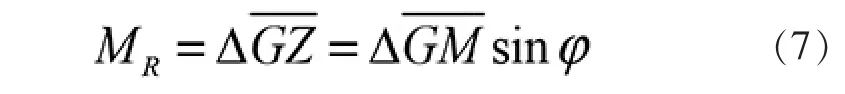
1.2 駁船強度計算

船舶在水上漂浮，重力和浮力大小相等方向相反，整體處于一個平衡的狀態，但是，將船舶分成若干個小的區域來看，會發現船舶在任何局部受力中，重力和浮力是不能平衡的，正是由于船舶局部受力不均勻，會導致船舶內部產生剪力和彎矩。 因此船舶強度是影響船舶正常運營的一大要素，如果在船舶營運過程中，忽略強度計算，就會造成船舶結構的破損甚至船體的斷裂[2]，尤其是駁船沉浮過程中的配載過程，由于壓載水量的大幅度調整，載荷的變化對船體強度影響是巨大的。 為了保證配載過程中，駁船結構完整，避免對其船體造成的不良影響，必須實時計算其強度并予以校核。

將駁船的浮力載荷曲線和重力載荷曲線疊加， 得到駁船的外載荷分布：

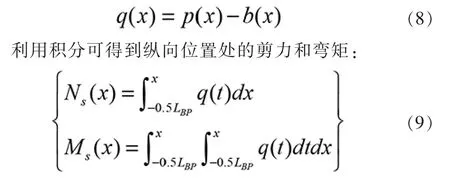
計算完成后， 按照規范要求對強度校核點進行校核即可。

2 駁船沉浮過程中力學模型

利用駁船完成產品下水主要分為兩個階段， 第一階段為產品從碼頭上駁到駁船， 第二階段為駁船在指定海域下沉，完成產品下水。 兩個階段受力情況不同，因此應分階段進行分析。

2.1 產品上駁階段

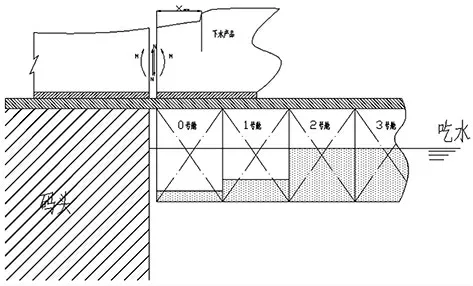
圖3 產品上駁示意圖

產品上駁過程示意圖如圖3 所示，將上駁產品和駁船作為兩個獨立的研究對象，分別考量。 一方面，對上駁產品來說，如果能夠保持駁船上表面與碼頭地面齊平，其上駁過程只是在做平面拖拽運動， 產品內部不會產生由于外力大幅變動帶來的剪力和彎矩變化， 整個過程是安全的。 另一方面，對駁船來說，可將產品上駁視作裝卸載荷，配載過程只需要依潮水的變化調整壓載水量，使得駁船達到平衡條件即可。 綜合上述兩個方面的分析內容，可以將配載過程簡化為調整駁船的壓載水量，使駁船處于理想的浮態，同時滿足其總縱強度的要求即可[3]。 考慮用優化算法和平衡方程方法對配載過程進行求解。

2.1.1 優化算法

將整個產品上駁過程分解為若干個連續的節點，可知配載的實質是通過實時調節壓載艙的壓載水量，來平衡每個節點上駁產品的重量，為保證上駁過程的連續性，每個節點配載時間越短越好[4]。 由此可見，可以將配載過程歸結為求解約束最優化問題：設置各個艙室的調載水量x 為自變量，調水量的絕對值求和為目標函數，顯然，當調水量絕對值求和最小時，配載的時間最短，該方案即為最優[5]。對該優化模型中的限制因素即為力和力矩的平衡， 同時，各個艙室的調載水量必須在艙容范圍之內，即不允許大于艙室最大壓載水量，同時不小于空艙時殘余水量。 利用懲罰函數法或其他優化方法，即可對該優化問題求解[4]。

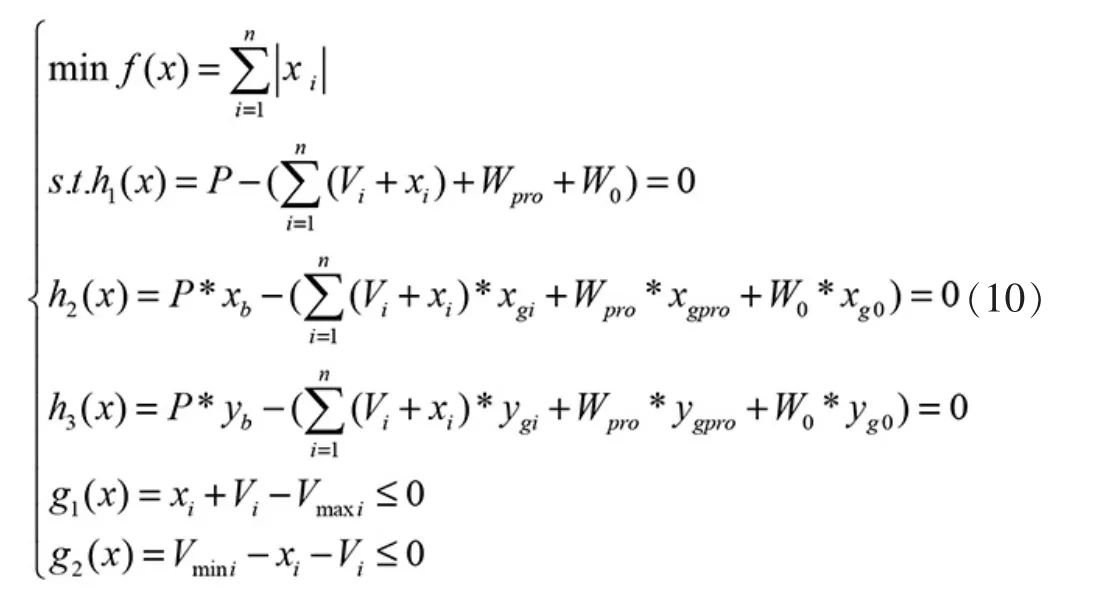
2.1.2 平衡方程法

從配載的實質出發，產品上駁過程，實質是通過調節駁船壓載艙中的壓載水量， 來抵消產品上駁部分重量，使得駁船達到力和力矩平衡，即：重力和浮力平衡，縱傾力矩和橫傾力矩平衡。 依此可建立平衡方程組如下：

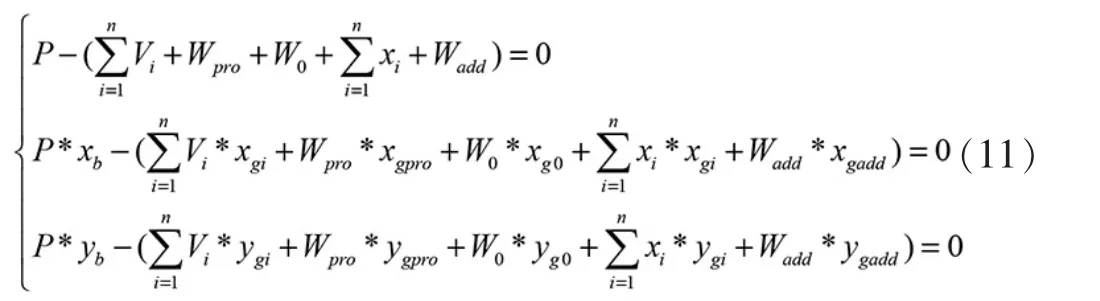
可見，該方程組有三個方程，因此最多只能限制未知數的數量為三，才能求解。 假定在駁船的n 個艙室中只有3 個進行調載，其它艙室水量保持不變，便可以得到個調載方案，依上述方程組很容易便能求得結果。將上述個方案的配載方案進行比較，將每個方案的三個調載水量絕對值求和，最少者為最終方案。

通常來說，上駁產品和駁船均為左右對稱結構，調載過程中，只需在駁船橫向對稱調節壓載水量，即可保證在上駁過程中的橫向傾斜力矩零。 因此上述問題可進一步簡化為兩個方程組求解兩個未知數。 另外，駁船不同于普通運輸船舶，其線形和結構簡單，壓載艙室具有明顯的行列規律，因此，配載問題可以進一步簡化為求解m 列中任意兩列艙室調載的問題，即在Cn2個方案中選取最優的方案。 將調載的列確定以后， 將該列調水量平均分配到左右對稱艙室中即可完成配載。 相對調節三個艙室來說，這種配載方案使得調載水量以及駁船壓在艙內水量分布更均勻， 對其結構與強度更為有利。

2.2 產品下水階段

產品上駁完成之后， 駁船會將產品移運到指定海域后下沉，完成產品下水。 在下沉過程中，為了避免產品滑落水中，造成嚴重后果，應避免駁船產生較大傾斜，最理想的狀態是始終保持駁船處于正浮。 如圖4 將下沉過程分兩個階段進行力學分析：第一階段，吃水1 狀態到吃水2 狀態，這個過程，產品重量重心未發生任何變化，因此其作為載荷對駁船的受力情況沒有影響， 駁船的配載只需通過調節壓載水量來抵抗吃水增加引起的浮力變化[5]；第二階段，吃水2 狀態到吃水3 狀態，由于產品開始進入水中，浸水部分勢必會產生浮力，因此產品作用在駁船上的力隨浸水深度在實時變化，駁船調載時，需要將這部分內容予以考慮。 最后，當產品吃水達到能夠完全支撐自身重力時，駁船便不再受到來自產品的壓力。 上述各階段中，雖然受力在不斷變化，但產品相關重力、浮力等計算完全可以按照產品手冊迅速得到， 因此配載過程與產品上駁階段并無實質差異， 而上駁階段求解方法同樣適用于本階段，不再贅述。

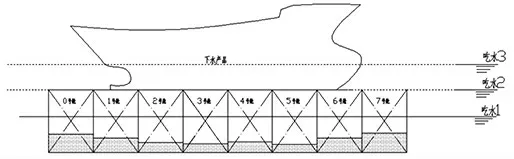
圖4 產品下駁示意圖

3 計算實例

從工程實際出發， 本文采用求解平衡方程的方法對某駁船上駁階段中的某一時刻進行計算。 該駁船的數據如下：船長122.4m，船寬59.8m，型深7m，空船重量6 292t，空船中心縱向、橫向和垂向坐標分別為-0.375m、0m 和4.944m。 本步調載初始數據：產品已上駁部分重量為666t，重心縱向坐標為-47.686m，浮心縱向坐標為0m，當前時刻潮高331.5cm，結束后潮高333.5cm，本步需上駁產品重量149t。 該船的壓載艙布置情況如圖5 所示。

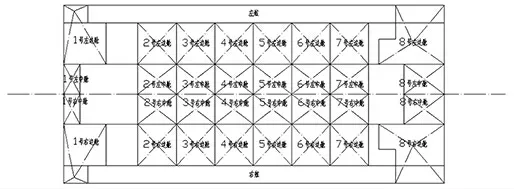
圖5 算例駁船艙室布置圖

利用計算機程序， 輕松求得本步調載的最優方案為：在2 號艙室左右中艙各排水58t， 在7 號艙室左右邊艙各注水41t，配載后駁船的艏左、艏右、艉左、艉右四點吃水均為4.049m， 其橫穩性高為45.611m， 縱穩性高為322.418m，最大剪力為6.67E+02tN，最大的彎矩為1.18E+04t*m。 可見， 在本步調載中， 由于潮水的升高需要注水115t，由于產品進入需要排水149t，二者求和，恰好等于四個調載艙室共排水34t，同時船舶個性性能指標均滿足規范要求，由此，證明本方法安全可靠。

4 結語

本文從配載的實質出發，提出兩種解決駁船在沉浮過程中的配載方法。 計算結果證明方法具有實際的可操作性，并滿足工程作業要求。 另外，可將該模型進行適當處理，將其推廣到其它運輸船舶的調載作業中去，具有較高的實用價值。