基于改進人工蟻群的智能巡線機器人路徑規劃

劉二根，譚茹涵，陳藝琳，郭 力

（華東交通大學1. 理學院； 2. 系統工程與密碼學研究所，江西 南昌 330013）

隨著疫情的持續蔓延，“無接觸式”一詞成為了當下熱點。生產生活中部分工作已由機器人替代人執行，抗疫機器人可以在一線檢測來訪人員體溫，安防機器人能提醒司機掃碼登記，送餐機器人在隔離區提供遠程配送等，在特殊時期，智能巡線機器人的投入使用在人與人的安全距離上多建立了一道防線。而路徑規劃是智能機器人的關鍵技術之一。

路徑規劃是指機器人在規劃好的環境中搜索出一條或路徑長度最短，或耗時最短的最優路徑，還應根據對環境信息的把握，遵循一定的性能要求，使得路徑與障礙物無碰撞。 蟻群、人工勢場、遺傳算法、A*、Dijkstra 等是常用的路徑規劃算法。 Khatib 等[1]提出人工勢場算法，是傳統算法中較成熟且高效的規劃方法，但容易陷入陷阱和局部極小點，徐小強等[2]采用人工勢場法規劃路徑，障礙物和必經點分別對機器人產生排斥力和吸引力，在此過程中,機器人對障礙物的斥力比較敏感，使得路徑易在目標點附近游離，無法達到目標點。 張馳等[3]將勢場算法結合蟻群，重建啟發函數，更新了信息素規則，從局部最優解中解脫。 王小會等[4]通過嵌入Dijkstra 算法實現一種經過必經點的最短路徑。 曹祥紅等[5]利用Dijkstra 算法搜索到全局路徑后，導入ACO 算法進行路徑優化，提高了效率，但沒有考慮陷阱的情況。Hart[6]提出了A*算法，引入估價函數，如果估價函數等于最短距離，那么搜索將嚴格按照最短路徑進行，此時的搜索效率最高。 羅漢杰等[7]選擇曼哈頓距離作為估價函數，計算出最佳路徑，但未對軌跡做平滑處理，無法滿足現實情況下的機動性。 余文凱等[8]利用K-Means 對地圖進行分區處理，根據聚類結果，對評價函數和節點選擇方式進行改善，改善了平滑度，搜索效率更高。蟻群算法1991 年由Dorigo 提出，吸收了螞蟻的行為特性，根據信息素濃度進行路徑的選擇，算法魯棒性較強，設置簡單，但收斂速度慢，沒有考慮地形的因素。 左敏等[9]引入自適應遷移概率函數，提高了算法的收斂速度，但沒考慮平滑度的需求。

基于對路徑規劃問題中障礙物的繞過、路徑平滑度、尋路效率等因素的考慮，采用A* 結合ACO 算法的組合模型對機器人路徑進行規劃，利用A* 算法的全局搜索能力，找出兩點之間最合適的路徑，在進行多點規劃時，采用改進后的蟻群算法求解多點之間最優路徑。

1 全局路徑規劃

1.1 環境建模

在仿真環境中， 障礙物是不可避免的參數，本實驗采用柵格法對環境進行模擬，將環境劃分為二值網格單元見圖1，其中柵格大小暫定為1，實際行駛過程中會根據機器人大小進行設定。 將巡線地圖設為60×60 的柵格圖，其中黑色區域為地圖中的障礙物區域，白色區域為安全區域。 其中的散點代表著巡線機器人要巡視的地點。

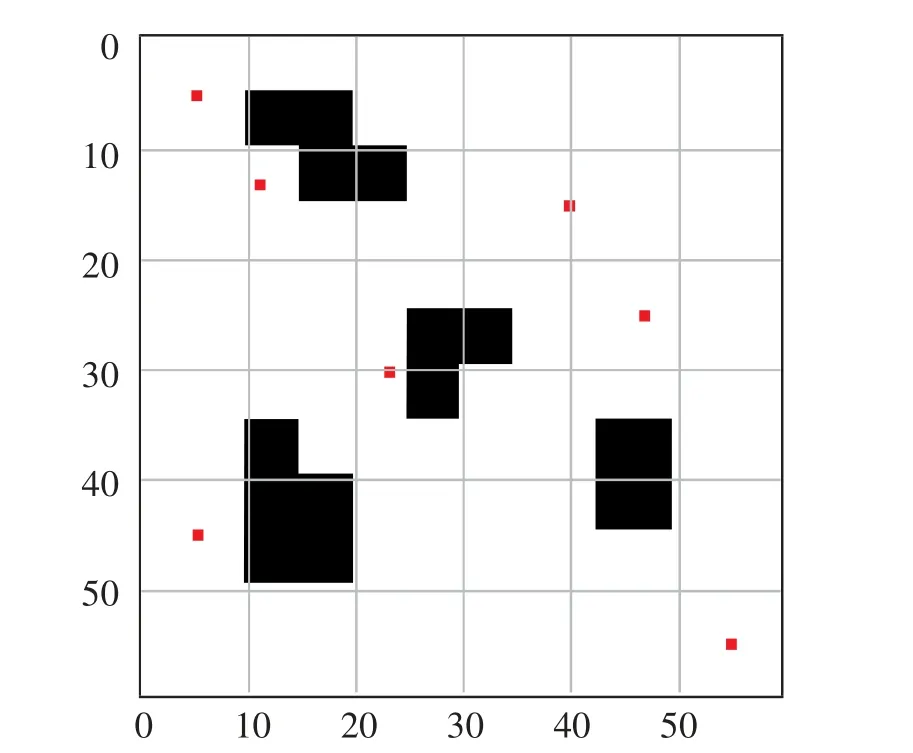
圖1 環境仿真柵格圖Fig.1 Environment simulation grid

1.2 A*算法原理

A* 為一種多角度進行搜索的全局尋路算法，選取在當前位置周圍F 值最小的點為路徑的下一步。 F 為代價函數，計算公式為

式中：G 為從起點移動到指定位置的移動代價,取橫向及縱向為10，對角線為14；H 為從指定位置移動到終點的估算成本，其中路徑忽略障礙物，當前選用Manhattan 方法進行估算

計算當前位置橫或縱向移動到達終點所經過的方格數。

A*算法規定了路徑的角度，傳統算法有8 個角度對外擴展。 具體步驟如下：

①設定open 表存放當前點可能要經過的下一個點，設定close 表存放不能經過的點；

②搜索與八個位置對應相鄰的柵格，將當前位置設置為父節點，設為點A；

③排除掉障礙物和已經走過的位置，剩余位置設置為子節點，都放入open 列表中，進行F 值的計算，將子節點中F 值最小的點，設為點B，加入close 列表；

④將B 點設置為父節點后重復操作；

⑤當發現此點的子節點已經在open 列表中，假設為點C，則檢查由點A 直接到點C 是否會比A-B-C的路線更優，若是，則退回一步，重新將A 設置為父節點，此時B 點已進入close 列表，不會參與進行下一點的路徑選擇。

從圖2 中A* 算法的路徑選擇可以明顯看出路徑結果角度生硬，轉折點過多，不夠平滑。 對此路徑進行平滑處理：遍歷路徑上的點，若是兩點之間無障礙物，則可直接連接。 基于此條平滑準則，需要對兩點之間經歷的柵格進行判斷，判斷其是否有障礙物。

1.3 障礙物判斷

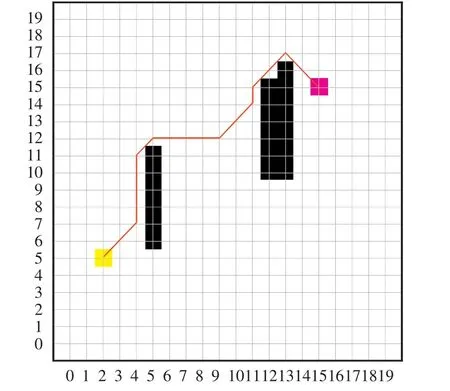
圖2 A* 算法尋路結果圖Fig.2 A* algorithm path finding result

①計算兩點之間直線方程f；

②由于柵格是以整數坐標為中心， 上下左右距離中心0.5 個位置的正方形， 取距起點縱坐標0.5 個位置為第1 個測量點， 每距離1 個位置進行測量，生成列表y=［y1，y2，…，y3］；

③基于直線方程，生成列表x=［x1，x2，…，x3］；

④判斷y 中每2 個相鄰的值間隔幾個柵格

num=math.ceil（x［i］-）-math.floor（x［i-1］） ( 3 )其中，math.ceil 是向上取整，math.floor 是向下取整。

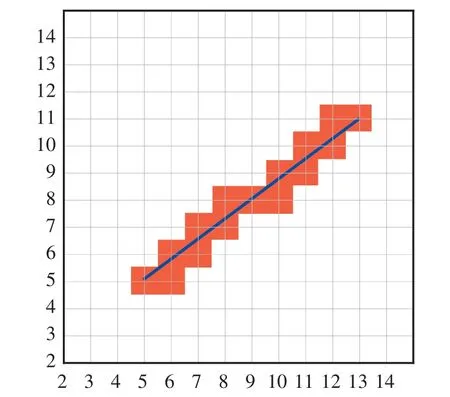
圖3 一條直線經過的柵格Fig.3 A grid with a straight line

平滑后的A* 算法不僅能使路徑更流暢，還能成功脫離“陷阱”，由圖中可看出，在某個障礙物附近徘徊的線條平滑后成功出逃。

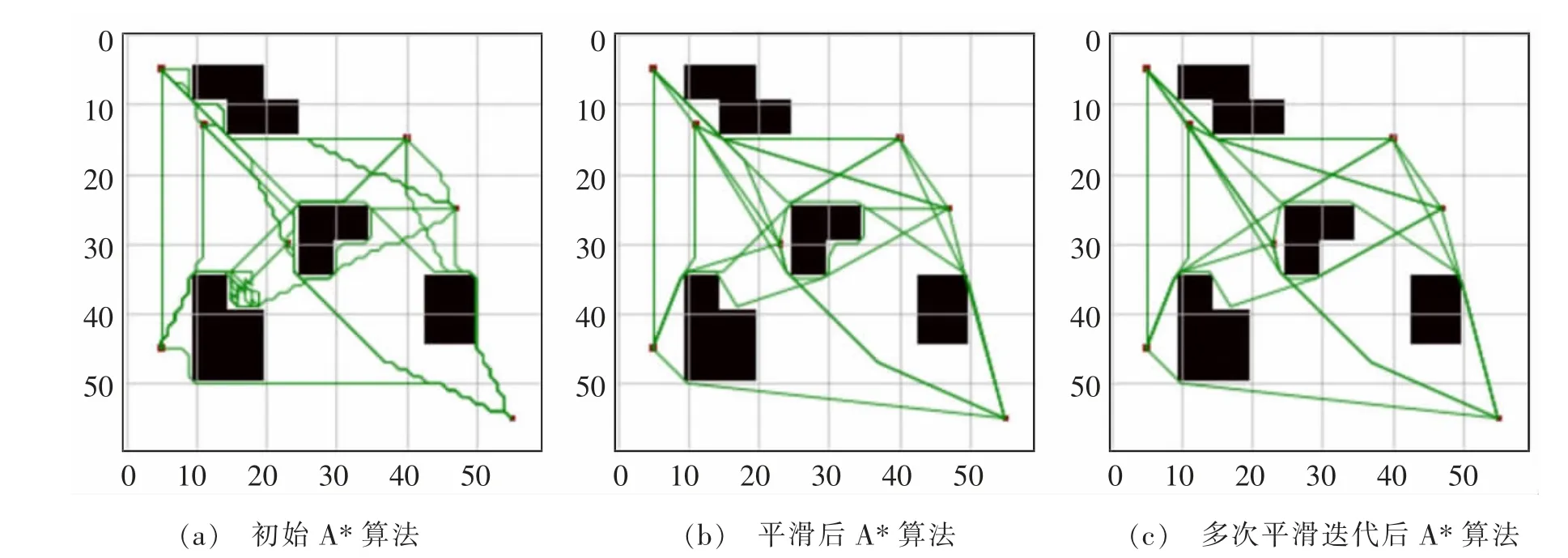
圖4 不同A* 算法結果比較Fig.4 Comparison of results for different A* algorithms

2 最優路徑規劃

2.1 實驗蟻群算法原理

蟻群算法是一種啟發式優化算法，蟻群在尋找食物時，總是能找到一條從食物到蟻穴的最短路徑，信息素在其中發揮了很大作用，螞蟻走過的路徑都會留下信息素，剩余的螞蟻選擇路徑時會受信息素的濃度影響，在岔路口時，傾向于選擇濃度更高的一側。

在A*算法找到全局路徑后， 構建信息素矩陣， 信息素矩陣中的元素會在迭代過程中隨著路徑不斷變化，迭代完成后，信息素濃度最高的路徑就是最優的結果。

傳統蟻群算法對信息素處理分為全局和局部兩種，全局處理是在螞蟻循環完整個路徑后，對整個信息素矩陣進行更新，局部信息素處理是在螞蟻每完成一步后更新信息素。本實驗引入雙信息素策略，局部與全局同時進行，能有效克服傳統蟻群易陷入局部最優解的問題。

2.2 算法描述

1） 設置螞蟻數量，輸入必訪問點列表，設置迭代次數，初始化點之間的距離矩陣，信息素矩陣，啟發函數矩陣；

2） 將螞蟻放在不同點上，盡量保證螞蟻的起始點不同，并記錄下螞蟻訪問的點下標，將其加入禁忌表，表示下次不會再重復訪問此點；

3） 根據狀態轉移概率對下一次訪問點做出選擇

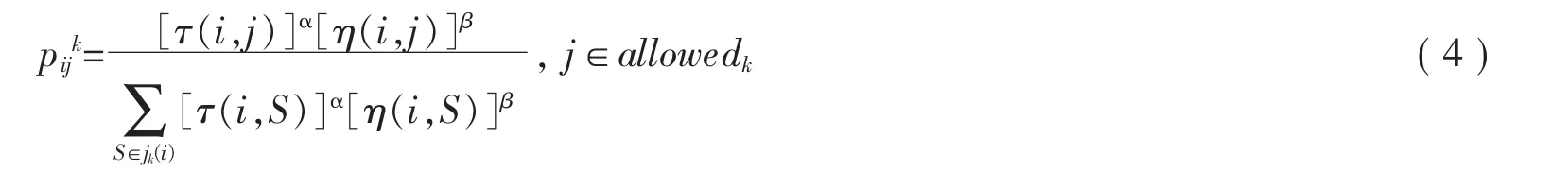
式中：α 為信息啟發式因子；β 為期望啟發式因子；τ 為信息素濃度；η為啟發式信息，取值為

一般取為點間距離的倒數；

4） 在自然界中，螞蟻遺留的信息素會隨著時間流逝而揮發，模擬此過程，更新信息素矩陣，螞蟻移動到下一點后，對信息素進行局部更新

5） 重復以上步驟，一直到路徑形成閉環，即螞蟻回到起始點。 對表現最優的精英螞蟻采用全局信息素更新策略

式（6）中：ρ 為人為定義的信息素揮發率，一般位于0～1 之間，由于實驗所用到的地圖較小，選擇較低的揮發率能達到較好的實驗結果，故選取ρ 為0.1。 全局更新策略不作用于所有螞蟻，只對每次循環中的精英螞蟻（路徑最短）使用，這樣做可以減少迭代次數，加快搜索效率。

3 實驗與比較

采用局部信息素更新策略的蟻群算法稱為蟻量模型，而使用全局信息素更新策略的蟻群算法稱為蟻周模型。 分別對蟻量模型、蟻周模型及雙信息素蟻群算法進行實驗，對改進蟻群算法的兩種信息素加以權重，經過多次實驗，確定全局信息素權重為1，局部信息素權重為2。

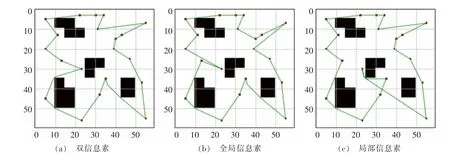
圖5 不同ACO 算法結果對比圖Fig.5 Comparison grid of results for different ACO algorithms

表1 基于不同數目必經點算法所用時間結果比較Tab.1 Comparison of time results for algorithms based on different number of required points s

從算法時間比較表來看， 雙信息素策略對算法時間影響不大，與另兩類蟻群算法相比，時間差距在0.5 s 內。 在效率對比圖上有15 個點以及20個點的三種蟻群算法最優解進化過程， 可以看出改進蟻群算法比兩種傳統算法收斂更快， 且傳統算法易陷入局部最優，改進算法得到的路徑更優。

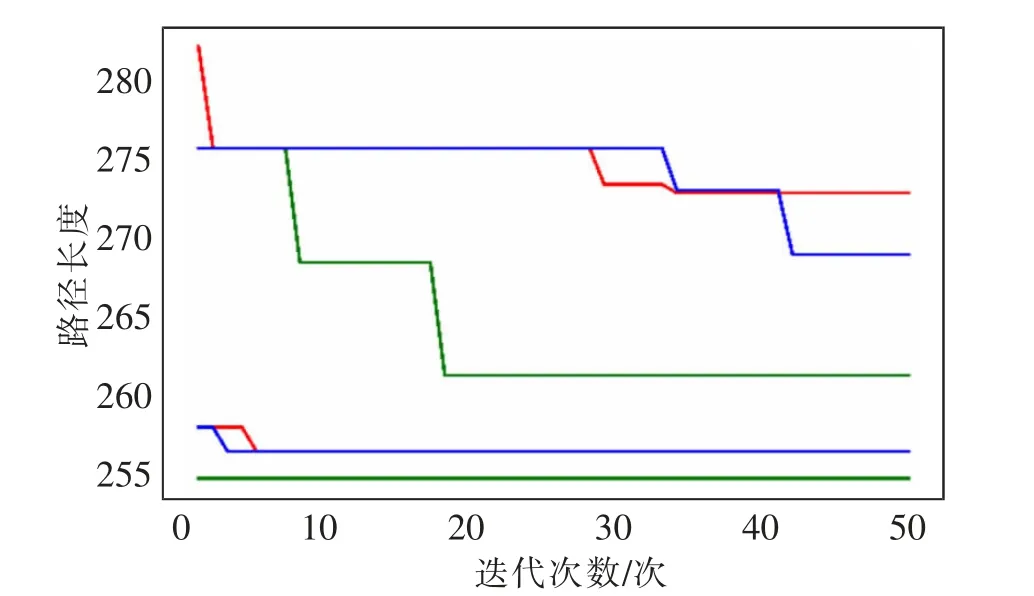
圖6 效率比較圖Fig.6 Comparison chart of efficiency

5 結論

本文利用A* 算法得到繞過障礙物的全局路徑，平滑后成功繞過“陷阱”，且得到結果更優的全局路徑，再引進雙信息素改進傳統蟻群算法，有效克服了蟻群算法易陷入局部最優解的缺陷，使得性能顯著提升，且必經點越多，路徑越復雜，優化效果越明顯。