某水電站泄洪洞和引水隧洞并行段最小凈距研究

江 華

(江西省水利水電建設有限公司，江西 南昌 330000)

1 工程背景

某水電站是一座以發電為主，兼有防洪和灌溉等功能的綜合性小型水利工程，也是遼寧省十三五重點水利工程項目之一，電站壩址以上集雨面積293km2，按照百年一遇洪水標準設計，千年一遇洪水標準校核，設計水位293.5m，對應庫容0.87億m3。水電站的主要建筑物包括混凝土重力壩、副壩、溢洪道、泄洪洞以及引水發電系統。受地形和地質等方面因素的制約，電站的泄洪洞和發電引水隧洞均設計于大壩的左側，且需要兩隧洞之間的間距盡量小，以便在線路設計時能夠盡量避開左側山體中的SK03斷層。但是，該并行段基本處于弱風化的安山玢巖地層結構中，局部分布有輝綠巖和強風化流紋巖，洞身段的圍巖類別以Ⅲ類為主，末端圍巖類別為Ⅳ類，強度較低、穩定性差，兩者在施工過程中的影響不容忽視[1]。在以往的研究中，主要是考慮新建隧洞對原有隧洞的影響，而并行施工過程中面臨的力學問題無疑更為復雜[2]。基于此，本次研究通過數值模擬的方法，對泄洪洞和輸水隧洞施工過程中的相互影響和應力位移特征進行研究，以確定泄洪洞和引水洞的最小間距，為工程的設計和順利施工提供參考。

2 有限元計算模型的構建

2.1 軟件選擇

midas GTS NX 2019是一款針對巖土領域研發的通用有限元分析軟件，作為一個全面有限元分析軟件包，可處理各種巖土工程設計應用，支持靜力分析、動力分析、滲流分析、應力-滲流耦合分析、固結分析、施工階段分析、邊坡穩定分析等多種分析類型，適用于各種實際工程的準確建模與分析，并提供了多種專業化建模助手和數據庫[3]。同時，該軟件作為新一代巖土分析軟件，應用了最尖端的圖形和分析技術，可以支持最新的OS圖形用戶界面。直觀的界面將使新用戶能夠輕松地將軟件集成到他們的工作流程中[4]。此外，該軟件還集成了混合網格生成功能，該功能可創建使用六面體和四面體元素的最佳組合的網格集，在建模復雜幾何形狀的較尖銳的曲線和拐角時更有效[5]。鑒于該軟件的優勢和本次研究的實際需求，利用midas GTS NX 2019進行研究對象的有限元模型構建。

2.2 模型的構建

為了保證模擬結果的科學性和準確性，結合相關研究經驗，確定模型的計算范圍為隧洞的上下各40m，左右各50m，模型的長、寬、厚分別為124m、85m和30mm[6]。其余圍巖部分利用相應的壓力荷載施加于模型上部邊界，兩隧洞之間的間距設定為15m。對隧洞的支護結構和周邊的圍巖部位進行網格加密處理。考慮圍巖的塑性變形，圍巖巖體采用Druncker-Prager 模型本構的實體單元[7]；隧洞的初支結構采用彈性本構單元，錨桿則采用彈性本構植入式桁架單元。整個模型劃分為96681和計算單元，102420個計算節點，圍巖的網格單元劃分示意圖如圖1所示。

圖1 圍巖有限元模型示意圖

2.3 計算參數

結合相關研究成果和工程實際情況，在數值模擬分析中進行如下假定：研究洞段的圍巖為各向同性材料，模型采用Druncker-Prager準則進行圍巖和支護結構的計算研究，在計算過程中不考慮構造應力，僅考慮自重應力[8]。模擬計算中采用的材料物理力學參數見表1。

表1 圍巖物理力學參數

2.4 計算工況

本次研究的主要目的是針對不同隧洞凈距條件下的圍巖應力位移影響模擬計算，獲得最佳泄洪洞和輸水洞凈距。顯然，影響隧道凈距的因素較多，圍巖條件、埋深條件以及開挖和支護方法均會產生比較顯著的影響。基于此，本次研究以背景工程地質環境條件和相關工程設計為基礎，保持其余因素不變，分別建立凈距為隧洞直徑0.5倍、1倍、1.5倍、2倍、2.5倍、3倍等六種不同凈距的有限元模型，通過凈距對隧洞位移和應力的影響模擬，獲得最佳凈距值。由于泄洪洞和引水洞的直徑均為4.2m，計算上述六個凈距值并取整后分別為2m、4m、6m、8m、10m和12m，分別記為工況1至工況6。

3 計算結果與分析

3.1 圍巖特征點位移計算結果與分析

利用上節構建的有限元模型，對不同工況下的隧洞圍巖總位移進行計算，在計算結果中獲取泄洪洞和輸水洞的拱頂、底板、左拱腰和右拱腰四個關鍵部位的位移值，結果見表2。由表中的計算結果可知，隨著泄洪洞和引水洞凈距的不斷減小，兩隧洞各部位的總位移值均呈現出不斷增加的態勢。但是，當泄洪洞和引水洞凈距大于等于6m時，增加的速率相對較小，各部位在不同工況下的位移值比較接近；當凈距小于6m時，位移值呈現出迅速增加的態勢，各部位的位移值急速增大。由此可見，泄洪洞和輸水洞的最小凈距應該以6m為宜[9- 12]。

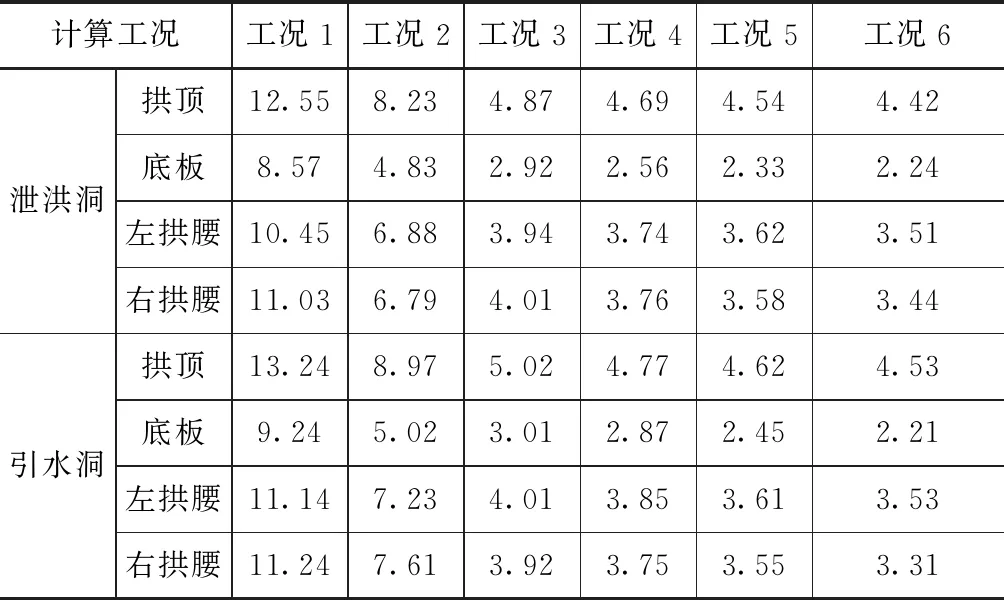
表2 圍巖總位移計算結果 單位：mm

3.2 中巖應力計算結果與分析

由于泄洪洞和引水洞之間的巖體受開挖影響較大，同時也是隧洞建成后的重要受力部分，因此在研究中利用上節構建的有限元模型，對不同工況下的中巖Von-Mises應力進行計算。在計算結果中提取8個關鍵點的計算結果(特征點位于中巖中線，最高點高于拱頂1m，最低點低于底板1m，所有特征點呈等距分布，特征點自上而下分別編號為1- 8)，并繪制出如圖2所示的Von-Mises應力變化曲線。由圖可知，各個特征點的Von-Mises應力隨著凈距的減小而增大，位于拱腰部位的特征點4和特征點5的表現最為明顯。從不同工況的結果對比來看，當凈距小于6m時，應力增大的速率明顯偏大，說明中巖的應力疊加效應十分顯著；而凈距大于6m時，應力的變化較為平緩。綜上，從中巖應力特征來看，最小凈距應該為6m[13- 15]。

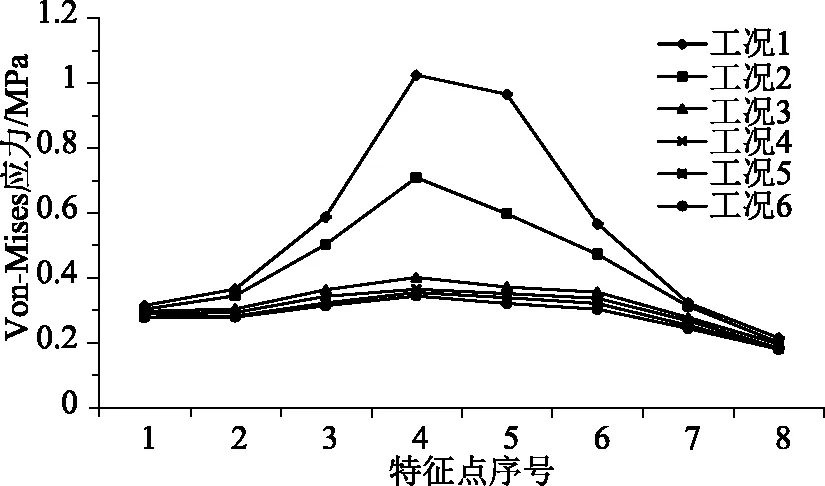
圖2 各工況Von-Mises應力變化曲線

3.3 塑性區特征計算結果與分析

利用上節構建的有限元模型，對不同工況下隧洞開挖之后的等效塑性應變進行計算，根據計算結果，繪制出如圖3所示的最大等效塑性應變值隨凈距的變化曲線。由圖可知，圍巖的最大等效塑性應變值隨著凈距的減小而增大，當凈距小于6m時，增大速率十分迅速，當凈距大于6m時增加的速率比較平緩。由此可見，當凈距小于6m時，凈距為圍巖塑性區的分布影響較大，容易造成中巖塑性區的貫通，當凈距大于6m時，凈距對塑性區的分析影響較小。因此，從塑性區分布來看，泄洪洞和引水洞的最小凈距應以6m為宜。

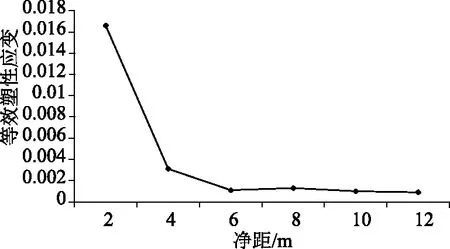
圖3 等效塑性應變隨凈距變化曲線

4 結論

此次研究以某電站左岸的泄洪洞和引水隧洞并行段為例，利用數值模擬的方法對并行水工隧洞最小凈距問題進行研究分析，獲得的主要結論如下：

(1)隨著凈距的不斷減小，隧洞圍巖的總位移值不斷增加；當凈距小于6m時圍巖的位移值急速增大。

(2)隧洞中巖各個特征點的Von-Mises應力隨著凈距的減小而增大，當凈距小于6m時，增大的速率明顯偏大，說明中巖的應力疊加效應十分顯著。

(3)圍巖的最大等效塑性應變值隨著凈距的減小而增大；凈距小于6m時，凈距為圍巖塑性區的分布影響較大，容易造成中巖塑性區的貫通，當凈距大于6m時，凈距對塑性區的分析影響較小。

(4)綜合研究成果，泄洪洞和引水洞的最小凈距應以6m為宜，可以為具體的工程設計提供參考。