基于極限平衡分析法的公路土質邊坡穩定性分析

孟 澤 彬

(山西路橋集團隰吉高速公路有限公司，山西 太原 030006)

0 引言

公路土質邊坡在外力荷載以及地下水運動、地震等內力作用下，邊坡的內部某一位置上的滑動力超過了土質本身的抗滑力，將會失去原有的邊坡穩定性。邊坡失穩是一種十分嚴重的災害，具有較大危險性，威脅著人們的安全[1]。由此認為，公路土質邊坡穩定性分析十分必要，不僅可以找出潛藏的危險，也能夠為社會經濟發展提供保障。作為巖土工程中的重要研究項目，分析方法涉及到周邊房屋、道路、礦山以及水利水電等諸多工程領域。影響到邊坡穩定性的因素較多，因此具有不確定性，在實際分析中較為復雜，此次分析中將極限平衡分析法應用于邊坡穩定性分析中，可有效提高分析計算結果的精確度。

1 基于極限平衡分析法的公路土質邊坡穩定性分析方法

在設計基于極限平衡分析法的公路土質邊坡穩定性分析方法時，應將傳統的極限平衡理論作為基礎，對公路土質邊坡進行條塊劃分，并遵循如下原則：第一，假設邊坡的穩定性安全系數為Wd，且Wd的定義應將土質的抗剪強度指標降低；第二，公路土質邊坡的各垂直條塊的最底側和最外側應當滿足Tresca屈服準則和Mises屈服準則，不同的是，條塊的底部處于極限破壞狀態，公路土質邊坡中失去穩定性的滑體與各個條塊應同時滿足力的平衡以及力矩的平衡條件；第三，考慮到土質邊坡中含有大量的孔隙，因此，進行極限平衡分析時，要將孔隙中的水壓力、地震力以及外界荷載造成的影響進行綜合的考慮[2]。

1.1 構建邊坡受力模型

在構建邊坡的受力模型前，首先要按照通用條分法的基本原理對公路土質邊坡進行劃分。再通過構建邊坡受力模型對邊坡的穩定性進行分析[3]。將公路土質邊坡中失去穩定性的滑動體從左到右劃分為m條垂直條，從中選取第x條進行受力分析。圖1為第x條條塊的受力分析圖。

圖1中Ti為第x條條塊的底部切向阻力；Qi為水平方向的地震力；Gi為條塊自身的重量；Ni為條塊底部的有效法向力；Ui為條塊底部的孔隙水壓力；xi-1和xi為條塊左右兩側水平條間力；yi-1和yi為條塊豎直方向上的相互作用力；αi和di分別為條塊的底部坡角和條塊寬。由于滑動部位的面積、形狀已知，因此對條塊進行劃分后，條塊的底長、寬、中心平均高度、底部坡角等參數均可確定。對于整體公路土質邊坡而言，需求解出的未知量為：每條條塊的底部切向力以及有效法向力；相鄰兩個條塊分界面上的法向條間力和切向條間力；條塊兩側法向條間力到公路土質邊坡底部的中心位置距離；公路土質邊坡的安全穩定系數，本文設計的分析方法假設每塊滑體與整個公路土質邊坡的安全穩定系數均相同。

1.2 確定極限平衡分析方程

根據需要確定靜止狀態下，公路土質邊坡的極限平衡分析方程：

第x條條塊底部切向力方向平衡方程：

Ti-(xi-xi-1)cosαi-Qicosαi-(yi-yi-1)sinα=0

(1)

第x條條塊底部有效法向力方向平衡方程：

Ni+Ui+(xi-xi-1)sinαi-(yi-yi-1)cosαi=0

(2)

式(1)，式(2)中各物理量含義與圖1相同。

為了方便后續求解出公路土質邊坡的安全穩定系數，按照常用思維邏輯將假定進行簡化。主要從以下方面進行：

第一，簡化后的假定應滿足公路土質邊坡的力學特征，以及條塊的合理性要求，劃分條塊的側面剪應力不能超過該條塊上表面的最大抗剪強度，即Fv>Fs，其中，Fv為條塊沿垂直方向上的安全穩定系數；Fs為劃分條塊的側面剪應力，此時條塊側面并未達到極限平衡的狀態。

第二，垂直方向上的條塊間沒有相互作用力，邊坡所受作用力的合力，垂直于邊坡內側。根據Tresca屈服準則和Mises屈服準則，邊坡滑動面上的安全穩定系數應為：邊坡抗剪強度指標降低與安全系數相同數值的倍數后，邊坡的滑動面處于極限平衡狀態。

第三，以通用條分法結合邊界約束條件，對邊坡邊界條件的數值進行提取，當條塊寬度到達極限最小值時，邊坡端點兩側作用力的合力與條塊頂點相平行，并確保邊坡滑動面兩端點的外側應力與力矩的取值為0。

以極限平衡方程計算條塊間應力，發現條塊與條塊間的作用力較多，所以，在實際分析過程中，應著眼于作用力相關的量。以Tresca屈服準則和Mises屈服準則作為理論基礎，設邊坡條塊間的切向力與垂直作用力在邊坡滑動面上的法向力具有線性關系。分析邊坡滑動面的實際受力情況，經分析發現，滑動面的受力包括條塊側面的剪切力，以及條塊所受的法向力，二者的力共同作用于邊坡應力圓上，具體的受力分析如圖2所示。

由此可得出土質邊坡中條塊之間的相互作用力存在的關系為：yi=kxi，其中，k為作用力間的系數，為變量，且k的取值在每一條劃分的條塊中的數值均不相同。

1.3 設計數值分析步驟

數據分析具體步驟為：根據公路土質邊坡的具體情況進行分析，選擇對應的最簡方法確定整個邊坡的安全穩定系數的迭代初始數值，從左至右依次進行計算；按照上文確定的平衡公式求解出第二條塊的各項參數數值，再以第二塊條塊為基準，求解出下一條塊的各項參數數值，以此類推直至最右端的條塊數據計算完成。對于公路土質邊坡而言，在分析時需滿足力的平衡，若不滿足，則需要對劃分條塊的側面剪應力進行調整，直至滿足力的平衡要求，獲取相應的曲線關系；將力矩平衡與上文平衡公式結合得出第二條塊的各項參數數值，再以第二條塊作為基準推導出下一條塊，同理得出最右側的側邊值。

2 實驗論證分析

2.1 實驗準備

首先，利用SLIDE仿真軟件構建一個完整的模擬公路土質邊坡，并設定邊坡相應的參數數據：邊坡坡角為23.84°，邊坡坡長1 350 m，邊坡坡寬450 m，邊坡坡高65 m。分別利用兩種穩定性分析方法對該模擬公路土質邊坡的穩定性進行5次分析，設置對照組為傳統穩定性分析方法，實驗組為本文設計的穩定性分析方法。為了確保實驗的準確性，實驗應符合單一變量原則。

2.2 實驗結果及分析

將實驗過程中產生的數據信息：安全穩定系數、分析結果誤差等進行記錄,如表1所示。

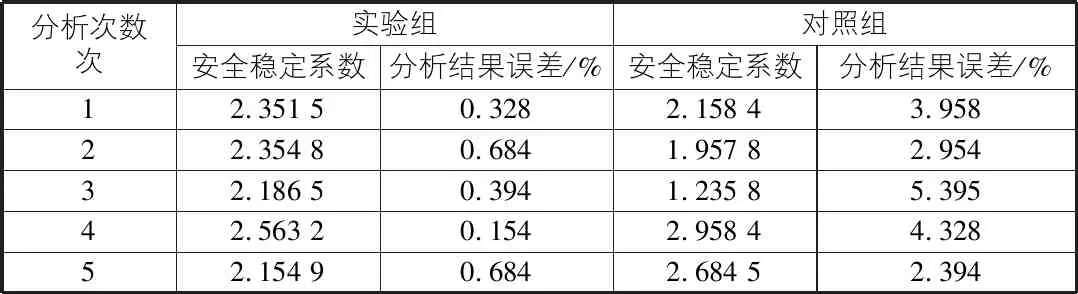
表1 實驗組與對照組實驗結果對比

通過實驗及表1中的數據可知，通過實驗數據可知，實驗組的穩定性分析結果誤差明顯低于對照組，且由表1中第3次分析可以看出，對照組的分析結果誤差大于5%，不符合穩定性分析誤差范圍在5%的要求，而實驗組的分析結果誤差均小于1%。因此，通過實驗證明，本文設計的穩定性分析方法的精準度更高，更適用于實際的應用中。

3 結語

本文通過將極限平衡分析法結合到公路土質邊坡穩定性分析中，通過對比實驗證明了該方法的可行性。但該方法的不足之處在于，只能在設定好的邊坡滑動面上進行分析計算，若對邊坡進行最危險滑動面的搜索需要進行更多的試算，降低了分析方法的效率同時使分析過程更加復雜。因此，在日后的研究中還將對這一方面問題進行更加深入的研究。