基于動力學分析的大重合度直齒圓柱齒輪強度計算

何芝仙，陳 曦，時培成

（安徽工程大學力學重點實驗室，安徽 蕪湖 241000）

圖1 具有縱向重合度的直齒圓柱齒輪示意圖Fig.1 Schematic diagram of spur gear with longitudinal contact-ratio

1 大重合度直齒圓柱齒輪傳動系統(tǒng)的動力學分析

對齒輪傳動系統(tǒng)進行動力學分析，求解作用在輪齒上的動態(tài)法向力的變化規(guī)律，是精確計算齒輪齒根彎曲應力和齒面接觸應力的前提條件［10］。文獻［11］基于單自由度扭轉振動模型，對大重合度直齒圓柱齒輪傳動系統(tǒng)進行了動力學分析。限于篇幅，本文不再贅述分析過程，直接給出大重合度直齒圓柱齒輪輪齒間動態(tài)法向力的計算結果。設置大重合度直齒圓柱齒輪的參數(shù)：齒數(shù)z1=41，z2=60，模數(shù)m=5 mm，單排齒輪的齒寬b=40.5 mm，小齒輪的轉速n1=960 r/min，傳遞功率P=50 kW。

圖2為相同工況下漸開線標準直齒圓柱齒輪和大重合度直齒圓柱齒輪的單對輪齒間動態(tài)法向力的變化規(guī)律。由圖2可知，大重合度直齒圓柱齒輪傳動的重合度較大，動態(tài)法向力由錯開半個齒距的雙排齒輪共同承擔，與相同工況下的漸開線標準直齒圓柱齒輪相比，其單對輪齒所承受的最大動態(tài)法向力由3 709.5 N減小為2 324.2 N，減小了37.34%。大重合度直齒圓柱齒輪的總動態(tài)法向力通過排間分配和齒間分配的方式分配到每對嚙合的輪齒上，分別如圖3和圖4所示。圖5所示為大重合度直齒圓柱齒輪嚙合過程中前排齒輪單對輪齒間的法向力變化曲線，由圖可見，相比于靜態(tài)法向力峰值，動態(tài)法向力峰值顯著增大，其由1 856.1 N增大為2 324.2 N，增大了25.22%，這是由齒輪傳動系統(tǒng)的動力學效應引起的。因此，分析作用在齒輪輪齒間的動態(tài)法向力是計算齒輪強度的前提條件。

圖2 直齒圓柱齒輪單對輪齒間的動態(tài)法向力Fig.2 Dynamic normal force between a pair of teeth of spur gear

圖3 大重合度直齒圓柱齒輪的總動態(tài)法向力及其排間分配Fig.3 Total dynamic normal force and its distribution between rows of spur gear with high contact-ratio

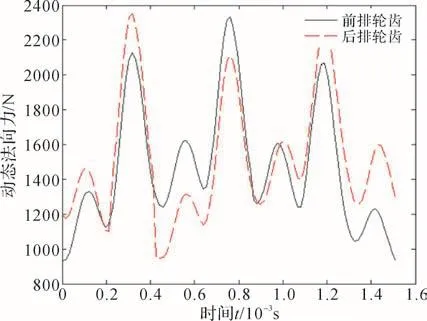
圖4 大重合度直齒圓柱齒輪動態(tài)法向力的齒間分配Fig.4 Distribution of dynamic normal force between teeth of spur gear with high contact-ratio

圖5 大重合度直齒圓柱齒輪前排齒輪單對輪齒間的法向力Fig.5 Normal force between a pair of teeth of front row gear of spur gear with high contact-ratio

2 大重合度直齒圓柱齒輪的齒根彎曲應力計算

計算齒根彎曲應力和齒面接觸應力是齒輪強度分析的關鍵內容。ISO 6336-6—2006［12-13］中漸開線標準直齒圓柱齒輪齒根彎曲應力的計算方法是以材料力學理論為基礎的，其對齒輪傳動系統(tǒng)動力學效應對齒根彎曲應力的影響處理得比較粗糙，計算結果偏于保守。隨著計算機技術的發(fā)展，彈性力學有限元分析法已經成為計算齒輪齒根彎曲應力的有效方法［12-15］，但在計算齒根彎曲應力時考慮齒輪傳動系統(tǒng)動力學效應的相關研究仍很少見。

在已知大重合度直齒圓柱齒輪幾何材料參數(shù)以及其輪齒間法向力的條件下，利用ANSYS軟件中的APDL（ANSYS parametric design language，ANSYS參數(shù)化設計語言）進行參數(shù)化編程，以實現(xiàn)其齒根彎曲應力的計算，具體計算流程（見圖6）如下。

步驟1：參數(shù)設置。輸入大重合度直齒圓柱齒輪的幾何物理參數(shù)并建立幾何模型，將齒面從開始嚙合到退出嚙合的過程分成N份，設置計算次數(shù)N，令k=1。

步驟2：網格劃分和設置邊界條件。選擇ANSYS軟件中形狀逼近功能強的Plane 82單元，對大重合度直齒圓柱齒輪的幾何模型進行網格劃分，其單個輪齒的有限元模型如圖7所示。設置位移邊界條件：選擇約束底邊節(jié)點2個方向的自由度，即ux=0，uy=0；約束兩側邊x方向的自由度，即ux=0。

步驟3：齒根彎曲應力計算。從齒頂?shù)烬X根動態(tài)地施加法向力，每向1個嚙合點位置施加法向力就進行一次有限元分析，求解危險點的彎曲應力并記錄。

圖6 大重合度直齒圓柱齒輪齒根彎曲應力計算流程Fig.6 Computational flow of tooth root bending stress of spur gear with high contact-ratio

圖7 大重合度直齒圓柱齒輪單個輪齒的有限元模型Fig.7 Finite element model of single tooth of spur gear with high contact-ratio

由于所選擇的大重合度直齒圓柱齒輪前后2排齒輪僅相差半個齒距，其齒根彎曲應力以及齒面接觸應力的變化也僅相差半個齒距對應的嚙合時間，限于篇幅，僅給出前排齒輪的計算結果。圖8所示為在分別施加動態(tài)法向力和靜態(tài)法向力的情況下大重合度直齒圓柱齒輪嚙合過程中前排齒輪齒根彎曲應力的變化曲線。此處的彎曲應力是基于第三強度理論計算的等效應力，嚙合點位置x=0 mm對應的是實際嚙合的起始點。由圖8可知，大重合度直齒圓柱齒輪前排齒輪的齒根彎曲應力變化十分復雜，與作用在輪齒上的法向力以及嚙合點位置密切相關。當法向力作用在輪齒齒頂時，其齒根彎曲應力并非最大。結合圖5和圖8可知，當法向力在齒頂附近出現(xiàn)第1個峰值時，齒根彎曲應力取得最大值。與施加靜態(tài)法向力時的計算結果相比，考慮齒輪傳動系統(tǒng)動力學效應時，前排齒輪的齒根彎曲應力變化曲線較為光滑，且齒根彎曲應力較大，最大齒根彎曲應力由118.12 MPa增大到144.68 MPa，增大了22.49%。這說明齒輪傳動系統(tǒng)動力學效應對齒根彎曲應力的影響十分顯著，且這僅僅還是齒輪傳動系統(tǒng)內部參數(shù)激振引起的。與相同工況下漸開線標準直齒圓柱齒輪相比（見圖9），大重合度直齒圓柱齒輪前排齒輪的最大齒根彎曲應力由174.49 MPa減小為144.68 MPa，減小了17.08%。由此可知，本文討論的大重合度直齒圓柱齒輪的齒根彎曲強度顯著提高。

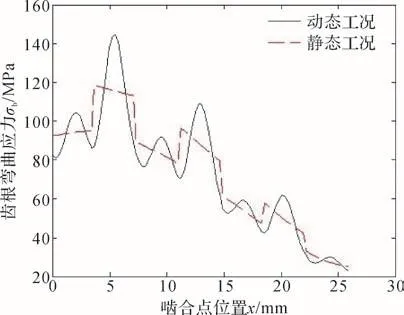
圖8 大重合度直齒圓柱齒輪前排齒輪的齒根彎曲應力變化曲線Fig.8 Variation curve of tooth root bending stress of front row gear of spur gear with high contact-ratio

3 大重合度直齒圓柱齒輪的齒面接觸應力計算

采用Hertz公式計算齒輪的齒面接觸應力較為方便且計算精度較高，其與有限元分析法的相對誤差在0.66%以內［16］。齒輪齒面接觸應力的計算公式為［17-20］：

圖9 漸開線標準直齒圓柱齒輪的齒根彎曲應力變化曲線Fig.9 Variation curve of tooth root bending stress of involute standard spur gear

與漸開線標準直齒圓柱齒輪不同，大重合度直齒圓柱齒輪齒面接觸應力的大小主要取決于嚙合點處綜合曲率半徑和輪齒間法向力的大小。對于本文討論的大重合度直齒圓柱齒輪，法向力不由1對輪齒承擔，其齒面接觸應力的最大值一般不出現(xiàn)在節(jié)圓附近［17］。基于上文分析得到的大重合度直齒圓柱齒輪前排齒輪輪齒間的法向力，利用式（1）計算其前排齒輪的齒面接觸應力（從齒頂?shù)烬X根），結果如圖10所示。由圖10可知，大重合度直齒圓柱齒輪前排齒輪的齒面接觸應力與輪齒間法向力的變化規(guī)律十分相似，但最大齒面接觸應力出現(xiàn)在法向力取得次峰值時所對應的嚙合點位置（x=5.484 1 mm）處，這是因為該位置處輪齒間的法向力較大且綜合曲率半徑較小。與靜態(tài)工況相比，考慮齒輪傳動系統(tǒng)動力學效應時大重合度直齒圓柱齒輪前排齒輪的最大齒面接觸應力由197.6 MPa增大為219.22 MPa，增大了10.94%。但與同樣工況下的漸開線標準直齒圓柱齒輪相比（見圖11），其最大齒面接觸應力由390.03 MPa減小為219.22 MPa，減小了43.79%。由此可知，本文討論的大重合度直齒圓柱齒輪的齒面接觸強度也有較大幅度的提高。

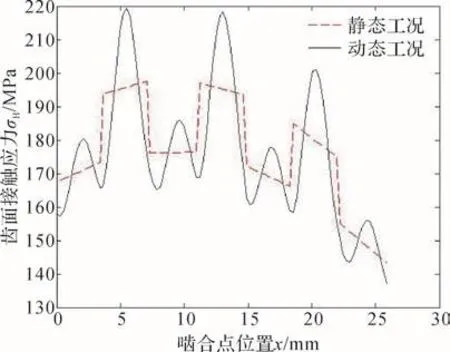
圖10 大重合度直齒圓柱齒輪前排齒輪的齒面接觸應力變化曲線Fig.10 Variation curve of tooth surface contact stress of front row gear of spur gear with high contact-ratio

圖11 漸開線標準直齒圓柱齒輪的齒面接觸應力變化曲線Fig.11 Variation curve of tooth surface contact stress of involute standard spur gear

4 結論

1）與相同工況下的漸開線標準直齒圓柱齒輪相比，大重合度直齒圓柱齒輪在性能上具有以下獨特的優(yōu)勢：

①大重合度直齒圓柱齒輪單對輪齒所承受的最大動態(tài)法向力減小了37.34%。

②大重合度直齒圓柱齒輪的最大齒根彎曲應力減小了17.08%，且并不在法向力作用在齒頂處時出現(xiàn)；最大齒面接觸應力減小了43.79%，且不出現(xiàn)在節(jié)圓附近。

2）與靜態(tài)工況相比，考慮齒輪傳動系統(tǒng)動力學效應時，大重合度直齒圓柱齒輪的最大齒根彎曲應力增大了22.49%，最大齒面接觸應力增大了10.94%，說明齒輪傳動系統(tǒng)動力學效應對齒輪的齒根彎曲強度和齒面接觸強度的影響顯著。

綜上，大重合度直齒圓柱齒輪在保留漸開線標準直齒圓柱齒輪優(yōu)點的前提下，其動力學性能和承載能力均明顯改善，應用潛力巨大。