變參數下角接觸球軸承保持架的穩定性與振動特性分析
曾 光,邊 強,趙春江,殷玉楓,馮毅杰
(1.太原科技大學機械工程學院,山西 太原 030024;2.太原科技大學重型機械教育部工程研究中心,山西 太原 030024)
保持架是角接觸球軸承的重要元件之一,用于均勻地隔離滾珠和引導滾珠保持在滾道內。引導間隙和兜孔間隙是保持架的重要結構參數,其直接影響保持架的受力和性能。保持架間隙參數設計不合理會增大保持架與滾珠、引導套圈間的碰撞力和摩擦力,導致軸承運動失穩,嚴重時會引起保持架斷裂或軸承磨損等故障。在保持架設計前期,通過振動分析來預測其動態性能,可避免共振的發生;通過優化引導間隙和兜孔間隙等參數可使保持架具有更好的防振性能。因此,針對不同引導間隙和兜孔間隙下保持架穩定性和振動特性的研究具有實際工程意義。
對于高速角接觸球軸承的動態性能分析,國外的Jones[1]提出了套圈滾道控制理論,解決了滾動軸承的動力學分析問題;Harris[2]結合彈流潤滑理論建立了第1種高速球軸承擬靜力學分析方法,但未分析保持架的動態特性;Gupta[3]利用理論分析與試驗相結合的方法研究發現,在一定工況條件下,保持架的引導間隙和兜孔間隙對其穩定性有直接影響。國內的鄧四二等[4]采用柔體動力學分析方法,研究了保持架的動態性能,并對基于柔體動力學和剛體動力學的保持架動態性能進行了對比分析;張剛等[5]利用ANSYS/LS-DYNA對特定工況下的滾動軸承進行了顯式動力學仿真分析,得到了滾珠的應力、加速度和位移等的變化規律;馮勁輝等[6]使用ABAQUS-Explicit顯式算法對軸承進行了動力學分析;葉振環等[7]利用擬動力學方法建立了以保持架的引導方式和兜孔間隙為設計變量的優化模型,并提出了相應的優化方案;劉秀海[8]建立了考慮碰撞等因素的高速滾動軸承動力學模型,并研究了載荷、轉速、游隙和間隙比等對其保持架穩定性的影響。上述文獻均對角接觸球軸承的特性進行了分析,且部分文獻還研究了保持器結構參數對軸承動態特性的影響,但仍缺乏對引導間隙和兜孔間隙等結構參數對保持架振動特性影響的研究。保持架的固有頻率過小會引發保持架共振,從而縮短保持架的使用壽命。因此,在設計保持架結構參數時,需同時考慮保持架的穩定性和振動特性。
為此,筆者綜合考慮角接觸球軸承各元件間的動態接觸和變形關系,借助ABAQUS軟件建立7005型角接觸球軸承的顯式動力學模型,求解不同引導間隙和兜孔間隙下保持架的打滑率、質心渦動速度偏差比和各階振動模態的固有頻率,同時對不同引導間隙和兜孔間隙下保持架的穩定性和振動特性進行分析,旨在為保持架的優化設計提供理論依據。
1 保持架穩定性與振動特性的理論分析
1.1 保持架穩定性的理論分析
保持架的穩定性可通過打滑率和質心渦動速度偏差比來判斷[9-10]。保持架的打滑率定義為保持架的理論轉速與實際轉速之間的誤差。其中,保持架的理論轉速可根據角接觸球軸承的運動學關系(見圖1)計算得到,實際轉速可從角接觸球軸承顯式動力學模型中直接提取。
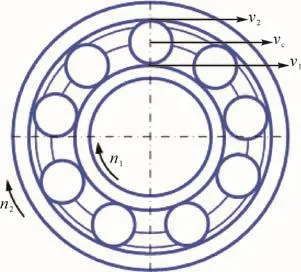
圖1 角接觸球軸承運動學關系示意圖Fig.1 Schematic diagram of kinematics relationship of angular contact ball bearing
假設角接觸球軸承的內、外圈同時轉動,滾珠與軸承內、外圈的接觸角α相同,由此可得滾珠與軸承內、外圈的接觸點的線速度v1、v2為:
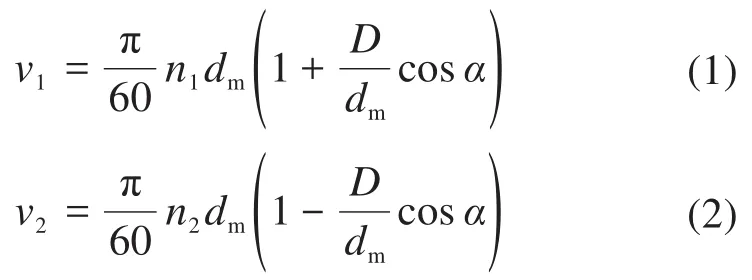
式中:n1、n2分別為軸承內、外圈的轉速;dm為節圓直徑;D為滾珠直徑。
假設保持架的角速度與滾珠公轉的角速度相等,則滾珠質心的線速度為其與軸承內、外圈接觸點的線速度的平均值,由此可得保持架的線速度vc為:
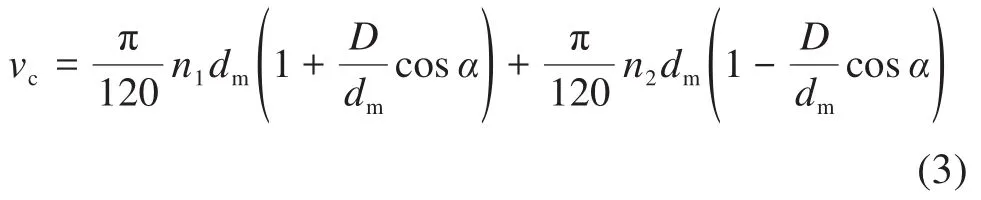
保持架的線速度vc還可表示為:
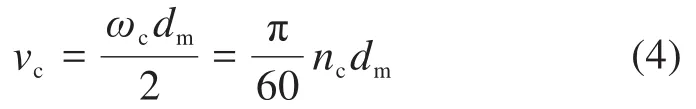
式中:ωc為保持架的角速度;nc為保持架的轉速。
軸承內、外圈的角速度與轉速之間的關系為:
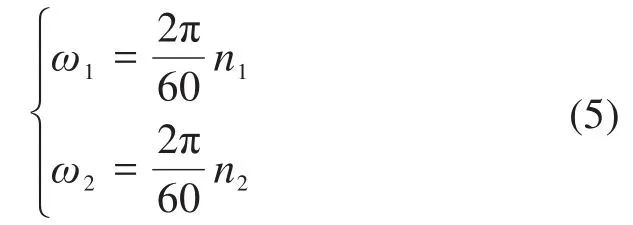
式中:ω1、ω2分別為軸承內、外圈的角速度。
聯立式(3)至式(5),得到保持架的理論角速度為:
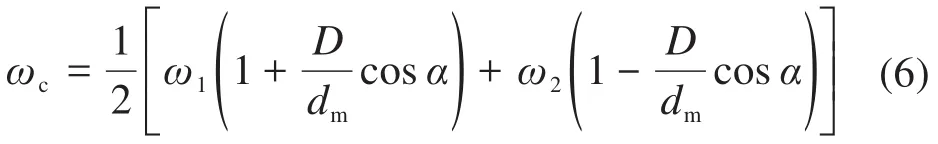
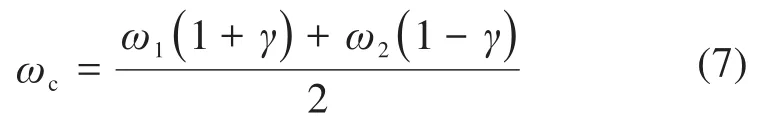
則保持架的打滑率S為:
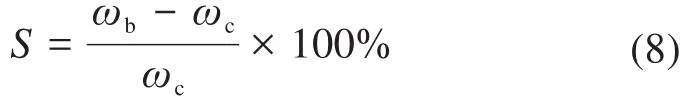
式中:ωb為保持架的實際角速度。
保持架的質心渦動速度偏差比定義為保持架質心瞬時線速度的標準偏差與其平均線速度的比值。質心渦動速度偏差比越小表示保持架的穩定性越好,其計算公式為:
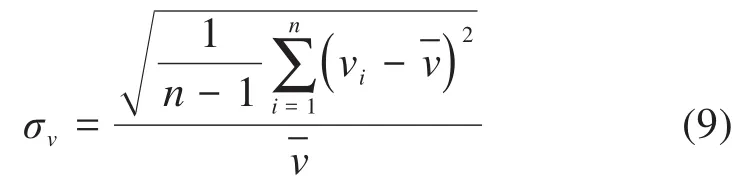
式中:v(ii=1,2,…,n)為各時刻保持架質心的線速度;為保持架質心的平均線速度。
1.2 保持架振動特性的理論分析
模態分析是動力學分析的基礎,振動模態可以反映機構的固有振動性能[12]。通過對角接觸球軸承保持架的模態振型和各階振動模態的固有頻率進行分析,可以預測保持架在實際運動過程中的振動響應,從而有效地避免共振。
具有h個自由度的線性系統的振動方程為:
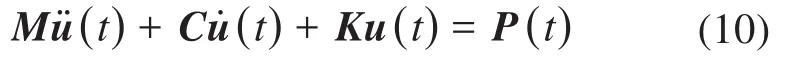
式中:M為系統的質量矩陣;C為系統的阻尼矩陣;K為系統的剛度矩陣;u(t)為系統的位移向量;u?(t)為系統的速度向量;u?(t)為系統的加速度向量;P(t)為系統的載荷向量。
在不考慮系統阻尼和外力的情況下,線性系統的自由振動方程為:
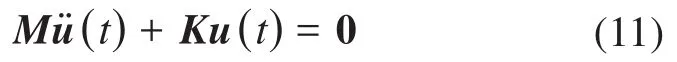
式(11)的通解為:
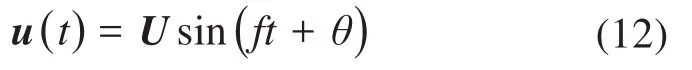
式中:U為系統的位移幅值向量;θ為系統的初相位;f為系統的固有頻率。
將式(12)代入式(10),可得該線性系統位移的齊次方程,為:
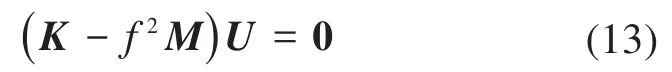
令式(13)中U的系數為0,可得到齊次方程的非零解,即:

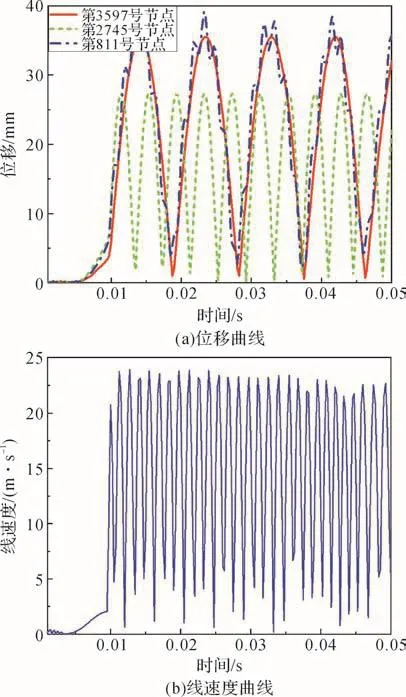
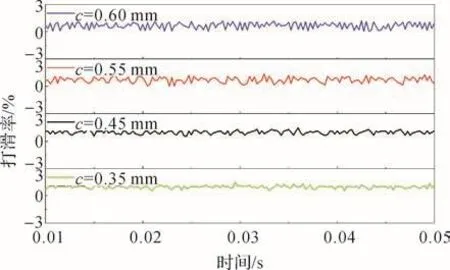
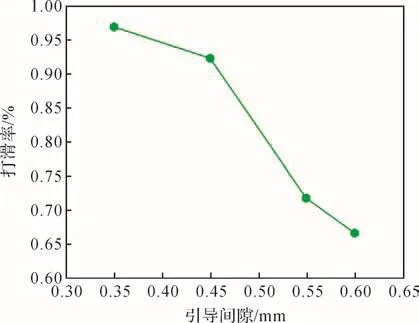
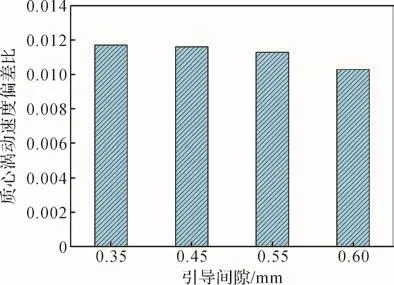
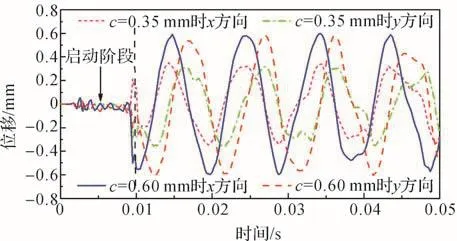
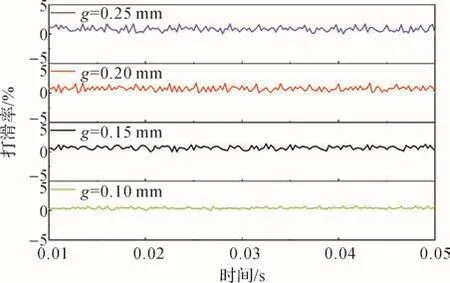
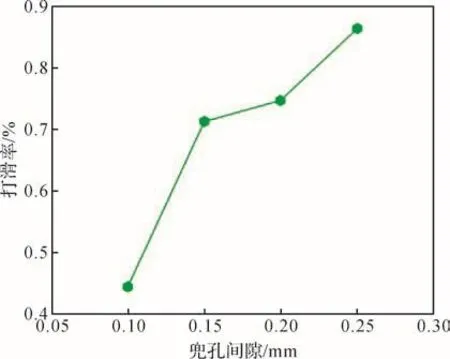
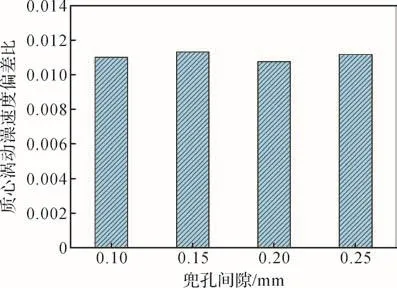
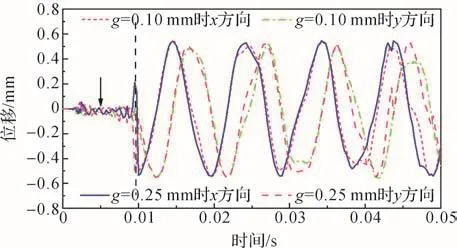
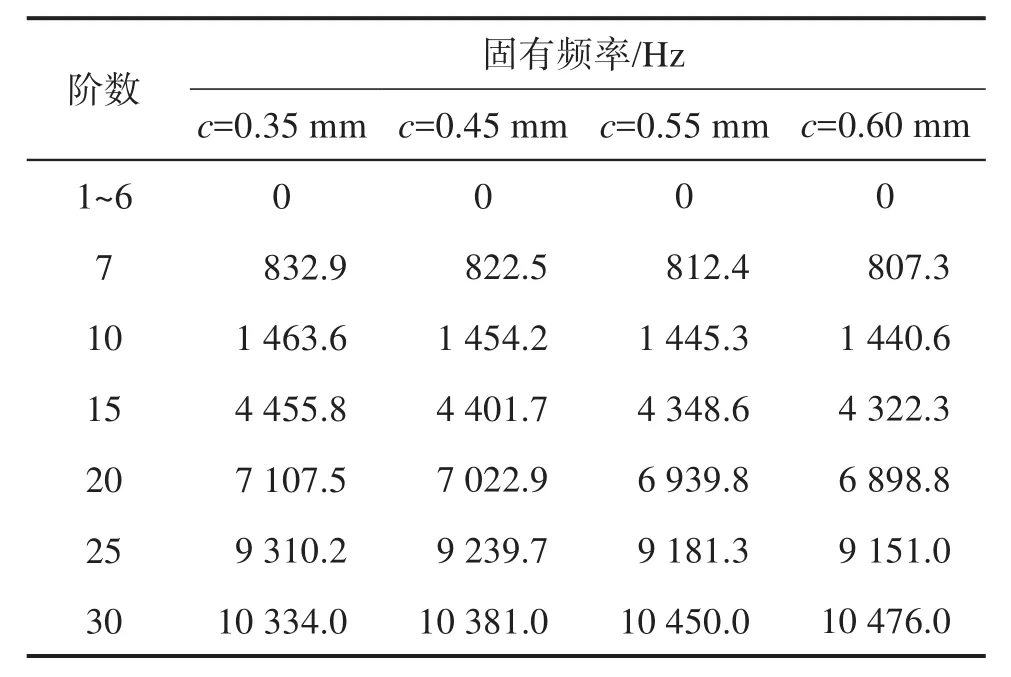
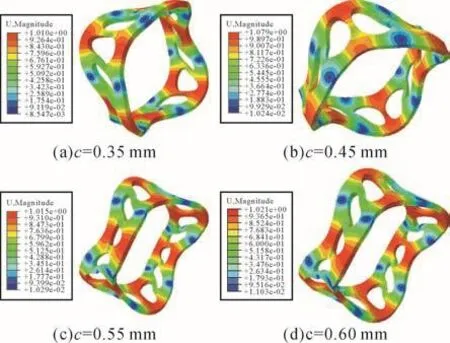
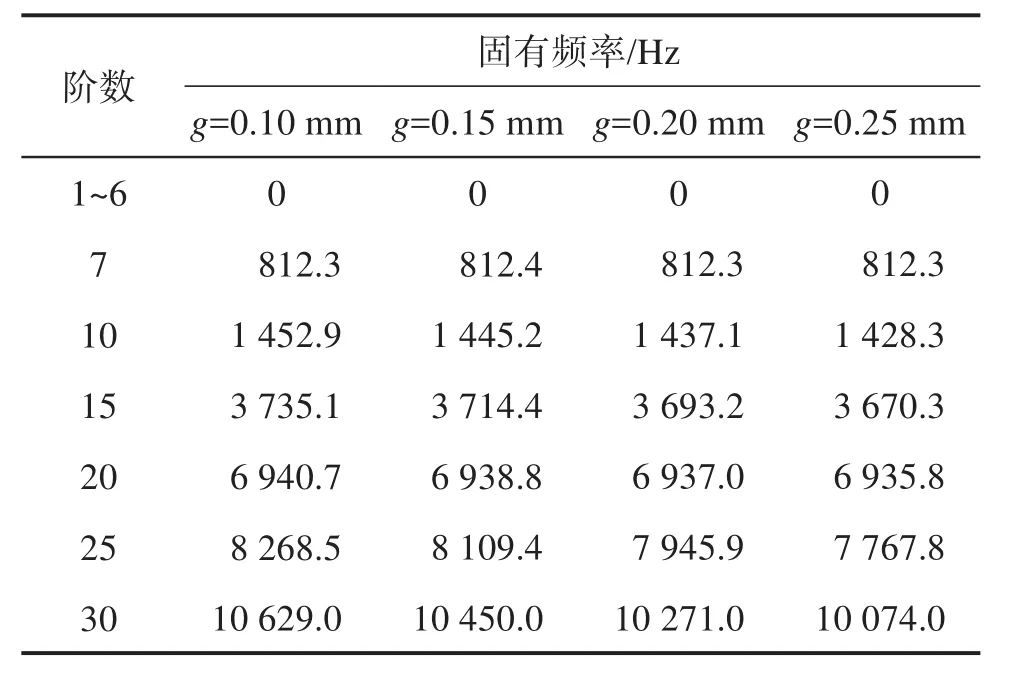
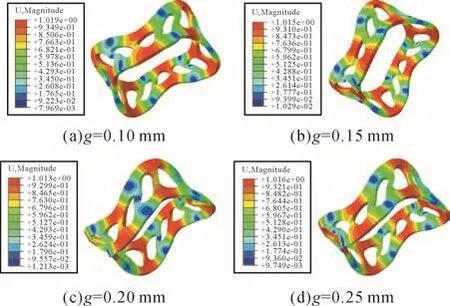
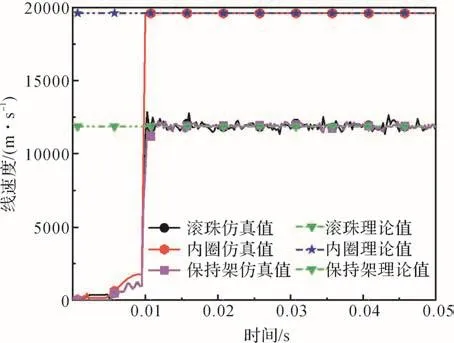
將式(14)展開后可得關于f2的h次方程。若M和K均為正定矩陣,則可求出頻率方程的h個特征值,表示為f2j(j=1,2,…,h),各個特征值的平方根即為該線性振動系統的固有頻率fj,且f1 令ψj表示對應f2j的振型向量,代入式(13)可得: 求解式(15)即可得到線性振動系統的模態向量。對于齊次方程(13),其有無數個解,即任意常數倍的ψj均為該齊次方程的解。假設任意常數為a,則有Uj=aψj。此時模態向量ψj中元素間的相對比值保持不變,說明模態振型是唯一的[13]。 ABAQUS-Explicit是一種高效的復雜非線性數值問題求解工具。軸承的動態接觸問題即為復雜的非線性問題,且軸承的材料、各元件之間的動態接觸關系及其所受載荷的影響增大了計算難度。借助ABAQUS-Explicit可以很便捷地分析軸承的動態接觸關系[5]。 在t時刻的增量步開始時,計算得到的節點加速度為: 采用中心差分法對節點的加速度進行積分計算。在計算節點的速度時,假設其加速度為常數,t時刻增量步中間時刻的節點速度為: 式中:Δt為增量步步長。 同樣,在計算節點的位移時,假設其速度為常數,則t時刻增量步末節點的位移為: 得到節點的位移后,通過應變速率和本構關系獲得節點的應力矩陣[14-15]。 本文以7005型角接觸球軸承為研究對象,其基本結構參數如表1所示。 表1 7005型角接觸球軸承的基本結構參數Table 1 Basic structural parameters of 7005 type angular contact ball bearing 根據表1中的參數,在SolidWorks軟件中建立7005型角接觸球軸承的三維實體模型,并將其導入ABAQUS軟件。在ABAQUS軟件的屬性單元中,設置軸承內、外圈的材料為軸承鋼,彈性模量為 2.0×105MPa,密度為7 800 kg/m3,泊松比為 0.3;保持架的材料為尼龍,彈性模量為2 600 MPa,密度為1 240 kg/m3,泊松比為0.35;滾珠的材料為氮化硅,彈性模量為3.2×105MPa,密度為3 200 kg/m3,泊松比為0.26;各元件截面均為均質實體。 當7005型角接觸球軸承工作時,其滾珠與保持架及內、外圈之間的接觸和運動關系非常復雜;同時,滾珠和保持架之間的相互撞擊會導致保持架與內圈的轉動不同步。因此,為了盡可能真實地模擬角接觸球軸承各元件之間的動力學關系,在建模時將滾珠、保持架及內、外圈視為彈性體。建立內、外圈滾道表面與滾珠的接觸,保持架內、外表面與內圈外表面和外圈內表面的接觸,以及滾珠與保持架兜孔的接觸,共建立44對接觸對。設置接觸類型為表面與表面接觸,接觸屬性中切向接觸公式選罰接觸,保持架與滾珠及引導面間的摩擦因數為0.1,內、外圈滾道表面與滾珠間的摩擦因數為0.05,滑移公式為有限滑移公式,法向接觸為硬接觸,允許接觸后分離。在設置邊界條件和施加載荷時,將角接觸球軸承外圈固定,并對其內圈施加載荷與轉速,利用內圈帶動滾珠和保持架轉動;設置仿真時間為0.05 s。 在對7005型角接觸球軸承三維實體模型進行網格劃分時,將其各元件拆分后再進行網格劃分。采用以六面體為主的掃掠方式對保持架進行網格劃分,采用六面體掃掠方式對其余元件進行網格劃分;為了保證計算精度,對內、外圈滾道的表面及保持架的兜孔表面進行網格細化。設定六面體單元的類型為C3D8R,楔形塊單元的類型為C3D6R。7005型角接觸球軸承的有限元模型如圖2所示。 圖2 7005型角接觸球軸承的有限元模型Fig.2 Finite element model of 7005 type angular contact ball bearing 當施加在7005型角接觸球軸承內圈上的軸向載荷Fa=2 000 N,徑向載荷Fr=200 N,轉速n1=15 000 r/min時,該軸承部分節點的動態響應曲線如圖3所示。其中:第3597號節點位于保持架外表面,第2745號節點位于滾珠與軸承內圈接觸處,第811號節點位于滾珠與軸承外圈接觸處。圖3(a)為所選取的3個節點的位移曲線;圖3(b)為第811號節點的線速度曲線。 圖3 7005型角接觸球軸承部分節點的動態響應曲線Fig.3 Dynamic response curves of some nodes of 7005 type angular contact ball bearing 從圖3(a)中可以看出,滾珠與保持架的運動均具有周期性。從圖3(b)中可以看出,在0.007 s時滾珠的線速度開始逐漸增大,說明此時軸承內圈開始轉動,滾珠在軸承內圈的帶動下開始轉動。在該線速度曲線上,波谷表示滾珠與軸承外圈接觸時的線速度,波峰表示滾珠與軸承內圈接觸時的線速度。滾珠的轉動周期為0.001 4 s,其與軸承內圈接觸時的平均線速度為23.054 m/s。 2.3.1 引導間隙對保持架穩定性的影響 在7005型角接觸球軸承內圈上軸向載荷Fa=2 000 N,徑向載荷Fr=200 N,轉速n1=15 000 r/min,兜孔間隙g=0.15 mm的工況下,取引導間隙c=0.35,0.45,0.55,0.60 mm,分析不同引導間隙下保持架的打滑率和質心渦動速度偏差比,結果如圖4、圖5和圖6所示。 圖4 不同引導間隙下保持架打滑率隨時間的變化曲線Fig.4 Variation curve of cage slip rate with time under different guide clearances 圖5 不同引導間隙下保持架的打滑率均值Fig.5 Average slip rate of cage under different guide clearances 圖6 不同引導間隙下保持架的質心渦動速度偏差比Fig.6 Deviation ratio of centroid whirl velocity of cage under different guide clearances 由圖4和圖5可以看出,隨著引導間隙的增大,保持架的打滑率均值逐漸減小,表明其穩定性逐漸增強,這與文獻[7]所得的軸承內圈引導時保持架穩定性的變化規律一致。但隨著引導間隙的增大,保持架打滑率的波動幅度逐漸增大,這是因為當引導間隙增大時,保持架的徑向運動空間隨之擴大。由圖6可知,當引導間隙增大時,保持架的質心渦動速度偏差比逐漸減小,但變化不明顯,這是因為當引導間隙比較小時,軸承內、外圈與保持架之間很容易發生碰撞,導致保持架難以保持平穩。因此,適當增大保持架引導間隙可以提高其穩定性,但是從整體上看,引導間隙對保持架穩定性的影響并不大。 圖7為引導間隙c=0.35和0.60 mm時保持架質心位移的變化曲線。從圖7中可以看出,隨著引導間隙的增大,保持架質心的最大位移增大,且位移的變化更加具有規則性,說明增大引導間隙可使保持架的穩定性增強。另外,在啟動階段,保持架質心在x與y方向上的位移變化不具有周期性;在平穩運行階段,保持架質心在x與y方向上的位移變化具有較強的周期性。 圖7 不同引導間隙下保持架質心位移的變化曲線Fig.7 Variation curve of displacement of cage centroid under different guide clearances 2.3.2 兜孔間隙對保持架穩定性的影響 在7005型角接觸球軸承內圈上的軸向載荷Fa=2 000 N,徑向載荷Fr=200 N,轉速n1=15 000 r/min,引導間隙c=0.55 mm的工況下,取兜孔間隙g=0.10,0.15,0.20,0.25 mm,分析不同兜孔間隙下保持架的打滑率和質心渦動速度偏差比,結果如圖8、圖9和圖10所示。 圖8 不同兜孔間隙下保持架打滑率隨時間的變化曲線Fig.8 Variation curve of cage slip rate with time under different pocket clearances 由圖8和圖9可以看出,隨著兜孔間隙的增大,保持架打滑率的波動幅度和均值逐漸增大。這說明適當減小兜孔間隙有利于減少保持架滑動,提高保持架的穩定性。由圖10可知,保持架的質心渦動速度偏差比總體上變化不大且無明顯規律,這與文獻[16]所得結果相符。但是,當保持架兜孔間隙過小時,在軸承運動過程中兜孔與滾珠間會頻繁接觸和碰撞,導致保持架與滾珠間相互作用,不利于保持架的穩定運動,因此保持架的兜孔間隙不宜過小。 圖9 不同兜孔間隙下保持架的打滑率均值Fig.9 Average slip rate of cage under different pocket clearances 圖10 不同兜孔間隙下保持架的質心渦動速度偏差比Fig.10 Deviation ratio of centroid whirl velocity of cage under different pocket clearances 圖11為兜孔間隙g=0.10和0.25 mm時保持架質心位移的變化曲線。從圖11中可以看出,兜孔間隙的變化對保持架質心位移的影響較小。 圖11 不同兜孔間隙下保持架質心位移的變化曲線Fig.11 Variation curve of displacement of cage centroid under different pocket clearances 將保持架三維實體模型導入ABAQUS軟件,并對其賦予材料屬性,具體參數如表1所示。然后,對保持架三維實體模型進行網格劃分,仍采取以六面體為主的掃掠方式。由于要求解保持架的高階振動模態,而高階振動模態下保持架的變形較大,為了保證計算精度,對保持架有限元模型進行網格細化。采用Lanczos快速求解特征器進行求解[17],提取保持架前30階振動模態。 3.2.1 引導間隙對保持架振動模態的影響 當7005型角接觸球軸承保持架的兜孔間隙g=0.15 mm時,不同引導間隙下保持架前30階振動模態的固有頻率如表2所示。由表2可知,自由狀態下保持架前6階振動模態為剛性模態,其固有頻率均為0 Hz。基于轉速與頻率間的關系,計算保持架各階振動模態對應的極限轉速,確保保持架轉速不超過極限轉速的75%,就可以避免共振[18]。從表2中還可以看出,保持架前30階(除前6階外)振動模態的最小固有頻率為807.3 Hz,其對應的臨界轉速為36 329.4 r/min,而本文設置的軸承內圈的轉速為15 000 r/min,顯然不會發生共振。另外,保持架前25階(除前6階外)振動模態的固有頻率均隨引導間隙的增大而減小,說明引導間隙越大,保持架越容易發生共振。 表2 不同引導間隙下保持架各階振動模態的固有頻率Table 2 Natural frequency of each order vibration mode of cage under different guide clearances 圖12為不同引導間隙下保持架第30階模態的振型。從圖12中可以看出,當引導間隙c=0.35mm時,保持架兩兜孔中間部位的變形最嚴重;隨著引導間隙的增大,兜孔左右兩側部位的變形量增大。 圖12 不同引導間隙下保持架第30階模態的振型Fig.12 Vibration shape of 30th order mode of cage under different guide clearances 3.2.2 兜孔間隙對保持架振動模態的影響 當7005型角接觸球軸承保持架的引導間隙c=0.55 mm時,不同兜孔間隙下保持架前30階振動模態的固有頻率如表3所示。從表3中可以看出,保持架前6階振動模態的固有頻率為0 Hz,此時保持架為剛體振動。保持架各階(除前6階外)振動模態的固有頻率隨兜孔間隙的增大而減小,說明兜孔間隙越大,保持架越容易發生共振,因此兜孔間隙不宜過大。 表3 不同兜孔間隙下保持架各階振動模態的固有頻率Table 3 Natural frequency of each order vibration mode of cage under different pocket clearances 圖13為不同兜孔間隙下保持架第30階模態的振型。從圖13中可以看出,保持架變形最大的位置為兜孔左右兩側部位。 在7005型角接觸球軸承內圈上的軸向載荷Fa=2 000 N,徑向載荷Fr=200 N,轉速n1=15 000 r/min的工況下,該軸承各元件線速度的仿真值與理論值對比如圖14所示。從圖14中可以看出,角接觸球軸承內圈在0.007 s后開始加速并帶動保持架與滾珠一起轉動。在0.01 s后,角接觸球軸承各元件的轉動達到平穩狀態。圖14結果表明,角接觸球軸承保持架線速度的仿真值略高于理論值,相對誤差為0.099 6%;軸承內圈和滾珠的線速度的仿真值均略低于理論值,相對誤差分別為0.086 0%和0.030 0%。有限元仿真分析得到的線速度的波動不大,且與理論值基本吻合,這在一定程度上驗證了所建立的角接觸球軸承顯式動力學模型的準確性。 圖13 不同兜孔間隙下保持架第30階模態的振型Fig.13 Vibration shape of 30th order mode of cage under different pocket clearances 圖14 7005型角接觸球軸承各元件線速度的變化曲線Fig.14 Variation curve of linear velocity of each component of 7005 type angular contact ball bearing 本文利用ABAQUS軟件建立了7005型角接觸球軸承的顯式動力學模型,分析了引導間隙和兜孔間隙對保持架穩定性及振動特性的影響,得出以下結論。 1)隨著引導間隙的增大,保持架的打滑率、質心渦動速度偏差比和各階振動模態的固有頻率均減小,保持架的穩定性增強,但共振風險增大。 2)隨著兜孔間隙的增大,保持架的打滑率增大,質心渦動速度偏差比變化不明顯,各階振動模態的固有頻率減小,保持架的穩定性減弱,共振風險增大。 研究得到的變參數下保持架的穩定性和振動特性分析結果可為高速角接觸球軸承保持架的優化設計提供理論依據。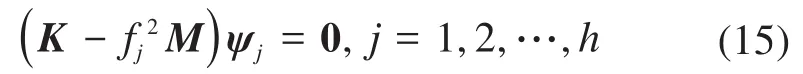
2 基于ABAQUS-Explicit的變參數下保持架的穩定性分析
2.1 ABAQUS-Explicit的計算原理
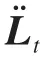

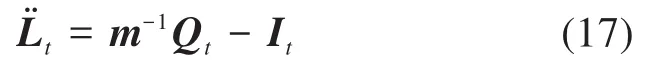
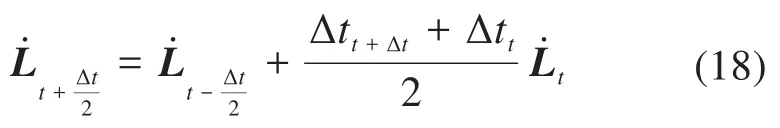
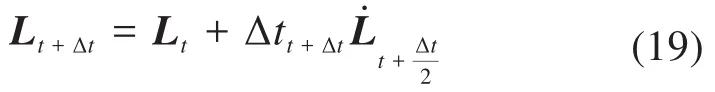
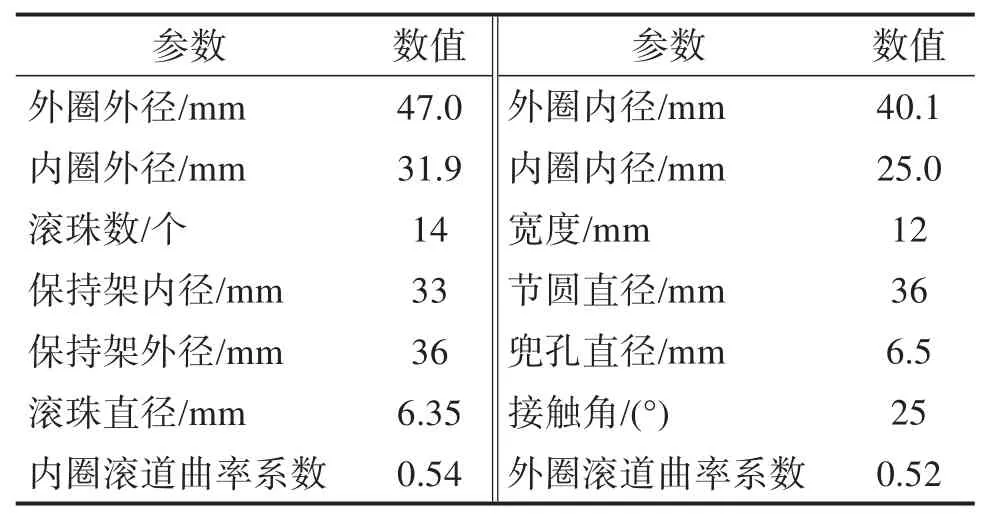
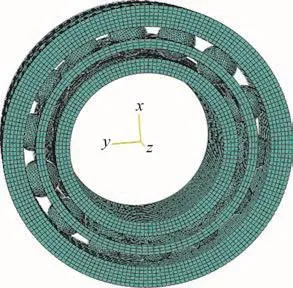
2.2 有限元模型建立
2.3 計算結果與分析
3 變參數下保持架的振動特性分析
3.1 保持架振動模態分析模型建立
3.2 保持架振動模態分析
4 顯示動力學模型的準確性驗證
5 結論

