運用含復雜網絡結構的多種群遺傳算法求解FJSP

石宇強，田永政，張雨琦，石小秋

西南科技大學 制造科學與工程學院，四川 綿陽621000

遺傳算法[1]（Genetic Algorithm，GA）是歷史上備受關注的進化算法之一。標準GA 在求解組合優化等問題上具有獨特的優勢，但是極易早熟收斂。為了克服這一缺點，多種群遺傳算法（Multi-population Genetic Algorithm，MGA）隨之出現，并獲得了廣泛的關注和應用[2-4]。MGA將標準GA的單種群劃分為多個子群，保證了種群的多樣性，每個子群內的個體按照標準GA 進化，精英個體在子群間遷徙傳播優勢基因，從而避免早熟收斂[5-6]。如文獻[2]利用MGA 實現非線性動力學模型參數的辨識，預測橡膠波形發生器產生的沖擊脈沖。文獻[3]采用MGA 對常用的多孔吸聲結構參數進行優化。但是，傳統MGA的子群數有限，且大多忽略了子群結構對算法性能的影響。如果把子群以及它們之間的交流（優勢基因的傳播）分別看作節點和邊，那么MGA就是一個復雜網絡，代表了不同子群間的相互作用關系[7-8]。以往研究表明，復雜網絡的集體行為會受到網絡結構的顯著影響[9-13]。類似地，MGA中子群間的交流構成的網絡結構也將影響其尋優行為，進而影響MGA 的性能。

復雜網絡可以描述自然界和人類社會中各種復雜系統[14]。其研究在許多領域都得到了應用，如金融網絡[15]、蛋白質網絡[16]、供需網絡[17]等。在進化計算領域，許多研究者也利用復雜網絡對GA 等進化算法進行了研究。文獻[18]將進化算法的動態可視化為復雜網絡，提出網絡進化算法框架，并應用于GA、粒子群算法和差分進化算法中。文獻[19]簡述了進化算法的動態性如何轉化為復雜網絡，并根據其網絡特征改進了自組織遷移算法、人工蜂群算法和GA 等算法。文獻[20]在蟻群算法的基礎上，在狀態轉移規則等中加入節點度系數，將改進算法用于移動Agent 問題中，顯著提高了移動Agent的遷移效率。文獻[21]利用復雜網絡分析了不同的隨機化對差分進化算法的影響。文獻[22]提出了一種基于復雜網絡的差分進化動力學建模方法，揭示了差分進化收斂速度與加權聚類系數之間的聯系。文獻[23]提出了一種動態小世界網絡來優化粒子群算法，提高了算法性能。文獻[24]將差分進化算法中個體看作節點，動力學傳播方向看作邊，提出利用個體的目標函數值及網絡參數信息依概率選取目標向量的機制，改變不同函數類型的收斂速度。文獻[25]將GA進化過程建模為復雜網絡，并設計一種自組織動態網絡結構，有效提高了GA的性能。文獻[26]利用不同網絡模型作為算法的底層結構，研究了不同網絡結構對進化算法動態性能的影響，發現網絡特性對算法的動態性和解的多樣性有顯著的影響。文獻[27]提出了一種基于復雜網絡的粒子群算法，并將該算法用于改進AdaBoost算法，縮短了樣本訓練時間，提高了人臉檢測率。

總的來說，現有研究利用復雜網絡來改進進化算法或者研究網絡結構對進化算法的影響時，它們大多是對算法個體間優勢基因的傳播構成的網絡進行研究，鮮有研究考慮子群間優勢基因的傳播構成的網絡結構對算法的影響，且較少考慮網絡結構參數的變化對算法的影響并從實際問題的角度進行分析。因此，不同網絡結構參數下網絡結構控制子群間優勢基因的傳播對MGA尋優性能的影響尚不清楚。現實生活中，許多網絡的節點度分布服從冪律分布，即無標度網絡[28]。現實復雜網絡的標度指數各不相同，有的網絡有核心節點存在但不具有無標度特性[29-30]。因此，本文利用不同標度指數的無標度網絡，或有核心節點但不具有無標度特性的網絡來設計MGA，得到一種含復雜網絡結構的多種群遺傳算法（Multi-population Genetic Algorithms with Complex Network Structures，MGA-CNS），然后以經典的柔性作業車間調度問題（Flexible Job shop Scheduling Problem，FJSP）[31]為例，利用MGA-CNS 來解決一個FJSP 基準測試問題，研究在解決實際問題時不同網絡結構參數對算法性能的影響。最后，將參數優化后的MGA-CNS來求解更多FJSP 實例并與多種其他算法進行比較，驗證其有效性。

綜上所述，為了了解在不同網絡結構參數下網絡結構控制子群間優勢基因的傳播對MGA 尋優性能的影響，本文進行了以下研究：（1）提出一種含復雜網絡結構的多種群遺傳算法；（2）通過仿真控制網絡結構參數的變化，研究網絡結構參數對算法尋優性能的影響。

1 模型與算法

1.1 柔性作業車間調度問題

FJSP由Brucker等[31]提出，可以簡單地描述為：在一個車間有m 臺機器(M1,M2,…,Mm) 對n 個工件(J1,J2,…,Jn) 進行加工。其中，每個工件Ji有若干個工序，分別記為：Oi1,Oi2,…,Oini。每個工序可以在一個候選機器集上進行加工，第i 個工件第j 個工序的候選機器集記為Sij，其在第k 臺機器(Mk)上進行加工的時間表示為Pijk。每臺機器一次只能加工一個工序，同一工序可在多臺機器上進行加工，但每個工序每次只能在一臺機器上加工。FJSP 可以分為兩個子問題：一是為每個工件的每個工序選擇合適的機器，另一個是為分配給同一機器的所有工序安排合適的加工順序。FJSP通常有最小化最大完工時間和最小化最大機器工作載荷等優化目標。本文以研究算法性能為目的，因此選擇最常用的最小化最大完工時間為優化目標，FJSP 的數學模型如下所示[7]：

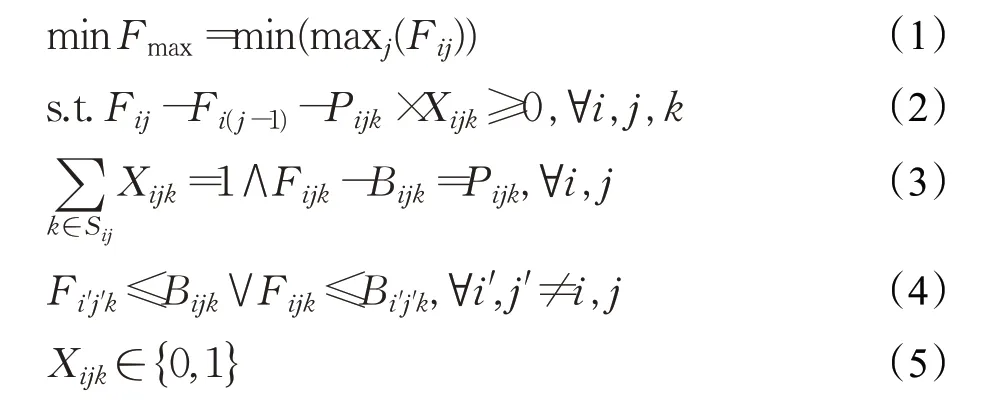
公式（1）表示目標函數，即最小化最大完工時間。Fij和Fmax分別表示工序Oij的完工時間和所有作業的最大完工時間。公式（2）表示工藝約束，確保了同一工件的所有工序的正確加工順序，當工序Oij在第k 臺機器上進行加工時，Xijk等于1，否則為0。公式（3）表示每個工序每次只能在一臺機器上加工，Bijk和Fijk分別表示工序Oij在第k 臺機器上的加工開始時間和加工完成時間。公式（4）表示每臺機器一次只能加工一個工序。其中，符號“∧”和“∨”分別表示邏輯與和邏輯或。表1給出了一個FJSP例子。

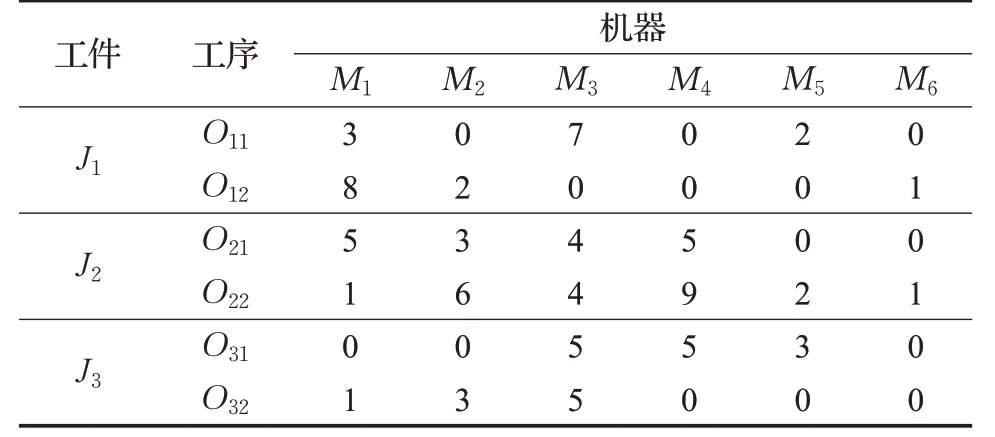
表1 一個FJSP例子

在表1的例子中，給出了三個工件，六臺機器，每個工件都有兩個工序。其中，數字0表示該工序不能在對應的機器上進行加工，其余數字表示工序Oij在機器Mk上的加工時間。比如，第五行第一列的0 表示第三個工件的第一個工序O31不能在機器M1上進行加工，第二行第一列的8表示第一個工件的第二個工序O12在機器M1上的加工時間為8。

1.2 含復雜網絡結構的多種群遺傳算法

生成無標度網絡的模型中，最經典的當屬BA 模型[28]。BA 模型的主要特點是增長和優先連接，其節點度(K)服從冪律分布：K-γ（γ 為標度指數）。然而，由BA模型所生成的無標度網絡的標度指數接近一個常數(γ=3)，但實際復雜網絡的標度指數各不相同，也有的網絡不具有無標度特性，但總有核心節點的存在[29-30]。因此，本文利用文獻[29]和[32]提到的參數可控的復雜網絡模型，生成不同標度指數的無標度網絡，或生成含有核心節點但不具有無標度特性的網絡，以研究不同網絡結構參數對MGA的影響規律。該模型可描述如下：

從一個初始規模為m0（初始節點數為m0）的全連接網絡開始，每一時間步t 引入一個新節點j，每個新節點j 與m(≤m0)個老節點相連接，不允許重邊與自環。老節點i 被選擇的概率與其產生核(Ai)有關，表示為：

式（6）中，?k 表示求和號涵蓋所有老節點，Ai表示為：

其中，α 和β 是兩個可控參數，Ki為節點度（節點i 的鄰居節點數量）。當β 不變時，不同的α 值可生成不同標度指數的無標度網絡。當α 不變時，不同的β 值可生成含有核心節點但不具有無標度特性的網絡。圖1 繪出了具有12個節點的無標度網絡示意圖。

圖1（a）繪出了其網絡結構，圖1（b）中，橫軸按節點度對12個節點進行排序，縱軸表示相應的節點度。

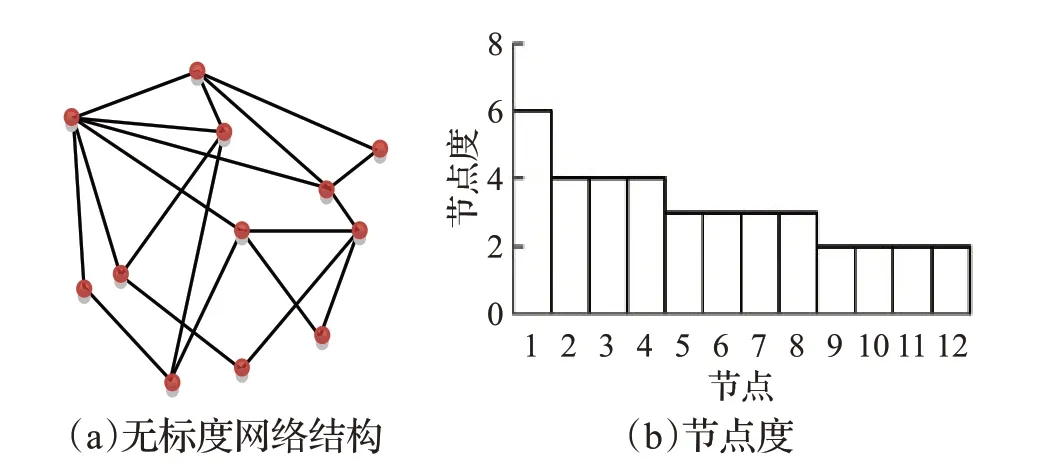
圖1 一個含有12個節點的無標度網絡

如前所述，MGA將標準GA的單種群劃分為多個子群，這些子群構成節點，子群之間優勢基因的傳播構成邊，不同的連接構成了不同的網絡結構。MGA 中所有子群的數量稱為子群數，每個子群的個體數量稱為子群大小[7]。MGA 在執行過程中，首先進行種群初始化，生成N 個子群，每個子群的大小為S。然后，所有子群中的個體都同時進化，都會根據適應度函數來評價個體，根據精英制選擇精英個體，精英個體在子群間遷徙，從而優勢基因在不同子群之間進行傳播，產生新一代子群，實現優勝劣汰的進化過程，直到得到最優解。

本文利用上述網絡模型生成的網絡來設計MGA，控制子群間優勢基因的傳播，得到MGA-CNS。節點就是MGA-CNS 的子群，用V 表示節點集合；邊就是子種群間優勢基因的傳播，用E 表示邊集合；若節點Vi與Vj連接構成邊eij，則eij∈E 。MGA-CNS 的流程圖如圖2所示，具體步驟如下：

步驟1 初始化，根據編碼規則隨機初始化N 個子群，每個子群中的個體數量為S。

步驟2 判斷是否達到最大迭代次數，如果當前迭代次數(Inow)等于最大迭代次數(Imax)，則輸出最優解，并結束計算，否則，轉向步驟3。

圖2 MGA-CNS的流程圖

步驟3 用解碼算法計算每個子群中個體的適應度，將精英個體保存到精英集合中。

步驟4 根據適應度，采用標準的競標賽方法選擇每個子群的下一代個體。

步驟5 將得到的個體隨機進行交叉，產生新的個體。

步驟6 將得到的個體根據變異概率(Pr)進行變異產生新的個體。

步驟7 隨機選擇一個子群（節點Vi），根據設計的網絡，找到節點Vi的所有鄰居節點，找到這些節點（包含節點Vi）中最好的精英個體，將它放入這些節點中，并保持它們的子群規模不變。返回步驟2。

圖3 給出了一個含四個子群的MGA-CNS，每個子群含有四個個體，個體間通過遺傳算子進化，子群間通過精英個體的遷徙傳播優勢基因。

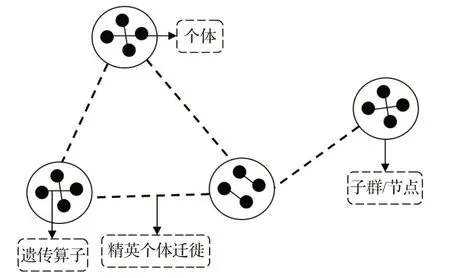
圖3 MGA-CNS的示意圖

1.3 MGA-CNS解決FJSP

MGA-CNS 在求解FJSP 時，包含四個主要的操作，分別是編碼、解碼、交叉和變異。

1.3.1 編碼

使用MGA-CNS 解決FJSP 時，第一步是知道如何得到一個暫定的編碼解。文獻[5]中描述了使用整數編碼方法來獲得編碼解。整數編碼分為兩個階段：第一個階段為機器編碼，第二個階段為工序編碼。

在機器編碼階段，用一個整數串表示編碼解；整數串的數量表示所有工件的工序總數量，整數的位置表示工序，整數的數值代表候選機器中加工該項工序的機器序號。例如表1 中的FJSP 例子，一共有六個工序，一個編碼解為（3 3 2 1 3 1）。這個整數串里一共有六個整數，代表一共有六個工序。第一個整數3 代表了工序O11在候選機器中的第三臺機器中進行加工，即機器M5而不是M3。第二個整數3 代表了工序O12在機器M6上進行加工，以此類推。

在工序編碼階段，用一個整數串表示編碼解，整數串的數量表示所有工件的工序總數量，整數的位置表示加工順序，整數的值表示工序號。如果一個工件有n 個工序，那么這個工件號就會出現n 次。例如表1中的例子，工序編碼解為（2 1 2 3 1 3）。這個整數串里一共有六個整數，代表一共有六個工序。1、2、3分別出現了兩次，這代表工件1、2、3分別有兩項工序。第一個整數2 代表這次加工工序O21，第二個整數1 代表這次加工工序O11，第三個整數2代表這次加工工序O22，以此類推。

將兩個階段得到的機器編碼解和工序編碼解結合起來考慮會得到，先是在機器M2上加工工序O21，然后，在機器M5上加工工序O11，接著在機器M1上加工工序O22，以此類推。從而，整數串（3 3 2 1 3 1 2 1 2 3 1 3）代表了一個個體。

1.3.2 解碼

為了獲得最終可行的解決方案，需要對編碼的個體進行解碼。文獻[5]提出的解碼算法被用于從個體中獲得解決方案。還以表1 的FJSP 為例，考慮個體（3 3 2 1 3 1 2 1 2 3 1 3），可以得到的解為一個矩陣M′=[2 1 2 3 0 0；1 1 5 2 0 0；2 2 1 1 0 0；3 1 5 3 0 0；1 2 6 1 0 0；3 2 1 1 0 0]。第一個整數表示工件號，第二個整數表示該工件的工序號，第三個整數表示加工該工序的機器號，第四個整數表示在該機器上的加工開始時間，第五個整數表示在該機器上的加工結束時間。例如（2 1 2 3 0 0）就表示的是第二個工件的第一個工序由第二臺機器M2加工，加工時間為P212=3。但開始和結束時間未知（用0表示），以此類推。

開始和結束時間初始化都為0。用Bijk表示工序Oij的加工開始時間，Fijk表示工序Oij的加工結束時間，加工結束時間等于加工開始時間加上加工時間。分為四種情況討論，如表2所示。所有情況要保證考慮到了所有M′行。

表2 一個FJSP例子

1.3.3 交叉

交叉和編碼一樣分為兩個階段，第一個階段為機器交叉，第二個階段為工序交叉。在機器交叉階段，隨機生成兩個小于工序總數的整數，以這兩個隨機整數為節點實現兩點交叉，如圖4（a）。在工序交叉階段，如文獻[5]所描述，隨機選擇兩個個體（父代1和父代2），所有工序被隨機分成兩組（第一組和第二組），那么子代1和子代2分別繼承父代1和父代2的屬于組1和組2的整數，同時保留這些整數的位置，子代1 和子代2 分別繼承父代2和父代1 的不屬于組1 和組2 的整數，并保留這些整數的序列，如圖4（b）。

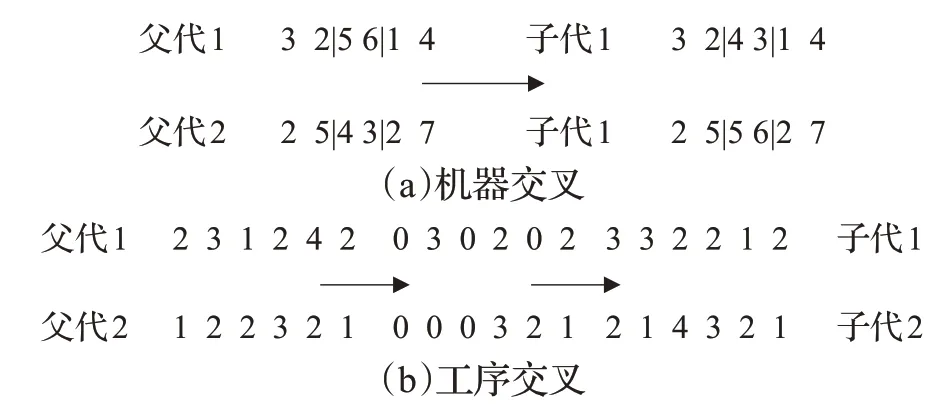
圖4 交叉運算

1.3.4 變異

變異保持了個體的多樣性，是MGA-CNS的主要算子之一。變異也分為兩個階段。第一個階段是機器變異階段，第二個階段是工序變異階段。在機器變異階段，根據變異概率隨機選擇幾個個體，然后在選中的每個個體中再隨機選擇幾個位置，用幾個小于機器總數的整數來替換這幾個位置上的整數。在工序變異階段，也是根據變異概率隨機選擇幾個個體，隨機產生兩個小于工序總數的整數，這兩個整數代表了被選中個體上的兩個位置數，同時代替被選中個體這兩個位置上的整數。

1.4 評價指標

標準GA 按與個體適應度成正比的概率來決定當前種群中每個個體能遺傳到下一代種群中的機會多少。在MGA-CNS 中，除了考慮個體適應度以外，還要考慮子群的適應度。正如文獻[7]所描述的，MGA 的本質是一種隨機搜索算法，具有一些控制條件，算法的個體總數(TIN) 越大，算法的性能應該越好。因為，當TIN 越大時，算法搜索的次數就越多，就應該能找到更優的解。MGA-CNS的TIN 計算公式如下：

S 代表子群大小，N 代表子群數，TG 代表相應MGACNS 的總代數。當某一變量改變時，TIN 會有很大的不同。例如，有A和B兩個MGA-CNS，A和B的TG 都為100，但是它們的S 和N 不同，A的S 和N 為40，40，B的S 和N 為400，400，那么A和B的TIN 分別為160 000和16 000 000。理論上說，B能找到更優的解，但如果它們找到相同的解，則A 要好得多，因為它找到同樣優的解所用的搜索次數更少。

如文獻[5]中所述，他們在解決FJSP時，采用的最大的TIN 是100萬。為了使子群擁有更多交流機會，本文采用的最大的TIN 為200 萬。如前所述，FJSP 的目標是盡量縮短最大完工時間。因此，使用基于TIN 的最大完工時間來評估MGA-CNS的性能，其中較小的最大完工時間表示較好的MGA-CNS。每個算法獨立運行Nt次，得到的最大完工時間的平均值稱為平均最優值，用于評估MGA-CNS的性能。并且，還通過計算成功率(SR)來評價MGA-CNS 的優劣，成功率越高，則表示算法越好。成功率的計算公式如下：

這里的Ns表示式中所用算法在Nt次運行中能夠找到所解決的FJSP的最優解的次數。

2 仿真研究

2.1 實驗設置

使用一個10×10FJSP 實例[7]來測試MGA-CNS，研究所使用網絡的結構參數是怎樣影響MGA-CNS 的性能。分別進行以下幾個實驗：

實驗1 子群大小S 對MGA-CNS性能的影響；

實驗2 子群數N 對MGA-CNS性能的影響；

實驗3 可控參數α 對MGA-CNS性能的影響；

實驗4 可控參數β 對MGA-CNS性能的影響；

實驗5 初始網絡規模m0對MGA-CNS性能的影響。

為了保證實驗的準確性，在分別測試網絡結構參數S、N、α、β 和m0對MGA-CNS的影響時，除了被測參數按規則變化外，其余參數均保持不變。

2.2 子群大小S 對MGA-CNS性能的影響

研究子群大小S 對MGA-CNS 性能的影響。相關參數的設置如下：Pr=0.08,N=100,TIN=2 000 000，α=1,β=1,m0=2,S 以20 為步長從10 變化到200，Nt=20。圖5 給出了平均最優值和成功率隨S 的變化情況。

如圖5 所示，當S=20 時，MGA-CNS 的性能較差，平均最優值為8.9，成功率為40%。隨著子群大小的擴大，MGA-CNS 的性能變好。當S=60 時，平均最優值為7.5，成功率為50%。當子群大小在60 到100 之間擴大時，MGA-CNS 性能逐漸變差。當S=100 時，平均最優值為7.7，成功率為30%。當子群大小大于100 時，隨著子群大小的擴大，平均最優值減小，成功率增加。因此，子群大小最好大于100，并且子群越大，MGA-CNS性能越好。

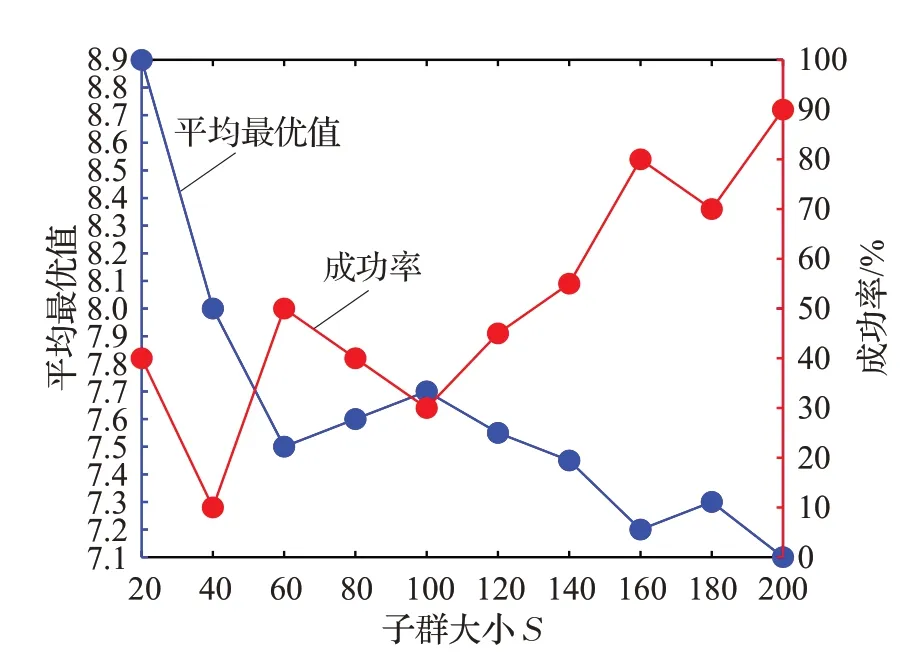
圖5 平均最優值和成功率隨子群大小的變化情況

2.3 子群數N 對MGA-CNS性能的影響

研究子群數N 對MGA-CNS 性能的影響。相關參數的設置如下：Pr=0.08,S=40,TIN=2 000 000,α=1,β=1,m0=2,N 以10 為步長從10 變化到200，Nt=20。圖6給出了平均最優值和成功率隨N 的變化情況。

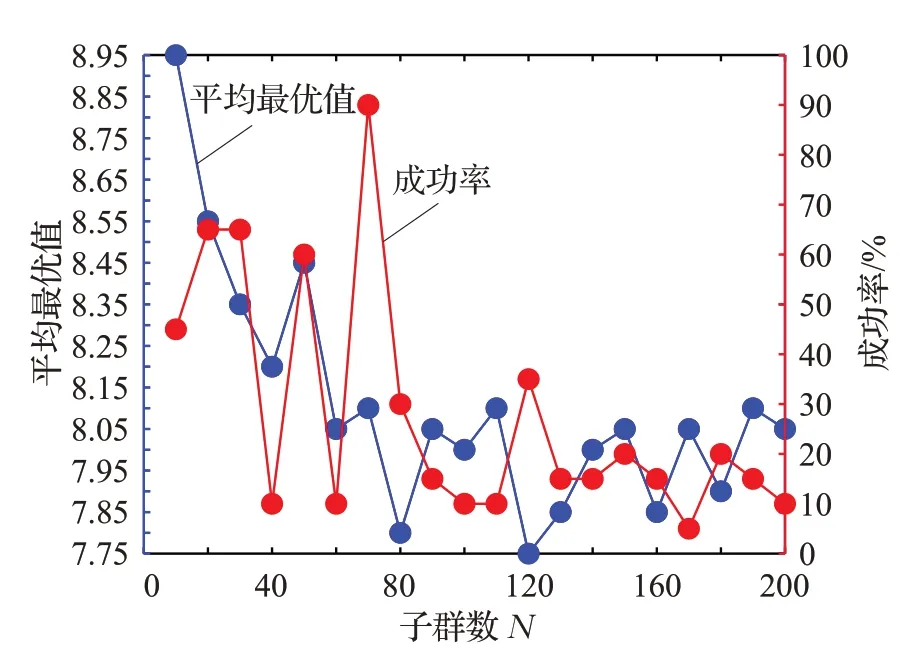
圖6 平均最優值和成功率隨子群數的變化情況

如圖6所示，當N=10 時，平均最優值為8.95，成功率為45%，MGA-CNS 的性能較差。隨著N 的增加，MGA-CNS的性能變好。當N=70 時，平均最優值為8.1，成功率為90%。隨著N 的進一步增大，平均最優值逐漸減小，但是成功率也逐漸降低。因此，為了使MGA-CNS的性能較好，N 不能取值過小，更不能取值過大。

2.4 參數α 對MGA-CNS性能的影響

研究可控參數α 對MGA-CNS 性能的影響。相關參數的設置如下所示：Pr=0.08,S=40,N=100,TIN=2 000 000,β=1,m0=2,α 從0.1變化到20，當從0.1變化到1時，步長為0.1，當從1變化到20時，步長為2，Nt=20。如文獻[29]所述，通過調整α 的值可以生成不同標度指數的網絡。當α 從0 變化到1 時，標度指數從無窮大趨近于3，由于0 到1 的區間較小，因此以0.1 為步長；當α大于1 時，標度指數小于3，此時α 可調區間較大，因此以2為步長。圖7給出了平均最優值和成功率隨α 的變化情況。

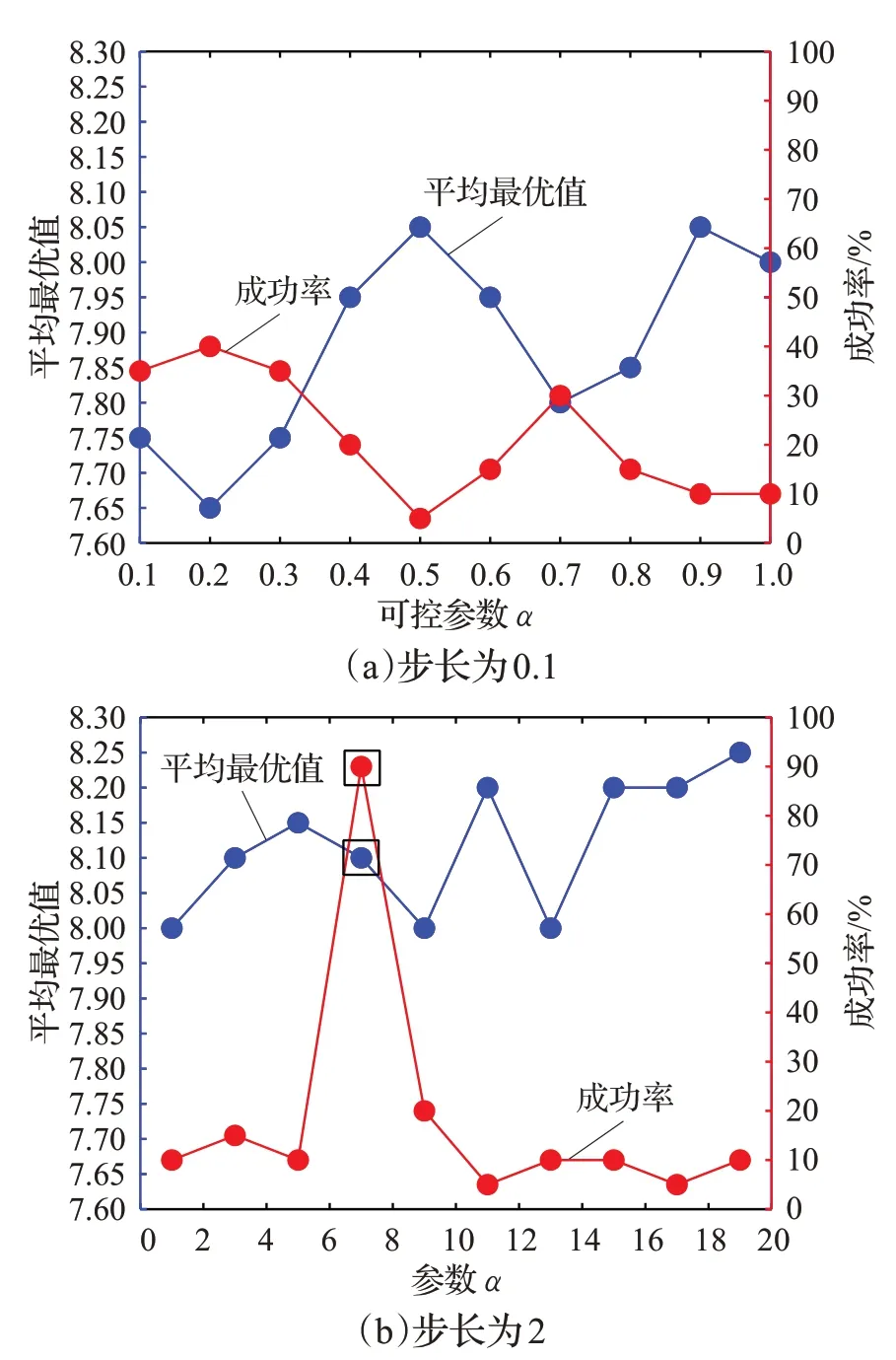
圖7 平均最優值和成功率隨α 的變化情況

在圖7 中，當α=0.1 時，平均最優值為7.75，成功率為35%，MGA-CNS 的性能較好。當α 大于0.3 時，平均最優值顯著上升，而成功率顯著下降，這說明MGA-CNS的性能也顯著下降。隨著α 的增加，平均最優值總體呈上升趨勢，而成功率總體呈下降趨勢（不考慮α=7 時的異常，見圖7（b）中標注點）。這意味著，當α 較大時，MGA-CNS的性能反而會降低。當α=0.2 時，MGA-CNS的性能達到最優，平均最優值為7.65，成功率為40%，但α 在區間[0.1，0.3]變化時，算法性能波動不大，α=0.2 的左右兩個區間表現相同的趨勢，都具有較好的性能。因此，為了獲得更好的MGA-CNS，α 不能太大，更具體地說，當α 的值不大于0.3時，MGA-CNS的性能更好。

2.5 參數β 對MGA-CNS性能的影響

研究可控參數β 對MGA-CNS 性能的影響。相關參數如下：Pr=0.08,S=40,N=100,TIN=2 000 000,α=1,m0=2,β 從0.2變化到3，步長為0.2，Nt=20。圖8給出了平均最優值和成功率隨β 的變化情況。

在圖8 中，當β=0.2 時，平均最優值為7.7，成功率為35%，此時，MGA-CNS的性能最優。隨著β 的增加，平均最優值總體呈上升趨勢，它先隨著β 的增加而增加，當β 在2.2和2.8之間擴大時，平均最優值隨之減小，之后，平均最優值又隨著β 的增加而增加。與平均最優值相反，成功率呈下降趨勢，特別是，當β 大于0.8 時（圖8中圓圈標注點），成功率顯著下降，當β 大于1時，成功率的波動較小，基本趨于穩定（不考慮β=3 和3.2時的異常，見圖8 中矩形標注點）。這意味著，MGACNS 的性能先隨著β 的增加而下降，然后隨著β 的增加而增加，再隨之下降，總體呈下降趨勢。根據平均最優值和成功率的變化可看出，β 在區間[0.2，0.8]變化時，MGA-CNS 可獲得較好的性能，且越往后，MGACNS的性能越差。因此，為了獲得更好的MGA-CNS，β的取值不能太大，更具體地說，當β 的值不大于0.8時可以得到較好的MGA-CNS。

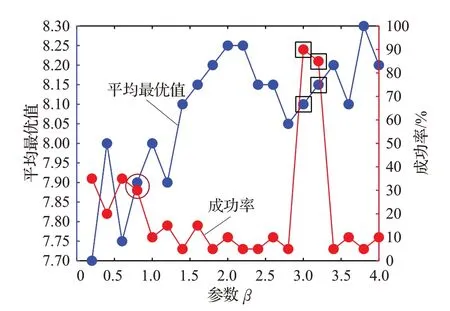
圖8 平均最優值和成功率隨β 的變化情況

2.6 初始網絡規模m0 對MGA-CNS性能的影響

研究初始網絡規模m0對MGA-CNS 性能的影響。相關參數的設置如下：Pr=0.08,S=40,N=100,TIN=2 000 000,α=1,β=1,m0從2變化到10，步長為1，Nt=20。圖9給出了平均最優值和成功率隨m0的變化情況。

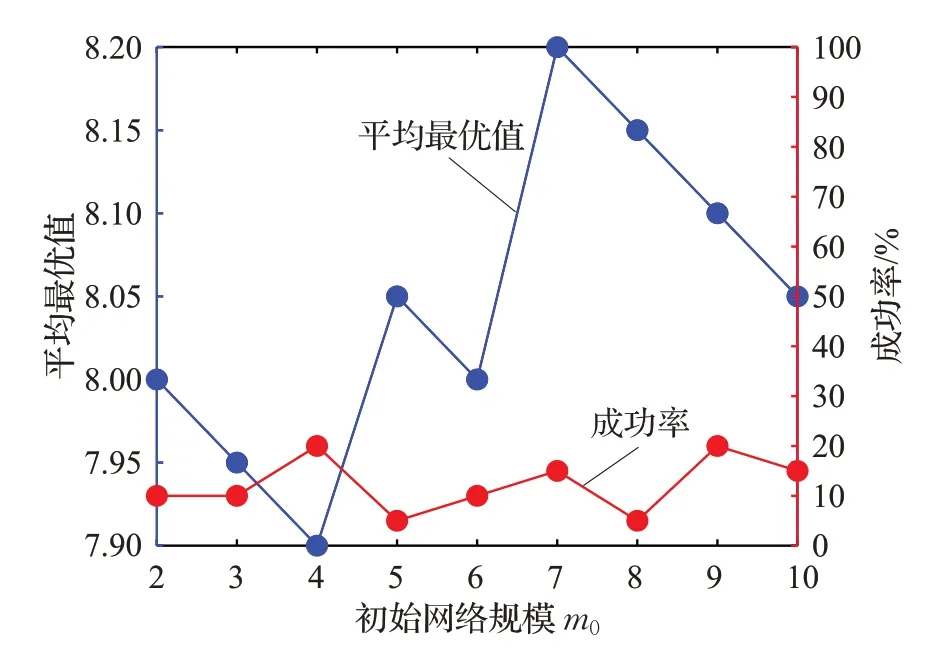
圖9 平均最優值和成功率隨初始網絡規模的變化情況

如圖9 所示，隨著m0的增加，平均最優值在7.9 和8.2 之間波動，成功率在5%和20%之間波動。當m0=4時，平均最優值取得最小值為7.9，成功率取得最大值為20%，此時，MGA-CNS 的性能較好。仔細觀察可以發現，雖然平均最優值一直在上下波動，但總體呈上升趨勢，而成功率波動較小，基本趨于穩定。這意味著，MGA-CNS 的性能隨著m0的增加而下降。因此，為了獲得更好的MGA-CNS，m0的取值不能太大，當m0不大于4時可以得到較好的MGA-CNS。

2.7 MGA-CNS求解FJSP的有效性

以文獻[33]提到的18個FJSP實例為例，驗證MGACNS 的有效性。通過前文的研究，確定相關參數：Pr=0.08,S=200,N=70,TIN=2 000 000,α=0.2,β=0.2,m0=4,Nt=20。表3給出了用MGA-CNS求解文獻[33]提到的18個FJSP實例與文獻[34-37]所提算法求解的比較結果。圖10給出了求解MFJS08得到的甘特圖。

圖10 MFJS08實例的甘特圖

表3中，文獻[34]有AIS和HHS兩種算法，符號“—”表示原文沒有給出相應數據。用MGA-CNS 求解MFJS02 時最優值為446，比文獻[34]的448 更優；求解MFJS05 時最優值為514，比文獻[34]的527 更優；求解MFJS06 時最優值為634，比文獻[34]的635 更優；求解MFJS04 時最優值為554，比文獻[35]的564 更優；求解MFJS07時最優值為881，比文獻[35]的928更優；說明了MGA-CNS的有效性。

2.8 結果分析

標準GA 有一個非常明顯的缺點，就是過早收斂。GA 靠交叉算子把父代的優勢基因遺傳給子代，使優勢基因很快就積累起來，而很少破壞它們，這導致GA 可以非常快速地獲得局部最優值。在之前的很多文獻中都提出了很多解決這個問題的辦法，而本文提到的MGA-CNS也同樣是為了解決GA過早收斂的問題。當MGA-CNS的不同子群彼此交流時，優勢基因不僅能夠在子群內進行傳播，而且還能在子群之間進行傳播。子群之間優勢基因的傳播主要受其網絡結構控制，已有研究表明，網絡平均路徑長度越小，優勢基因傳播速率越高[29]。本文研究了五個網絡結構參數（S、N、α、β 和m0）分別在其余參數都不改變的情況下對MGA-CNS的影響。

如2.2 節所述，在一定的TIN 下，隨著S 的增大，MGA-CNS 的性能先逐漸提高，然后逐漸降低，當S 大于100后，MGA-CNS的性能又逐漸提高。S 越大，平均最優值越小，成功率越高，此時更容易得到最優解，MGA-CNS 的性能就越好。因為，當S 很小時，子群中個體的數量較少，此時基因池較單一，存在多樣性不足的問題，容易早熟收斂，所以此時的算法性能較差；而隨著S 的增加，子群中的個體數量增加，子群中的多樣性得到了保持，所以算法性能越來越好。

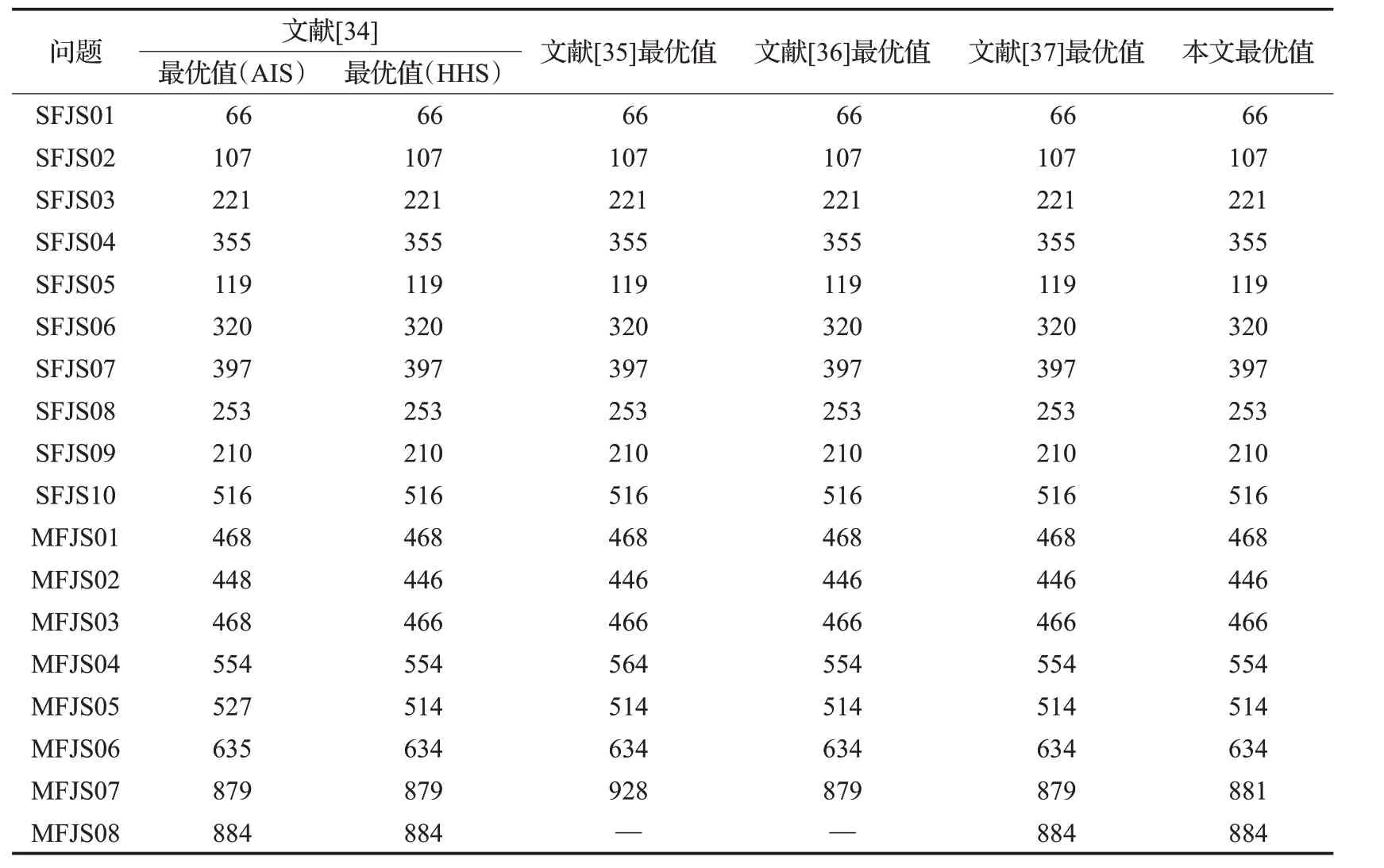
表3 比較結果

如2.3 節所述，在一定的TIN 下，隨著N 的增大，MGA-CNS 的性能先逐漸提高，隨后又逐漸降低，為了使MGA-CNS的性能較好，N 不能取值過小，更不能取值過大。這是因為，當N 值很小時，子群個數過少，不利于子群之間的交流，但是又因為每個子群的規模適當，所以MGA-CNS的性能不會太差。隨著N 的增大，子群個數變多，更有利于保持種群多樣性，所以MGACNS的性能逐漸變好，但是當N 進一步增大時，一次迭代所用的個體數很多，又因N 是一個定值，所以總的迭代次數很少，個體來不及積累優勢基因，MGA-CNS 的性能也就變差。因此，可以得出如文獻[38]所述的結論：在一定的總個體數下，多代尋優是合理的策略。

如2.4 節所述，在一定的TIN 下，隨著α 的增大，MGA-CNS 的性能逐漸降低。因此，為了獲得更好的MGA-CNS，α 的取值不能太大，更具體地說，當α 的值不大于0.3時，MGA-CNS的性能更好。因為，當α 較小時，網絡中具有更多的高節點度的節點，網絡的連接性更好，網絡的平均路徑長度較小，從而子群間優勢基因的傳播速率較高，更有利于保持種群多樣性且較快地獲得最優解，所以α 的取值不能太大。

如2.5 節所述，在一定的TIN 下，隨著β 的增大，MGA-CNS 的性能先逐漸降低，再逐漸提高，然后又逐漸降低，總體呈下降趨勢。為了獲得更好的MGA-CNS，β 的取值不能太大，當β 不大于0.8 時，MGA-CNS 的性能較好。因為，當β 較大時，網絡中會出現一個凝聚點，這個節點幾乎與其他所有節點連接[32]。此時，網絡的平均路徑長度非常小，子群間優勢基因傳播速率非常高，MGA-CNS將非常快速地獲得局部最優值，從而導致早熟收斂。所以，當β 大于0.8時算法性能會變差。

如2.6 節所述，在一定的TIN 下，隨著m0的增大，MGA-CNS 的性能逐漸降低。因此，為了獲得更好的MGA-CNS，m0取值不能太大，當m0不大于4時可以得到較好的MGA-CNS。這是因為，當m0越大時，新引入的節點與網絡中具有高節點度的節點連接的概率越大，這意味著優勢基因將很少傳播到其他的子群，便無法從其他精英個體中獲益，所以，m0取值不能太大。

3 總結

GA 在處理組合優化等問題上具有獨特的優勢，但是卻容易出現早熟收斂的問題。為了克服這一缺點，多種群是一種有效的方法。但以往研究中，往往忽略了子群間優勢基因的傳播構成的網絡結構對算法的影響，沒有考慮到某些網絡結構參數（S、N、α、β 和m0）對MGA 的影響。因此，本文設計了一種含復雜網絡結構的多種群遺傳算法（MGA-CNS）來對這五個參數對算法性能的影響規律進行研究。

仿真結果表明，子群大小S 的取值最好大于100，并且S 越大，MGA-CNS的性能越好；為了使MGA-CNS的性能較好，子群數N 不能取值過小，更不能取值過大；可控參數α 的值不能太大，更具體地說，當α 不大于0.3時，MGA-CNS的性能更好；可控參數β 的取值不能太大，當β 不大于0.8 時，可以得到較好的MGA-CNS；為了獲得更好的MGA-CNS，初始網絡規模m0的取值也不能太大，當m0不大于4時，MGA-CNS的性能更好。

本文研究了用MGA-CNS 解決組合優化問題時不同網絡結構參數對算法的影響，但是在優化問題中還有連續優化問題。另外，多種群能夠改善GA 的性能，而入侵雜草優化算法（Invasive Weed Optimization，IWO）[39]的改善不能僅靠多種群[5]，所以在今后的研究中會對連續優化問題和IWO的性能改善進行進一步的研究。