經驗小波神經網絡在電離層TEC短期預測中的應用

黃佳偉，魯鐵定，魯春陽，劉 盈

(1.東華理工大學測繪工程學院，330013，南昌；2.河南城建學院測繪與城市空間信息學院，467036，河南，平頂山；3.井岡山大學電子與信息工程學院，343009，江西，吉安)

0 引言

作為近地空間環境的重要組成部分，電離層對無線電通信、導航，衛星定位和遙感、遙測等有著重要的影響[1]。建立電離層總電子含量(Total Electric Contents，TEC)預測模型不僅為研究電離層的時空變化規律提供模型基礎，也對研究地震異常探測等具有重要意義[2-3]。目前，國內外對電離層TEC值的預測根據時間長短可分為長期預測和短期預測。長期預測主要有利用TEC觀測數據構建經驗模型和參考電離層模型，如本特(Bent)模型、國際參考電離層模型IRI、克羅布歇(Klobuchar)模型等，其中以Klobuchar模型應用最廣[1,4]。短期預測主要分為經典數學統計法和人工智能法，具體包括時間序列分析法、灰色預測模型和神經網絡模型等[5-8]。如陳鵬等利用時間序列分析的方法對TEC數據進行預報，預測效果較好[5]。胡勇等提出將灰色理論運用于電離層預測當中，結果表明預測效果可行[6]。李淑慧等利用神經網絡中的BP神經網絡構建提前一天的TEC預報模型，結果表明預報模型可以反映不同季節的TEC變化特征[7]。然而電離層時空變化的復雜性給預報帶來一定的影響，直接使用模型預測TEC數據無法達到滿意的預報精度[8]。本文引入經驗小波變換(Empirical Wavelet Transform，EWT)對電離層TEC數據進行分解，結合BP神經網絡(Back Propagation Network)建立EWT-BP組合預測模型，以提高預報精度。

1 算法原理

1.1 BP神經網絡模型

人工神經網絡(Artificial Neural Network，ANN)是在現代神經科學研究成果的基礎上提出的技術。它的基本處理單位為神經元，將大量的神經元以各種方式連接來建立非線性神經系統，處理各種復雜的數據。其中，在處理多維函數逼近、復雜模式識別和非線性時間序列預測等問題時，BP神經網絡得到最廣泛的應用。

BP神經網絡(Back Propagation Network)又稱反向傳播神經網絡，最早由Rumelhart和McClelland等科學家于1986年提出，因其具有較強的非線性映射能力和柔性的網絡結構，在非線性時間序列預測方面的應用較為廣泛[9]。圖1為3層BP神經網絡結構示意圖，從圖1中可以看出BP網絡是由輸入層、隱含層和輸出層3部分組成的，其中隱含層可以有一層或多層。相鄰層次的神經元之間實現全連接，而獨立層次的神經元之間無任何連接。

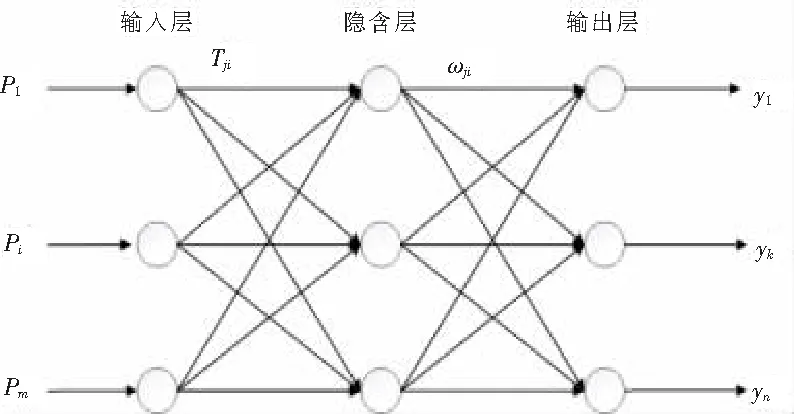
圖1 3層BP網絡結構圖

BP神經網絡的構建可分兩步過程進行，即信號的前向傳播和誤差的反向傳播，通過不斷調整神經元之間的網絡參數(權值和閾值)，使實際輸出逼近期望輸出，達到最小誤差均方差，其具體步驟如下[9]。

1.1.1 信號的前向傳播 選擇一組數據訓練樣本，將其分為輸入數據和期望的輸出數據；輸入數據從輸入層進入到神經網絡，經過隱含層逐層處理后作用于輸出層，經過非線性變換產生輸出信號；計算網絡輸出和期望輸出的誤差函數，若誤差滿足目標要求，則網絡建立成功，否則進入反向傳播過程。

1.1.2 誤差的反向傳播 反向傳播時，將輸出誤差通過隱含層向輸入層逐層反轉，將誤差分攤給各層的所有神經元，已從各層收集的誤差信號作為調整權值和閾值的依據。通過不斷修正輸入層與隱含層的權值和閾值以及隱含層和輸出層的權值和閾值，使誤差函數沿梯度方向下降，直到整個訓練樣本的誤差達到要求為止。

誤差函數[10]可表達為：

(1)

(2)

式中：p為數據個數，k為迭代次數，tl為期望輸出，Ol為神經網絡現行輸出，ek為單個數據誤差函數，E為總體誤差函數。

1.2 經驗小波變換

經驗小波變換(Empirical Wavelet Transform，EWT)是Gilles[11]及其團隊于2013年提出的一種基于信號頻譜劃分的信號處理新方法。與EMD缺乏嚴格的理論支撐不同，EWT依靠小波分析理論框架，根據信號自身性質產生基函數。其核心思想是根據信號頻譜劃分結果建立小波濾波器組，來提取信號的不同模態[12]。

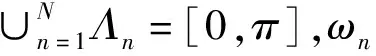
圖2 傅里葉頻譜劃分

經驗尺度函數可表達為：

(3)

經驗小波函數可表達為：

(4)

其中τn和β(x)可表達為：

(5)

重構的原始信號可表達為：

(6)

經驗小波分解的模態可定義為：

(7)

(8)

1.3 EWT-BP組合模型的建立

圖3為EWT-BP模型算法流程圖。

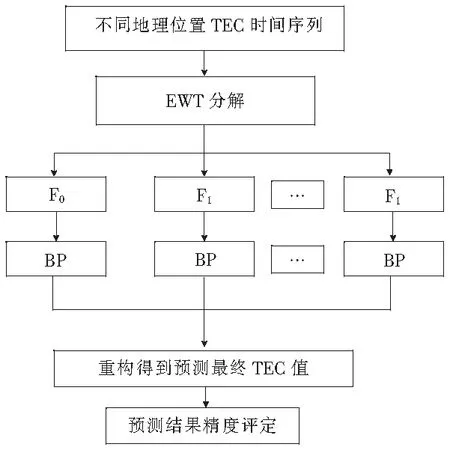
圖3 EWT-BP算法流程圖

將EWT算法應用到電離層TEC數據處理當中，首先利用EWT將不同位置處的TEC時間序列進行分解，得到不同模態分量的子時間序列，再利用BP神經網絡對不同分量進行預測，預測結果疊加得到最終預測值。具體步驟如下。

1)利用EWT將TEC時間序列x(t)分解為一個經驗尺度分量f0，代表信號整體變化趨勢，k個經驗小波分量fi，代表信號不同頻域特征，即：

(9)

2)對分解后的經驗尺度分量和經驗小波分量分別建立BP網絡模型進行預測，疊加分量預測結果得到最終TEC預測值。為減小疊加誤差對最終TEC值的影響，因其信號能量主要集中在經驗尺度分量和前2個經驗小波分量，只取EWT分解的經驗尺度分量f0和經驗小波分量f1和f2，其結果不會對預測效果產生太大影響[13]。以IGS中心發布的TEC值作對比數據，采用日平均相對精度P和均方根誤差RMSE作為評定預測效果的指標，可表達為：

P=1-|It-I|/I

(10)

(11)

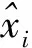
2 實驗結果與分析

提取IGS中心提供的2010年電離層格網數據進行實驗，參照文獻[8]，分別選取年積日為1～30、101～130、201～230和301～330 的4個不同時間段低緯(a.15°N，125°E)、中緯(b.45°N，60°W；c.45°N，125°E)、高緯(d.75°N，125°E)的TEC時間序列進行實驗，每個時間段的年積日個數為30。將前24 d的數據作為輸入，第25天的數據作為輸出，組成訓練樣本，第2天到第25天的數據作為輸入，來預測第26天的數據，以此類推，預測后5 d的數據，后5 d的數據作為真實值來檢測模型預測效果。

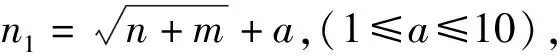
以年積日201～230時間段為例進行具體分析，對比分析EWT-BP組合模型和單一BP模型的預測效果。圖4為年積日226～230的4個不同地理位置2種模型的TEC預測結果與TEC真實值對比圖。其中橫坐標為5 d內預測歷元的個數，時間間隔為2 h；縱坐標為TEC值，單位為TECU的個數，1 TECU=1016e/m2。圖4結果顯示，相對于單一BP模型的預測結果，EWT-BP模型預測結果與真實值更加吻合，預測誤差更小，表明EWT-BP模型能夠更好地反映電離層TEC的變化特征，預測效果更優。

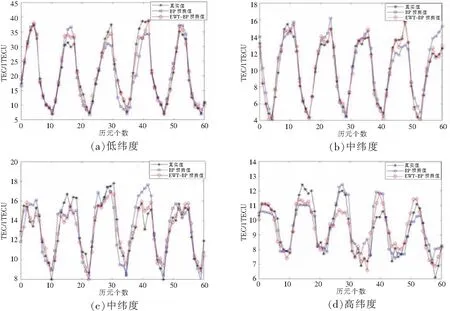
圖4 不同地理位置2種模型的預報TEC值對比圖

表1從整體上反映了2種模型的殘差誤差分布情況。從表1可以看出，BP神經網絡模型預報的5 d內平均殘差絕對值小于1個TECU占比為66.8%，平均殘差絕對值大于3個TECU占比為6.4%；而EWT-BP模型預報的5 d內平均殘差絕對值小于1個TECU占比為79.7%，平均殘差絕對值大于3個TECU占比為2%。結果表明，組合模型的預測效果整體上要優于單一模型的預測效果，與圖4結果相符。

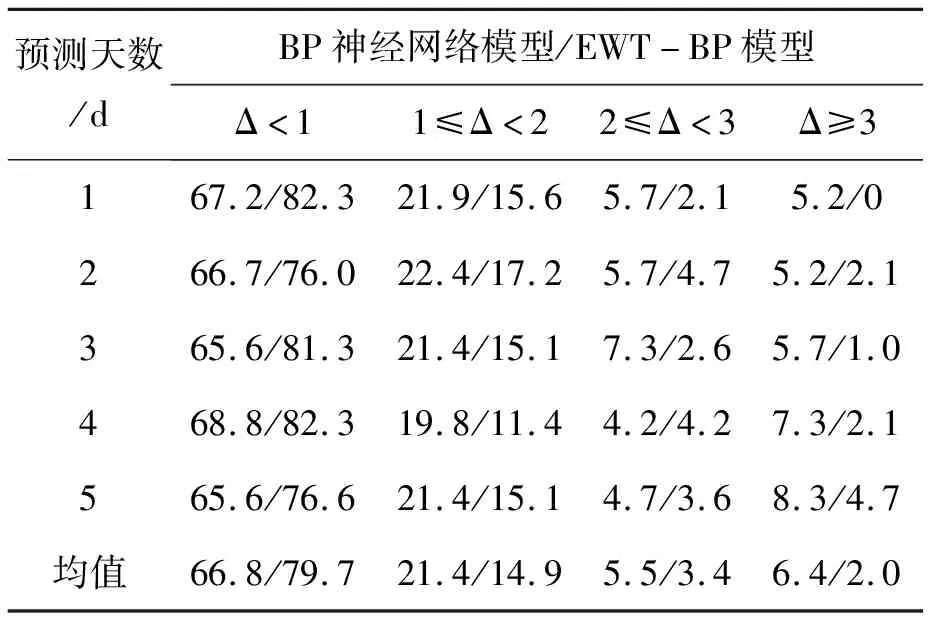
表1 BP模型和EWT-BP模型的殘差絕對值Δ(以TECU為單位計數)分類百分比/%

表2給出了不同地理位置的誤差情況對比表。從表2中可以看出，同一地理位置，EWT-BP模型預測的相對精度普遍要比單一BP模型的相對精度要高，均方根誤差普遍比單一BP模型的均方根誤差要小，結果表明經驗小波神經網絡的預測效果要優于單一神經網絡的預測效果。同一經度，均方根誤差隨著緯度的增加而減小，相對精度則未體現相同的變化趨勢，其與不同位置處的TEC值大小相關。同一緯度不同經度間誤差變化不明顯。

表2 不同地理位置5 d內平均預測誤差情況對比表

表3為4個時段誤差情況對比表，表3中顯示BP模型預測的平均相對精度為90.2%，均方根誤差為1.3；而EWT-BP模型預測的平均相對精度為93.2%，均方根誤差為0.83。整體結果表明，EWT-BP模型的預測效果優于單一BP模型的預測效果。

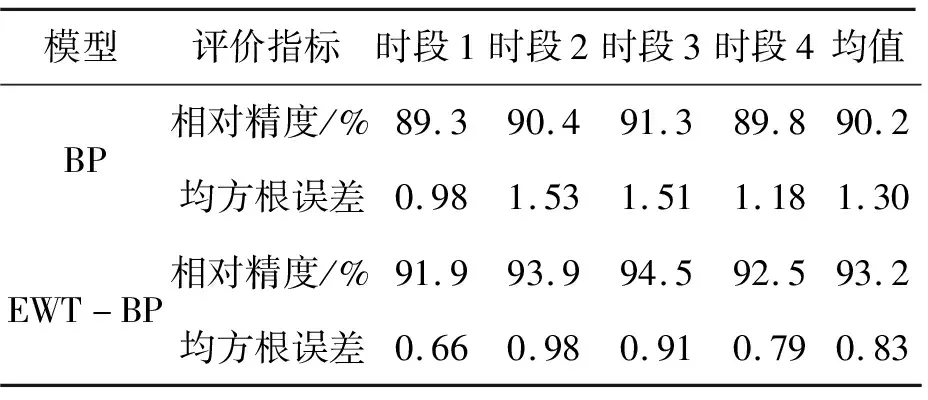
表3 4個時段平均預測誤差情況對比表

3 結論

采用IGS中心提供的電離層格網數據進行實驗，驗證了EWT-BP神經網絡模型預測的有效性，并與單一BP模型預測效果進行對比分析得出以下結論。

1)利用EWT對電離層TEC時間序列數據進行分解，對分解的各分量進行BP預測，預測結果疊加得到最終TEC值，并與TEC真實值進行對比。結果表明，EWT-BP預測模型能夠有效地反映電離層TEC的變化特征。

2)對比單一神經網絡模型的預測結果，組合模型預測的平均相對精度提高了3%，均方根誤差減小了0.47，表明組合模型的預測效果更優。

本文將經驗小波變換運用到非線性時間序列當中，給類似特征的時間序列預測提供了一個新思路。但是電離層復雜多變的時空特性給模型預測帶來一定困難，此外神經網絡預測模型主觀性強的缺點也有待進一步解決。建立一個預測精度更高，穩定性更強的電離層預測模型還有待進一步的研究。

致謝：感謝IGS中心提供的電離層TEC數據！