基于MIMO的可見光通信技術(shù)性能研究

蔣 岑

（湖北工業(yè)大學(xué) 工程技術(shù)學(xué)院，湖北 武漢 430068）

0 引 言

光通信技術(shù)已經(jīng)成為全球無線通信產(chǎn)業(yè)的主要發(fā)展趨勢之一。本文將在簡要介紹3種基于MIMO的可見光通信系統(tǒng)上，結(jié)合兩種類型的白光LED特性分析其各自的優(yōu)缺點，重點針對非成像和成像MIMO系統(tǒng)中需要考慮的光源布局進行仿真驗證分析[1]。

1 基于MIMO的可見光通信系統(tǒng)

現(xiàn)階段基于MIMO的可見光通信系統(tǒng)主要有3種。第一種，像素化MIMO可見光通信系統(tǒng)，即點到點的MIMO光信道。它使用二維光發(fā)射器陣列形成編碼成像序列來傳輸高速率數(shù)據(jù)，利用成像檢測器檢測圖像。在一個典型的像素化MIMO可見光通信系統(tǒng)模型中，發(fā)射器是空間光調(diào)制器，用于產(chǎn)生被電域?qū)ぶ房刂频妮敵龉鈴姸瓤臻g分布。發(fā)射器陣列包括LED陣列、液晶顯示器、垂直腔面發(fā)射激光器以及有機聚合物LED等。第二種，非成像MIMO可見光通信系統(tǒng)有Nr個LED發(fā)射器和Ng個接收器，來自每個LED的光信號發(fā)射并行獨立的數(shù)據(jù)流，且都被獨立接收器接收（強度有所差異），而檢測器陣列中的多個像素點為獨立接收單元。第三種，成像MIMO可見光通信系統(tǒng)。使用非成像單元實現(xiàn)角度分集，需要每個接收單元采用分離的光學(xué)集中器，成本較高且笨重，而使用棱鏡的角度分集接收機則具有明顯的優(yōu)勢。一方面，一個聚光器被所有光電檢測器所共享，大幅降低了設(shè)計尺寸和成本。另一方面，所有光電檢測器可以放置在單個平面陣列上，用于大量接收單元或像素的使用[2]。

2 基于MIMO的可見光通信系統(tǒng)的光源布局

在可見光通信系統(tǒng)中，光源具有通信和照明的雙重作用。由于照明通常需要布置多個LED燈，因此光源布局將極大影響系統(tǒng)的性能。不同的光源布局勢必會導(dǎo)致室內(nèi)光功率分布的不同，必須合理布置光源使室內(nèi)光功率的分布趨向均勻。本文簡要探討了非成像和成像MIMO可見光通信系統(tǒng)中的光源布局問題。

2.1 LED光源布局分析

發(fā)光強度和發(fā)射功率是LED的兩個基本參數(shù)。

發(fā)光強度用朗伯輻射模型可表示為：

式中，θ為LED輻射角；m為朗伯輻射的階數(shù)。

光照強度可表示為I(θ)=I0cosmθ，水平方向上點(x,y,h)處的照度可表示為：

式中，I0為LED的中心照度；φ為入射角；d為接收器的LED間的距離[3]。

設(shè)定房間大小為7.8 m×6.0 m×3.0 m，6個LED光源距離地面的高度為3 m，放置接收器的桌子高度為0.8 m，每個光源的光通量為3 600 lm，發(fā)送功率為36 W。屋頂、墻壁以及地板的反射系數(shù)分別為0.2、0.8以及0.7，如表1所示。

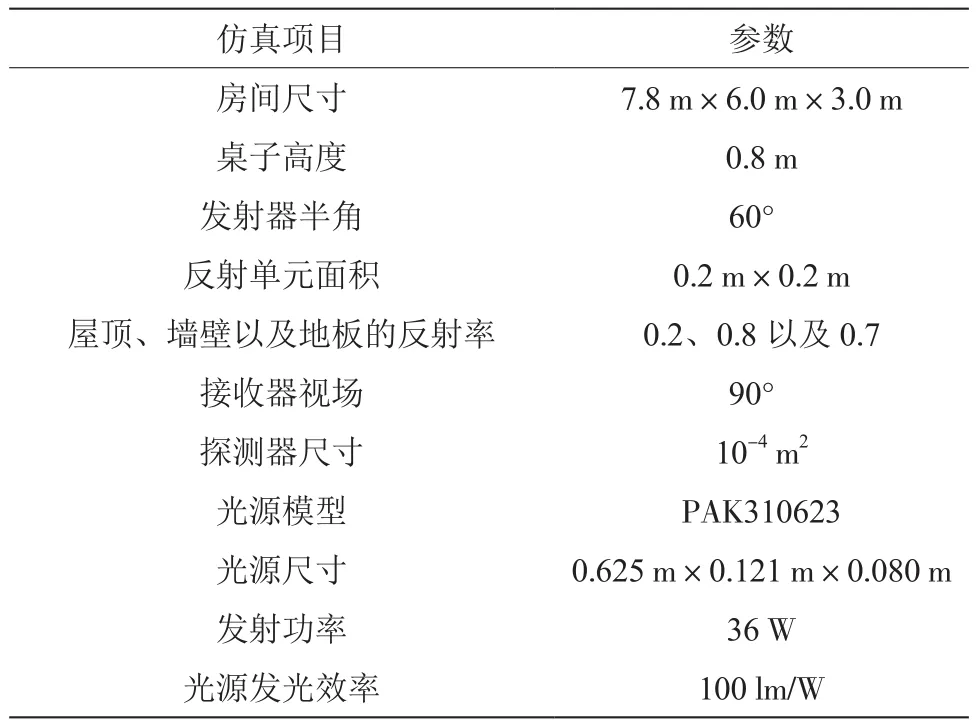
表1 仿真系數(shù)

設(shè)X-Y平面與地面平行，Z軸為垂直方向。6個LED光源的中心位置分別為（2.1，1.8，3）、（2.1，4.2，3）、（3.9，1.8，3）、（3.9，4.2，3）、（5.7，1.8，3）以及（5.7，4.2，3），即原始布局。為確保仿真結(jié)果的準確性，考慮LED光源的尺寸，設(shè)其為0.625 m×0.121 m×0.080 m。

在原始布局中，6個LED光源主要集中在房間中心區(qū)域，將導(dǎo)致中心區(qū)域亮度較高而靠墻的區(qū)域亮度較低，均勻性較差。房間內(nèi)光照強度的均勻性定義為：

式中，Emin為最小光照強度；Eave為高度0.8 m的接收平面上的平均光照強度[4]。

原始布局下照度分布如圖1所示，其中最大照度和最小照度分別為475 lx和186 lx，其均勻性為0.55。角落里的光照強度比中心處的光照強度低了60.8%，顯然任意布局下的光照均勻性不夠好。

圖1 原始布局下的照度分布

點(x,y,h)處的照度為：

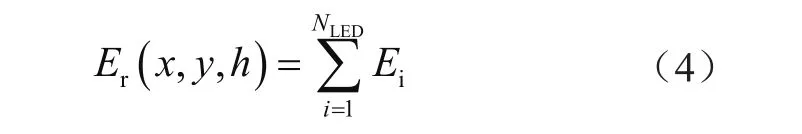
式中，Ei為一個LED的照度。經(jīng)計算總反射率為4.84%，其中第一級反射占了3.57%。隨著反射次數(shù)的增加，反射效果h顯著衰減，因此布局優(yōu)化時僅考慮第一級反射。設(shè)光源、接收器以及反射器單元的數(shù)目分別為t、r以及n，根據(jù)MIMO系統(tǒng)模型，接收平面上的照度為：

式中，P為光源的光功率；η為光源的發(fā)光功率；Dt×r為光源從接收器的直射路徑對應(yīng)系數(shù)；Et×n為光源和反射單元間的傳遞函數(shù)；Mn×r為反射單元和接收器間的傳遞函數(shù)；Et×nMn×r為第一級反射對應(yīng)的系數(shù)。

為計算通過反射產(chǎn)生的照度，先考慮一個反射率為ρ的微分反射單元dA，視其為一個面積為dA的接收器以計算其收到的照度，然后視其為一個服從朗伯輻射模型的光源，計算其發(fā)射強度。顯然，反射單元的面積越小和數(shù)目越多，仿真結(jié)果越精確。但是，考慮到小面積大數(shù)目所帶來的高計算復(fù)雜度，有必要選擇合適面積和數(shù)目的反射單元以權(quán)衡計算精度和計算復(fù)雜度。對于一個尺寸為L×W×H的房間，相關(guān)研究中給出了反射單元的數(shù)目，為：

式中，d為相鄰單元的中心間距，下文中d為0.2 m。考慮到接收器放置在桌子上，高度低于桌子的反射單元可以視為無效，僅計算高于桌子的反射單元，因此可將式（6）改為：

式中，h為接收平面的高度，下文取h為0.8 m。由于反射單元直接接收光源發(fā)射的光線，因此有：

式中，cos(θij)等于兩個向量的點積，第一個垂直于光源i，第二個從光源i發(fā)出并指向反射單元j；φij為垂直于反射單元j的向量和連續(xù)光源i及反射單元j的向量間的夾角；dij為光源i到反射單元j的距離。

傳遞函數(shù)為：

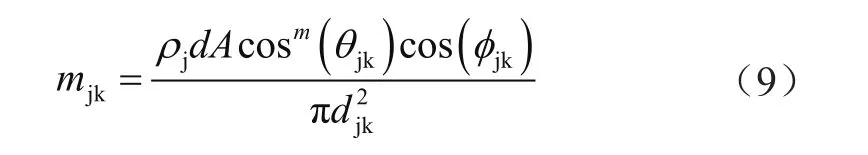
式中，ρj為反射單元的反射系數(shù)；dA為反射單元j的面積；θjk為第j個反射單元的法向量和從第j個反射單元指向第k個接收器的向量間的夾角；φjk為第k個反射單元的法向量和從第k個反射單元指向第j個接收器的向量間的夾角；djk為第j個反射單元和第k個接收器間的距離。

在3個矩陣確定后，可以計算出來接收平面上的光照度。為評價布局的優(yōu)劣，定義光照強度的方差為：

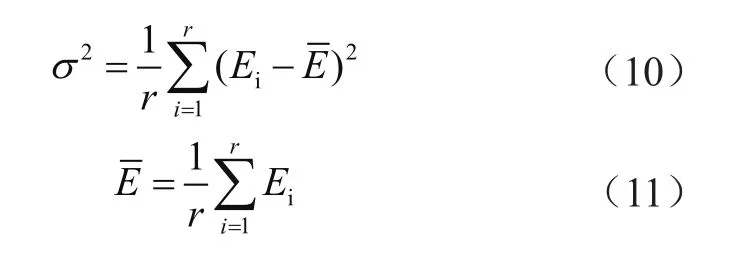
式中，r為接收平面上的接收器數(shù)目；Ei為第i個接收器接收到的光照強度；為平均光照強度。顯然，方差越小，表明光照強度分布越均勻。美觀起見，仍保持光源關(guān)于房間中心對稱，如圖2所示。如果第一個光源的坐標為（x0，y0，3），則其他光源的坐標為（x0，6-y0，3）、（3.9，y0，3）、（3.9，6-y0，3）、（7.8-x0，y0，3）以及（7.8-x0，6-y0，3）。仿真中，t為6，接收平面上分布著26×20個接收器，x0和y0的變化范圍均為0～2。仿真發(fā)現(xiàn)，當x0為0.7 m、y0為1.2 m時，方差最小，即當x0為0.7 m、y0為1.2 m時布局最優(yōu)。可以看出，光源不再集中在房間中心的一個小區(qū)域內(nèi)，而是更靠近墻壁。本文參考了LED光源室內(nèi)布局的相關(guān)研究，簡要分析了光源布局對照度的影響，對在6.0 m×7.8 m的房間中2×3的光源進行對稱分布。按照表1設(shè)定環(huán)境中的各參數(shù)，按照相關(guān)研究中的優(yōu)化方法，以光照度為評判基準優(yōu)化光源布局，得到如圖2所示的優(yōu)化布局[5]。

圖2 優(yōu)化布局

2.2 仿真結(jié)果

從仿真結(jié)果可知，原始布局光照度的范圍為186～475 lx，優(yōu)化布局下光照度的范圍為266～363 lx。優(yōu)化布局下，光照度的最大值出現(xiàn)在每個光源的下方而非房間的中心，原因是光源不再集中于房間的小范圍內(nèi)，而是更加靠近墻壁，縮小了光源和接收器間的距離，使得靠近墻壁的接收器能夠接收更多的光，從而減小了光照度的波動。可見，優(yōu)化后的布局能得到更加均勻的光照度，從而降低接收器接收到的光強與接收器在房間中位置的關(guān)聯(lián)性。

3 結(jié) 論

本文從MIMO技術(shù)出發(fā)，在基于MIMO的可見光通信系統(tǒng)模型上，探討了LED光源布局對基于MIMO的可見光通信系統(tǒng)性能的影響，并以光照度為衡量標準對光源布局進行修改，得到了優(yōu)化布局結(jié)果。仿真結(jié)果表明，優(yōu)化布局的光照度相比任意選擇布局的光照度均勻性更好，更適用于照明和通信。本文僅說明了2×3對稱布局的情形，并未推廣到一般情況，因此下一步有必要深入分析在非長方體房間中非對稱的光源布局。