8 MHz射頻容性等離子體的功率沉積和電子密度模擬

李丙宏

（朔州師范高等專科學校 自然科學系，山西 朔州 036002）

0 引 言

容性射頻等離子源由等離子體和射頻源構成。所謂等離子體，是指物質存在的一種特殊狀態，其內部有電子、陰離子、陽離子以及中性粒子。它不屬于固體和液體，也不屬于氣體，是一種宏觀上保持電中性的第四狀態。射頻源，即提供相應能量和電磁波的設備。射頻源對等離子體的研究具有非常重要的作用。

容性射頻等離子體，在微電子和集成電路產業中有著極其重要的應用[1]，尤其在芯片刻蝕工藝中起到了決定性作用。在精細刻蝕工藝中，往往需要在幾個原子的厚度下完成，同時對電壓和溫度的控制也是一個極大的挑戰。另外，刻蝕效果與等離子體密切相關，功率沉積和電子密度是反映等離子體性能的指標。

圖1為射頻容性耦合等離子體放電結構。它的特點是其鞘層中的位移電流可以使等離子體能夠在較低功率下穩定而連續地放電[2]。該結構主要由電極、等離子體、放電腔體以及射頻源組成。兩極板平行放置，一端施加特定的電壓，另一端接地。在等離子區，電子主要以電熱的方式獲得能量。在金屬鞘區域，由于此處的電磁環境相比內部要復雜得多，因此能量變化是隨機的[3]。

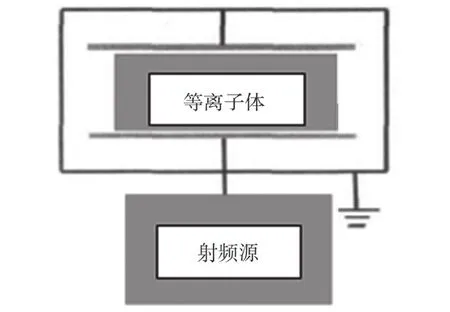
圖1 射頻等離子源結構

1 建模及基本設定

如圖2所示，假定等離子體的體積足夠，在等離子體的內部任意區間取0.025 m和0.01 m的直線（實際上，它是弧線的一段，只要邊界條件設置合適，并不影響對問題的研究），AB=0.025 m，BC=0.01 m。

圖2 模型線

對AB段進行有限元分割，弧長表示為：

對于全局等離子體部分的中性物質，令w為廣義功率，則沉積功率滿足：

對等離子體部分的離子，滿足方程：

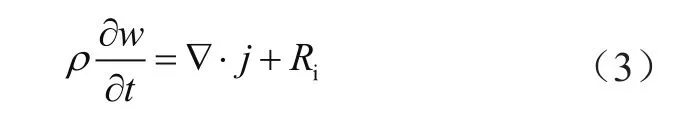
式中，Ri為第i個微元的電阻；j滿足j=ρwVd，E為電場強度矢量，而Vd滿足：

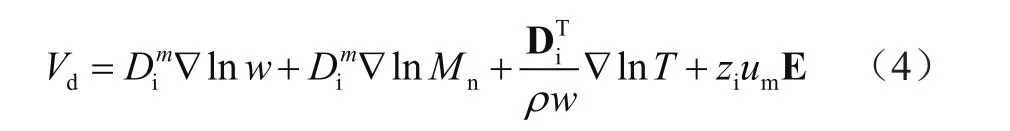
不可否認，無論什么材料都不可能不產生震動，因此形函數采用拉格朗日函數的線性部分，去掉微小擾動項。

邊界點A、B、C仍舊可以用式（1）描述，但局部等離子體的波數符合統計規律：

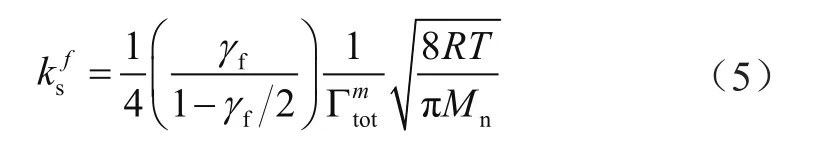
式中，γ為可獲得的協調參數。

2 模型滿足的方程

2.1 模型的AB段滿 足的方程

AB段的空間電子通量滿足：

式中，μe為電子電場遷移率；E為電場強度矢量；ne為電子數密度；De為電子擴散系數。

AB段滿足的偏微分方程為：

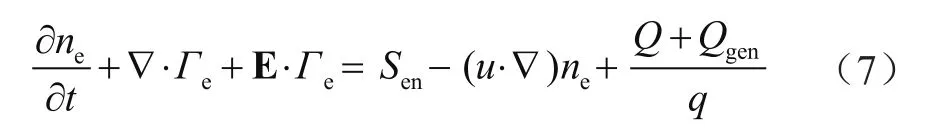
式中，Sen為碰撞過程電子能對局部等離子體密度的貢獻；u和Qgen為狀態函數。

就BC段而言，只要滿足電位移矢量和電場強度矢量的本構關系即可。

2.2 全局方程

對于全局問題的電磁學表述，采用麥克斯韋方程的變形微分形式：

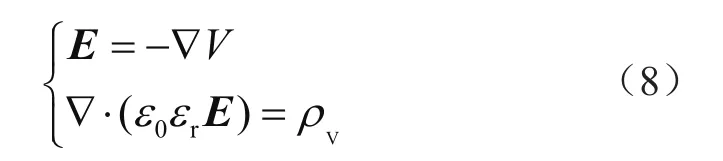
式中，ρV是全局體積密度。電位移與電子密度滿足-n·D=0，同時Γ滿足-n·Γe=0。初始電子密度（單位體積的電子個數）為1×1013個/m3。電子能閾值等于1且無弱項約束，這樣邊界點B上有：

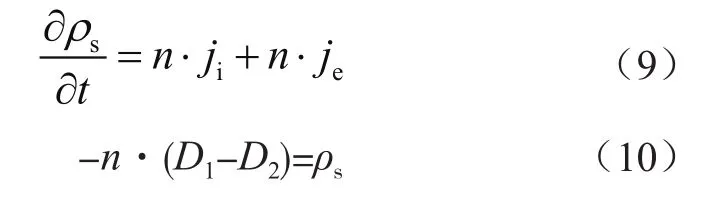
式中，A點的電勢為0，C點電勢為V0=220 V。

3 結果與討論

經仿真模擬，以Ar參與反應的等離子體為工作物質，工作電壓為220 V，射頻源頻率為8 MHz，壓強為133.32 Pa，研究射頻等離子體的功率沉積和電子密度。

3.1 功率沉積

圖3中，隨著弧長的延長，不同相位的電磁波驅動的等離子體功率沉積方向不同，部分向負向沉積，部分向正向沉積。在0.007 5 m處，正向功率沉積第一次達到峰值；在0.017 5 m附近處，正向功率沉積第二次達到峰值；正向功率沉積整體呈馬鞍狀分布。在0.008 5 m附近，負向功率沉積第一次達到峰值；0.017 m附近，負向功率沉積第二次達到峰值；負向功率沉積整體分布與正向功率沉積的分布接近，但方向與之相反。所有的功率沉積在0.012 5 m附近功率沉積的值最小，因此此處的數值為功率沉積的最小閾值。

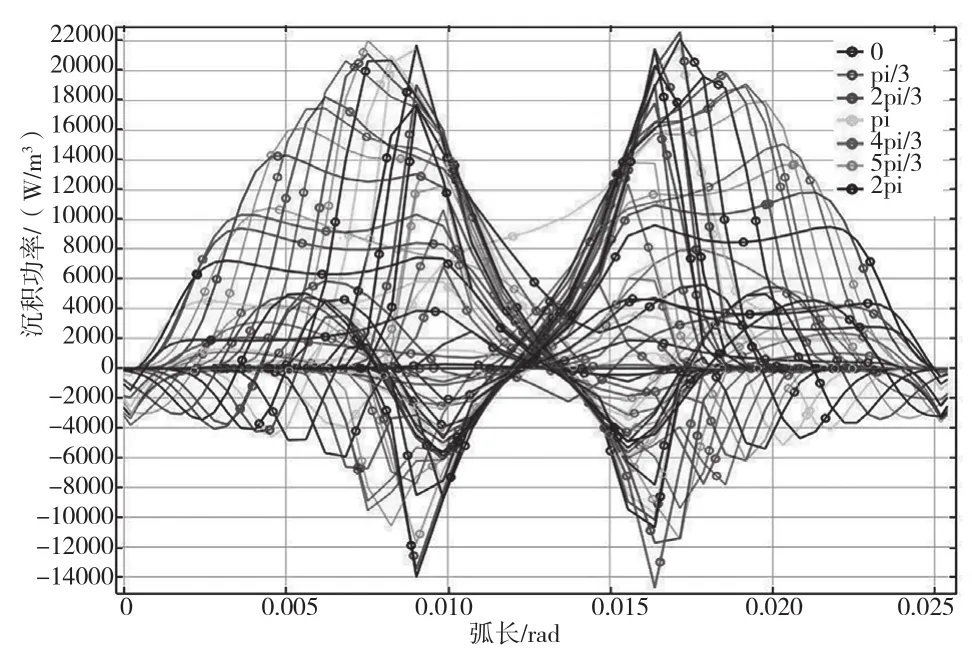
圖3 功率沉積

3.2 電子密度

如圖4所示，在起始位置附近，電子密度達到了一個峰值，后電子密度驟減，電子密度以近似波浪線的方式衰減，直至0.075 m左右達到最小閾值，且保持至0.016 m附近。從約0.016 m開始，電子密度又以近似波浪線的形式開始增大，直到終端位置才重新達到了峰值。因此，在中間區域即等離子體區域，電子密度會達到一個相對穩定的水平，而在極板附近會形成峰值，可見載流子在單位電場中的遷移速率在極板附近是最快的。就走勢而言，電子密度的變化基本與離子密度的變化呈反向關系，即離子密度升高時對應的電子密度會降低，離子密度降低時電子密度會升高。

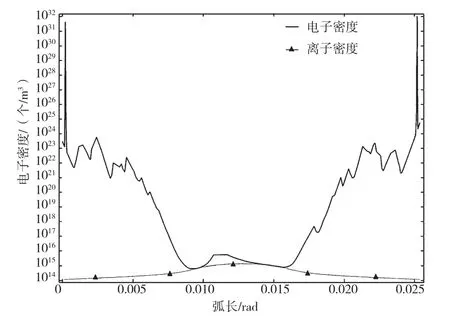
圖4 電子密度變化圖

4 結 論

本文通過有限元法對8 MHz射頻容性等離子體在133.32 Pa壓強下經220 V的低電壓驅動的條件，模擬了其功率沉積和電子密度的變化情況。8 MHz射頻容性等離子體的功率沉積主要集中在等離子體部分，電子密度分布主要集中在極板附近。與常見的13.56 MHz的射頻容性等離子體源相比較，它們的性能基本一致。