非平穩信道下LDPC碼低復雜度滑窗置信傳播聯合信道估計與譯碼算法
楊 洋 方 勇 單博煒
(長安大學信息工程學院 西安 710064)
1 引言
由于移動通信系統對高吞吐率的需求不斷增長,具備高譯碼并行度的LDPC碼取代了Turbo碼被第5代移動通信技術標準(5G New Radio, 5G NR)所采用。此外,與Turbo碼相比,LDPC碼還具有更高的編碼增益,更高的譯碼運算效率,以及更低的錯誤平層等優勢[1],并將繼續成為下一代移動通信技術標準中信道編碼方案的有力競爭者。
自5G NR開始,移動通信系統需支持更多新應用場景下的可靠通信,特別是高速移動場景,例如高速鐵路、車載自組織網絡(Vehicular Ad hoc NETworks, VANETs)、無人機(Unmanned Aerial Vehicles, UAVs)等。在高速移動場景下,信道呈現時變的非平穩特性,這給信道估計帶來很大挑戰,因為過大的信道估計誤差會導致LDPC碼置信傳播(Belief-Propagation, BP)譯碼的性能惡化[2]。
常用的信道估計方法可根據是否依賴導頻信號分為兩類。一類是基于導頻輔助的方法,包括最小二乘估計、最小均方誤差估計和最大似然估計等。采用連續消除類譯碼算法[3,4]的極化碼常采用此類信道估計方法[5]。然而在非平穩信道條件下,若要利用基于導頻輔助的方法準確追蹤時變的信道狀態將導致大量的導頻開銷,從而降低傳輸效率。另一類是不需要或僅需要極少量導頻輔助,主要發掘接收信號本身所蘊含信道信息的盲信道估計方法,這類方法更適合非平穩信道條件下的信道估計。文獻[6]針對極化碼提出一種可輸出軟信息的連續消除列表譯碼算法, 并通過盲信道估計與信道譯碼之間的迭代實現聯合信道估計與譯碼(Joint Channel Estimation and Decoding, JCED)。LDPC碼的BP譯碼本身就是可輸出軟信息的迭代譯碼算法,因此也可實現JCED:文獻[7]將基于重要性重采樣的盲信道估計與BP譯碼相結合,文獻[8]將基于粒子濾波的盲信道估計與BP譯碼相結合來實現JCED。當然,也存在不與BP譯碼相結合的盲信道估計,例如文獻[9]提出的基于最大熵定理的盲信道估計方法。此外,若譯碼器不需要信道信息,則不必進行信道估計,稱為非相干傳輸[10]。文獻[11,12]實質上提出一種需借助極少量導頻符號來初始化列表譯碼器的非相干傳輸方案,主要適用于極短碼。文獻[13]提出的基于深度學習和字典學習的LDPC碼譯碼方案,將譯碼問題轉化為圖像去噪問題處理,不存在信道估計過程,因此也可看作一種非相干傳輸方案。
在5G移動通信系統中,即使在sub-6 GHz頻段,若相對移動速度達到300 km/h,所帶來的多普勒擴展也足以導致信道狀態在103bit的傳輸時間內發生變化。也就是說,若碼長超過103,則在1個碼字的傳輸時間內會經歷不同的信道狀態。然而現有文獻在解決非平穩信道條件下的信道估計問題時,大多假定信道狀態在同一碼字的傳輸時間內保持不變[7,9]。文獻[8,13]提出的方法雖無此假定,但無論是粒子濾波還是深度學習,在應用時都面臨計算復雜度過高的問題。為解決高速移動場景下的信道估計與譯碼問題,本文基于信源編碼中用于信源參數估計和信源相關性估計的滑窗置信傳播(Sliding-Window Belief-Propagation, SWBP)算法[14,15],提出一種非平穩信道下LDPC碼的JCED算法,同時提出兩種低復雜度的自適應滑窗長度設置方法。通過對不同碼長、不同碼率、規則與非規則LDPC碼的仿真,全面評估所提算法的性能。另外,還對所提算法的初值敏感性和錯誤平層等問題進行研究。
2 基于SWBP的JCED算法
SWBP是處理信源編碼中非平穩信源的參數估計問題[14]以及信源之間的非平穩相關性估計問題[15]的有效方法。本節將該方法進行擴展,用來解決非平穩信道下LDPC碼的聯合信道估計與譯碼問題,提出基于SWBP的JCED算法。并對信道估計時計算復雜度較高的關鍵步驟-自適應滑窗長度設置問題進行研究,提出兩種低復雜度的自適應滑窗長度設置方法。
2.1 信道模型和符號說明


T 表示所設定的最大JCED迭代次數。
2.2 基于SWBP的JCED算法


2.3 基于滑窗的信道估計算法




3 仿真結果與分析
本節中,將利用不同碼長、不同碼率、規則與非規則LDPC碼對所提基于SWBP的JCED算法進行全面的評估。為排除不同碼結構對性能的影響,專注于評估JCED算法本身,仿真用到的規則碼均采用漸近邊增長(Progressive Edge Growth, PEG)算法構造;為了兼顧檢驗錯誤平層,仿真用到的非規則碼采用CCSDS標準[16]中官方驗證過錯誤平層性能的AR4JA碼。


3.1 (1024, 3, 6) LDPC碼的仿真
在本小節中,利用碼長較短、碼率適中的(1024,3, 6)碼完成平方搜索交叉熵滑窗長度設置方法的有效性驗證;完成基于多種滑窗長度設置方法的JCED算法的相對時間復雜度比較;完成基于DFT滑窗長度設置方法的JCED算法對局部噪聲方差初始估計值的敏感性驗證;對基于多種滑窗長度設置方法的JCED算法的BER性能、平均迭代次數做初步評估。
圖1給出了基于多種滑窗長度設置方法的JCED算法的BER性能曲線。由圖中可知:基于平方搜索交叉熵滑窗長度設置方法的JCED算法性能與基于全搜索交叉熵滑窗長度設置方法的JCED算法性能幾乎相同,考慮到平方搜索相對于全搜索在計算效率上的巨大提升,在隨后的仿真中,交叉熵滑窗長度設置方法均采用平方搜索的實現方式;另外,基于DFT滑窗長度設置方法的JCED算法性能與基于交叉熵滑窗長度設置方法的JCED算法性能幾乎相同,在BER= 10?5時,與理想估計(即已知局部噪聲方差)條件下的BP譯碼算法相比僅有0.25 dB的性能差距,而與僅已知局部噪聲方差的均值的BP譯碼算法相比可獲得1.2 dB的性能增益。
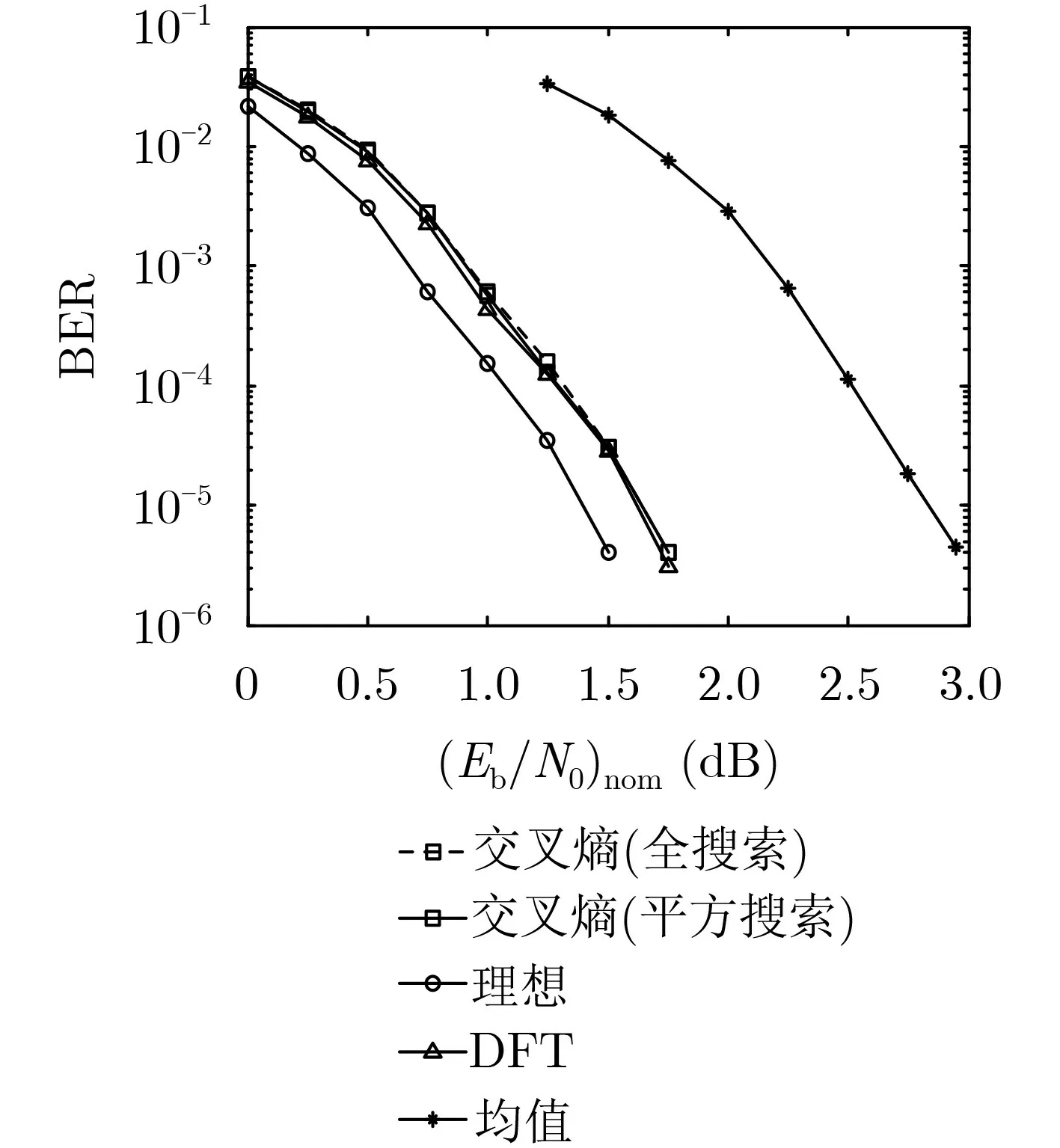
圖1 多種滑窗長度設置方法下的算法BER性能
圖2給出了基于多種滑窗長度設置方法的JCED算法的平均迭代次數曲線。由圖中可知:基于DFT滑窗長度設置方法的JCED算法的平均迭代次數與基于交叉熵滑窗長度設置方法的JCED算法的平均迭代次數幾乎相同,在BER= 10?5時,僅比理想估計條件下的BP譯碼算法的平均迭代次數多5%~6%。
圖3給出了基于多種滑窗長度設置方法的JCED算法單輪迭代的相對時間復雜度。計算方法是:在仿真中不設置迭代中止條件,使1幀數據在相應JCED算法下持續迭代105輪并記錄運行時間,該運行時間除以1幀數據在BP譯碼算法下持續迭代105輪的運行時間所得的商即為相應JCED算法的相對時間復雜度。該指標可直觀反映JCED算法單輪迭代的計算復雜度。由圖中可知,基于全搜索交叉熵滑窗長度設置方法的JCED算法的計算復雜度是不可接受的;采用平方搜索后,計算復雜度下降巨大,但信道估計部分的計算復雜度(355%-100%=255%)仍然超過譯碼部分(100%);而基于DFT滑窗長度設置方法的JCED算法,其信道估計部分的計算復雜度(122%-100%=22%)僅為譯碼部分(100%)的22%,考慮其帶來的性能增益,計算復雜度的提升程度是完全可以接受的。
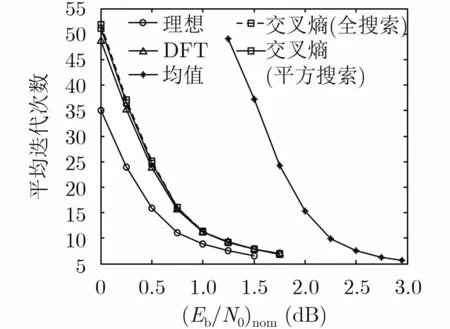
圖2 多種滑窗長度設置方法下的算法平均迭代次數
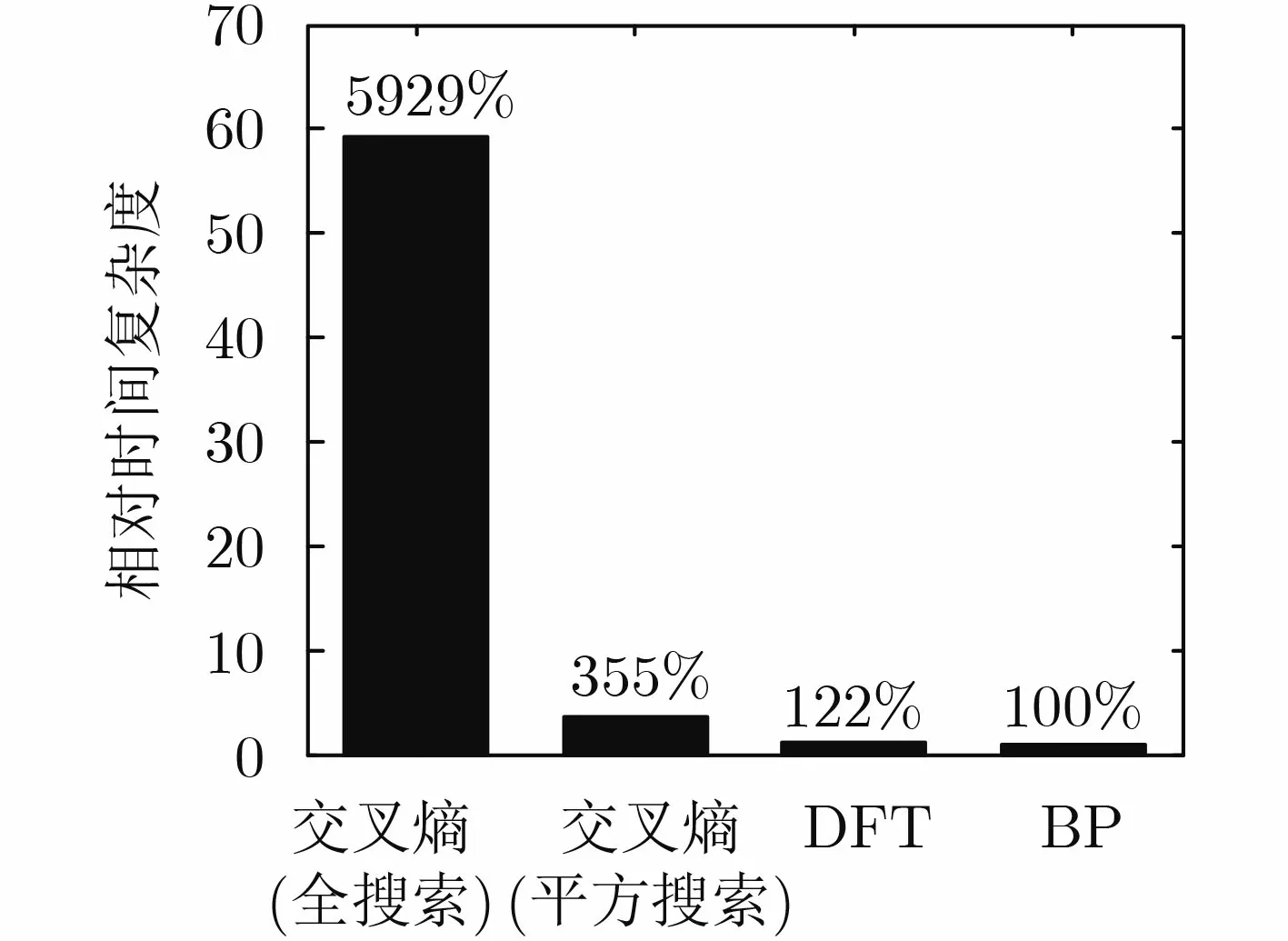
圖3 多種滑窗長度設置方法下的算法相對時間復雜度
圖4給出了不同局部噪聲方差初始估計值下,基于DFT滑窗長度設置方法的JCED算法的BER性能。由圖中可知,即使( Eb/N0)nom失 配達到±10lg4=±6 dB,對BER性能也幾乎沒有影響,說明基于DFT滑窗長度設置方法的JCED算法有著很強的魯棒性。基于交叉熵滑窗長度設置方法的JCED算法也有類似的結論,這里不再贅述。
圖5給出了不同局部噪聲方差初始估計值下,基于DFT滑窗長度設置方法的JCED算法的平均迭代次數,由圖中可知,與BER性能不同,平均迭代次數對 (Eb/N0)nom失配是敏感的:在BER=10?5時,若失配3 dB,則平均迭代次數增加41%,若失配6 dB,則平均迭代次數增加69%;若失配-3 dB,則平均迭代次數增加15%,若失配-6 dB,則平均迭代次數增加32%。總之,失配程度越高,平均迭代次數增加越多;相同失配程度下,低估 σˉ2(即失配為正值)比高估σ ˉ2(即失配為負值)會導致平均迭代次數更多地增加。更多的平均迭代次數意味著更高的時延、更低的吞吐量、更大的能耗。因此,若條件允許,應盡量保證 σˉ2的估計精度,特別是對時延、吞吐量及能耗敏感的應用,尤其應盡量避免低估 σˉ2。基于交叉熵滑窗長度設置方法的JCED算法也有類似的結論,這里不再贅述。

圖4 不同局部噪聲方差初始估計值下的算法BER性能
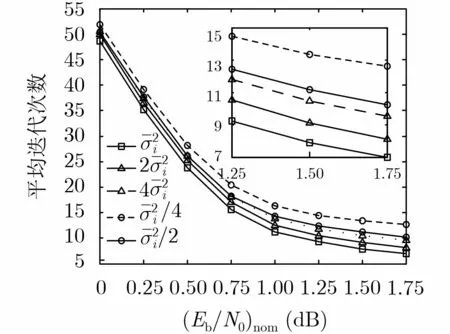
圖5 不同局部噪聲方差初始估計值下的算法平均迭代次數
3.2 不同碼長、不同碼率、規則與非規則LDPC碼的仿真
在5G NR[1,17]中,由于需要滿足多樣的業務需求和應對多變的傳輸環境,所采用的LDPC碼的碼長、碼率跨度非常大。下一代移動通信同樣需要很大的碼長、碼率變化范圍。因此,有必要對不同碼長、不同碼率、規則與非規則的LDPC碼在所提基于SWBP的JCED算法下的性能做全面的評估。
3.2.1 不同碼長LDPC碼的仿真
圖6給出了(8192, 3, 6)碼在基于兩種滑窗長度設置方法的JCED算法下的BER性能曲線。作為對比,同時給出了圖1所示(1024, 3, 6)碼的BER性能曲線。由圖中可知,在不同碼長下基于交叉熵滑窗長度設置方法和基于DFT滑窗長度設置方法的JCED算法有著幾乎相同的BER性能;(8192, 3,6)碼在BER= 10?5時,JCED算法與理想估計條件下的BP譯碼算法相比僅有不足0.1 dB的性能差距,而與僅已知局部噪聲方差的均值的BP譯碼算法相比可獲得1.4 dB的性能增益。與(1024, 3, 6)碼的結果對比可知,在給定的BER下,相同碼率的LDPC碼,碼長越長,JCED算法與理想估計條件下BP譯碼算法的性能差距越小,與僅已知局部噪聲方差的均值的BP譯碼算法相比性能增益也越大,但總體而言兩者隨碼長變化的趨勢不明顯。
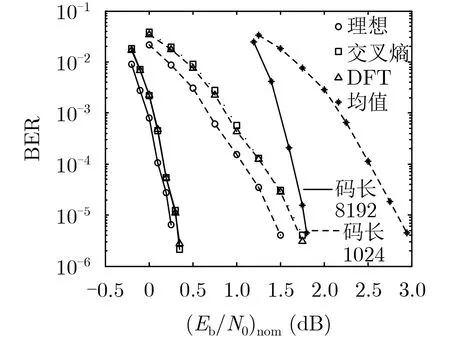
圖6 相同碼率,不同碼長的碼在所提JCED算法下的BER性能
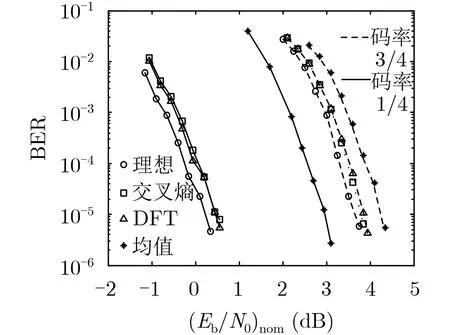
圖7 相同碼長,不同碼率的碼在所提JCED算法下的BER性能
3.2.2 不同碼率LDPC碼的仿真
圖7給出了碼率分別為 1/4 和3 /4的(1024, 3,4)碼和(1024, 3, 12)碼在基于兩種滑窗長度設置方法的JCED算法下的BER性能曲線,再結合圖1所示(1024, 3, 6)碼的BER性能曲線,可以看到:在不同碼率下,基于兩種滑窗長度設置方法的JCED算法有著幾乎相同的BER性能;(1024, 3, 4)碼、(1024, 3, 6)碼和(1024, 3, 12)碼在BER= 10?5時,JCED算法與理想估計條件下的BP譯碼算法相比均只有0.15~0.25 dB的性能差距,而與僅已知局部噪聲方差的均值的BP譯碼算法相比可分別獲得2.4 dB, 1.2 dB和0.4 dB的性能增益。因此,JCED算法相對于僅已知局部噪聲方差均值的BP譯碼算法的性能增益隨碼率變化的趨勢非常明顯,JCED算法更適合提升中低碼率的碼在非平穩信道下的BER性能。
3.2.3 規則與非規則LDPC碼的仿真
圖8給出了碼長、碼率均相同的(2048,3,6)規則碼與CCSDS標準中的AR4JA非規則碼在基于兩種滑窗長度設置方法的JCED算法下的BER性能曲線。由圖中可知,無論對于規則碼還是非規則碼,基于兩種滑窗長度設置方法的JCED算法有著幾乎相同的BER性能;在平穩信道下性能優異的非規則碼,在非平穩信道下依然保持著對規則碼的性能優勢;非規則碼在BER= 10?5時,JCED算法與理想估計條件下的BP譯碼算法相比均只有0.2 dB的性能差距,而與僅已知局部噪聲方差的均值的BP譯碼算法相比可獲得1.5 dB的性能增益,規則碼也有相同的結論。因此,JCED算法對規則碼與非規則碼同樣適用,沒有明顯的性能傾向。
圖9給出了CCSDS標準中的AR4JA非規則碼在基于兩種滑窗長度設置方法的JCED算法下的錯誤平層驗證曲線。錯誤平層產生的原因有兩種,可能是碼結構本身造成的,也可能是譯碼算法或譯碼算法的實現細節造成的。該碼具有良好的最小距離特性,且在平穩信道下已通過官方FPGA平臺驗證在BER= 10?8下不存在錯誤平層,因此排除了碼結構本身導致錯誤平層的可能,能夠用來檢驗JCED算法是否會導致錯誤平層。由圖中可知,在BER=10?8下,基于兩種滑窗長度設置方法的JCED算法均不會導致錯誤平層。
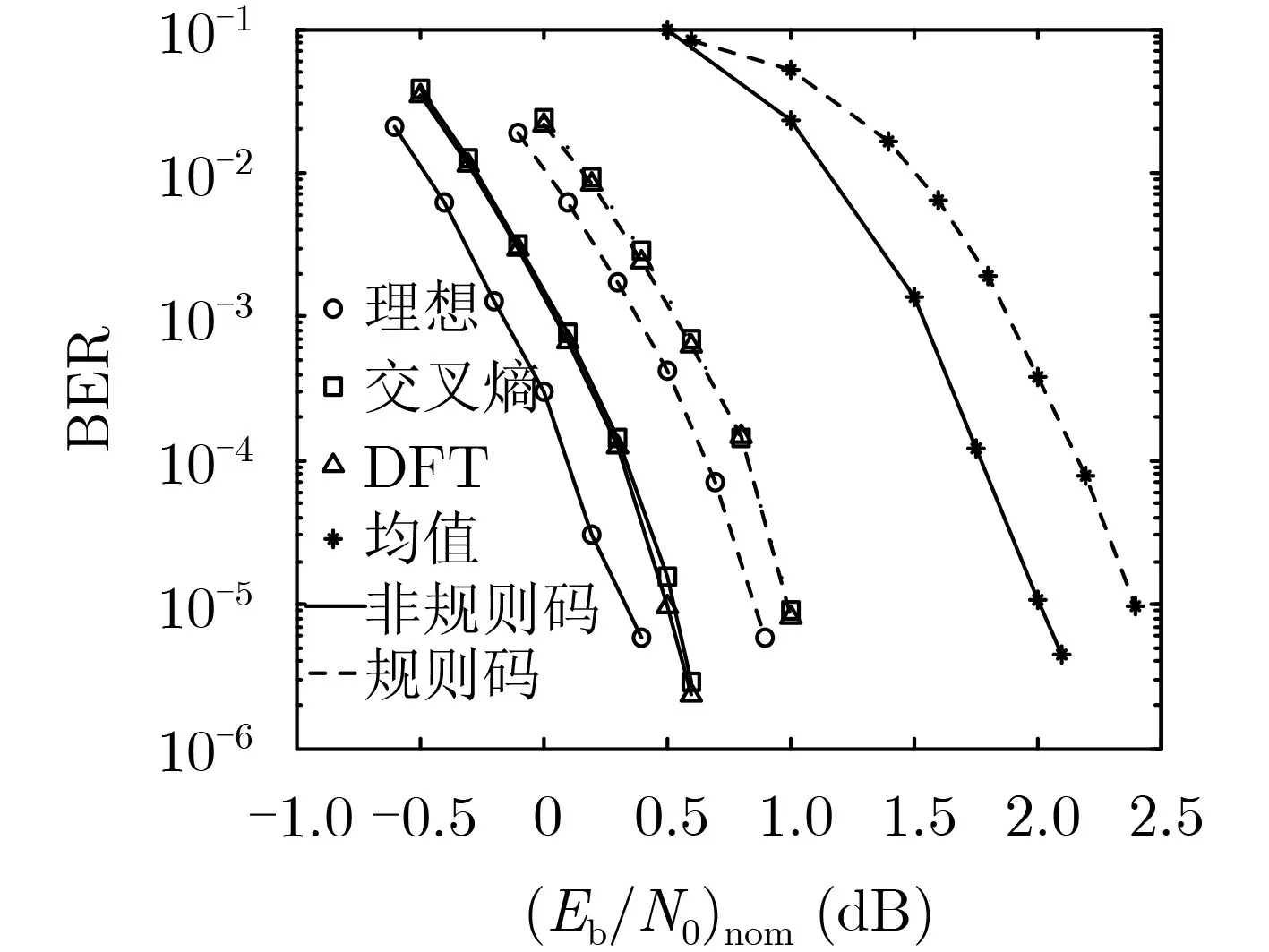
圖8 相同碼長的規則與非規則碼在所提JCED算法下的BER性能
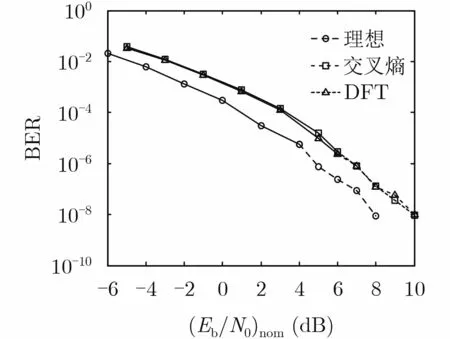
圖9 所提JCED算法的錯誤平層驗證
4 結束語
為解決非平穩信道下的高效信道估計與譯碼問題,提出一種基于SWBP的JCED算法。同時分別基于交叉熵和DFT提出兩種低復雜度的自適應滑窗長度設置方法。計算復雜度分析和仿真結果表明,基于兩種滑窗設置方法的JCED算法有著幾乎相同的接近最優的BER性能,在BER= 10?5時與理想信道估計下的BP譯碼算法僅有0.25 dB以內的性能差距,但基于DFT滑窗設置方法的JCED算法有最低的計算復雜度,其單輪迭代計算復雜度僅比BP譯碼算法高22%。同時,所提JCED算法對局部噪聲方差初始估計值不敏感,即使信噪比失配達±6 dB也不會影響BER性能,算法有很強的魯棒性。對不同碼長,不同碼率,規則與非規則碼的大量仿真結果表明,在非平穩信道條件下,所提JCED算法對所考察的碼的BER性能提升均有效,特別是對中低碼率的碼。另外,通過仿真驗證了所提JCED算法在BER=1 0?8時不會導致錯誤平層。

