密立根油滴實驗再認識

董 鍵

(曲阜師范大學物理工程學院，山東 曲阜 273165)

密立根油滴實驗已經做過100多年了[1-3]，由于其獨特的科學價值和教學價值，一直以來被各個大學選為學生實驗，一代一代的大學生都在重復做著該實驗，學生們喜歡做這個實驗，因為它能直觀地證明電荷的不連續性，即電荷量是量子化的，這個科學事實太重要了.然而，對這樣一個經典實驗，當下存在著不同做法，有的做法不甚合理，甚至不甚科學，沒有發揮好該實驗的科學認知和實驗訓練的價值.眾所周知，油滴實驗的科學內容分為兩個方面，定性的方面是電荷量量子化，定量的方面是測量基本電荷.作為定性特征，要證明電荷是不連續的，自然不能拿一個電荷量的值做為證據，但也不能只靠少數幾個油滴的電荷量就做出結論，它需要足夠多的油滴數據，用統計分析進行證明，重要的是讓數據說話，而不能“替數據說話”，即不能事先假定電荷量是量子化的，用“倒過來”的方法來證明量子化.這個道理，很多人都是認同的，但具體到對學生的要求上，就是另一回事了，原因是學生實驗時間有限，測不了很多油滴，于是，有的作者開始“替學生著想”，用各種“后期算法”來“證明”，幾個油滴的數據(10個以內)也能證明電荷量量子化，仿佛有“捷徑”可走.另有一些作者，將不同年級學生實驗的數據收集起來，數量上千個，著實足夠，但卻忘了來自不同儀器和不同學生的數據精度參差不齊，不能混用.更有的作者，自己不做實驗，從網上搜集他人數據，用繁瑣的算法，計算基本電荷的值，這樣做的意義值得懷疑.在各種油滴實驗的做法中，往往對于考察電荷量定性性質方面不突出，而把精力集中在計算基本電荷的數值上，對于后者，又不是著重把數據測得更準，而是試圖用算法將基本電荷“算的更準”[4-8].如果不加以澄清，將會降低油滴實驗的科學意義，弱化該實驗在學生心目中的形象，使學生漫不經心地對待該實驗，以湊合著交差過關為目標，那就可悲了.

基于以上認識，本文用“平衡法”重做油滴實驗，希望提供不同的參考視角.文中嚴格求解實驗方程組，認真對待布朗運動，把平衡態掌握得更準，分析對下落時間求平均的必要性，使電荷量測量誤差顯著減小；采用新的電荷量作圖法，簡潔地顯示電荷量的分組性即量子化，由此衍生出元電荷新的計算方法；導出電荷量測量誤差的分布規律，并用測量數據的有效數字的限制進行了解釋，為選取合適的油滴奠定了理論基礎.實驗采用南京培中科技開發所MOD5型油滴儀.

1 油滴實驗的“平衡法”

密立根油滴實驗的“平衡法”主要分兩步，第一步是將帶電油滴控制在均勻電場中靜止，電場由兩個平行電極板提供，見圖1.第二步是將板極電壓調整到零，讓油滴自然下落，進入勻速運動狀態.先不計空氣浮力，這兩步對應的方程組是

(1)

mg=6πηrv

(2)

其中m是油滴的質量，g是重力加速度，d是極板間距，U是板極電壓，r是油滴半徑，η是空氣黏滯系數，q是油滴所帶的電荷量(實驗測量的目標)，v是油滴勻速下落的速度，它可以通過測量油滴經過豎直高度l所用的時間t來計算.

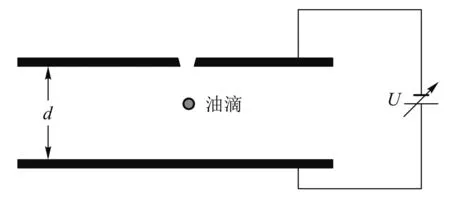
圖1 油滴實驗原理圖

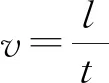
(3)

方程(1)和(2)有3個未知量：r、m和q，不能求解，需要補充一個關系式：

(4)

其中ρ是油的密度.考慮到油滴的尺度是微米量級，空氣的黏度需要用下式修正，

(5)

η0是用宏觀方法測量的黏度，它是溫度的函數，需要事先測量出來；p是實驗時的氣壓，氣壓和溫度都需要測量；b是修正常數，取為8.23×10-3m·Pa.

現在可以求解方程組(1)、(2)和(4)了，得到油滴半徑和電荷量，教科書上給出的都是近似公式，現在，計算軟件很發達，例如Mathematica，嚴格求解，結果如式(6)、式(7)所示.

(6)

27bglp2ρ0η0t-2b3g2ρ2t2]

(7)

實驗是在寒假里進行的，實驗室停暖，室內氣溫0 ℃(有助于降低油的揮發)，氣壓1.01×105Pa，采用701鐘表油，密度991 kg/m3，黏度1.91×10-5kg/m/s，當地的重力加速度是9.797 m/s2，l=2.00 mm，d=5.00 mm.

2 布朗運動的影響

“平衡法”的兩步都明顯受到油滴布朗運動的影響，是實驗中最大的影響因素，需要認真對待.首先，由于布朗運動，油滴無法靜止，給判斷何時才是重力與電場力的平衡狀態帶來了莫大的難度.模擬計算顯示，即使重力與電場力平衡了，布朗運動也會導致油滴持續向一個方向運動[9]，比如往上運動，沒有經驗者就會認為板極電壓大了，減小之，如此反復，最后沒有了衡量標準，隨便取一個“差不多”的電壓作為平衡電壓.正確的判斷方法是：將油滴移動到屏幕某條水平格線附近，如果能保持幾秒不離開格線，以后即使離開了格線，向一個方向運動，不要馬上調整電壓，觀察其運動，若油滴還能反方向運動，說明板極電壓離平衡電壓不遠了，再將油滴移動到格線上，觀察還能否保持不動，微調板極電壓，使之保持幾秒不離開，這個電壓就可以作為平衡電壓.這個過程可能反復幾次，需要若干分鐘，沒有耐心不行.若只看油滴短時間不離開格線就決定其平衡態，有時候會導致10～20 V的誤差.

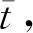
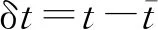
(8)

豎直線段表示某個油滴下落時間的殘差分布范圍.

圖2 油滴下落時間的殘差分布

表1是從所測油滴選出來的代表，它們的下落時間分布更具體的展示出來，隨著下落時間的增長，時間的起伏增大，好像比線性增大的更快，最短時間與最長時間差別可達8 s，這遠遠超出了人按按鈕的反應時間0.2s，這種起伏就是布朗運動影響的證明.經驗表明：對于一個計時熟練的人來講，下落時間小于15s，測量一次就夠了；時間大于15s之后，就需要反復測量，用平均值作為計算用的下落時間，因為起伏相對于平均值是對稱分布的.這是一個利用誤差分布特點來減小誤差的很好的例子，取平均方法的合理性也被關舒月等人的模擬計算所證明[10-11].

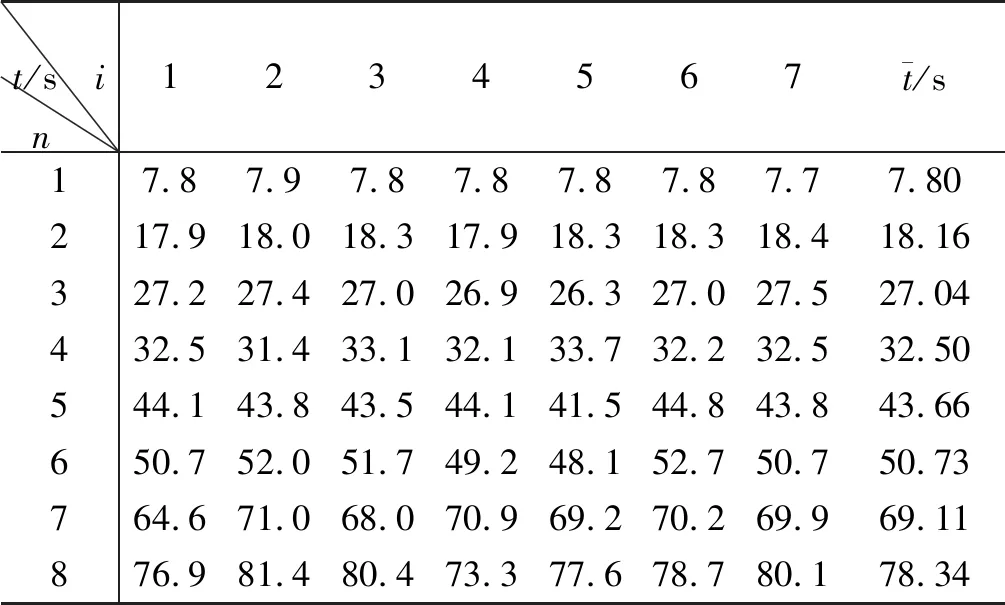
表1 反復測量的油滴下落時間分布 (n：油滴編號，i：測量次數)

3 “電荷量-編號作圖法”證明電荷量子化

油滴實驗的作用就是證明電荷的量子化，這不能通過一個油滴的電荷量來證明，必須通過大量油滴的測量，用統計比較的方法來證明，如果電荷量有分組性，就證明是量子化的.為此，筆者要求學生至少測量20個油滴，才能用電腦進行計算，用下面的作圖方法來顯示電荷的量子性：用油滴的編號n做橫軸，用電荷量q做縱軸，簡簡單單地將電荷量“曬”在平面上.表2是筆者測量的120個油滴的平衡電壓和下落時間數據，圖3展示了根據這些數據計算出的油滴電荷量分布，具有明顯的分組性，即：同一組的電荷量近似相等，不同組之間是寬大的無電荷區，電荷量子化的特性得到直觀的統計證明，這樣給學生的印象更深刻.

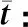
表2 平衡法測量120個油滴的實驗數據(U：平衡電壓，下落時間平均值)

4 求基本電荷

圖3 油滴電荷量子化的圖示

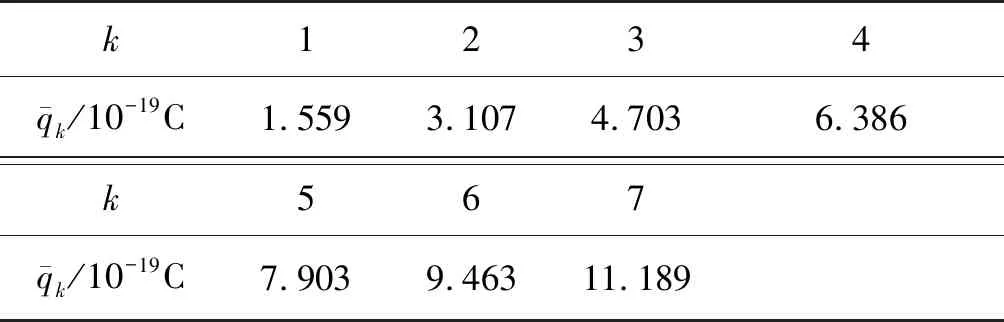
表3 各組電荷量的平均值(k：組別)

作電荷量平均值隨組別k變化的圖，見圖4.該圖顯示，不同組的電荷量呈良好的線性增大，若做線性擬合，數據點都靠近擬合線，這就是前述電荷量分布特點的定量表示，其中擬合線的斜率自然就是基本電荷e了，其值為(1.585±0.005)×10-19C,這就是圖3縱軸分度值的由來.順便指出，若計及空氣浮力項(0 ℃，空氣密度1.293 kg/m3)，則用同樣的測量數據計算的基本電荷是1.587×10-19C，僅對e值小數點后第三位帶來小的修正.如果擬合時取的電荷組數再小一些，e的值會有所不同.

圖4 各組電量平均值的分布與擬合線

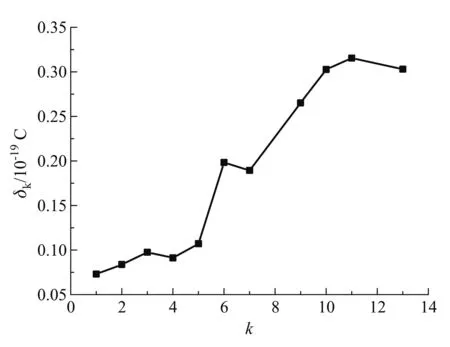
圖5 各組電量標準差的分布

5 電量測量誤差的分布規律

在計算每組電荷量平均值的時候，同時也算出了該組電荷量的標準差δk，其分布曲線見圖5，k是組序號(圖中缺少第8和第12組的數據，因為從圖3畫三角形的兩個地方看，那些組只有一個數據，不能計算標準差).曲線顯示，標準差的分布趨勢是隨著組別k的增大而增大的，由此推論：當電荷量誤差超過半個基本電荷時，就無法判斷該電荷量屬于哪個分組，量子化就無法證明了.圖3中用紅線圈起來的兩個數據點就屬于這種情況.因此，相對誤差的概念在本實驗是失效的，降低絕對誤差是本實驗所要求的.

圖5顯示的規律是客觀的，為什么會這樣呢？筆者發現，這個規律的來源有一個簡單的解釋，它來自測量儀表有效數字的限制[12]，具體來說，油滴儀電壓表和計時器都是三位的，所顯示數據的最后一位是不準確的，導致電荷量計算值有效數字也是三位(計算中間值多保留一位)，最后一位也是不準確的.

設電荷量計算值的三位分別用a、b和c表示，a不能為0，計算結果有3種可能，即a.bc、ab.c和abc(略去10-19C，余同).由于c是不準確的，它的波動范圍是0～9，該范圍對于不同的電荷量含義不同，對于a.bc，意味著電荷量的最大波動為0.1；對于ab.c，意味著1；對于abc，意味著10.因此，電荷量誤差隨著電量的增大一定是增大的.由此推論：因為當電荷量波動超過半個基本電荷(0.8)時，就無法證明量子化了，換言之，從ab.c開始，誤差就可能導致量子化證明的失效，必須選擇電量小的油滴，例如電荷量不超過10.0×10-19C，也就是在7個最低的分組之內.雖然有的作者是這么做的[13]，但是依據不充分、不定量，以上分析，給選擇油滴提供了定量依據.

6 選擇油滴一定要很苛刻嗎？

上面是從電荷量大小的角度對選擇油滴做出了限定，由于電荷量是由平衡電壓和下落時間來計算的，自然就提出了對平衡電壓和下落時間限定的問題.由于電荷量是雙變量函數，選擇的范圍就多樣化了.不少作者根據自己的分析和喜好，各自做出了選擇，例如：高鐵軍主編的《近代物理實驗》就約定電壓取200 V附近的值，時間15 s～30 s[14]；于津江等限定時間20s～30 s，電壓200 V附近，帶電荷2～4個[15]；劉芬等主張時間20s～30 s，電壓100 V～250 V，帶電荷不大于5個[16]，等等.時間范圍和電壓范圍普遍較窄，筆者認為這過于苛刻.事實上，凡是滿足電荷量計算公式的電壓和時間，都是可取的，只要能控制測量誤差到可以接受的程度，例如如上面測量的120多個油滴所做的那樣.在這些油滴中，電壓取值62 V～634 V，時間取值5.5 s～78.3 s.為了顯示在“極端條件”下所測量的油滴電荷量是否有很大的誤差，筆者從以上油滴中選擇了10個，其參數和電荷量見表4，電荷量的分布見圖6，可見，電荷量的誤差并不大，與所在組的電荷量均值靠的很近.既然如此，對油滴的選擇條件就可以放寬：時間10s～60 s，電壓大于100 V.這樣，學生選擇起來就容易多了，能把精力更多地放在誤差控制上，也有利于測量更多油滴.

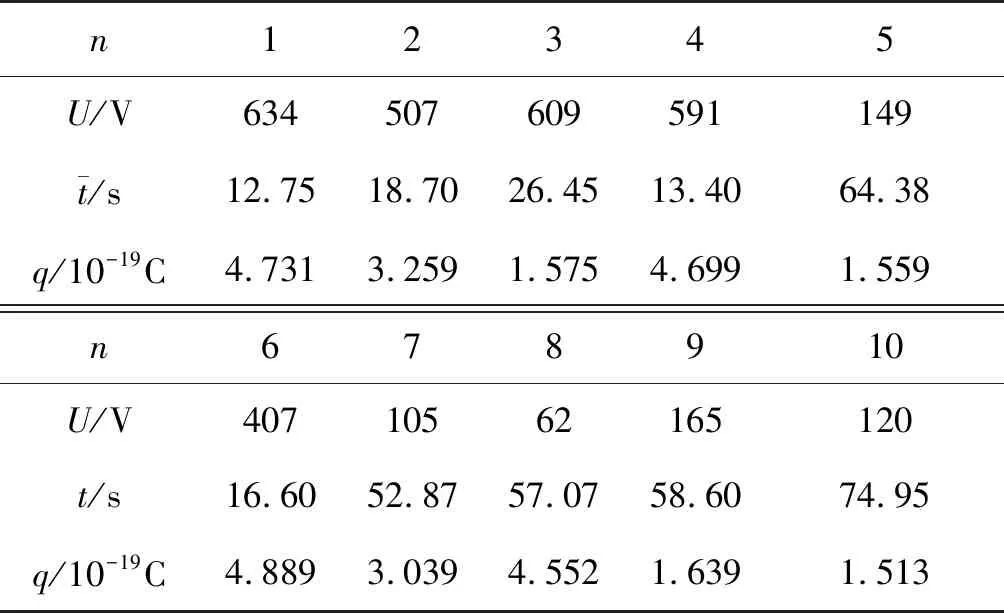
表4 部分“極端”油滴的電荷量(n：油滴編號)

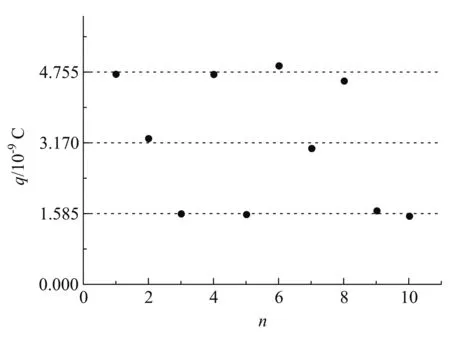
圖6 部分“極端”油滴的電荷量分布

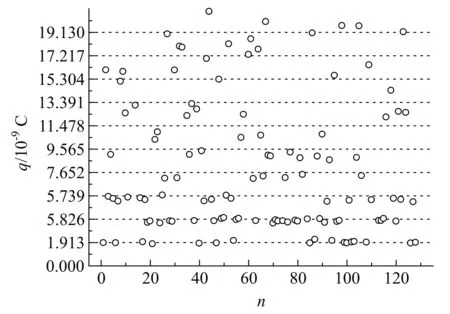
圖7 不計空氣黏度修正的電荷量分布

7 若不計黏度修正會怎樣？

式(5)是黏度的修正公式，是密立根創造的一個重要理論成果[17]，它是在實驗上發現當油滴較小時，電荷量計算值偏大，而想到了微米尺度上空氣的不連續性對油滴下落的影響，依據氣體運動論推導出來的一個近似公式，后來證明這個修正是十分必要的，修正之后，電荷量的計算值才趨于量子化.在今天的實驗教學中，學生很少去想這個修正項的來源和必要性，普遍缺乏對修正項作用的認知.其實，只要對測量數據按照非修正公式(即在式(7)中令b=0)再算一遍，結果就由圖3變為圖7，數據點改用圓圈標記.該圖顯示，電荷量的起伏性隨油滴電荷量的增大而迅速增大，在第四組之后，就難以辨認分組性了，數據點幾乎均勻分布在平面上，好像撒了一把沙子.在下部4個可辨認的分組中，若取每組的平均值當做該組的電荷量，則相鄰兩組電荷量的間隔也不再相等，且都大于1.77，第一組的電荷量最大，達到1.913，遠遠大于元電荷的值，即使拿第一組的平均值當做元電荷也不行.

8 述評

在密立根油滴實驗中，只要測量的油滴數量足夠多，只要將油滴的電荷量按編號作圖，電荷量量子化就能直觀地顯現，無需設計其他算法去證明，電荷量量子化是統計結論.根據經驗，適當限制平衡電壓和下落時間的范圍，可以將油滴的電荷量控制在10個基本電荷以內，誤差也會減小，更有利于量子化的結論.

油滴實驗的主要誤差來源是油滴的布朗運動，可以針對性地采取措施，減弱誤差的影響，但效果有限，由于還涉及更多的因素，用油滴實驗測量基本電荷，精度不易提高.當人們接受了電荷量子化的理念之后，還可以尋求其他途徑測量電子電荷，例如塞曼效應，半導體PN結的伏安曲線等等，以開闊學生的視野.

油滴實驗給了學生思考很多物理問題的機會，例如：油滴是如何帶上電荷的？這將給物質帶電機制以怎樣的啟發？如何更好地描述油滴的運動？油滴揮發速率多大，將給實驗帶來多大的影響？油滴實驗原理還有其他用途嗎？等等.

油滴實驗還給學生提供了數據分析的很好范例，借助于適當的計算軟件，克服“數據分析恐懼癥”，不再面對著一堆雜亂的數字發呆，只要有想法，軟件就可以助力“拷問”數據，讓它回答不同的問題，以充分發掘數據的潛力.這樣內含豐富的經典實驗，值得師生認真對待，倍加珍視，使之成為學生心目中的科學里程碑.