爆炸/沖擊動力學學習研究中的若干疑惑*

王禮立

（寧波大學沖擊與安全工程教育部重點實驗室，浙江 寧波 315211）

自1981 年創刊，《爆炸與沖擊》走過了不平凡的40 年。40 年，就人生而言誠可謂不惑之年，而就期刊而言則尚可謂青春靚麗、朝氣蓬勃。《爆炸與沖擊》作為我國力學園地的一枝新秀，即使以異軍突起相夸，也不為過。

爆炸與沖擊學科所面臨的是一系列新興的跨學科或邊緣學科研究，這迫使我們必須如饑似渴地加倍學習，怠惰就會落后，落后就會屈辱地挨打。爆炸與沖擊學科面臨的大量研究沒有現成的答案，惟有靠我們去突破創新，只模仿不創新就會落后，落后就會屈辱地挨打。唯有在學習和創新的緊密結合中，才能出新成果，出高水平人才。

從20 世紀60 年代開始，我有幸加入爆炸與沖擊學科的研究和教學行列，80 年代隨《爆炸與沖擊》一起成長。如今已年屆耄耋，回顧往事，感到從學習走向創新的過程中，疑惑是創新的前奏，是我要感謝的啟蒙老師。

在學習研究爆炸與沖擊學科的過程中，我遇到過很多疑惑，略舉數例：在分析爆炸與沖擊相關的動力學問題時可以同時采用靜力學平衡條件嗎？滿足屈服條件（σeff=Y）就一定進入塑性了嗎？ZWT 方程的黏彈性松弛時間θ1和θ2為什么互相無關？有質量就有慣性嗎？絕熱剪切失效要不要考慮慣性效應？層裂是材料動態響應問題還是結構動態響應？基于塑性鉸的結構塑性動力學分析與波傳播分析有什么相通的內在聯系？

值此慶賀《爆炸與沖擊》創刊40 周年之際，和大家分享我在這方面的感受。

1 在分析動力學問題時可以同時采用靜力學平衡條件嗎？

弦在斜向沖擊下的彈塑性波傳播是一個彈塑性縱波與橫波相耦合的復雜問題，Paxмaтyлин等[1-2]最早對這個問題作了奠基性的研究。如圖1 所示，橫波波陣面以折斷點的形式傳播，表現為質點速度矢量v的強間斷；彈塑性縱波則在折斷點兩側的弦中傳播，等同于桿中一維彈塑性縱波的傳播。于是，弦中張力/應變擾動由縱波傳播，而橫波只引起弦的形狀改變，但兩者通過波速關系相耦合。縱波波速為：

式中：ρ0為弦的初始密度，T0、ε0為初始張力、應變，其他符號如圖1 所示。

對于直弦受突加恒值斜向點沖擊的情況（見圖2），問題的復雜性在于需要區別兩種不同的沖擊類型[1-3]：（1）沖擊物與弦之間沒有相對滑動，稱為無滑動沖擊，沖擊點是駐定的強間斷面；（2）沖擊物與弦之間發生相對滑動，稱為滑動沖擊，沖擊點是運動的強間斷面。

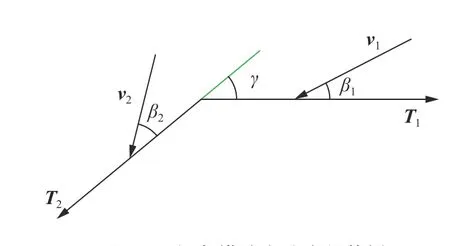
圖 1 強間斷橫波在弦中的傳播Fig. 1 A strong discontinuous transverse wave propagating in a string

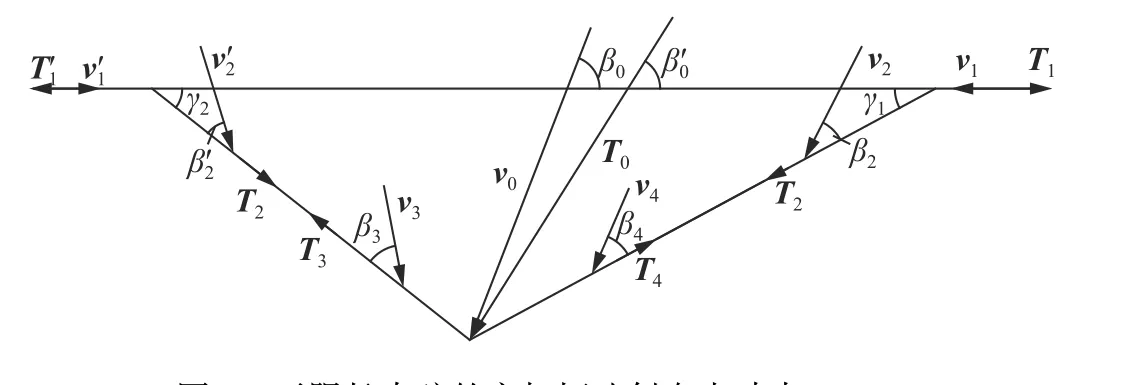
圖 2 無限長直弦的突加恒速斜向點沖擊Fig. 2 An infinite straight string subjected to abrupt constant-velocity oblique point-impact

這時，根據跨過各個間斷面（包括沖擊點間斷面）上的動力學條件、運動學條件和本構關系，共可以列出20 個方程，其中包含21 個未知量，還需要加1 個沖擊點處的物理方程，從而可以組成21 個方程，解出21 個未知量。對于無滑動沖擊，相當于求解半無限長的直弦受突加恒值斜向沖擊的問題，由于沖擊點處的邊界條件是確定的，因而是定解的。但對于滑動沖擊，所處理的是一個變邊界問題，外載荷作用的邊界本身是待定的，需要補充1 個表征滑動沖擊特征的物理方程。

Paxмaтyлин[1]最早研究了這個問題，采用了機械工程中繩索繞滑輪的Euler 公式：補充這個方程后，問題就可正確求解了。值得特別懷念的是，文獻[5]由當時的《力學學報》主編郭永懷先生審定刊發，成為我第一篇發表的有關塑性波的研究論文。

類似的、不無惋惜的是，Tan 等運用激波理論來分析泡沫材料動態力學行為的論文[6]本是一篇好文章，疑惑卻出現了：在文中采用了準靜態孤立系統中的能量守恒條件，從而導出的激波形成的臨界速度公式是錯誤的。我們利用跨過激波的能量守恒條件即Rankine-Hugoniot 關系，建立了正確的第一臨界速度和第二臨界速度[7-8]。這類把習慣的準靜態分析與動態的波傳播分析相混淆而導致錯誤的教訓，實在值得引以為戒。

2 滿足屈服條件（σeff=Y）就一定進入塑性了嗎？

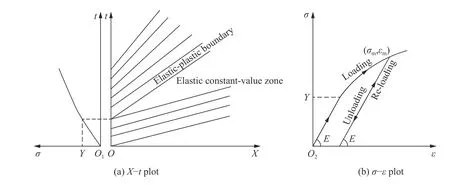
圖 3 桿中一維彈塑性加載波的傳播Fig. 3 One-dimensional elastic-plastic wave propagating in a bar

這意味著式（4）只適用于經典塑性靜力學，而不適用于以應力波傳播為特征的塑性動力學。問題出在哪兒呢？在塑性靜力學分析中，人們關注的主要是應力應變曲線本身，而在塑性波分析中，應力應變曲線的斜率具有更重要的意義，是它決定了波速（見式(5)）。由圖3(b)可見，屈服點（或后繼屈服點）恰好是曲線斜率的奇點（斜率的間斷點），應力波波速在該點具有多值性。因此，式（4）在塑性動力學中只是必要條件，而不是充要條件。

從屈服點處斜率奇性（波速奇性）出發，動態屈服條件的雙變量準則應為[9-11]：

對于后繼屈服點σm（見圖3(b)），只需以σm代替上式中的Y即可。

正是從彈塑性加卸載時波速奇性這個基本奇性出發，我們進一步發展了彈塑性邊界傳播速度基本規律的系統性研究[9,12-14]。國際非線性應力波理論權威、《Applied Mechanics Reviews》副主編Ting（丁啟財）[15]曾專門撰文詳細介紹這個成果，指出：“這是一個出眾的結果”。

3 ZWT 方程的黏彈性松弛時間θ1 和θ2 為什么互相無關？

工程適用的非線性黏彈性本構關系，一直是非線性黏彈性波理論發展的瓶頸。唐志平等[16]、王禮立等[17-18]在理論上從Green-Revlin 多重積分方程出發，在實驗上通過對各種典型工程塑料（如環氧樹脂、有機玻璃PMMA、聚碳酸酯PC、尼龍PA、ABS、PBT、PP/PA 共混塑料等）的實驗研究，發現在準靜載荷到沖擊載荷的廣闊應變率范圍，即在應變率范圍為10-4～103s-1時，高聚物的非線性黏彈性本構行為可以令人滿意地由如下非線性黏彈性本構關系（朱-王-唐方程，ZWT 方程）描述：

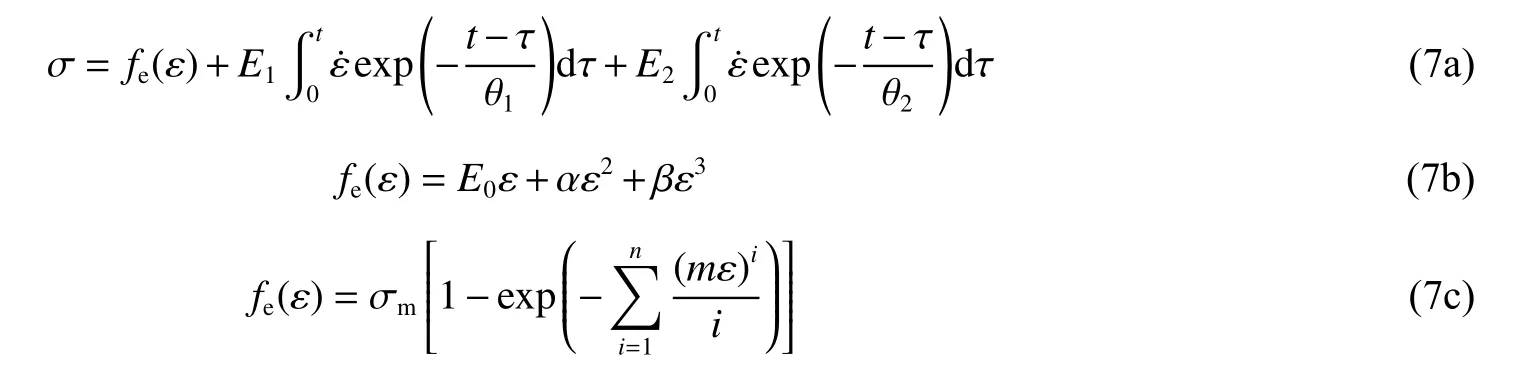
式中：fe(ε)為非線性彈性平衡響應的描述，用式（7b）描述時E0、α 和β 為對應的彈性常數[16]，用式（7c）描述時σm為 ε →∞ 時fe(ε)的漸近最大值，m為E0和σm的比，而正整數n為表征fe(ε)初始線性度的材料參數[19]；第1 個積分項描述低應變率下的黏彈性響應，E1和θ1分別為所對應的Maxwell 單元Ⅰ的彈性常數和松弛時間；第2 個積分項描述高應變率下的黏彈性響應，E2和θ2則分別為所對應的Maxwell 單元Ⅱ的彈性常數和松弛時間。實驗表明，θ1通常為10～102s 量級，而θ2通常為10-4～10-6s 量級，兩者相差約6 個量級。他們分別對低應變率響應和高應變率響應負責，互不相關。ZWT 方程雖然是我們提出的，但在心中同樣有過一個疑惑，為什么θ1和θ2互相無關？這個疑惑激勵我們作更深入的探索。

進一步的研究表明[20]，每個Maxwell 單元的松弛時間θi存在一個有效影響應變率范圍（見圖4），約占4.5 個量級，稱為有效影響域（effect influence domain, EID）。所以不難理解，θ1對低應變率響應負責，而θ2對高應變率響應負責。并且，θ1和θ2將各自在自己的有效影響域范圍發揮作用，兩者相差大約6 個量級，互相獨立無關。這樣，在1～102s 時間尺度的準靜加載條件下，具有松弛時間θ2為1～102μ s 的高頻Maxwell單元從準靜加載開始就已經完全松弛了。反之，在1～102μ s 時間尺度的沖擊加載條件下，具有松弛時間θ1為10～102s 的低頻Maxwell 單元將無足夠的時間來松弛（直到加載結束）；這時，低頻Maxwell 單元化為彈性常數為E1的簡單彈簧。

以前，我在英國劍橋大學Cavendish 實驗室從事研究期間，有一位多年從事高聚物動態力學響應的研究人員和我討論，為什么不能用常規的振動法獲得高聚物高應變率下的材料本構關系？我就用圖4的有效影響域說明，這就像中國的歇后語—鐵路警察各管一段，獲得了他的贊賞。

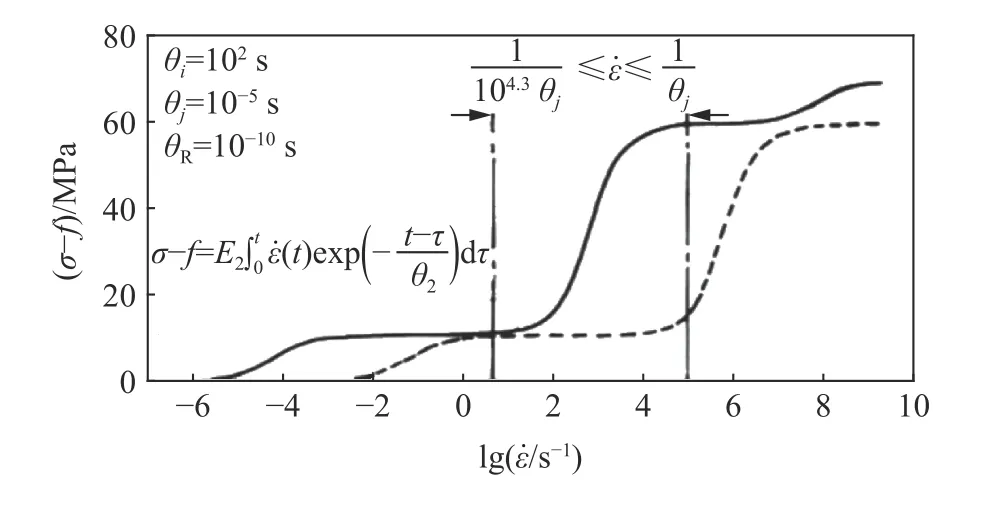
圖 4 松弛時間的有效影響閾Fig. 4 The effect influence domain of a relaxation time

進一步的研究還表明，既然任任意θi存在一個有效影響域，約4.5 個量級的應變率（或時間）范圍，因此就黏彈性波的傳播而言，也存在一個由高應變率松弛時間θ2占統治地位的有效傳播時間teff=θ2或有效傳播距離Xeff=cvθ2[21]。超出此有效傳播時間或有效傳播距離占統治地位的區域，θ2不再發揮顯著的影響作用。不論對研究黏彈性波的傳播特性（正問題），還是由黏彈性波傳播的實測波形反推材料本構關系（反問題），這都有直接的指導意義。

4 有質量就有慣性對嗎？絕熱剪切失效要不要考慮慣性效應？

曾經與一位國際知名學者討論，高應變率下材料的絕熱剪切（熱黏塑性失穩）要不要考慮慣性效應，我認為對于材料動態響應需要考慮的是應變率效應而不是慣性效應，他則認為應該考慮慣性效應，原則性理由是有質量就有慣性。當時的學術討論雖然沒有取得共識，但有益的交流給我留下了一個疑惑，有質量就有慣性普遍成立嗎？

不妨設想一個簡單的情況，在爆炸/沖擊載荷下，Hooke 定理需要增加慣性項嗎？答案顯然是否定的。那么關于有質量就有慣性問題的爭議點出在哪兒呢？其實問題出在從概念上混淆了結構響應與材料響應[22-23]。的確，早期的力學研究者限于當時的歷史條件，常常對結構響應與材料響應不加區分，無形中一直會影響后來者。例如，有關材料力學的教材可以追溯到20 世紀30 年代Timoshenko 的著名經典著作《Strength of materials》[24]。而實際上，只有小部分內容涉及材料的力學性質和強度（材料響應），大部分內容主要講授代表性結構元件（桿、軸、梁等）受力時的應力-應變分析（結構響應）。結構響應與材料響應的關系可以通過強度準則關系式來討論。強度準則一般可概括為：

式(8)將力學特征量Σ 和材料特征量Σc相聯系：Σ 屬于結構響應，要依靠力學家對結構力學場進行分析得到（但在力學分析中要依賴材料本構關系）；Σc屬于材料響應，要依靠材料學家對材料進行實驗研究確定（但在材料試驗中要依賴力學分析）。強度準則建立了結構響應和材料響應之間的聯系，兩者既有區別又相耦合。

由此可見，就結構響應而言，通過動量守恒方程，有質量就有慣性是成立的；但就材料響應而言，不涉及動量守恒方程，有質量就有慣性就不成立，需要考慮的是應變率效應。文獻[4]和文獻[25-26]正是就這兩方面分別展開討論，并在后者中，格外強調了結構響應與材料響應的區別和聯系。

還應該指出，對于絕熱剪切問題，可以分別從結構響應角度和從材料響應角度進行研究。從宏觀的連續力學出發，在結構響應研究中，結構物中凡滿足絕熱剪切準則的區域形成宏觀的絕熱剪切區（不是顯微觀察到的絕熱剪切帶！），就像結構物中凡滿足屈服準則的區域是宏觀的塑性區（不是顯微觀察到的塑性滑移帶！），爆炸/沖擊載荷下的這類研究當然計及慣性效應（應力波效應）。至于在宏觀力學的材料響應研究中，主要研究絕熱剪切的宏觀失穩準則，這類研究則不需要計及慣性效應，而應該計及應變率效應。

5 層裂是材料動態響應問題還是結構動態響應問題？

層裂（spalling 或scabbing）是爆炸與沖擊載荷下特有的動態破壞現象。層裂研究中的一個核心問題是：在滿足什么樣的定量臨界條件下發生層裂，即層裂準則（spalling criterion）的研究。Rinehart 最早提出最大拉應力瞬時層裂準則[27]：

式中：σc為表征材料抗動態斷裂性能的材料常數，稱為動態斷裂強度。這個準則在形式上是靜強度理論中的最大正應力準則在動態情況下的推廣。按照這個思路，層裂是材料動態響應問題。疑惑在于，層裂的發生離不開卸載波的相互作用，而應力波的相互作用則是結構動態響應問題。層裂到底是材料動態響應問題還是結構動態響應問題呢？

我們來看一下研究層裂破壞的一維應變平板撞擊實驗（見圖5）[25-26]。當飛片在氣炮驅動下以高速撞擊靜止的靶板時（見圖5(a)），在界面產生兩個壓縮波系，分別左行和右行傳入飛片和靶板，其波傳播時程圖如圖5(b)所示（這里已忽略強度較低的以虛線表示的彈性前驅波）。一旦兩個壓縮激波分別達到飛片和靶板的自由表面，就會卸載反射成以扇面形傳播的稀疏波系。當這兩波系在靶板（試樣）內部距離背面某個位置hs處迎面相遇，會產生一個高應變率、高幅值的拉伸應力區。一旦滿足某個材料動態拉伸破壞準則，該位置處材料發生層裂破壞。在實驗過程中，通常測量試樣背面的質點速度u隨時間t的變化，如圖5(c)所示。人們常利用u-t曲線上的回跳駝峰，來研究層裂是否發生、所包含的損傷演化信息及相應的層裂準則。

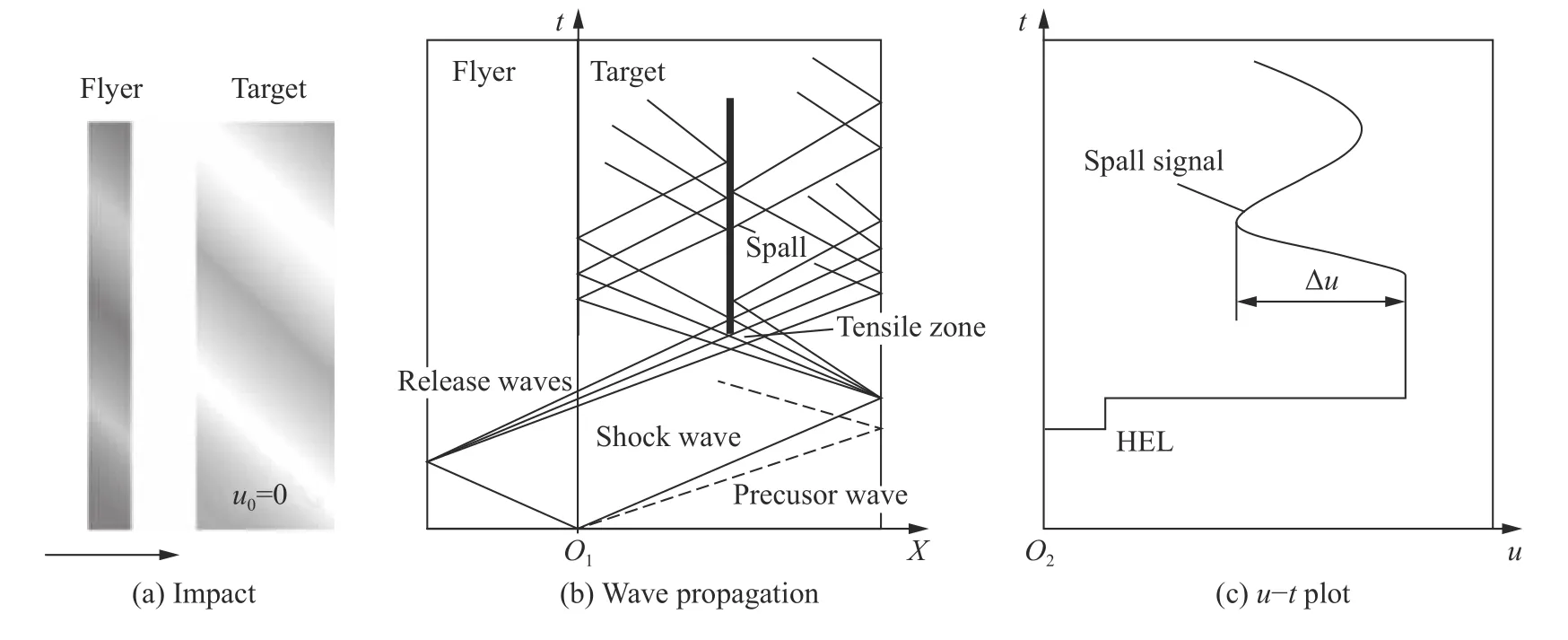
圖 5 層裂的平板撞擊實驗示意圖Fig. 5 Schematic of the plate impact experiment for spalling

由此可見，層裂既離不開卸載波的反射和相互作用過程（在這點上，表現為在結構物中發生的結構動態響應），又必須滿足某個材料破壞準則（在這點上，表現為在層裂質點處發生的材料動態響應）。因此，層裂既不是單純的材料動態響應，也不是單純的結構動態響應，而是兩者相耦合的響應。

其實，在材料動態破壞的其他研究中，如裂紋動力學和動態碎裂等，一旦破壞的發生發展涉及試件結構中的波傳播，或破壞以局域化的形式出現在試件結構中，都不再是單純的材料動態響應問題，而必須計及相耦合的結構動態響應，這使問題大大復雜化。

6 基于塑性鉸的結構塑性動力學分析與波傳播分析有什么相通的內在聯系？

梁中塑性彎曲波的分析一般涉及彎矩M-轉角速度ω 擾動傳播（M-ω 波）和剪力Q-橫向速度v擾動傳播（Q-v波）之間的互相耦合，這使問題變得十分復雜。作為一種有效的近似處理，Lee 等[28]在以下基本假設下發展了梁的剛塑性動態分析：(1)彈性應變εe與塑性應變εp相比可近似忽略（εp＞ ＞ εe），彈塑性梁簡化為剛塑性梁；(2)當|M|=M0（理想塑性彎矩）時，曲率κ 可無限增大，形成塑性鉸；(3)當|M|＜M0時，梁以剛體運動（忽略彈性彎曲波）。于是，問題歸結為研究以塑性鉸相聯的各梁段的剛體運動，這使問題的處理大大簡化。

疑惑在于：塑性鉸模型與彈塑性彎曲波理論在什么條件下一致？塑性鉸作為塑性變形集中的強間斷面，是否必須滿足應力波間斷面上的動力學條件和運動學條件？

以相對簡單的梁的橫向沖擊為例來討論，其動態失效一般有3 種基本模式：大撓度失效（Mode Ⅰ），拉伸撕裂失效（Mode Ⅱ）和橫向剪切失效（Mode Ⅲ）。對于橫向剪切失效（Mode Ⅲ），以前都采納Nonaka[29]的解。他基于理想剛塑性模型，引入了塑性剪切鉸。然而，剪切鉸作為強間斷面，跨過剪切鉸的橫向剪力間斷[Q]、橫向質點速度間斷[v]和剪應變間斷[γ]之間應滿足動力學條件和運動學條件[4]：

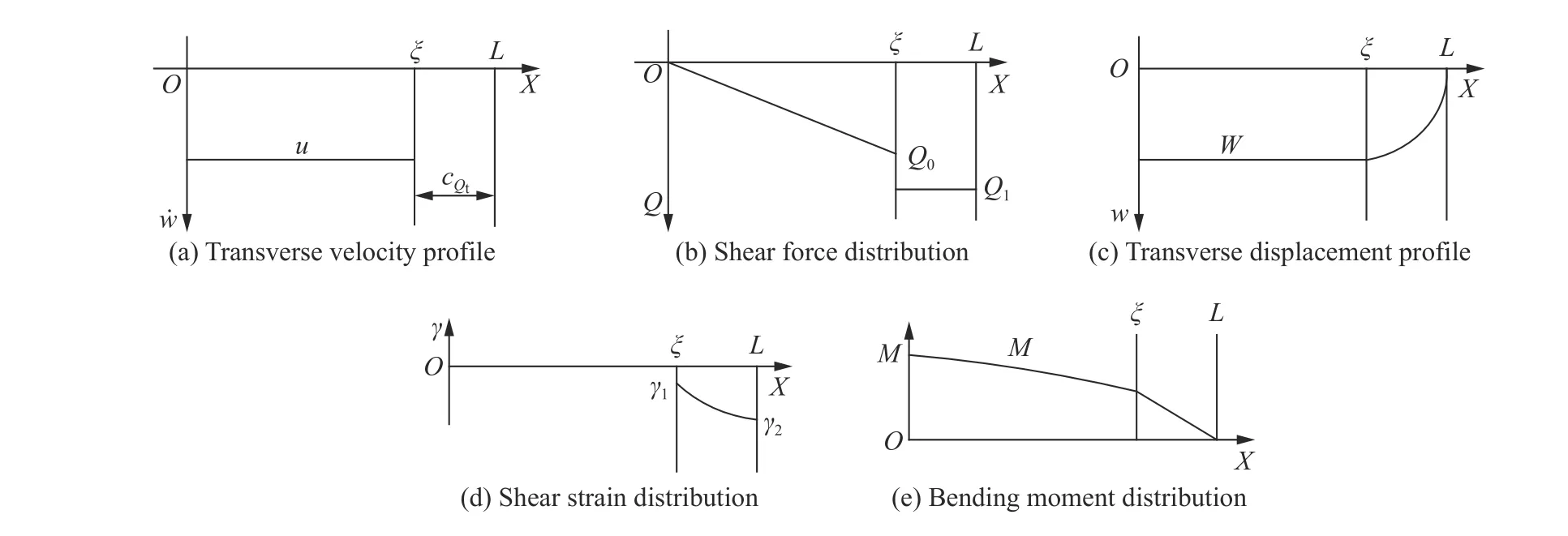
圖 6 簡支梁在沖擊加載下的橫向速度剖面、剪力分布、橫向位移剖面、剪切應變分布和、彎矩分布Fig. 6 Simply supported beam subjected to impulsive loading: transverse velocity profile, shear force distribution,transverse displacement profile, shear strain distribution, bending moment distribution

上述移行剪切鉸解，同時滿足強間斷上動力學條件和運動學條件。由此可見，理想塑性模型對波傳播是不適用的。同時還發現，Nonaka 解是移行剪切鉸解當移行剪切鉸傳播的距離Ls相對于梁半跨L小得可忽略時的近似解。Nonaka 肯定了我們的工作，并在分析1993 年紐約世貿中心爆炸案中的鋼支架破壞[31]時，直接引用了我們的論文。

上述移行剪切鉸解，給出了梁在橫向沖擊載荷作用下有以下3 種可能的剪切失效模式。（1）橫向大撓度模式：當橫向位移wf超過規定的臨界橫向位移wc（wf≥wc）時失效；（2）橫向剪切變形模式：當最大剪切應變γs超過規定臨界剪切應變γc（ γs≥γc）時失效；（3）絕熱剪切模式：當滿足絕熱剪切準則時失效[32-33]。其中，梁的絕熱剪切失效模式是一種新提出的失效模式。從此，其他人把這個失效模式稱為梁的第4 種失效模式（Mode Ⅳ）[34-35]。

7 結 語

根據以上討論，我的主要體會可以歸納為以下幾點。

（1）人們容易以靜力平衡的慣性思維來看問題，當以此來處理波傳播問題時，就會導致差錯，應引以為戒。

（2）人們容易把關注停留在應力應變曲線本身，但在處理波傳播問題時，還應更多關注會決定波速的應力應變曲線斜率，特別是斜率奇點如屈服點、卸載點和后繼屈服點等。這個奇性決定了彈塑性/加卸載邊界的傳播規律。也正由此，經典屈服條件式（4）只是動態屈服的必要條件，應代之以雙變量動態屈服條件式（6）。

（3）人們容易以連續松弛譜的觀點來研究黏彈性材料的動態本構特性，其實分立的每一個松弛時間θi都存在一個約占4.5 個量級的有效影響域和對應的有效傳播距離和有效傳播時間。正由此，包含兩個獨立無關松弛時間的ZWT 方程足以表征從準靜態到沖擊高應變率的材料動態響應，更適合工程應用。

（4）人們容易混淆結構響應和材料響應。對于爆炸/沖擊動力學問題，尤其應該強調兩者的區分和聯系。所謂有質量就有慣性，只在結構動態響應研究中成立；在材料動態響應研究中，此說不成立，而應該更多關注應變率響應。

（5）層裂這類動態失效，一方面離不開卸載波的反射和相互作用過程（結構動態響應），另一方面必須滿足某個材料破壞準則（材料動態響應）。因此，凡是涉及波傳播等結構動態響應的動態失效，都是兩者相耦合的復雜響應。

（6）通過對Nonaka 解的討論可見，塑性鉸分析中的塑性鉸實際上可看作波傳播分析中的間斷面。但在理想剛塑性假定下，塑性鉸傳播速度將化為零（對應于駐定塑性鉸），這類近似解會導致不能同時滿足間斷面上的動力學條件和運動學條件。引入塑性硬化假定，問題轉化為移動塑性鉸，將有利于同時滿足間斷面上的動力學條件和運動學條件，更加趨同于波傳播分析。

在學習研究爆炸/沖擊動力學過程中，我常常經歷了很多疑惑→解惑→再疑惑→再解惑······的過程。學問學問，包含著學和問，問就意味著發生疑惑。每個疑惑的解答就是一次提高，甚至是新一輪的創新工作。我深深感謝獨立思考中的疑惑對我的啟發和挑戰！希望在耄耋之年能繼續保持學生般的好奇和疑惑，啟發我們一起去深思求真、去迎接挑戰、去創新前進！