無監督域適應的表示學習算法

許亞雲，嚴 華

(四川大學 電子信息學院，成都 610065)

有監督的模式識別過于依賴有標簽的訓練樣本的數量.一方面，在現實生活中為樣本打標簽十分耗費資源和時間；另一方面，這種完全由樣本的數量和質量決定的學習方式非常容易導致過擬合.由于監督學習的局限性和不便利性，大量的研究者開始探索無監督和半監督的學習方法.如主動學習，它不是將所有樣本打上標簽，而是提出一些標注請求，將一些經過篩選的數據提交給相關領域專家進行標注.

域自適應或遷移學習，因為不需要大量的數據標注，近年來受到研究者的廣泛關注.在域自適應的問題中，將需要進行識別的數據集稱為測試集.測試集中的數據全部沒有標簽時稱為無監督域自適應[1-2]，測試集中有少部分數據有標簽時則稱為半監督域自適應[3-4].與主動學習不一樣的是，不需要采取人工輔助的方式為樣本打上標簽，用于訓練做訓練集的源域中已經擁有大量有標簽的數據，但是源域的數據和真正需要進行分類的目的域數據并不是同分布的.所以域自適應主要解決兩個域分布適應的問題，從而借助源域中大量有標簽的數據集對目的域的數據進行識別.目前傳統的域自適應算法的相關研究工作主要分為以下3種方式：1)數據分布的適應：即通過某種變換直接將兩個域的分布拉近或者選擇出分布相似的公共特征，主要通過最大平均差異(maximum mean discrepancy, MMD)[5]度量變換后的兩個域的相似性，例如TCA[6]、TJM[7]、JDA[8]和JGSA[9].TCA首先提出通過一個特征映射使得映射后的兩個域的邊緣分布接近，JDA同時考慮了邊緣分布適配和條件分布適配.其他部分方法基于TCA和JDA做出了擴展，例如TJM在TCA中加入了源域樣本選擇，ARTL[10]將JDA嵌入結構風險最小化框架.2)子空間學習：包括低維統計特征的子空間對齊(SA[11]、SDA[12]和RTML[13])和低維流形結構的子空間對齊(GFK[14]和DIP[15]).3)表示學習：在子空間學習的基礎上通過源域樣本表示目的域樣本(DTSL[16]和LSDT[17]).

1 域適應表示學習算法

本文的方法基于表示學習，與現有表示學習方法思想相同：都是在子空間學習的基礎上引入表示矩陣以更好地減少兩個域的分布差異.但是現有方法通常只采用一個單一的表示矩陣來建立兩個域之間的映射關系.本文的方法與之不同：1) 本文改進地采用兩個不同的表示矩陣，分別用源域表示目的域和用目的域表示源域；2)同時提出兩個表示矩陣各自的最優化約束設計，使得源域和目的域最優地相互表示，從而減少域差異，實現借助源域數據對目的域無標簽數據的分類.

1.1 源域有監督子空間學習

域自適應問題最關鍵的是減小兩個域的差異.通常可以通過尋求一個兩域的共同子空間去實現兩域之間的遷移.由于源域具有可靠的真實標簽，首先在源域學習一個標簽引導的子空間.模型如式(1)所示

s.t.C≥0，

(1)

式中：⊙是Hadamard乘積運算，P∈Rm×d是共同的子空間，Xs∈Rm×ns是源域的數據，Ys∈Rd×ns是源域標簽矩陣，m是樣本特征的維度，ns代表源域樣本的數目，d是共同子空間的維度.C∈Rd×ns是松弛標簽矩陣，加入松弛標簽C是為了更自由地獲得共同子空間.

1.2 構建表示矩陣

通常引入表示矩陣可以促進共同子空間的學習.常見的方法是使用一個表示矩陣，即單一方向地用源域的數據表示目的域數據，或者目的域數據表示源域數據，例如DTSL和LSDT.但這樣的表示方式下，兩個域的有用信息很難被完全保留.這是因為源域和目標域的特征分布不同，兩個域需要保留的信息不同，而使用同一個表示矩陣不能很好地保留兩個域特有的有用信息和結構特征.尤其是，當帶有標簽的源域樣本單方向地靠近目的域數據時，會對源域的基本結構造成一定的破壞.

于是本文提出在源域和目的域采用兩個不同的表示矩陣來表示另一個域.即在源域存在一個表示矩陣去表示目的域的特征，同時在目的域存在另一個表示矩陣去表示源域的特征.該模型如式(2)(3)所示

PTXsZs=PTXt，

(2)

(PTXs)T=Zt(PTXt)T.

(3)

式中：Zs∈Rns×nt是作用于源域的表示矩陣；Zt∈Rns×nt是作用于目的域的表示矩陣；Xt∈Rm×nt是目的域的樣本，nt代表目的域樣本的數目.對于分布不同的兩個域，按照各自特征去學習不同的表示矩陣有助于對齊兩個域的分布，同時保存自己特有的信息.

2 表示矩陣的約束設計

共同子空間和合理的兩個表示矩陣可以減小兩個域差異的同時盡可能地保存兩個域的原始有用信息.為了得到盡可能最優的兩個表示矩陣，對上面提出的兩個表示矩陣進行了相應的約束設計，進而借助它們學習到有利于域適應的共同子空間.由于兩個表示矩陣需要保留的特征不同，應該按條件對它們施加不同的約束.在兩個域分布差異盡可能小的公共子空間上，目的域數據通過表示矩陣可以被源域的數據線性表示，如式(2)所示.也就是說，目的域中的每個樣本都可以視作是源域樣本的線性組合.再則考慮到源域的數據具有可靠的標簽，對源域表示矩陣進行按列稀疏約束，表示為

(4)

式中‖·‖1表示1-范數.這樣目的域的樣本可以由更少的源域樣本線性組合，保留了數據局部結構的同時能夠更確切地分類.

但是同一類別往往有很多樣本，當某一個樣本由同一類樣本線性組合表示的時候并不會丟失可判別性，反而會提高可判別性并降低過擬合的風險.受這個思路和最優傳輸理論[18]的啟發，本文采用group-lasso作為Zs表示矩陣的稀疏約束，對表示矩陣按類別進行稀疏約束，同一類別采用2-范數降低稀疏約束強度，表示為

式中，‖·‖2表示2-范數，τcl是源域第cl類數據對應表示矩陣Zs中相應行的組合，j代表樣本特征維度的第j維.綜上，源域表示矩陣Zs受到的稀疏約束由式(4)改進為式(5).

(5)

為了更好地保留數據的結構信息，最理想的情況是源域中相同類別的數據被目的域中的數據用同一種線性表示方式所表示.例如作用在目的域的表示矩陣的秩降低到等于類別數，即說明同一類樣本擁有同樣的線性表示方式.于是作用于目的域的表示矩陣應該受到低秩約束，如式(6)所示

(6)

將式(1)～(3)、(5)和(6)合并，得到最終的模型，總模型為

(7)

其中，α和β是超參數. 總模型示意圖如圖1所示.

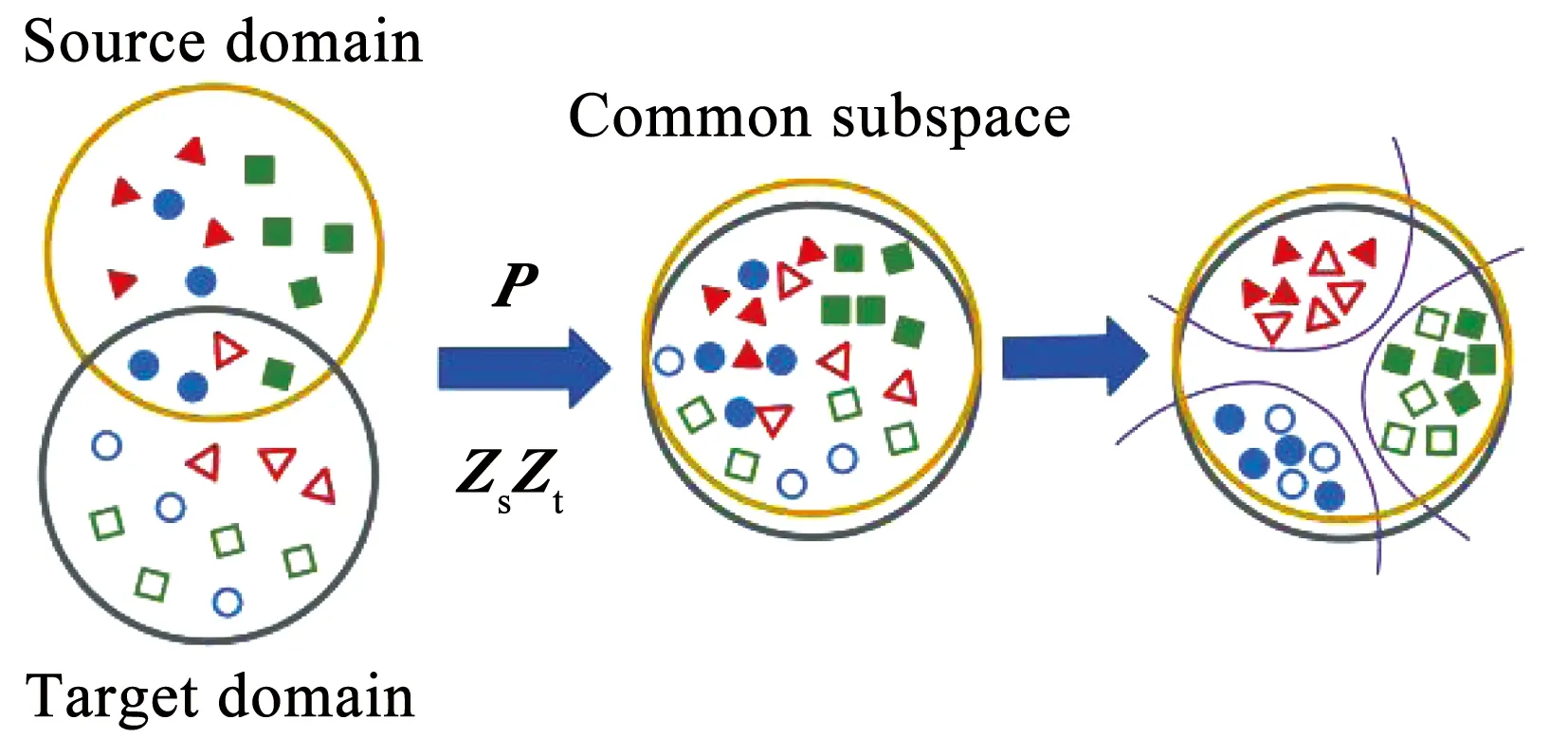
圖1 模型示意

3 模型求解

式(7)的最優化問題是非凸的，求解只能保證局部最優而不是全局最優.為了解決這個問題,利用不精確拉格朗日乘子法(IALM)將該問題轉換成凸問題，轉換如下：

(8)

可以通過增廣拉格朗日乘子法，進一步將式(8)轉換為

β‖Z1‖*+α‖Z2‖group-lasso+

〈Y1,PTXsZs-PTXt〉+

〈Y2,(PTXs)T-Zt(PTXt)T〉+

〈Y3,Zt-Z1〉+〈Y4,Zs-Z2〉+

(9)

式中，μ是懲罰參數；Y1、Y2、Y3和Y4代表拉格朗日乘子，在優化求解過程中，每次更新其中一個變量并固定其余變量迭代求解.

4 理論分析

Ben-David[19]定理提出源域分類器在目的域中的誤差上限，即借助源域有標簽的樣本訓練得到的分類器來識別無標簽的目的域樣本的誤差上限.如式(10)所示

minEDS[|fS(X)-fT(X)|],

EDT[|fS(X)-fT(X)|].

(10)

由于標簽函數是已知的，所以minEDS[|fS(X)-fT(X)|],EDT[|fS(X)-fT(X)|]是一個常量.從式(10)可以推出，若需減小目的域分類誤差，則需要減小S(h)和d1(DS,DT).所以域自適應算法的關鍵是在保證源域誤差盡可能小的同時減小兩個域之間的差異.本文模型中的式(1)就是利用源域的可靠真實標簽來減小S(h).同時通過式(2)和(3)構建了兩個域之間的關系，然后提出最優化約束設計來減小兩域的差異，減小d1(DS,DT).相較于目前其他域自適應算法，所提算法使兩域可以最優地相互表示，從而降低過擬合以及破壞兩域基本結構的風險.

5 實 驗

在3個遷移學習常用的數據集上開展實驗進行驗證.1)COIL20數據集將1 440張灰度圖片分成了兩個域：COIL1(C1)和COIL2(C2).該數據集的樣本有20個類別，COIL20數據集的部分示例見圖2.2)Office-Caltech 10[10]是最廣泛使用的數據集，一共分為4個域：Caltech(C)、Amazon(A)、DSLR(D)和Webcam(W) .本文的實驗使用了該數據集800維的SURF特征和4 096維的DeCAF特征.3)ImageCLEF-DA[16]由3個數據集共同的12類數據組成，3個數據集分別是：Caltech-256(C)、ImageNet ILSVRC 2012(I)和VOC 2012(P).可構建6個跨域任務：C→I、C→P、I→C、I→P、P→C和P→I.

圖2 COIL20數據集部分示例

與以下10種傳統遷移學習方法進行了對比，包括：TCA[6]、GFK[14]、JDA[8]、SA[11]、DTSL[16]、CORAL[20]、BDA[21]、DICD[22]、KOT[23]和DST-ELM[24]，同時還與以下2種深度方法也進行了對比：AlexNet[25]和JDOT[26].實驗結果見表1～5，其中識別準確率的最好值與次好值分別通過加粗和下劃線表示.從實驗結果來看，本文的方法超過了很多的傳統遷移學習方法和一些深度方法，其中包括一些比較先進的傳統遷移學習方法如DST-ELM和深度方法如JDOT等，這體現了本文方法的有效性.

5.1 實驗結果及分析

在COIL20數據集構建兩個跨域任務：COIL1→COIL2和COIL2→COIL1.其中，COIL1由角度為[0°,85°]∪[180°,265°]的灰度圖像組成，而COIL2則由[90°,175°]∪[270°,355°]的灰度圖像組成.實驗結果如表1所示，本文算法的平均準確率達89.3%,比CORAL準確率高了7.3%.JDA簡單地考慮邊緣分布和條件分布適配反而比DTSL和CORAL效果好.由于兩個域的差異僅僅來自圖片的拍攝角度不同，所以該任務比其他數據集簡單，過度擬合和破壞源域的基本結構反而會降低在該數據集的識別準確性.而本文采用group-lasso作為表示矩陣的稀疏約束，可以降低過擬合風險，從實驗結果可以驗證本文模型的有效性和魯棒性.

表1 在COIL20數據集上的準確率

在Office-Caltech 10數據集上，不論使用SURF特征還是DeCAF特征，本文算法都超過了對比的算法.采用SURF特征的平均準確率為51.2%，使用DeCAF特征，本文模型的平均準確率達90.6%，分別如表2和表3所示.與DTSL對比，使用SURF特征，本文模型的準確率提升了4.5%，如果使用DeCAF深度特征，本文模型將準確率從83.8%提升到了90.6%.由于DTSL只使用了一個表示矩陣，對源域的基本結構造成了一定的破壞，很難保存所有目的域的有用信息.所以本文模型采用兩個表示矩陣解決了相關問題，從而提升了準確率.DICD通過MMD測量來減小兩個域之間的差異，雖然考慮了減小類內距離和擴大類間距離，但是只通過MMD距離來判斷差距也會對結構造成一定的破壞，本文算法在這個數據集上的效果仍然高于DICD，這也驗證了本文算法具有不錯的可判別性.

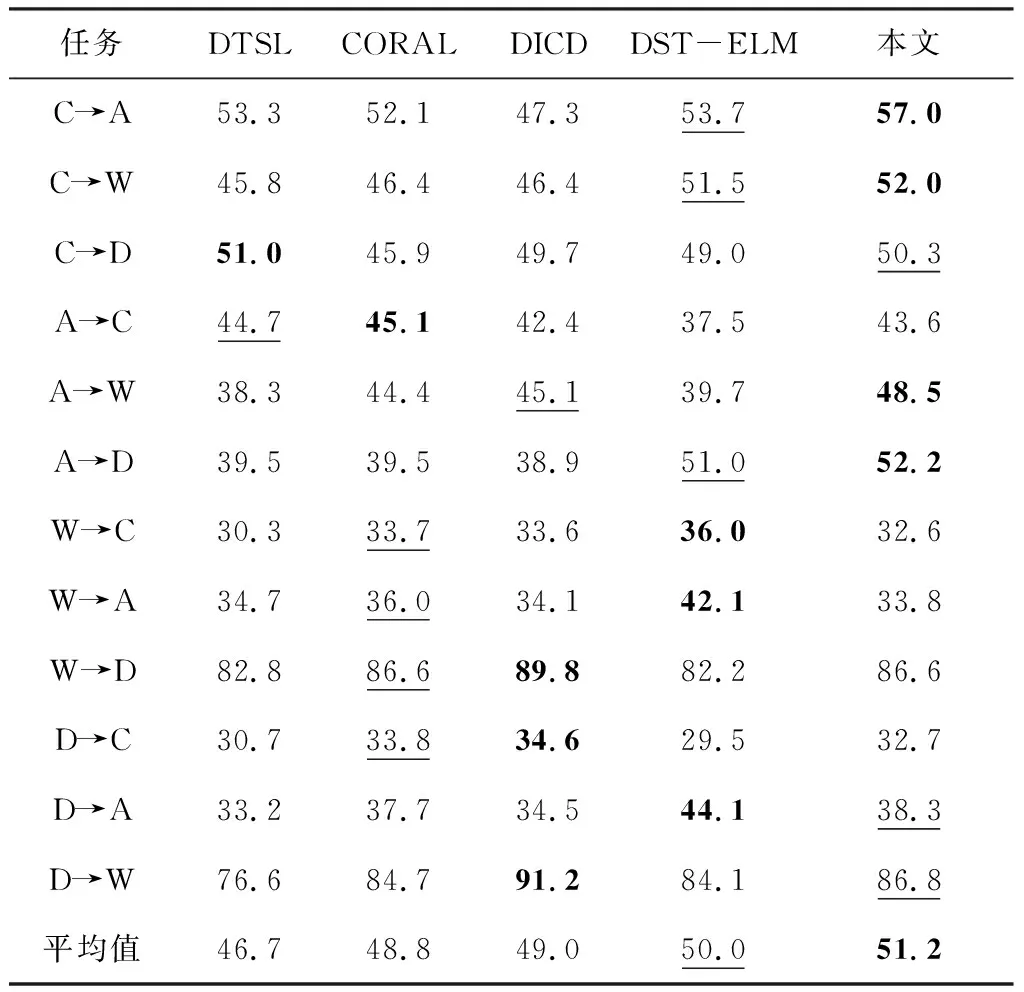
表2 在Office-Caltech 10 (SURF) 數據集上的準確率

表3 在Office-Caltech 10 (DeCAF) 數據集上的準確率

傳統的方法在Office-Caltech 10數據集使用DeCAF特征都取得了不錯的結果.雖然本文的方法與一些先進的傳統方法(如DST-ELM)對比只提升了一點，但是與某些先進的深度方法(如JDOT)做對比時，本文的方法仍能顯示出一定的優勢，如表4所示.

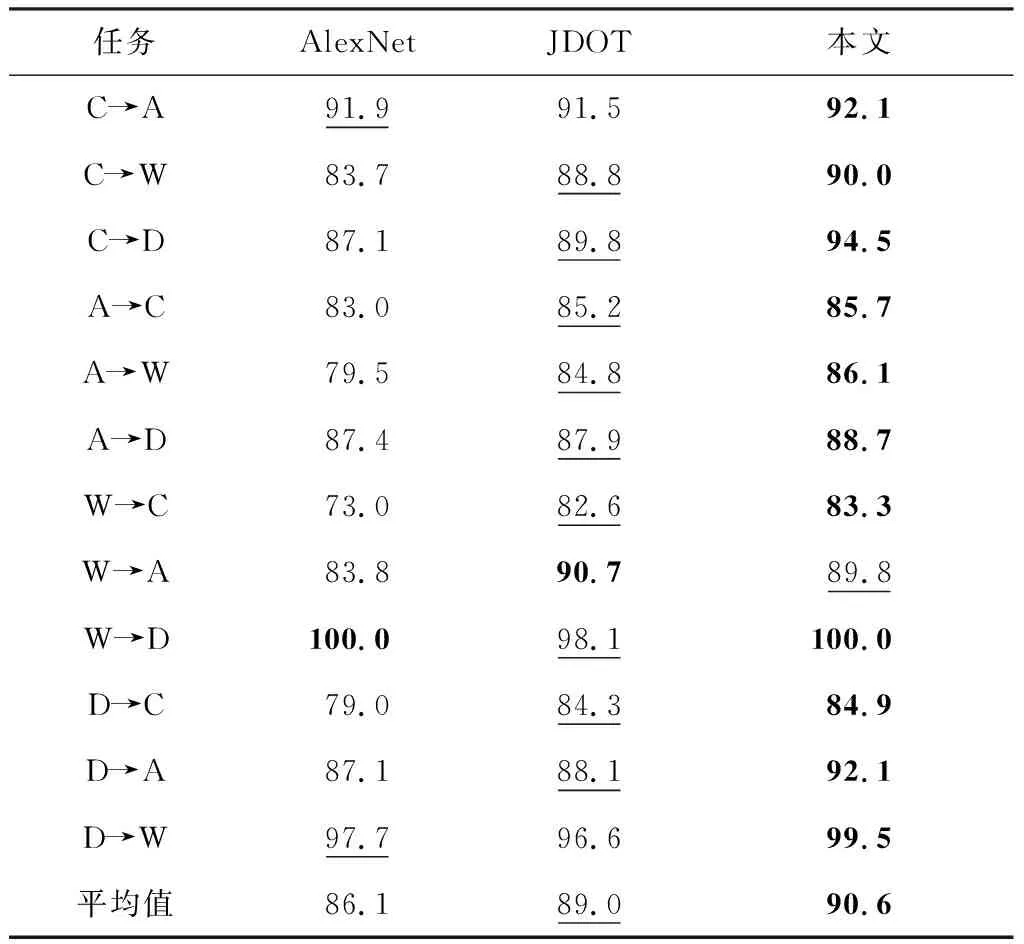
表4 在Office-Caltech 10 (DeCAF) 數據集上與深度方法對比準確率

在ImageCLEF-DA數據集，使用ResNet50網絡提取的深度特征.顯然，本文算法的效果優于所有對比的算法.實驗結果如表5所示.

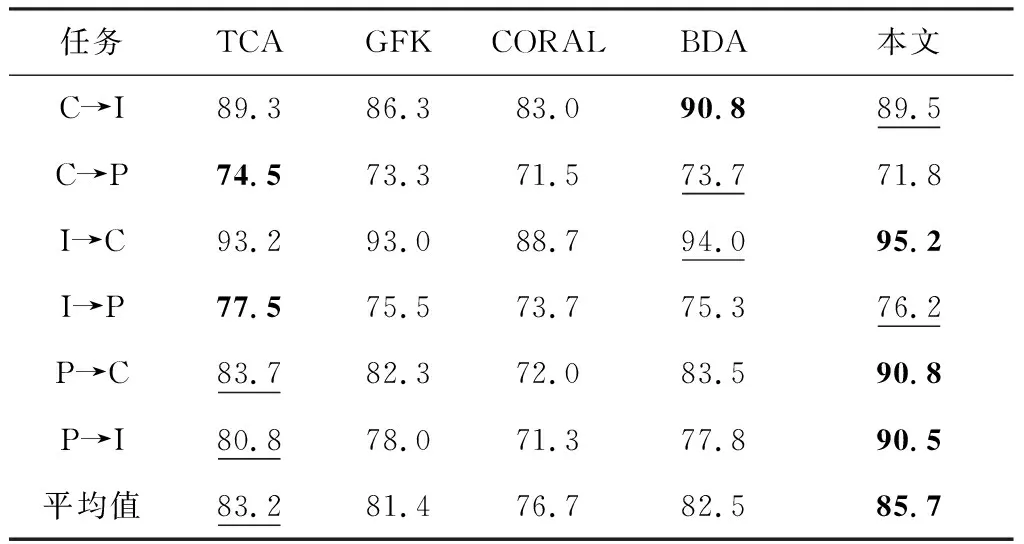
表5 在ImageCLEF-DA數據集上的準確率

5.2 消融分析

為了進一步驗證對作用于源域的表示矩陣施加group-lasso約束是否可以提高模型的識別準確率，進行了消融實驗.RLlow-rank模型只對Zt矩陣進行低秩約束，對Zs矩陣不做約束.RLsparse模型對Zs矩陣做1-范數稀疏約束.RLgroup-lasso模型對Zs矩陣采用group-lasso約束.RLjoint1模型對Zs和Zt兩個表示矩陣分別做1-范數和低秩約束，而RLjoint2模型對Zs和Zt兩個表示矩陣分別做group-lasso和低秩約束.實驗結果如表6所示.通過對比RLgroup-lasso和RLsparse兩個模型的實驗結果，可以明顯得出在域自適應表示學習中，稀疏約束采用group-lasso優于使用1-范數.通過RLjoint1的實驗結果，僅僅對作用于源域的表示矩陣Zs采用group-lasso約束的分類準確率甚至高于同時使用1-范數和低秩約束.對比RLgroup-lasso和RLjoint2模型的實驗結果，對Zt的低秩約束也是必不可少的，能夠更好地保留樣本特征的結構，從而提高準確率.

表6 Office-Caltech 10 (SURF)數據集上消融實驗的結果

5.3 參數敏感度分析

由式(7)可知，本文的總模型含有兩個超參數α和β.為了分析不同參數對模型識別準確率的影響，在COIL20、Office-Caltech 10和ImageCLEF-DA 3個數據集進行了參數敏感度實驗：在離散數據集[0.001, 0.01, 0.1, 1, 5, 10]的范圍內改變兩個超參數的值，觀察識別準確率的變化，實驗結果見圖3.從圖3可以觀察到，參數α和β的取值在0.001～10大范圍變化，對識別準確率造成的影響依然很小.所以雖然本文的模型需要調試兩個超參數，但是兩個超參數的選擇卻較簡單，在相對大的范圍內取值，都可以使本文的模型分類準確率達到一個很好的效果.

圖3 參數敏感度分析

6 結 論

針對無監督域自適應問題，本文提出了一個新穎的表示學習算法.為了在學得的共同子空間下更好地保留源域和目的域樣本的特有特征和結構，使用兩個不同的表示矩陣分別作用于兩個域，同時基于線性表示和最優傳輸相關理論為這兩個表示矩陣設計不同的約束.大量的實驗驗證了本文模型的有效性和魯棒性，在多個數據集上，本文方法的識別精度超過了很多先進的無監督域自適應方法.