盤型懸式絕緣子瓷件的應力分析和結構優化
張廼龍,劉 洋,高 嵩,陳 杰,荊宇航
(1.國網江蘇省電力有限公司 電力科學研究院,南京 211103; 2.哈爾濱工業大學 航天科學與力學系,哈爾濱 150001)
中國將特高壓工程列入國家“十二五”規劃,計劃建設“三橫三縱一環網”特高壓骨干網架.這一過程中,中國的特高壓輸電在電壓等級、輸送電量、距離等方面不斷刷新世界紀錄.絕緣子作為特高壓輸電線路的重要組成部分,是保證線路穩定運行的重要部件,隨著國家的特高壓工程、西電東送工程等的建設,絕緣子的需求隨著國家電網的建設日益增大[1-3].
絕緣子的運行過程受到風載、雨雪、冰凍、溫差等復雜戶外環境的影響,同時也承受電場強度以及機械載荷等多種因素的共同作用.絕緣子在運行過程中,時常出現瓷件斷裂、絕緣子掉串等事故,冬季低溫環境使金屬附件應力收縮、水泥膠合劑長期凍結都會引起事故的發生.另外,在絕緣子的生產和安裝過程中,常常造成絕緣子表面劃痕甚至微小裂紋等損傷,使得絕緣子在運行時,在機械載荷的作用下,裂紋處發生應力集中,使裂紋進一步擴展,從而導致絕緣子的斷裂[4-8],這給輸電線路的安全穩定運行帶來了極大的隱患.
盤型懸式絕緣子在工作狀態下,要承受來自導線張力所決定的拉力載荷,因此本文重點研究絕緣子在拉力載荷作用下,瓷件上的應力分布情況.通過對絕緣子在不同拉力方向下的應力分布進行計算,對絕緣子的安裝提供可行的建議,并在拉力的作用下,對絕緣子進行結構優化,來改善絕緣子瓷件上的應力集中情況.
1 盤型懸式絕緣子的有限元建模
1.1 盤型懸式絕緣子的基本結構分析
盤型懸式絕緣子的基本結構包括瓷件、鋼腳、鐵帽和水泥膠合劑.瓷件表面一般上白釉;鐵帽和鋼腳與水泥膠合劑接觸表面薄涂一層緩沖層;鐵帽與鋼腳通常使用鑄鐵作為材料,二者表面全部鍍鋅,達到固定和連接的作用;水泥膠合劑使瓷件與鐵帽、鋼腳構成一個機械和電氣的結構整體,起到膠裝結構的作用[9-11].本文主要針對用于架空線路的線路絕緣子,盤型懸式絕緣子在工作時成串掛網.在工作狀態下,絕緣子主要承受拉力和重力.420 kN盤型懸式絕緣子的主要幾何尺寸見圖1.
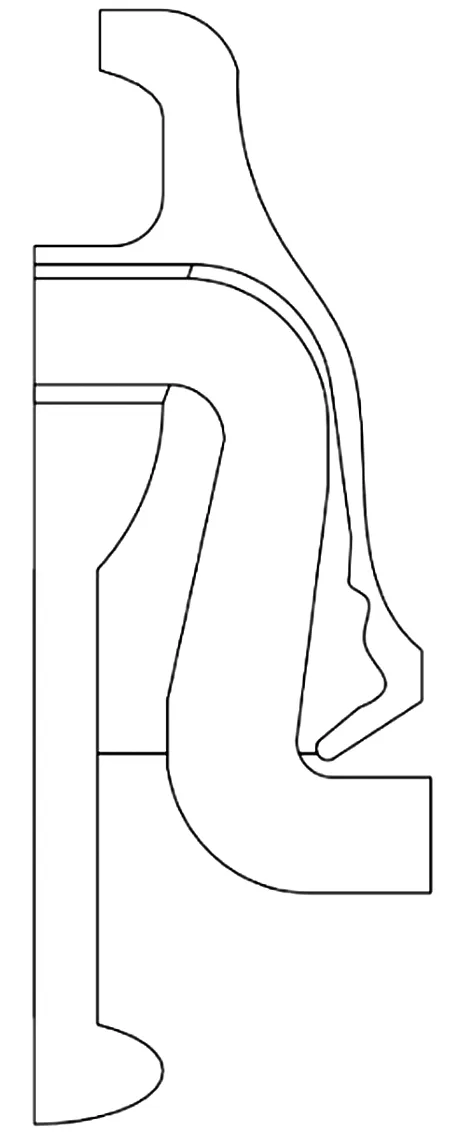
圖1 絕緣子幾何結構示意
1.2 盤型懸式絕緣子的有限元仿真模型
通過有限元軟件ABAQUS,建立盤型懸式絕緣子的三維有限元模型.由于在實際中,盤型懸式絕緣子的結構對稱,體積相對較大,故將模型簡化為5個部分,從上到下依次為鐵帽、水泥膠合劑(膠結鐵帽和瓷件)、瓷件、水泥膠合劑(膠結鋼腳和瓷件)以及鋼腳[12-13].由于盤型懸式絕緣子球窩部分的連接結構尺寸是標準規定的,且不是本文所要研究的重點,因此可以將其在有限元模型中簡化為鐵帽結構.由于盤型懸式絕緣子的傘裙部分應力水平較低(后面的計算結果可以證明),為提高計算效率,建模時將此部分刪除.建模中采用的長度單位為mm,力的單位為N,應力的單位為MPa,相關材料的主要性能參數見表1.
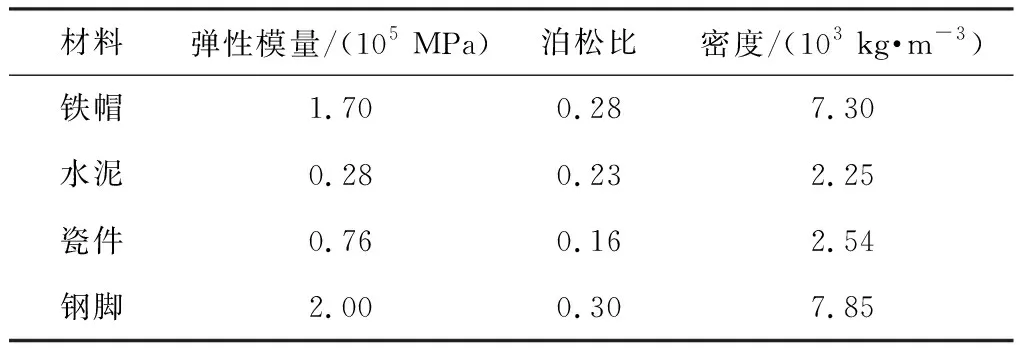
表1 材料參數
將材料參數分別賦予絕緣子的各部件.使用C3D8R單元和C3D10單元來劃分網格,絕緣子模型共有51 881個節點和32 300個單元.
將盤型懸式絕緣子各部件裝配到一起,設置其相鄰部件之間的相互關系.將瓷件的表面和與之接觸的內外層水泥膠合劑之間的相互關系設置為面面接觸,且取摩擦系數為0.35,將內外層水泥膠合劑分別與鋼腳、鐵帽設置為綁定約束.盤型懸式絕緣子的三維有限元模型見圖2.

圖2 絕緣子有限元模型
2 不同載荷工況下絕緣子的應力分布
2.1 絕緣子在拉力載荷作用下的應力分布
由于盤型懸式絕緣子的瓷件為陶瓷材料,是典型的脆性材料,其抗拉性能要比抗壓性能差很多.絕緣子在工作狀態下,主要承受拉力外載荷作用,絕緣子的有限元模型的結構較大,不利于查看某一點的應力值,所以選擇瓷件上Mises應力的最大值為研究對象,以此來分析數據結果以及對盤型懸式絕緣子進行結構優化.
對絕緣子鐵帽上方的連接面施加面力,大小為60 MPa,以此來等效拉力載荷作用.對絕緣子鋼腳的底部施加固定約束,即
U1=0,U2=0,U3=0,UR1=0,UR2=0,UR3=0.
瓷件上的Mises應力分布情況見圖3.

圖3 瓷件的Mises應力分布和拉伸破壞
由圖3可知,瓷件中間部位的應力水平較高,在頂部拉力的作用下,導致瓷件與水泥膠合劑的接觸面部分分離,只在瓷件中間部位的接觸面未發生分離,兩者之間的作用力僅靠此處的接觸面傳遞,從而導致瓷件在此處的應力水平較高.在絕緣子的拉伸實驗中,瓷件的破壞從中間位置開始,最終發展為整個瓷件的斷裂,為仿真結果進行了驗證.因此在絕緣子的膠裝過程中,應加強瓷件與水泥膠合劑的膠裝強度,使瓷件上的應力分布更加均勻,有效增加絕緣子的工作壽命.
2.2 絕緣子在不同拉力方向下的應力分布
對絕緣子施加不同方向的力載荷,以模擬分析由于施工安裝的不合理所造成的絕緣子在受力方向不確定的情況下的應力分布.建立絕緣子的三維結構,集中力載荷作用在絕緣子的頂部,作用力大小不變,為10 kN,方向與絕緣子軸線的夾角從0°到80°變化,選取夾角的角度變化幅度為10°.在不同的受力方向下,絕緣子瓷件上最大應力的變化如圖4所示.
從圖4中可以得到,當集中力的方向從0°到80°變化時,絕緣子瓷件結構的應力值隨之增大.因此在絕緣子的安裝中,應該使絕緣子的受拉方向與軸線的夾角盡可能的小,從而減小絕緣子瓷件的應力水平,有效防止斷裂事故的發生.
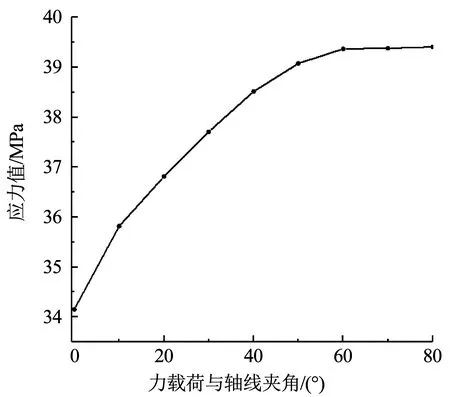
圖4 不同角度下的應力
3 基于機器學習的絕緣子結構優化
3.1 參數化建模
對絕緣子有限元模型進行參數化建模,并對絕緣子的幾何結構參數進行調整,生成大量不同結構的模型,通過ABAQUS的計算,得到各個結構的最大應力.考慮到絕緣子的失效主要是由瓷件的破壞所引起的,因此對瓷件以及與瓷件接觸的水泥膠合劑進行參數化,通過對這些相關參數的調整,改變絕緣子的結構[14-15],由ABAQUS計算得到對應結構的應力分布.
通過對絕緣子參數化模型的計算,得到大約600組不同結構絕緣子的節點坐標和相應的應力值,以此來進行后續機器學習的工作.
3.2 機器學習
3.2.1 神經網絡模型
神經網絡學習方法對于逼近實數值、離散值或向量值的目標函數具有很強的魯棒性,是一種普遍而且實用的機器學習算法.神經網絡的主要思想是前向傳播和反向傳播算法.在前向傳播過程中,數據由輸入層輸入,然后經過若干層隱藏層的處理,最終由輸出層輸出.此時將輸出層輸出的預測值與真實值進行誤差計算,如果誤差較大,則會進入反向傳播過程.在反向傳播過程中,神經網絡會對各層之間的權重與偏置項進行調整,接著再進入前向傳播過程,使預測值與真實值誤差減小.反復循環,不斷地調整權重和偏置項,使預測值在誤差允許的范圍內達到要求,隨即停止訓練.
本文選擇全連接層神經網絡作為神經網絡結構[16-19],全連接層神經網絡是一種按誤差傳播算法訓練的多層前饋網絡,能學習訓練大量輸入輸出映射關系,具體結構見圖5.
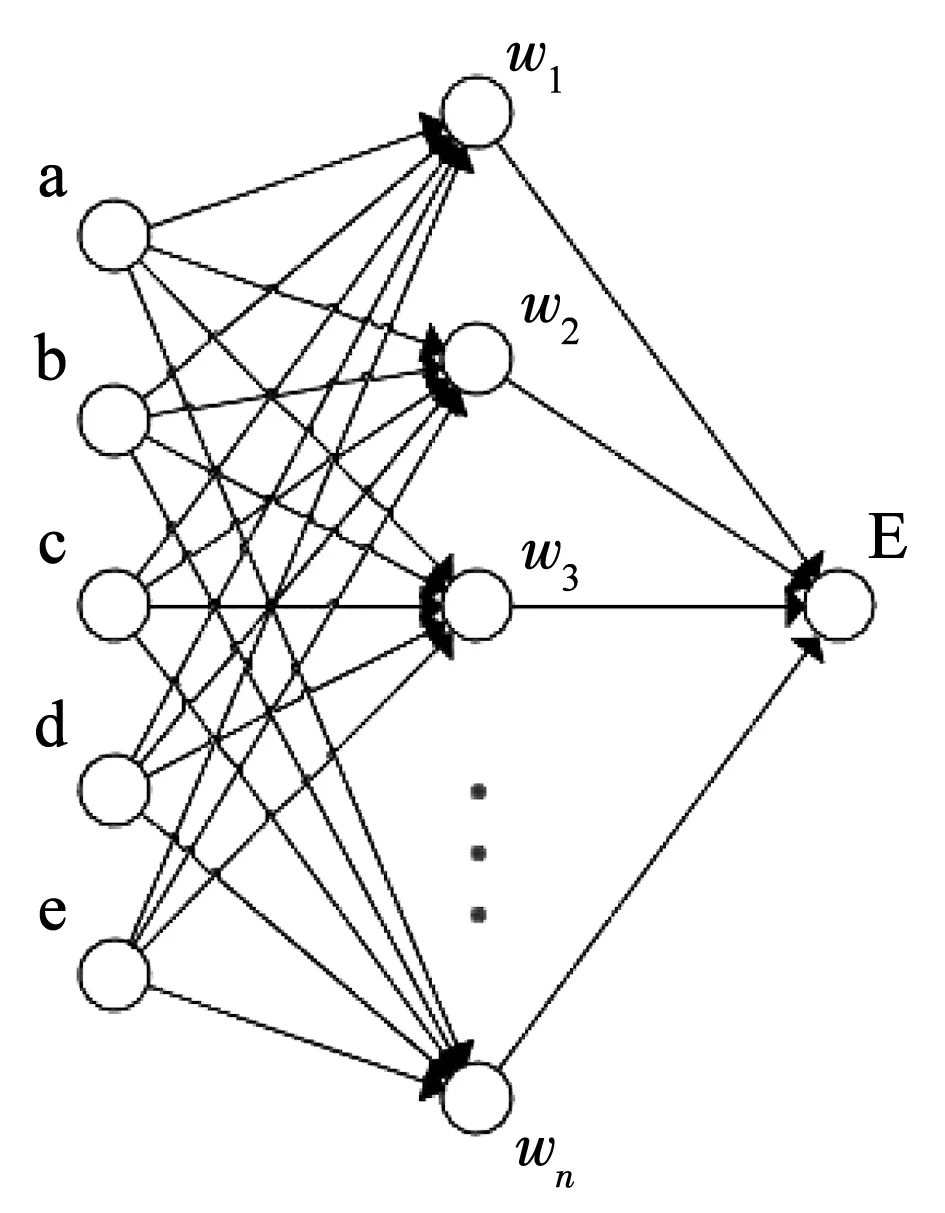
圖5 神經網絡結構
該模型中絕緣子瓷件上的5個坐標值為輸入向量,絕緣子瓷件最大Mises應力為輸出向量,w1、w2、wn為權重系數,從而構建一個3層全連接神經網絡.
3.2.2 激活函數的選擇
在神經網絡中,常通過加入激活函數實現去線性化,常用的激活函數主要有ReLU函數、sigmoid函數、tanh函數,因為sigmoid函數與tanh函數一般會帶來梯度消失的問題,增加梯度的不穩定性,所以本文選擇ReLU函數.ReLU激活函數相對前兩者收斂更快,誤差可以很好地傳播,權重可以正常地更新.輸入層的輸入與輸出都是樣本集的屬性值,隱含層和輸出層的輸入為
(1)
式中:ωij是單元i和單元j之間的權值,xi是單元i的輸出,θj是單元j的閾值.
經過激活函數的處理,得到隱含層的輸出為
xj=max(0,Sj).
(2)
3.2.3 損失函數的選擇
評價機器學習好壞的指標之一是損失函數的大小.機器學習常使用的損失函數有交叉熵與均方誤差,由于本次研究的問題屬于回歸問題,所以使用均方誤差[20-21].全連接層神經網絡的主要目的是反復修正權值和閾值,使得誤差函數值達到最小,誤差函數為
(3)
式中,dj為輸出層的期望結果,yj為輸出層的實際結果.
3.2.4 學習率的選擇
在神經網絡中,學習率決定了損失函數下降的速度,學習率的選擇不宜過小,也不宜過大,為了使結果更好地收斂,選取合適的學習率至關重要.本次模型選取0.01、0.001、0.006這3種學習率進行調試,從中選取最優的學習率[22-23].經過調試,學習率為0.01與0.006時的損失函數要小于學習率為0.001時的損失函數,保守起見選擇0.006作為學習率,以防止隨著訓練次數的增加造成損失函數出現大的波動現象.
3.2.5 正則化率的選擇
在神經網絡中,需要正則化項來消除過擬合問題.正則化項的大小通常是由正則化率來調節,本文模型選取0.000 000 01、0.000 001、0.000 1這3種正則化率進行調試.經過調試,正則化率為0.000 000 01與0.000 001時的損失函數要小于正則化率為0.000 1時,故兩種正則化率都可以選取,本文選取0.000 000 01為正則化率.
3.3 模擬結果及誤差分析
3.3.1 模擬結果
取神經網絡的隱藏層節點個數為50,訓練次數為210 000.取16組原始數據作為測試集,并將訓練結果、測試結果與真實結果分別擬合,見圖6.
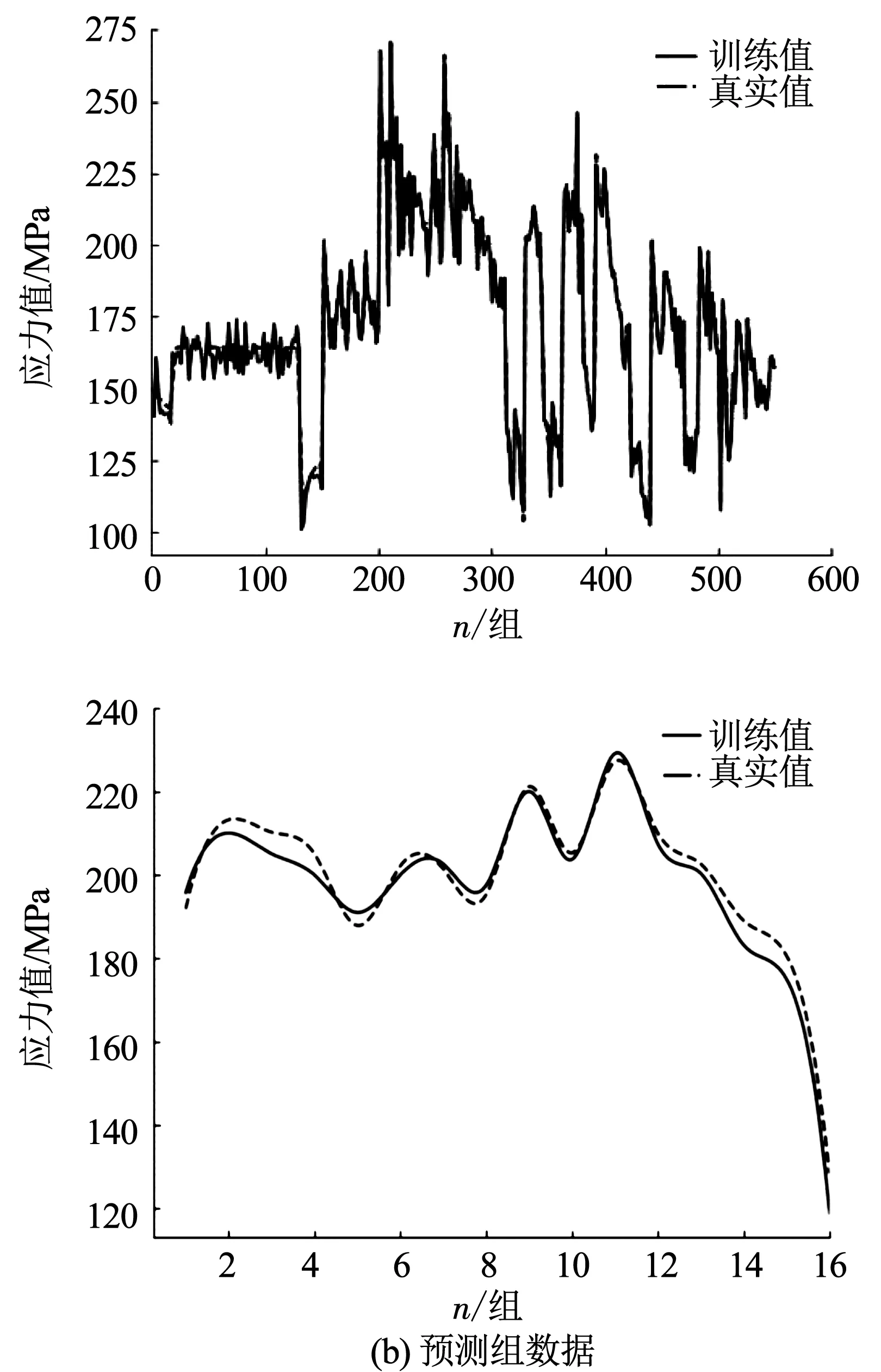
圖6 訓練值及預測值與真實值的曲線圖
從圖6(a)中可以得到,前100組數據的真實值在訓練值上下來回震蕩,震蕩范圍大約為10 MPa,但是后100組數據上訓練值與真實值基本完全擬合.訓練數據的平均誤差在3.3 MPa左右,已經完成較好的擬合情況.
另外取出原始數據的16組數據作為測試集在最終的機器學習模型上進行測試,將測試得到的最大Mises應力的預測值與真實值用曲線擬合,見圖6(b).從圖中可以得出,測試值與真實值之間的軌跡基本擬合,該模型可以對結果做出合理預測.
將112 000種絕緣子瓷件結構的坐標信息放在上述的機器學習模型中進行預測,并將預測結果按照升序排列,得到不同結構的絕緣子瓷件的最大Mises應力見圖7.從模擬結果可以得到,絕緣子瓷件的最大Mises應力的最小值為107.233 MPa.
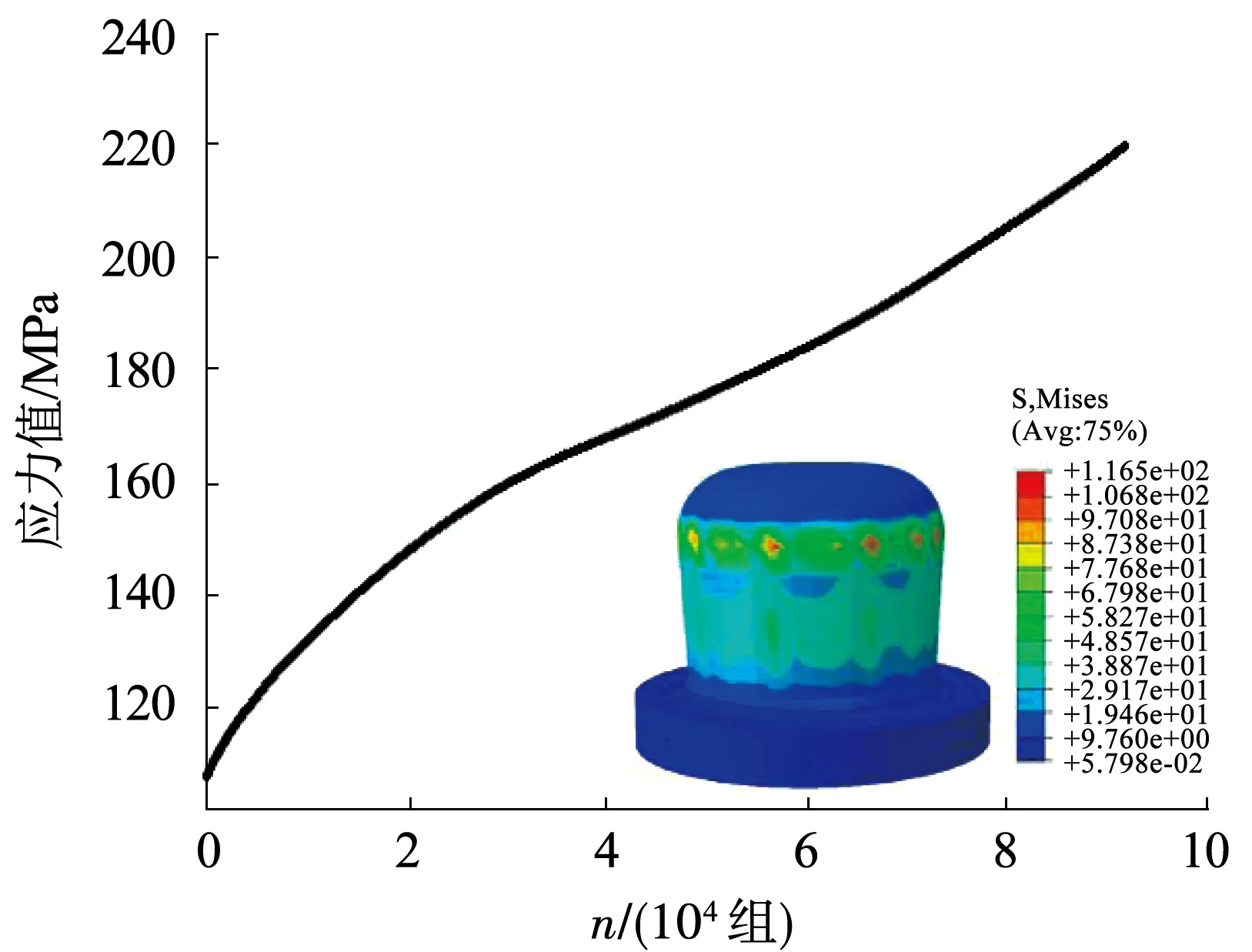
圖7 預測值與最優應力情況
3.3.2 誤差分析
將機器學習預測得到的最大Mises應力的最小值所對應的結構坐標在ABAQUS中進行建模運算,得出的最小值的真實值為107.924 MPa,與機器學習預測的值相比,誤差率僅為0.644%,說明機器學習模型的可靠度較高.優化之前,原始結構的瓷件上的最大應力為155.508 MPa,優化效果顯著,可以按照該優化結果作為新的結構進行設計生產.
優化前后的結構對比如圖8所示,其中實線圖形為原結構示意,虛線圖形表示優化后部分結構改變后的位置.
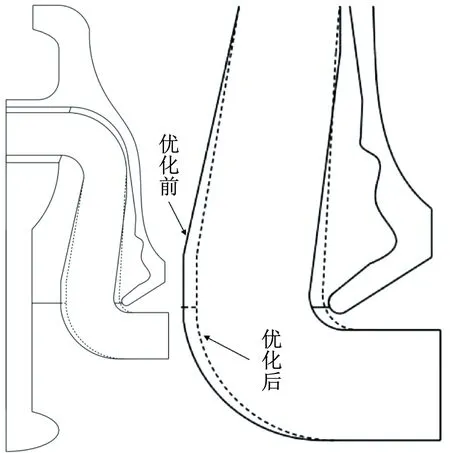
圖8 優化前后結構對比
4 結 論
1)絕緣子在拉力作用下,瓷件和水泥膠合劑發生部分接觸面分離,導致瓷件未分離的中間部位的應力水平較高,因此應加強絕緣子的膠裝強度,以使瓷件上的應力分布更加均勻.
2)絕緣子在不同的受拉載荷作用下,當拉力方向與軸線的夾角越大時,瓷件上的應力水平越高.為使絕緣子安全運行,在絕緣子的安裝中,應該使絕緣子的受拉方向與軸線的夾角盡可能的小.
3)采用機器學習和有限元計算相結合的方法,通過大量ABAQUS計算得到不同結構以及相應的最大應力值,調試得到機器學習模型,利用這一機器學習模型可以快速且準確地預測不同絕緣子結構的最大應力值.預測得到最優結構之后,再利用ABAQUS對最優結構進行有限元計算驗證,發現兩者誤差率僅為0.644%,且最優結構較原始結構應力水平降低了30%,優化效果顯著.

