考慮雙側不確定性的負荷聚集商需求響應資源規劃

張 鵬，蒯圣宇，劉 維，張如鵬，汪大為，楊 洋，王振宇

（1. 國網安徽省電力有限公司 肥東縣供電公司，合肥 231600；2. 國網安徽省電力有限公司，合肥 230022；3. 國電南自自動化有限公司 上海分公司，上海 201319；4. 國網山東省電力公司 臨沂供電公司，山東 臨沂 276003）

0 引言

隨著需求響應（demand response，DR）項目逐漸市場化和商業化［1］，作為整合零散電力需求側資源的專門機構，負荷聚集商（load aggregator，LA）近幾年在國內試點城市逐步發展起來［2］，受到了極大關注。負荷聚集商（下文簡稱聚集商）的出現為小型需求側用戶參與需求響應項目提供了機會，增強了需求響應的社會效益［3］。

關于聚集商的初期研究多集中于其運營機制和調度策略等方面。文獻［4］基于Stackelberg 策略設計了微網聚集商與配網運營商之間競爭的博弈模型，使得零售市場所有參與者的運營利潤最大化。文獻［5］通過用戶調度潛力分析，提出基于聚集商模式的冰蓄冷空調棄風消納方法。文獻［6］提出了對于需求響應資源具有靈活控制策略的聚集商日前能量市場投標方案。文獻［7］在文獻［6］的基礎上計及電價的波動性，提出了聚集商市場投標的隨機優化方法。

然而，考慮到不確定風險因素，當前關于聚集商用戶側資源配置規劃的研究較少。文獻［8］研究了聚集商在參與可中斷負荷項目中的成本效益，但沒有考慮到投資過程中的風險問題。文獻［9］提出了考慮用戶違約可能的儲能配置策略，但沒有考慮市場側電價的不確定因素。當前，條件風險價值（conditional value at risk，CVaR）理論已廣泛運用于微電網［10］、增量配電網［11］及綜合能源經濟調度［12］等研究的風險度量中。

本文在當前研究的基礎上，闡述市場環境下聚集商面臨的雙側不確定性:市場電價以及用戶響應行為。考慮到所述雙側不確定性，建立聚集商的需求響應資源規劃模型，并在模型中引入CVaR 項以量化投資風險。通過分析不同風險偏好對聚集商需求響應資源規劃結果的影響，探討投資收益與風險的權衡，為國內聚集商的規劃和建立提供了良好的參考。

1 聚集商運營模式與雙側不確定性

聚集商作為需求響應專業機構，在原本用戶側需求響應資源數量一定的條件下，其負荷聚集行為降低了需求響應市場的準入門檻，使得原本數量眾多的小容量零散用戶參與到需求響應項目中來，增大了需求響應的規模和效益，體現了顯著的規模經濟。電力市場環境下，聚集商向下與用戶簽訂響應協議以獲取響應資源，同時為協議用戶安裝智能電能表和通信網絡以建立高級量測體系（advanced metering infrastructure，AMI）［13］，如圖1所示。聚集商向上根據市場實時電價信息進行預測和需求響應投標，參與電力市場交易并獲利。然而在該運營模式下，聚集商既面臨市場電價的不確定性，又需應對用戶響應行為的不確定性。

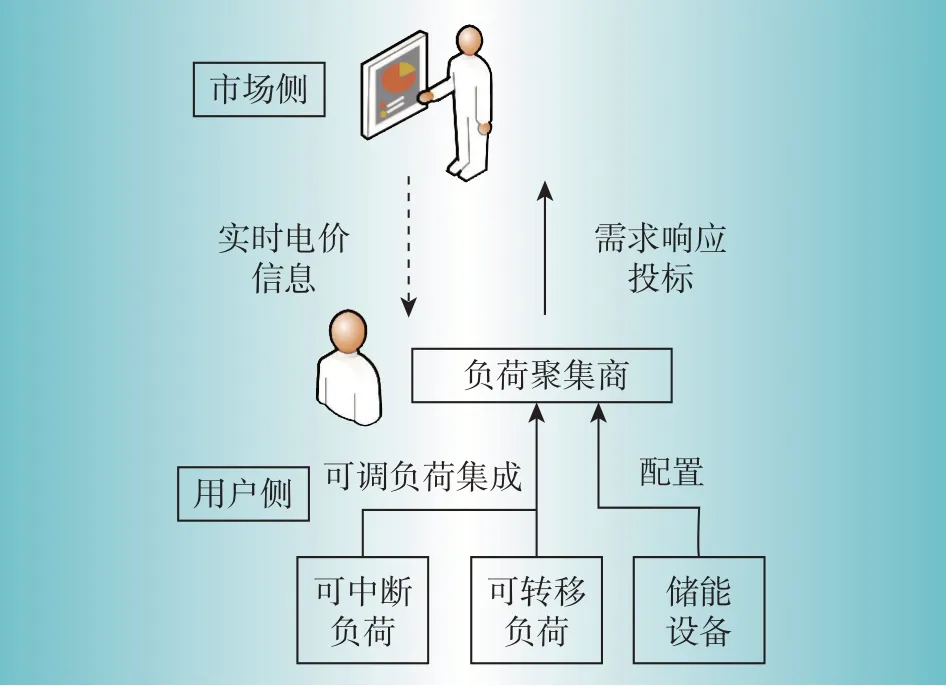
圖1 負荷聚集商的運營框架Fig.1 Operational framework of load aggregators

在市場側，反映短期電能生產成本和供需變化的實時電價具有較大的不確定性。在用戶側，聚集商的需求響應資源從響應機理上可分為可中斷負荷（interruptible load，IL）和可轉移負荷（transferable load，TL）。其中，用戶負荷特性、需求響應意識差異和用戶分散性導致了各類響應資源的成本和不確定性差異。本文中，考慮用戶側可中斷負荷主要由工業負荷（如水泥行業、造紙行業、基礎化工、有色金屬及金屬制造行業等）提供，通常其中斷成本較高，同時響應可靠程度也較高。可轉移負荷主要由居民家用電器等負荷（如洗衣機、熱水器及電動汽車等）提供，由于負荷能夠得到全部或部分的轉移，因此響應補償較低，其響應可靠程度也較低。此外，聚集商可以通過配置一定數量的儲能（energy storage，ES）設備來彌補用戶的不確定行為造成的損失［9］，但當前儲能設備的投資運行成本仍然相對較高。

2 聚集商需求響應資源規劃模型

首先建立聚集商的需求響應日投標模型，在此基礎上，以全年利潤最大化和CVaR度量值最小化為目標，建立聚集商的需求響應資源投資規劃模型。

2.1 需求響應日投標模型

參考文獻［6］將各類用戶側可調負荷和ES作為需求響應資源。聚集商的日投標響應收益為

式中:Rday為日響應投標收益；ρt為t時刻的電價；T為日內可投標時段集合，設定為24 h；Pi,t為聚集商在t時刻投標的第i類用戶側可調負荷或ES的容量；Ω為響應資源集合，包含各類可調負荷和ES；CPi,t為聚集商在t時刻調度第i類用戶側可調負荷或ES的成本。

聚集商投標約束為

式中:ut為聚集商參與投標的0-1 變量，ut=1 表示聚集商在t時段參與需求響應投標，ut=0 則表示聚集商在t時段不參與需求響應投標；為聚集商在集合T內的最大可響應小時數，設定為3 h；為t時段聚集商的最大可投標容量，由實際電價峰谷差決定。

當i為可調負荷時，響應約束包括

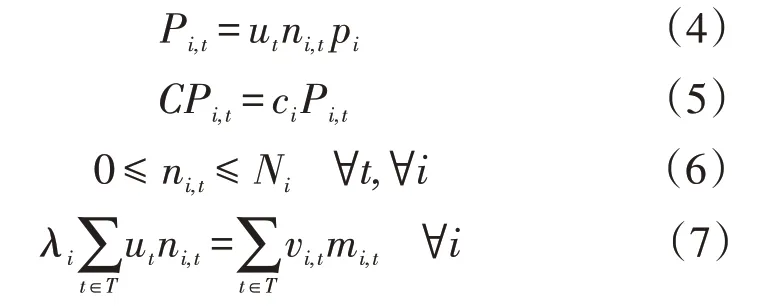
式中:ni,t為聚集商在t時段提供的第i類可調負荷數量；pi和ci為第i類單位可調負荷的響應容量和價格；Ni為聚集商投資規劃的第i類可調負荷資源總數；λi為第i類可調負荷的轉移比例；vi,t為第i類可調負荷被轉移時段的0-1 變量，與ut同理；mi,t為第i類可調負荷被轉移時段的負荷恢復數量。

當i為ES，有充放電約束

式中:為 ES 在t時段的充電功率；pES,max和為單位ES 的最大放電功率和充電功率；wES,t為 ES 充電時段的0-1 變量，與ut同理；ηES為 ES 的充放電效率；EES,max為單位ES的最大存儲電量。

2.2 計及CVaR的需求響應資源規劃模型

實際中，電價歷史數據的獲取較為便捷，而數量眾多的用戶歷史需求響應行為數據在項目發展初期較難獲取。因此，本文采用歷史模擬法處理市場電價的不確定性，采用隨機模擬法描述用戶側資源的響應行為不確定性。以最大化聚集商利潤和最小化聚集商風險為目標，引入CVaR 理論，將CVaR 風險值以一定權重加入目標函數中［11］，得到聚集商年響應目標函數

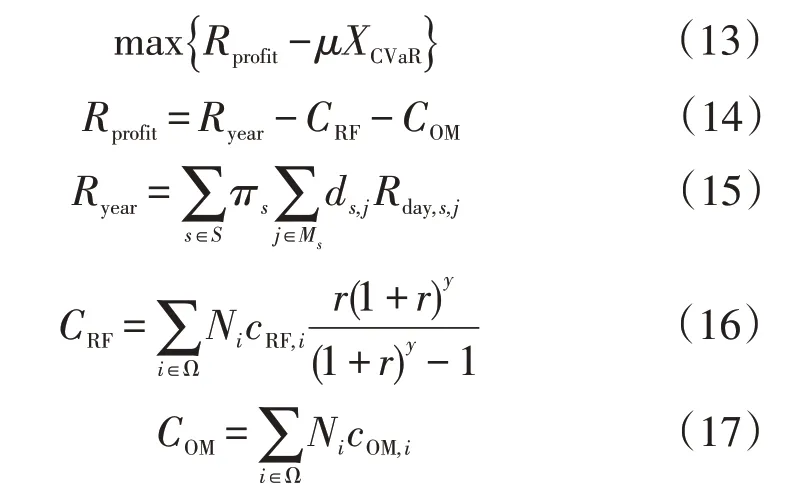
式中:Rprofit為聚集商年響應利潤；XCVaR為CVaR風險度量值；μ為聚集商的風險偏好系數；Ryear為聚集商年響應運行收益；CRF和COM分別為用戶側資源的等年值投資成本和年運行維護費用；πs為第s個計算場景的概率；S為計算場景的集合；Ms為第s個計算場景中的電價聚類場景集合；ds,j為第s個計算場景中第j個電價聚類場景的相似日數；Rday,s,j為第s個計算場景第j個電價場景下的聚集商響應收益；cRF,i和cOM,i分別為第i類用戶側資源的單位投資成本和運行維護成本；r為折現率；y為設備運行年限。

式（13）中，CVaR風險度量項表達式為

式中:XVaR為置信水平β下的VaR值；τs,k為輔助變量；q為隨機模擬的總次數。對于τs,k(k=1，2，…，q)，令，以表示超過XVaR的損失，損失函數f(x,y)取聚集商期望利潤的損失值，為便于計算將其松弛為不等式約束如下

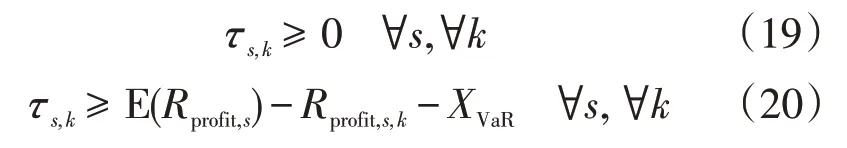
上述優化模型為典型混合整數線性規劃模型，基于Matlab 平臺編程，采用Yalmip 工具箱調用Cplex12.6.1求解器求解，具體的求解流程如圖2所示。

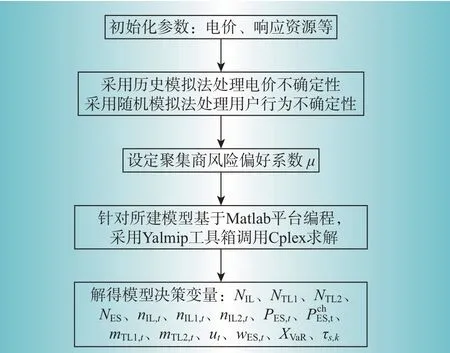
圖2 模型求解流程圖Fig.2 Flowchart for solving the model

3 算例分析

3.1 數據準備

通過對安徽省肥東縣城區部分工業和居民負荷的需求響應潛力進行調研，本算例根據負荷響應成本和不確定性將用戶側可調負荷分為3 類，并將同一區域內具有相同響應特性的電力用戶打包為一組進行響應，單組可調負荷的基本參數見表1。參考文獻［14］，本文ES 采用鉛酸蓄電池組（以120節蓄電池串聯作為一組），單節鉛酸蓄電池的基本參數見表2。響應資源集合Ω={IL,TL1,TL2,ES}。設定折現率r=0.08，置信水平β=0.95。

表1 單組可調負荷基本參數Table 1 Basic parameters of single group adjustable load

表2 單節鉛酸蓄電池基本參數Table 2 Basic parameters of single?cell lead?acid battery

本文選取美國PJM市場2015—2018年實時電價作為歷史數據［15］，并作為4個計算場景，如圖3所示。

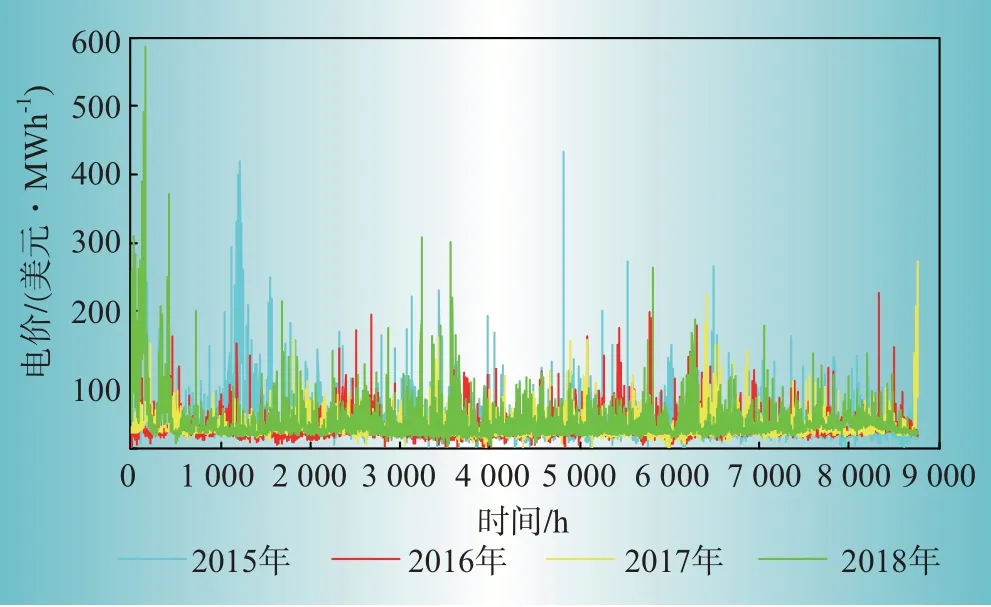
圖3 2015—2018年實時電價數據Fig.3 Real?time electricity price data in 2015—2018

為加快仿真速度，采用k 均值聚類算法分別將各年內日實時電價曲線縮減為4 類。以2016 年為例，電價聚類結果如圖4所示。

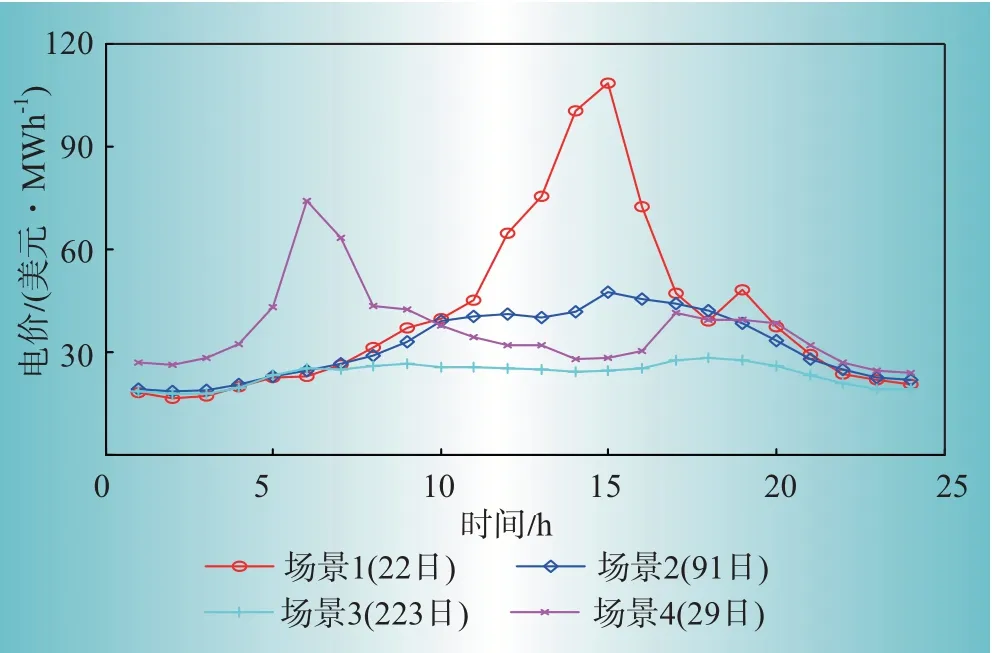
圖4 2016年實時電價數據聚類結果Fig.4 Clustering results of real?time electricity price data in 2016

圖4的圖注中各場景后括號內日數表示該電價聚類場景的相似日數量。可以看出，不同場景之間的電價曲線波動差異非常明顯，因此，考慮到市場電價的不確定性，對于聚集商的投資規劃是必要的。圖4中，場景1和場景4的相似日數量在全年中雖然僅占22 日和29 日，但其一天內的電價峰值和波動幅值均較大，是典型的需求響應投標日。

事實上，不同年份的電價數據聚類結果之間同樣有明顯差異，因此考慮較長時間尺度（規劃前4年）的歷史電價信息能夠增加算例中聚集商規劃結果的可信程度。

3.2 風險偏好對規劃方案、利潤和風險的影響

為研究聚集商在不同風險偏好下對規劃方案、利潤和風險帶來的影響，設定μ區間為［0.02，0.9］，求解所得需求響應資源規劃方案如表3所示。

表3 不同風險偏好下的需求響應資源規劃結果Table 3 Results of demand response resources’planning under different risk preferences

從表3 的規劃結果來看，考慮用戶行為不確定性時，投資者的需求響應資源規劃結果明顯地受到風險偏好μ的影響。當μ為0.02，即聚集商對風險偏好很低時，聚集商的規劃方案是僅采用442 組用戶側TL2，未配置其他類型可調負荷和ES，此時由于TL2 的響應價格低而不確定性高，聚集商在獲得較高收益的同時也面臨很高的潛在平均超額損失，為激進型規劃方案。然而，隨著風險偏好系數的不斷增大，聚集商對風險的厭惡程度增強，其規劃偏好逐漸向高響應價格和低不確定性的IL 及ES 傾斜，投資方案趨于保守化。進一步地，當μ達到0.9時，聚集商配置了35組ES同時完全放棄了TL2的規劃，在該投資方案下，聚集商的平均超額損失極低，僅為30.5 美元，但同時聚集商獲取的利潤期望較低，機會成本上升，規劃方案非常保守。

事實上，若不考慮用戶行為不確定性，聚集商的規劃方案將不受μ的影響，而是優先規劃低響應成本的可調負荷，從而獲得更高的期望利潤，但這種規劃方案顯然難以應對實際風險，可信度較低。

根據表3 的聚集商風險偏好、年利潤、VaR 和CVaR值，繪制三維有效前沿，如圖5所示。

由圖5可知，CVaR前沿曲線的正上方區域為所有規劃組合的可行域，而聚集商的最優規劃組合在CVaR有效前沿上。當聚集商利潤增大時，圖示2條前沿曲線均呈現風險上升趨勢，這揭示了聚集商在規劃中“高風險帶來高收益”的投資規律。同時，當風險偏好系數逐漸減小時，CVaR 前沿的風險總體上升曲率逐漸增大，這意味著增加同樣的利潤值時，風險水平增加的幅度不斷增大，該規律值得激進型投資商的注意。

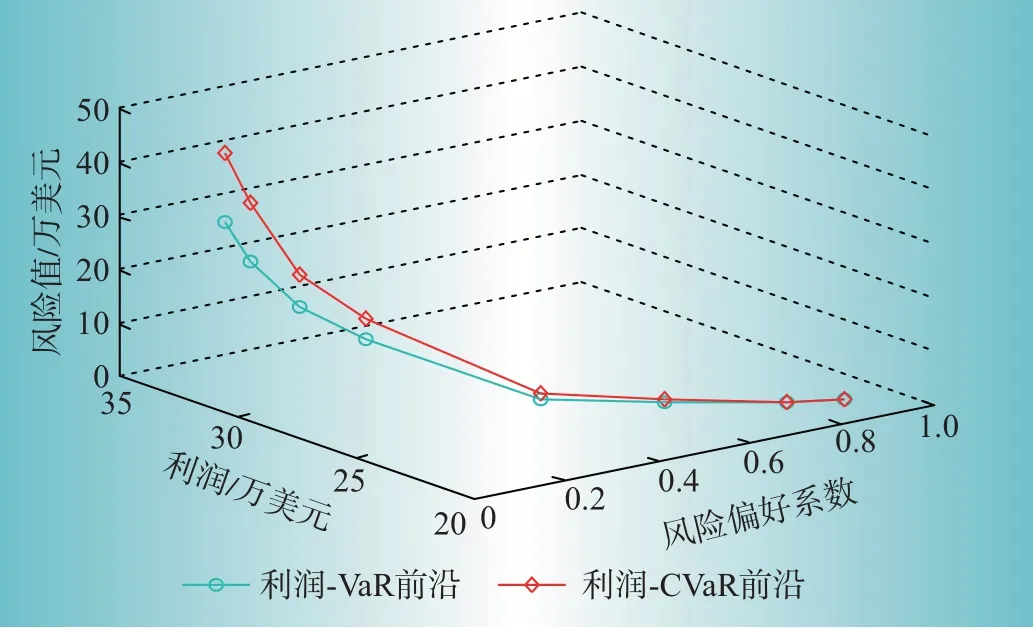
圖5 聚集商VaR和CVaR的有效前沿曲線Fig.5 VaR and CVaR effective frontier curves of the load aggregator

3.3 聚集商日響應場景分析

當聚集商確定規劃方案后，可在相對短的時間尺度上進一步分析其日響應計劃。選取2016 年電價聚類曲線場景1，以μ=0.8 得到的規劃結果為例進行分析，描繪聚集商日響應計劃如圖6所示。

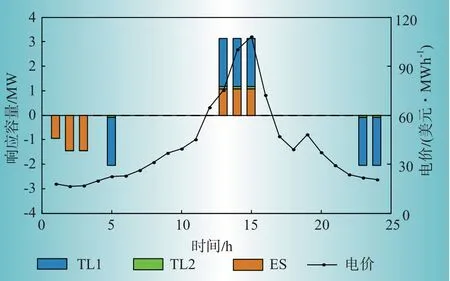
圖6 聚集商日響應計劃Fig.6 Daily response plan of the load aggregator

由圖6可見，該場景下，聚集商選擇在高電價時段（13:00—16:00）投標，安排用戶側TL1、TL2和ES參與響應，總響應容量達到3.12 MW。同時，該場景中響應價格低但不確定性高的TL2 的響應容量僅為0.1 MW，這是由于聚集商在μ=0.8的保守規劃策略下，為減少風險，盡可能避免安排TL2參與響應。此外，ES的充電計劃安排在電價最低時段（1:00—4:00），而2 類可轉移負荷則分別轉移到用戶意愿時段范圍內（5:00—6:00、23:00—1:00）。

4 結束語

本文首先基于聚集商的市場化運營框架分析其面臨的雙側不確定性，即電價不確定性和用戶響應行為不確定性。然后，引入CVaR 理論建立聚集商需求響應資源規劃模型。所建模型采用歷史模擬法處理電價不確定性，采用隨機模擬法處理用戶行為不確定性，同時采用k 均值聚類算法對歷史電價場景進行縮減，有效地提高了模型仿真速度。算例分析表明:① 考慮雙側不確定性能增加算例仿真的可信度，在聚集商的規劃研究中具有顯著的必要性；② 引入CVaR理論能有效地度量聚集商的投資風險，為投資者提供直觀的風險評價參考；③ 投資風險總是伴隨利潤的增長而上升，聚集商應當意識到儲能設備在平抑風險中的作用，并結合自身的實際風險偏好進行需求響應資源規劃。D