頻率估計的ANF誤差函數分析及在科氏流量計中的應用

李 明，涂亞慶，萬 平，肖 瑋，陳 鵬

（陸軍勤務學院，重慶 401311）

0 引 言

自適應陷波器（ANF）頻率估計方法在衛星導航定位、工業控制與儀表、醫學工程等物聯網技術中應用廣泛[1-4]。相比基于FFT離散頻譜校正的傳統頻率估計方法[5-6]，ANF頻率估計方法計算過程更簡便，具備良好的抗噪性能，更為重要的是無頻譜泄漏。ANF通過采用自適應方式調整濾波器參數，基于時域遞推估計方法對輸入信號的頻率進行實時估計，這不僅適用于估計時不變的信號頻率，且對時變信號，即頻率時刻發生變化的信號也適用。此外，它還具備較好的估計性能，有效克服了傳統基于FFT頻率估計方法的局限性。ANF具備較多優點，但在具體應用過程中也存在一些缺點，如針對頻率靠近頻譜兩端的正弦信號，即信號頻率接近于0或π時，其頻率估計精度會出現一定下降，且收斂速度受參數影響較大，頻率估計易出現不穩定的情況[7]。

究其原因，主要是ANF自身所采用的誤差函數過于平緩，ANF根據誤差函數梯度值搜尋全局極值點較緩慢，從而導致ANF收斂速度慢、自身不穩定的情況出現。為解決現有ANF頻率估計方法存在的收斂速度慢、精度低、穩定性差等不足，文中通過分析多種誤差函數的性能，提出一種新的誤差函數。該函數改善了ANF在整個頻率范圍內的迭代收斂曲面，提高了ANF頻率估計精度，加快了ANF收斂速度，提升了ANF穩定性。同基于原誤差函數的ANF頻率估計方法進行比較，驗證了本文所提方法的有效性。

1 誤差函數分析

正弦信號如式（1）所示：

式中：A為信號幅值；ω0為信號頻率；θ為信號相位，服從[0, 2π）的均勻分布；v0(k)是服從N(0,σ2)的加性高斯白噪聲；N為采樣信號長度。

ANF傳遞函數如式（2）所示：

式中：0＜ρ＜1，用以控制ANF的陷波寬度；ANF參數a=-2cosω，ω為陷波器頻率，在ANF頻率估計過程中ω→ω0。ANF的FIR和IIR結構分別為N(z,a)和H(z,a)，e1(k)和e2(k)分別為x(k)通過N(z,a)和H(z,a)的信號，如式（3）所示：

ANF通過自適應調整參數a獲得正弦信號頻率值，使式（4）～式（6）的誤差函數最小化[8-10]：

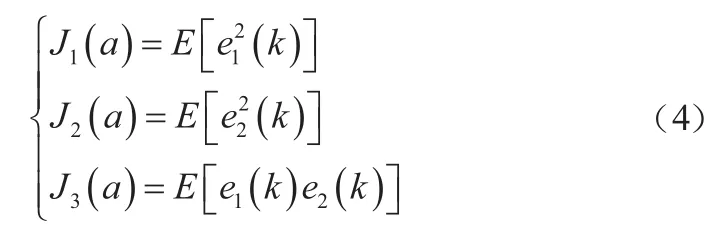
式中，E[·]表示求取期望。實際計算時按式（5）所示計算：

由于輸入信號為正弦信號，故式（2）中N(z,a)和H(z,a)在輸入信號頻率z=ejω0處的幅值為：

相角為：

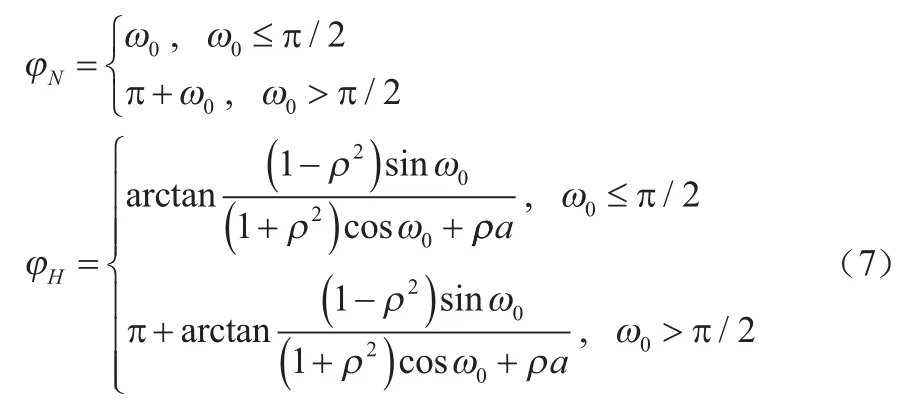
結合式（3）、式（6）、式（7），可得：

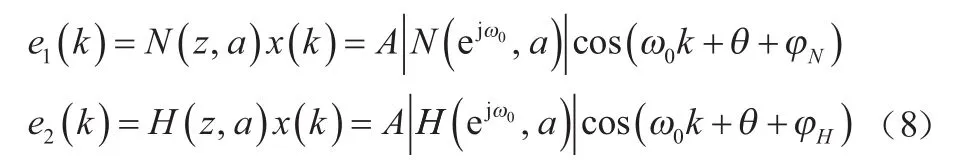
將式（6）～式（8）代入式（4），可得式（9），式（9）分別對a求導，可得式（10）。

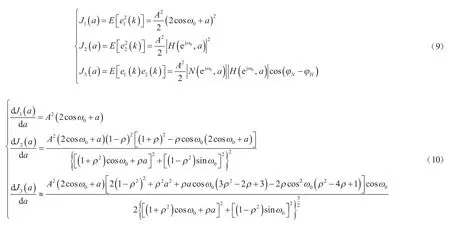
由式（10）可獲得誤差函數導數的理論計算值。在實際計算中，可采用式（11）進行計算：

由式（5）可得：

式中[10]：A=1，θ=π/6，ρ=0.95，N=200。按式（12）計算不同誤差函數的導數值，如圖1所示，導數為0點處為最優頻率估計解。

圖1 A=1，θ=π/6，ρ=0.95，N=200時，不同誤差函數的導數值

由圖1可知，當信號頻率ω0=π/3時，文獻[8]所提誤差函數受噪聲影響較大，低信噪比條件下頻率估計值發生偏轉，但具備良好的梯度值，收斂速度可得到保證。當信號頻率靠近頻譜兩端時，其誤差函數性能出現較大幅度下降。

文獻[9]所提誤差函數受噪聲影響較小，且靠近頻譜兩端信號，其函數性能未出現明顯變化，但其整體梯度值較小，導致算法收斂速度過慢。

文獻[10]所提誤差函數，當頻率ω0=π/3時，其極值點不唯一，將限制其初始頻率的選擇。針對頻譜兩端信號，其導數為0點不存在，導致頻率估計精度下降，無法獲得滿意結果。

根據上述三種誤差函數的優缺點，本文提出一種新誤差函數，使其在頻率范圍內具備較好的梯度值，且受噪聲影響較小。針對頻譜兩端信號，其誤差函數能保持優良性能。本文將ANF的FIR結構和IIR結構輸出信號的和的平方作為新誤差函數，如式（13）所示：

在實際計算中可按式（14）進行計算：

其導函數為：

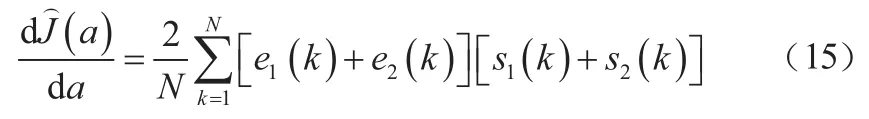
結合式（9）可知新誤差函數的理論計算值為：

保持參數不變，本文所提新誤差函數的導函數如圖2所示。不論待估頻率為ω0=π/3還是ω0=π/20，誤差函數在導數值為0處獲得極值點，且極值點唯一。當初始頻率值與最優頻率解相距較遠時，其誤差函數的導數值較大，當誤差函數保持較大梯度值時，可加快其收斂速度。

圖2 參數保持不變，SNR=5 dB時誤差函數的導數值

2 應用分析

2.1 計算分析

根據式（12）和式（15），不同誤差函數所得頻率估計方法如下所示：

為了獲得頻率估計收斂速度與精度的比較結果，信號及ANF參數設定為：A=1，θ=π/6，ρ=0.95，信噪比為5 dB。考慮到對稱性，故只針對頻率接近0時的信號，信號頻率ω0從π/20變為 0.7π，從 0.01π變為 0.2π，即a=-2cosω0從 -1.975 4變為 1.175 6，從 -1.999 0 變為 -1.618 0。步長μ=2×10-4，ANF參數a初值設為0。頻率變化條件下不同方法的頻率估計結果如圖3所示。

圖3 頻率變化條件下不同方法的頻率估計結果

由圖3可知，文獻[8]誤差函數由于受噪聲影響較大，其方法在低信噪比條件下喪失了頻率估計能力；文獻[9]誤差函數由于梯度值過于平緩，導致收斂速度過慢，無法及時得出令人滿意的頻率估計結果；文獻[10]誤差函數雖具備較為適中的收斂速度和精度，但當信號頻率發生變化時，其頻率估計精度存在一定的不穩定性。本文所提新誤差函數具備良好的梯度，且自身性能滿足不同條件下的頻率估計要求，可得出較好的收斂速度和頻率估計精度。

2.2 實驗分析

為驗證所提新誤差函數的性能，本文針對項目組自行研制的科里奧利質量流量計（Coriolis Mass Flowmeter，CMF）實驗平臺頻率估計問題進行實驗分析。該CMF型號為進口羅斯蒙特CMF-FS200型。科氏流量計實驗平臺如圖4所示。實驗分析中流量計示值為0～105.2 kg/min，CMF頻率值約為 198 Hz，采樣頻率為 20 000 Hz，即ω0=0.062 2，a0=-1.996 1，參數設置μ=2×10-4，ρ=0.95，a(0)=0。流量處于0～105.2 kg/min范圍時，不同方法的頻率估計結果如圖5所示。

圖4 科氏流量計實驗平臺

圖5 流量處于0～105.2 kg/min范圍時，不同方法的頻率估計結果

由圖5可知，本文所提新誤差函數頻率估計方法的性能同實驗分析結果基本一致，具備收斂速度快、頻率估計精度高、穩定性好等特點。

3 結 語

本文在分析不同誤差函數及其導數性能的基礎上，提出的新誤差函數具備良好的梯度值，可有效提升基于該新誤差函數ANF頻率估計方法的收斂性能及頻率估計精度。實驗分析表明，該新誤差函數適用范圍較廣，可滿足頻率變化要求，尤其針對頻譜接近0或π條件下的頻率估計問題，可有效增強ANF頻率估計方法的穩定性，應用前景較好。