指標權重算法對Fisher最優分割在水庫汛期分期中的影響研究

虞 慧，劉星根，吳曉彬，王永文，王 姣，彭圣軍

(1．江西省水利科學研究院，南昌 330029；2．江西省水工程安全工程技術中心，南昌 330029；3．中國科學院南京地理與湖泊研究所，南京 210008；4．中國科學院大學，北京 100049；5．南昌工程學院，南昌 330099)

0 引 言

水庫是人類利用水資源的重要方式，具有灌溉、防洪、供水、發電、航運等功能。截至2019年8月底，江西省已注冊登記水庫大壩共10 672 座，其中大型30 座，中型258 座，小(Ⅰ)型1 468 座，小(Ⅱ)型8 921 座。由于流域降雨和徑流的季節性變化，流域的水資源供需矛盾越來越顯著，水庫管理面臨著越來越突出的防洪和興利的矛盾。水庫汛期分期針對兩者的矛盾，以期在不增加防洪風險的前提下[1]，緩解旱澇急轉的風險，最大化地利用汛后期的洪水資源。汛期分期的方法從定性分析、定量計算方法，逐步發展至精細化定量的新方法上。高波等[2]和談亞琦[3]通過引入系統聚類方法，在分析水庫多個影響因子的基礎上，構建模糊相似矩陣進行水庫汛期分期；劉攀等[4,5]通過采用基于超定量取樣的概率變點分期模型的變點分析方法對隔河巖水庫進行分期分析；陳守煜等[6,7]和莫崇勛等[8]采用統計多指標下隸屬于汛期的隸屬度的模糊集分析法進行分析；謝飛和王文圣[9]采用基于聯系度的概念進行集對分析法分析。劉克琳等[10]采用對有序樣本進行分類的Fisher最優分割法進行分割，取得了較好的效果。每種方法均有其固有的特性和適用性，系統聚類法具有較強的理論意義，但無法給出最優的結果；變點分析法需要進行數學假定，具有一定的主觀性；模糊集分析法采用單個指標進行分析，具有一定的局限性；集對分析在指標閾值確定上存在主觀性。

Fisher最優分割在汛期分期研究中應用廣泛[10-12]，如汾河張家莊水庫、海河密云水庫、渭河石頭河水庫、黃河太平水庫、珠江澄碧河水庫等的研究結果均表明該方法的分期結果能較好地反映水庫流域的氣象水文背景和暴雨徑流特征，為水庫優化運行管理、提高水庫運行效益提供科學依據[10,13-16]。Fisher最優分割法考慮了降雨、徑流等多指標的綜合作用和時序性，確定最優分類數及時段[15]。許多研究者提出了Fisher最優分割中指標權重的確定方法，以期減少指標權重的主觀性及其對分割結果的影響[13-16]，比如相關系數法、主成分分析法、模糊層次分析法等。然而，不同方法確定的指標權重可能存在一定差異，這種差異對Fisher最優分割結果的影響尚未充分探討。為進一步理清指標權重對Fisher最優分割結果的影響，本文以七一水庫為例，比較分析了主成分分析法、變異系數法、熵權法等三種方法在確定指標權重的差異，并在此基礎之上分析了指標權重差異對Fisher最優分割結果的影響，以期為今后汛期分期研究和實踐提供參考。

1 方法理論

1.1 Fisher最優分割

1.1.1 基本原理

Fisher最優分割是針對有序樣品進行最優化分段的一種數學聚類方法[17]。它根據樣本段內差異最小、樣本分段之間差異最大的原則劃分樣本最優分段，采用離差平方和量化樣本內部、樣本分段之間的差異[10,13]。

1.1.2 計算步驟

Fisher最優分割在水庫汛期分期中的一般步驟為[10]：

(1)選取指標。對水庫所處流域的水文、氣象資料進行分析，根據需求綜合分析并篩選出能反映汛期分期的各種指標參數。

(2)構建初始分類樣本。選取汛期分期的指標值Xij(i=1 ～n,j=1 ～m)，其中i代表樣本，j代表指標，構建樣本與指標之間的關系矩陣X，對指標數據進行最大最小值標準化得到標準化矩陣X′：

(1)

按照各指標對樣本分類的重要程度賦予權重系數w1,w2,…,wn，加權平均后將多指標值矩陣轉化為初始分類樣本Y:

(2)

(3)

(4)

式中：yr為樣本值。

(4)確定目標函數。通過將n個有序樣本分割為k段，從而定義出目標函數，{yj1,yj1+1,…,yj2-1}，{yj2,yj2+1,…,yj3-1}，…，{yjk,yjk+1,…,yjk+1-1}，其中j1，j2，…，jk為k個分點，最優分割的實質就是尋找某一組分點，使得所有分類的直徑總和最小，即：

(5)

(5)求解最優分割。有序樣本的最優k類分割一定是在其某一個截尾子段最優k-1類分割之后再添加一類形成的。使用以下遞推公式求解最優分割。

B(n,2)=min{D(1,j-1)+D(j,n)}

(6)

B(n,k)=min{B(j-1,k-1)+D(j,n)}

(7)

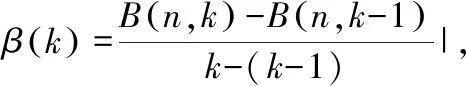
(7)最優分類結果的F檢驗。對分類結果進行F檢驗，構建F統計量[18]：

(8)

1.2 權重因子的計算

根據上述計算步驟，增加權重因子計算部分，詳見圖1。

Fisher最優分割根據各指標對樣本分類的重要性賦予權重系數w1,w2,…,wn，權重系數的大小可能影響最優分割結果。基于前人研究結果[13-16,19]，本文選擇主成分分析法、熵權法和變異系數法確定權重系數，比較3種方法對Fisher最優分割結果的影響程度。

1.2.1 主成分分析法

主成分分析法(Principal Component Analysis, PCA)由Karl和Pearson提出，利用變量的線性變換，尋找一組新的不相關的變量，原則是保持變量的總方差不變，根據變量的方差大小確定主成分的順序，從而減少變量的冗余信息，最大程度的挖掘變量包含的信息[19]。根據主成分的貢獻率以及與各指標的相關程度確定綜合得分模型，其中綜合得分模型的系數反映各指標變量在主成分中的綜合重要度，據此可以確定指標變量的權重[16,19]。主成分分析法確定權重的具體步驟較為常見[19]，在此不再詳述。

1.2.2 熵權法

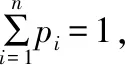
(9)

由信息熵與指標權重的關系定義指標的熵權：

(10)

1.2.3 變異系數法

變異系數法認為當某一指標值的變異程度越大，反映系統特征的差異越大，指標的區別程度越好，應該賦予較大的權重，反之亦然[23]，例如李俊應用變異系數法和模糊集理論確定黃河流域吳城水庫的汛期分期[24]。設x的取值為X={x1,x2,…,xi-1,xi}，則該指標的變異系數為：

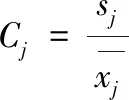
(11)

指標權重為：

(12)

2 實 例

2.1 研究區概況和數據

江西省七一水庫位于信江支流金沙溪中游，壩址以上控制流域面積324 km2，水庫的總庫容22 800 萬m3，正常蓄水位160.40 m(黃海高程，下同)，是一座以灌溉為主，兼有防洪、發電、供水等綜合效益的大(Ⅱ)型水庫。七一水庫現行防洪運行方式為：主汛期為4月1日-6月30日，主汛期汛限水位為159.00 m；后汛期為7月1日-9月30日，后汛期汛限水位為160.00 m。

本次所使用的基礎數據為七一水庫、土城、童家坊3個雨量站的逐日降雨資料，七一水庫逐日入庫流量資料。分期使用降雨資料為七一水庫站和土城站的逐日降雨的算術平均值，1993年后的土城站的資料，移用童家坊的降雨資料進行延長，因童家坊和土城的同時期的(1970-1992年)的年降雨相關性達0.96。根據水庫所處流域的氣象水文背景和相關文獻調研[4-8]，本文汛期分期指標采用以下6個指標，包括旬最大日流量，旬平均日流量，旬暴雨日數，旬最大日雨量，旬最大3日雨量和旬雨量和。

2.2 分期計算

2.2.1 權重計算結果

3種方法計算的指標權重如表1。權重差異最大的指標為旬暴雨日數，變異系數法和熵權法確定的旬暴雨日數權重較大(分別為0.34，0.43)，而主成分分析法對應的該指標權重小于0.2。暴雨事件的隨機性較大，旬暴雨日數的變化范圍為0～4 d。在全部指標的變異程度上，旬暴雨日數的變異系數最大。因此前兩種方法確定的旬暴雨日數指標權重為最大值，反映該指標的不確定性程度最大。除旬暴雨日數，變異系數法和熵權法確定的旬最大日流量等5個指標的權重基本一致。主成分分析法確定的6個指標權重中僅有2個指標(旬最大日流量、旬平均日流量)的權重與前兩種方法的結果一致，其他指標與前兩種方法的結果差異較大。

就不同指標的差異而言，旬暴雨日數的變異性最大(變異系數為3.24)，其次為流量指標(旬最大日流量、旬平均日流量)，變異系數為1.50～1.63，而雨量指標(旬最大日雨量、旬最大3日雨量、旬雨量)的變異性最小，變異系數在1.03～1.13。變異性越大反映指標的不確定性程度越強，指標提供的系統的信息越多。因此暴雨日數對汛期分期可能存在較大影響，其次為流量相關的指標，而雨量相關的指標對汛期分期的影響可能較小。同時，由于旬最大日雨量和旬最大3日雨量兩個指標的變異系數非常接近，且兩者存在較好的相關性，意味著兩個指標存在一定同一性，今后的汛期分期中則可以適當減少雨量指標的數量。

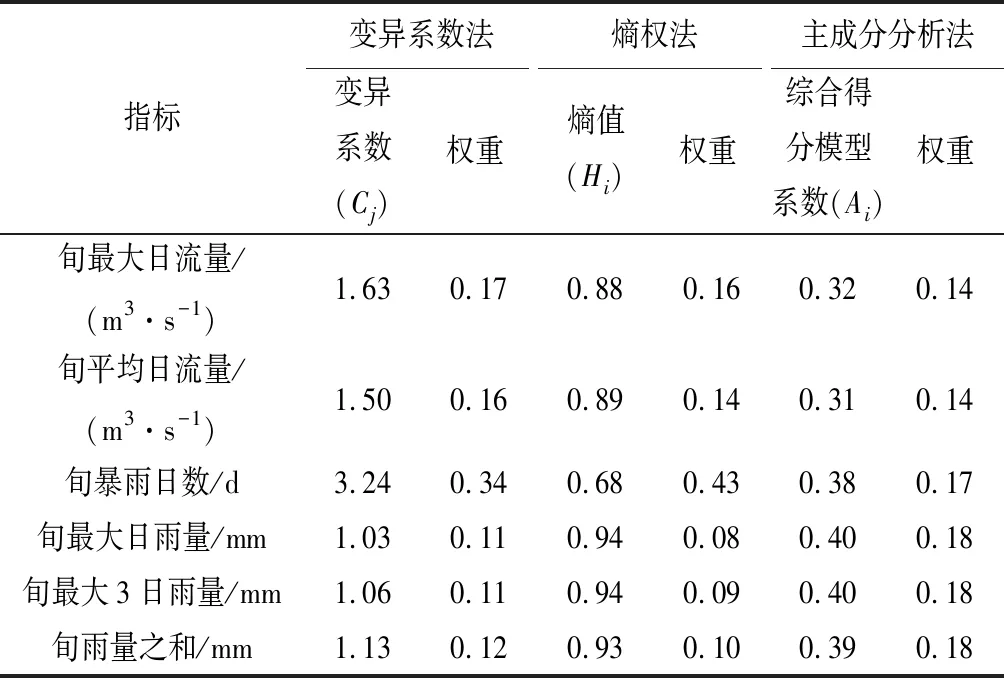
表1 3種方法計算成果Tab.1 Calculation results of three methods

2.2.2 Fisher最優分割結果

各方法計算所得權重系數與各指標值代入公式(2)得到初始樣本分類向量(圖2)，應用最優分割遞推算法[公式(5)～(7)]可得不同分類數對應的最小目標函數值和分割位置(圖3和表2，表2以變異系數法權重的計算結果為例，其他方法計算結果省略)。由計算結果可知，k=3時曲線存在明顯拐點，相應的分期為{1，10}，{11，12}，{13，21}，即3月上旬-6月上旬為前汛期，6月中旬-6月下旬為主汛期，7月上旬-9月下旬為后汛期。

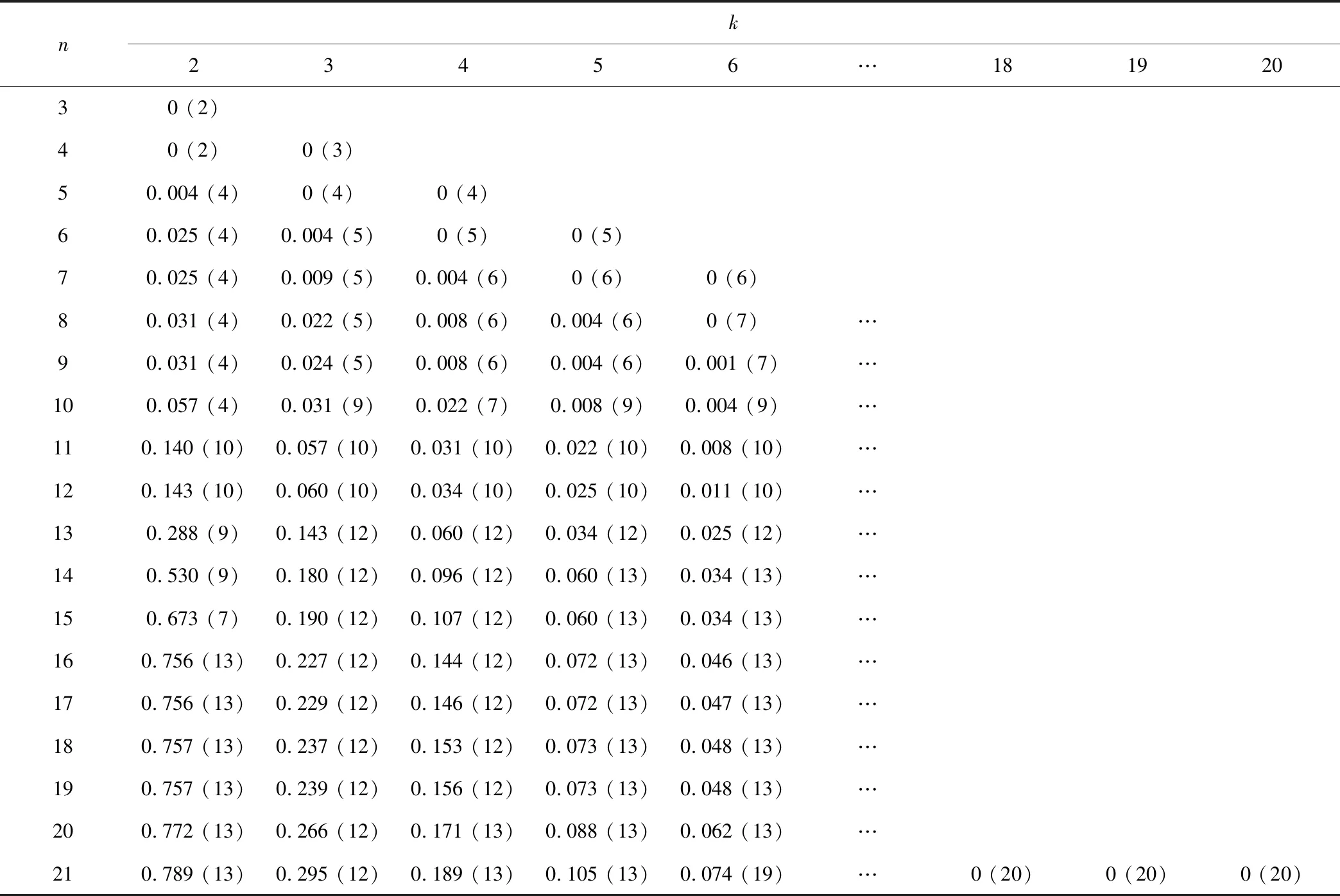
表2 目標函數計算結果(變異系數法)Tab2. Calculation result of objective function (variation coefficient method)

為進一步精細化分析汛期時段區間，同時根據水庫實際調度的需求進行分析，當k=3時前汛期長達3個月，不利于水庫動態汛限水位調控，而且在后汛期中7月上旬與7月下旬-9月下旬的樣本值存在明顯的差異(圖2)，體現其過渡性特征，另外，4月中旬-5月的樣本值與3月也存在一定的差異，反映主汛期與前汛期、后汛期之間的過渡性，綜合以上考慮，水庫汛期可劃分為5期，根據Fisher最優分割法對k=5進行分期，其相應分期為{1，4}，{5，10}，{11，12}，{13}，{14，21}，即3月上旬-4月上旬為前汛期，4月中旬-6月上旬為前汛過渡期，6月中旬-6月下旬為主汛期，7月上旬為后汛過渡期，7月中旬-9月下旬為后汛期。從分期結果上看，七一水庫汛期分5期是在3期的結果上進一步的細化，整體結果隸屬于3期的分期結果。

進一步對分類數為5類時的分期結果進行F檢驗發現，自由度分別為4和16，F=48>Fα=4.07，即在0.01的顯著性水平上分期結果之間存在顯著差異。應用熵權法和主成分分析法權重的Fisher最優分割結果與變異系數法權重的Fisher最優分割結果一致，此處不再贅述。

2.3 分期結果比較

2.3.1 成因分析

金沙溪流域位于贛東北暴雨中心邊緣，以亞熱帶鋒面氣旋雨為主，常出現在5-7月份。因孟加拉灣和南海暖濕氣流與北方冷空氣團相遇時切交線的南北徘徊，容易形成暴雨過程。暴雨移動方向大多由西至東，或西北向東南移動，有時出現靜止鋒，形成暴雨中心穩定少動現象[25]。實測資料表明，每年暴雨次數約為3～7次，雨量占全年的15%～25%。一次暴雨持續時間大多為1～2 d，持續時間在3～4 d以上的很少。7-9月則以不穩定的熱氣流上升形成的雷陣雨為主，雨區較小，歷時短，強度較大，但日雨量不大。期間偶有西太平洋入侵大陸的臺風影響，形成歷時較短、風強、雨量較大的降雨過程。10月-次年2月，主要受西伯利亞和蒙古干冷氣流影響，一般降雨量較小，僅占全年的32%[25]。

金沙溪為雨源性補給河流，流域調蓄能力較差。徑流、水位隨降雨情況而變化，年內分配不均勻。根據1960-2017年七一水庫站統計資料，10月-次年1月為枯水期，來水量占全年的16%。3-6月為豐水期(汛期)，來水量占全年的57%，其余各月為平水期。洪水出現季節多在5-6月。因此，從流域所處的水文氣候背景來看，水庫的主汛期宜為5-6月，汛前期可能在3-4月，而汛后期宜為7-9月，這一劃分與本文的汛期分期結果基本一致。

2.3.2 數理統計

圖4是各旬暴雨日數、雨量、最大日流量和入庫水量的統計特征。總體而言，不同期間的水文氣象指標存在較大差異。主汛期(6月中旬-下旬)的各項指標均為最大值，因此6月中旬-下旬劃分為主汛期符合水庫流域的暴雨徑流特征。汛后過渡期(7月上旬)的各項指標位于主汛期和汛后期的過渡狀態。盡管汛前過渡期(4月中旬-6月上旬)與汛前期(3月上旬-4月上旬)的旬雨量和入庫水量差異較小，但汛前過渡期的暴雨日數和最大日流量與汛前期存在較大差異，說明汛前過渡期與汛前期的總降雨和徑流量差異不大，但汛前過渡期存在較多的暴雨事件，形成的最大日流量明顯大于汛前期，反映其水文氣象特征的過渡特性，因此4月中旬-6月上旬劃分為汛前的過渡期也較為合理。汛前(3月上旬-4月上旬)和汛后期(7月中旬-9月下旬)的各項水文氣象指標均為最小值，因此各劃分為單獨的一期。因此，數理統計分析結果與本文使用Fisher最優分割結果是一致的，反映本文分期結果的合理性。

2.3.3 系統聚類

本文采用系統聚類法[2,3]對七一水庫的汛期進行聚類分析，基于旬最大日流量、旬平均日流量、旬暴雨日數、旬最大日雨量、旬最大3日雨量和旬雨量和等6個指標的層次聚類結果如圖5。圖示可知，研究樣本可劃分為4類，分別為{11，12}，{5，7～10，13}，{1～4，6}，{14～21}，對應時期為{6月中下旬}、{4月中旬，5月-6月上旬，7月上旬}、{3月-4月上旬，4月下旬}、{7月中旬-9月}。基于系統聚類的結果與基于Fisher最優分割的分期結果基本上是一致的，其中第一類{6月中下旬}為主汛期，第二類{4月中旬，5月-6月上旬，7月上旬}以主汛期為界，劃分為汛前過渡期{4月中旬-6月上旬}和汛后過渡期{7月上旬}，第三類{3月-4月上旬，4月下旬}中的{3月-4月上旬}為汛前期，{4月下旬}劃分至汛前過渡期，第四類{7月中旬-9月}為汛后期。

3 結論與建議

(1)通過對七一水庫汛期分期計算及分析，認為主成分分析法、熵權法和變異系數法確定指標的權重均適用于Fisher最優分割在水庫汛期分期。計算結果表明，3種方法計算的權重存在一定的差異，但這種差異對最終的分期結果的影響較小。

(2)就3種方法確定指標權重而言，變異系數法和熵權法更適用于指標權重的確定。變異系數法和熵權法量化了指標的不確定性程度，兩者計算的指標權重較為一致，較好的區分出暴雨日數、流量、雨量等不同指標的差異；主成分分析方法計算的各指標之間的權重差異較小，難以揭示不同水文氣象指標的差異性。

(3)不同算法所得的指標權重結果應用于七一水庫汛期分期計算，其采用Fisher最優分割法的結果與數理統計、系統聚類等方法的分析結果一致，可為水庫汛期優化調度提供參考。

(4)通過對確定指標權重的3種方法計算表明，今后汛期分期工作中可以對權重算法所得的指標變異系數進行分析，從而為后期優選適宜于該流域汛期分期的關鍵指標提供參考。

□