階估計(jì)法在判斷瑕積分審斂法中的應(yīng)用
張祖敘,孫榮璞,尹凱倩
(山東科技大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266590)
通過(guò)對(duì)微積分的學(xué)習(xí),可以利用比較原則、柯西判別法、狄利克雷判別法和阿貝爾判別法等[1]來(lái)判斷瑕積分的斂散性。從判別法的不同角度對(duì)階估計(jì)法進(jìn)行研究,得到審斂性的定理。已有研究者對(duì)判別法進(jìn)行過(guò)細(xì)致而全面的研究,如齊紫微[2]等學(xué)者給出的基于階估計(jì)法的無(wú)窮廣義積分審斂性定理。我們通過(guò)階估計(jì)法推導(dǎo)了判斷瑕積分?jǐn)可⑿缘呐袆e法,并通過(guò)比較判別法進(jìn)行證明并附以實(shí)例,驗(yàn)證了審斂法的有效性和實(shí)用性。
1 基于階估計(jì)法的瑕積分審斂性判別法
定理1.設(shè)f(x)是定義在區(qū)間(a,b]上的非負(fù)可積函數(shù),且滿足:
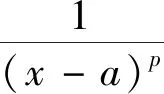
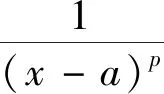
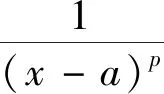

易見(jiàn)瑕積分收斂,由比較判別法,瑕積分同樣收斂。
②當(dāng)p≥1時(shí),經(jīng)過(guò)計(jì)算可知:

小結(jié):在微積分學(xué)中只討論了分式的奇點(diǎn)為0的判別法,而定理1給出了分式的起點(diǎn)不為0的一般情況。
定理2.設(shè)f(x),g(x)是定義在區(qū)間(a,b]上的非負(fù)函數(shù),則:



證明:



小結(jié):與定理1提出的思路相一致,根據(jù)由特殊到一般的數(shù)學(xué)思想,對(duì)微積分學(xué)中的原有積分進(jìn)行了簡(jiǎn)單推廣。
定理3.設(shè)f(x)是定義在區(qū)間[a,b)上的非負(fù)可積函數(shù),則:


證明:

①0 ②p≥1時(shí): 結(jié)合①②兩點(diǎn),得到了定理3的證明。 小結(jié):定理3對(duì)應(yīng)于微積分學(xué)中廣義積分的階判別法,將廣義積分調(diào)整為積分區(qū)間為半閉半開(kāi)區(qū)間的瑕積分。 定理4.設(shè)f(x)是定義在區(qū)間(a,b)上的非負(fù)可積函數(shù)(a和b都是瑕點(diǎn)),且對(duì)于?p∈(0,1)及c∈(a,b),滿足: 證明: 小結(jié):與定理3相比較,發(fā)現(xiàn)積分區(qū)間兩端均為瑕點(diǎn)。在證明該定理的過(guò)程中,對(duì)給定的積分區(qū)間進(jìn)行分段,從而歸結(jié)為定理3的結(jié)果。 又因?yàn)閠anx~x(x→0),ex-1~x(x→0),所以有: 解: 根據(jù)瑕積分階估計(jì)法,推廣了微積分學(xué)中分式奇點(diǎn)為0的一般情況,并提高了階估計(jì)法的適用范圍,通過(guò)實(shí)例的引入,驗(yàn)證了審斂法的有效性和實(shí)用性。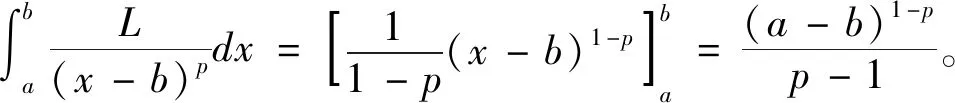

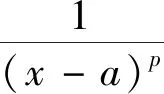


2 定理應(yīng)用





3 結(jié)語(yǔ)

