洪水預報智能模型在中國半干旱半濕潤區的應用對比

張 珂，牛杰帆，李 曦，晁麗君

(1.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210098；2.河海大學水文水資源學院，江蘇 南京 210098； 3.長江保護與綠色發展研究院，江蘇 南京 210098；4.中國氣象局-河海大學水文氣象研究聯合實驗室，江蘇 南京 210098)

近年來，受氣候變化和人類活動的影響，極端天氣頻發，山洪、泥石流、城市內澇等自然災害不斷發生。尤其位于山區的中小流域，由于洪水突發性強、匯流快、預見期短，災害發生迅猛，給防汛工作帶來了嚴峻考驗[1-3]。洪水預報主要依賴模型模擬，目前洪水預報模型可分為兩大類：基于物理過程的傳統水文模型[4-6]和數據驅動的人工智能模型[7-8]。傳統水文模型具有明確和相對固定的物理關系基礎[9]，在實際應用過程中一般對下墊面變化導致的物理關系變化考慮不足。智能模型在模擬中依靠人工智能技術，通過不斷獲取的數據進行自我學習，不需要流域水文的先驗知識，能夠從多角度捕捉水文數據中的復雜非線性關系，具有強大的仿真能力，在水文預報中應用越來越廣泛[10-15]。

國內外學者在利用人工智能模型進行水文預報方面做過許多研究。霍文博等[16]使用支持向量機模型與新安江模型進行實時洪水預報比較研究，發現支持向量機模型在短預見期實時預報中更具優勢，在率定期和測試期中均具有較高精度；徐源浩等[17]使用長短時記憶神經網絡建立不同預見期的暴雨洪水模型，對黃河中游洪水過程進行模擬，研究發現6 h預見期內模型預報精度較高；Yaseen等[18]提出了一種改進的極限學習機模型應用于熱帶地區的流量預測中，發現改進后的模型各項評價指標得到了顯著提高，具有廣泛的應用前景；Tikhamarine等[19]將灰狼優化算法與智能模型結合建立了更加高效的水文預報系統，在月徑流預測中取得了較好的效果；Zhou等[20]提出將基于遞歸的自適應模糊神經網絡模型運用于水文預測，相比于傳統自適應神經網絡，改進后的模型能夠適應非平穩的降雨徑流過程，具有更高的模型效率與可靠性。

目前國內外學者針對智能模型的水文預報應用研究較多，并取得了很好的成果，但研究主要集中于單一智能模型的改進和多種智能模型的集成優化，對于多種智能模型實時洪水預測的對比研究較少。本文使用決策樹、多層感知器、隨機森林和支持向量機4種智能模型對陜西省的3個半干旱半濕潤典型流域進行逐時洪水預報，比較4種模型在半干旱和半濕潤區的預報結果，探究人工智能模型在洪水預報中的適用性。

1 研究區概況

選取陜西省的志丹流域、板橋流域、馬渡王流域3個流域作為研究區域(圖1)，其中志丹流域為半干旱流域，板橋流域和馬渡王流域為半濕潤流域。志丹流域集水面積為777 km2，區域氣候隸屬于中溫帶半干旱氣候，多年平均降水量為510 mm；受地形地貌影響，志丹流域河網密度較大，洪水漲落快，歷時較短。馬渡王流域面積為1 604 km2，屬暖溫帶半濕潤大陸性季風氣候，多年平均降水量 631 mm，流域山區地勢陡峭，河谷縱橫，丘陵區溝谷較為發育，暴雨中心多集中于流域的中上游地區。板橋流域面積502 km2,氣候為北亞熱帶濕潤、半濕潤氣候，多年平均降水量約為729 mm；板橋流域地形西北高東南低，夏季常產生局部暴雨；受地勢影響，洪水匯流迅速，多形成峰尖型瘦的洪水。

選取研究區2000—2010年汛期12場洪水數據進行模擬，其中2000—2007年8場洪水用于模型訓練，2008—2010年4場洪水用于模型測試，計算時間步長為1 h。

2 研究方法

2.1 模型方法

決策樹(decision tree，DT)是一種非參數監督學習方法，從測量特征與訓練數據推斷決策規則從而進行目標預測。決策樹自頂向下逐步生成，在生成模型結構時不斷建立分枝規則。目前常用的規則主要有兩種：基于信息增益的方法和基于最小基尼系數的方法。本文所采用的決策樹為分類回歸樹，分類回歸樹以基尼系數作為分枝規則，已在統計領域和數據挖掘技術中得到普遍應用。

隨機森林(random forest，RF)是一種基于決策樹的集成算法，效率較高，計算成本低，具有一定優勢。隨機森林的核心思想是構建多個未剪枝的DT集合。在模型訓練中，隨機森林在基于學習器構建Bagging集成的基礎上，引入了隨機屬性選擇，通過從結點的屬性集合中選擇屬性子集和最優特征，進一步增強了模型的泛化能力。

支持向量機(support vector machine，SVM)的主要特點是對原始數據集空間的超平面進行優化，找到具有最大間隔的劃分超平面。對于非線性樣本，SVM通過核函數進行非線性變換，將原問題映射到高維特征空間轉化為線性問題進行求解。

多層感知器(multilayer perceptron，MLP)是一種前饋人工神經網絡模型，解決了單層感知網絡對于非線性問題的弊端。MLP通過調節神經元間的連接權重和閾值，對神經網絡進行訓練。每個神經元計算n個輸入信號的加權平均后，應用非線性激活產生輸出信號。

2.2 評價指標

為了對比模型在不同流域洪水預報的適應性，本文采用相關系數(r)、納什效率系數(NSE)、均方根誤差(RMSE)、平均絕對誤差(MAE)、相對誤差(RE)幾種指標對模型模擬結果進行評價。其中，NSE反映了模型模擬的整體效果；RMSE和MAE兩個指標側重于評價系列總體的誤差情況，RMSE用來衡量觀測值與真值之間的偏差，MAE表達絕對誤差的均值程度，兩者都對序列中極大或極小誤差反應敏感；RE反映了誤差的相對大小，適應于非平穩序列的模擬比較；r是回歸模式中反映兩個變量相關程度的統計指標，可對模型擬合優度進行綜合評價。

2.3 洪水預報方案

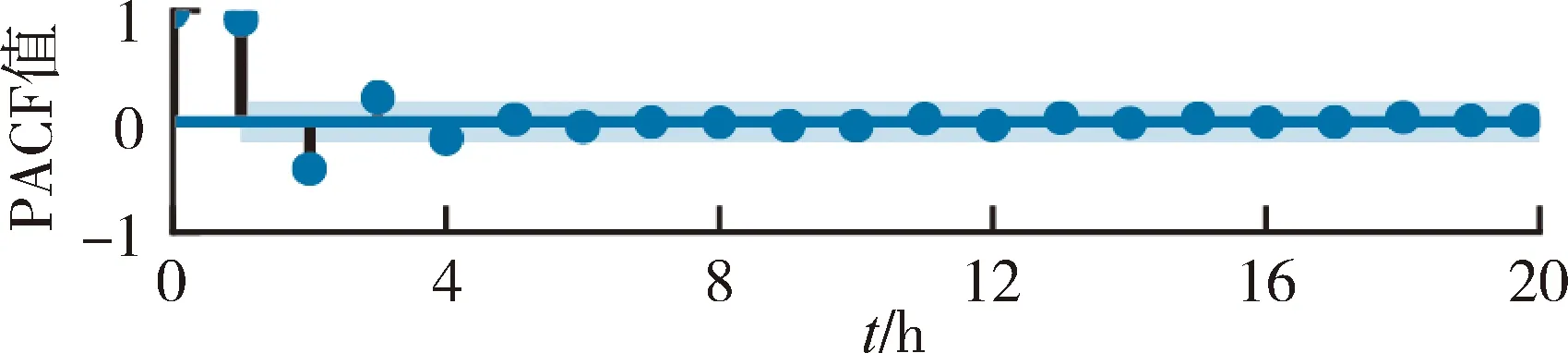
本文根據數據統計相關特性確定模型預報因子，通過流域偏自相關函數PACF構建模型的輸入結構。偏自相關函數消除了序列較短滯后條件產生的相關性影響，提供時間序列上兩個獨立點在不同滯時的相關性信息。圖2為3個流域的流量偏自相關曲線，在95%置信區間下選取流量輸入，與實時雨量數據共同構成模型的預報因子。模型結構如下：

Qt=f(Qt-Δt,Qt-2Δt,…,Qt-nΔt,R1t,R2t,…,Rmt)

(1)

式中：Q為水文站點流量；R為雨量站降水量；t為當前時刻；Δt為計算時段(本文取1 h)；n為流量滯后時段數；m為流域內的雨量站個數。板橋流域、馬渡王流域、志丹流域對應的流量最大滯時分別為 3 h、4 h 和3 h。

(a) 板橋流域

利用訓練期洪水預報因子分別訓練DT模型、MLP模型、RF模型和SVM模型，使用訓練好的模型對3個典型流域進行洪水滾動預報，并對模型模擬精度與適應性進行評價，主要步驟如下：

a. 劃分數據訓練期與測試期。采用2000—2010年汛期場次洪水數據，其中，2000—2007年數據用于模型訓練，2008—2010年數據用于模型測試。

b. 數據的歸一化處理。對訓練集和測試集數據進行標準化處理，消除數據的量級差異對模型模擬的影響，經過歸一化處理的數據位于0～1之間：

(2)

式中：xnorm為歸一化后的數據；x為原始數據；xmin、xmax為樣本每一維的最小值和最大值。

c. 模型訓練。選用基于高斯混合模型的TPE算法[21]進行模型參數尋優。使用訓練期樣本數據進行模型訓練，以RMSE作為目標函數，通過交叉驗證，計算最小誤差參數作為模型的最優參數。

d. 測試期洪水模擬與洪水滾動預報。利用訓練后的模型對測試樣本集進行預測。將當前時刻預測流量值作為下一時刻的前期流量輸入，以此類推，實現流域洪水的滾動預報。

e. 模型評價。使用相關系數、納什效率系數、均方根誤差、平均絕對誤差、相對誤差等指標對模型結果進行評價。

3 模擬預報結果與分析

3.1 模型模擬結果對比及誤差分析

根據模型的訓練結果對流域進行洪水模擬，整體來看，板橋流域和馬渡王流域4種模型均取得了較好的模擬結果，志丹流域的模擬結果相對較差。圖3和表1分別為模型測試期部分場次洪水模擬結果與誤差統計。可以看出，板橋流域和馬渡王流域洪水歷時較長，洪水過程皆呈現陡漲緩落的態勢。4種模型在以上2個流域模擬過程線趨勢理想，平均洪峰相對誤差為5%，平均洪量相對誤差為2%，平均峰現時刻誤差為2 h；志丹流域洪水過程呈現漲落快、歷時短的特點，模型在此流域模擬洪水的起漲點與實測洪水起漲點吻合較差，DT模型、SVM模型模擬洪峰偏小，MLP模型、RF模型洪峰則偏大，其中SVM在4種模型中模擬結果最好，平均洪峰相對誤差為7%，平均洪量相對誤差為12%，峰現時刻誤差維持在許可誤差3 h的范圍內。志丹流域模擬整體精度較低，這是由于志丹流域氣候干旱，產流的時空分布較復雜，同時洪水過程歷時較短，模型很難從洪水數據中學習到準確的水文信息，洪水模擬難度較大。

(a) 板橋流域2009082821號洪水

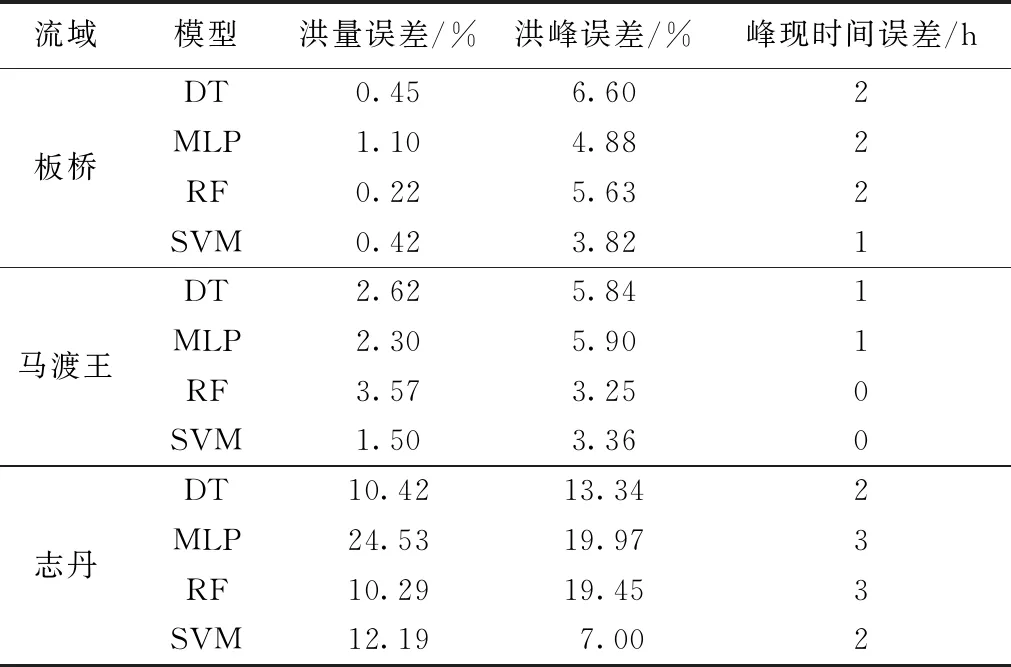
表1 測試期流域特征值模擬誤差

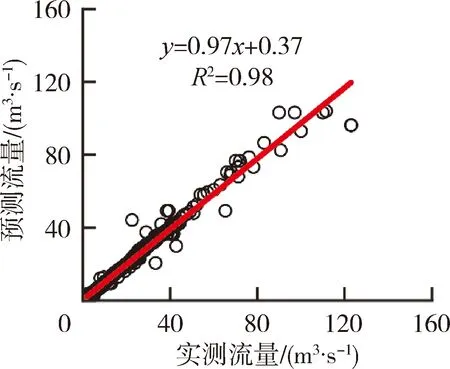
為了更加深入研究在半干旱與半濕潤區智能模型洪水模擬的適用性，對模型測試期的統計相關性水平與誤差分布進行評價。由模型測試期預測流量與實測流量散點圖(圖4)可以看出，板橋流域和馬渡王流域4種模型的擬合程度較好，志丹流域擬合程度較低。板橋流域和馬渡王流域模擬確定性系數均超過0.96，其中SVM模型模擬精度最優，確定性系數分別達到1.0和0.98，最接近1∶1線，流量模擬效果最好；志丹流域流量擬合相對較差。模型由優到劣分別為SVM、RF、MLP、DT，其中，SVM模型模擬精度最高，確定性系數達到0.7，DT模型模擬精度最差，確定性系數僅為0.48。

圖5為流域測試期模擬流量的相對誤差，半濕潤地區在模擬相對誤差水平上小于半干旱區。在半濕潤地區，模型模擬相對誤差由小到大分別為SVM、RF、DT、MLP，其中SVM模型整體相對誤差最小，平均相對誤差為2.98%。由于SVM模型根據樣本偏離值進行懲罰函數的調整，沒有考慮樣本數量的不平衡性，模型經過訓練所貯存的信息更多地反映了樣本數量較大的中小流量變化規律，因此，SVM模型對中小流量預報精度較高，在高流量時存在一定程度的低估。RF、DT、MLP模型在高流量時存在高估，其中RF、DT模型相對誤差水平相似(平均相對誤差分別為5.79%和7.50%)，MLP模型相對誤差較大，平均相對誤差值為22.54%；在半干旱區，模型模擬誤差較大，精度由高到低為DT、SVM、RF、MLP。4種模型流量模擬都存在高估，這是由于干旱區流量歷時短，洪水漲落迅速，模型對于洪水漲落點的捕捉較難，前期的高流量點極易影響后期模擬。

(a) 板橋流域(DT模型)

3.2 不同預見期下的模型穩定性分析

為了深入分析智能模型在洪水預報中的適應性，統計不同預見期(1～4 h)下的模型模擬結果(表2和表3)，對智能模型進行穩定性評估。

由表2和表3可見，當預見期為1 h時，在板橋流域，模型訓練期和測試期的模擬結果都較好(平均NSE為0.98)。訓練期模型模擬精度由大到小分別為DT、RF、MLP、SVM，其中DT模型RMSE為1.02，模擬結果最好，SVM模型誤差相對較大；測試期模型模擬精度由大到小分別為SVM、DT、RF、MLP，其中SVM模型在測試期模擬精度最高，MAE(0.28)和RMSE(1.08)均小于其他模型，DT模型和RF模型擬合程度和誤差水平相似，MLP則在4種模型中誤差最大。在馬渡王流域，模型在訓練期和測試期的模擬結果較好(NSE分別為0.99和0.97)。訓練期DT模型模擬精度最高，MAE(0.02)和RMSE(0.32)均小于其他模型；測試期SVM模型誤差最小，在洪水模擬中有較強的適應性。在志丹流域，模型模擬結果整體較差，訓練期的模擬結果優于測試期(NSE分別為0.84和0.51)。DT模型和SVM模型分別在模型訓練期和測試期取得了最大的精度。DT、RF、MLP模型在訓練期和測試期模擬結果差距較大，存在一定的過擬合問題，SVM模型在訓練期和測試期的模型模擬精度相近，具有一定的穩定性。

(a) 板橋流域

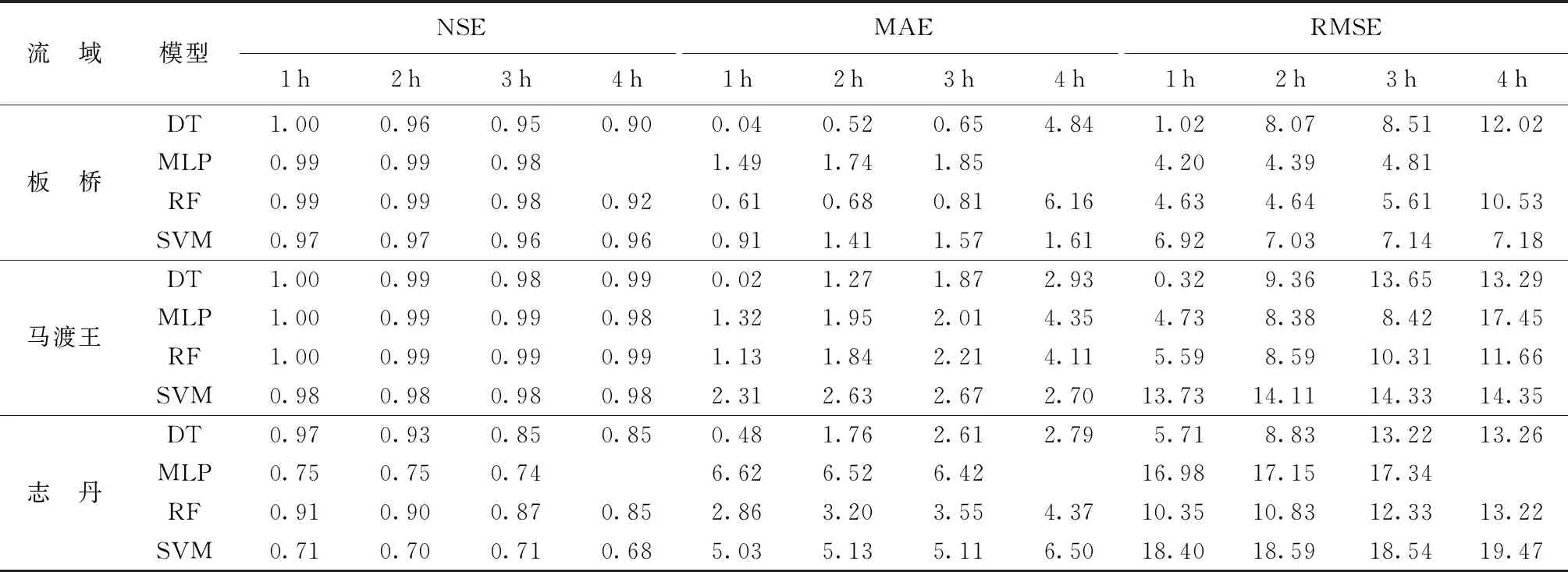
表2 訓練期不同模型不同預見期模擬結果

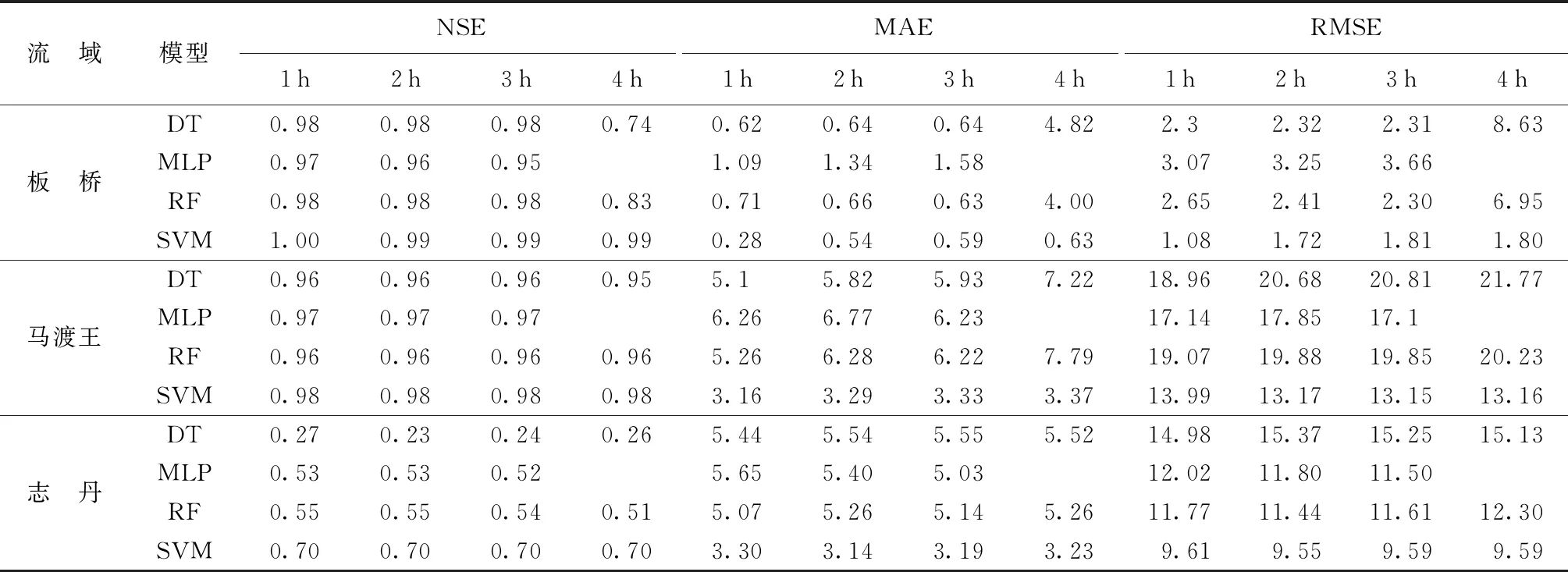
表3 測試期不同模型不同預見期模擬結果

綜合3個流域的預報結果，半濕潤區流域模擬結果優于半干旱區。訓練期DT模型模擬精度最高，但測試期模型模擬效果較差，這表明DT模型在實際運用中存在過擬合、泛化能力差等問題。SVM模型在訓練期的模擬結果相對較好，測試期模擬精度優于其他模型，泛化能力強，在洪水預報應用中有一定適應性。

可以看出，4種模型在短預見期下，均能保持較好的精度。隨著預見期的延長，模型的誤差累積增加。隨著預見期的延長，SVM模型在不同氣候區模擬結果均都能夠保持一定的穩定性；DT模型和RF模型模擬精度有所下降，但整體能滿足模型精度的要求，其中RF模型下降幅度較DT模型小；MLP模型在半濕潤區域較短預見期下能夠保持較好的模擬精度，隨著模型預見期的增長，模型性能出現驟降，模擬結果不穩定。

(a) 板橋流域

泰勒圖用于顯示不同模型模擬預測的河流流量在相關性、標準差和RMSE方面與實測值的接近程度，可對模型性能進行綜合評價。Moriasi等[22]的研究表明水文模型的RMSE小于數據標準差的50%，模型應用良好。圖6為在測試階段流域1～4 h預見期模擬結果的泰勒圖。在1～4 h的預見期內，DT、RF、SVM模型模擬精度略有下降，但仍保持了較穩定的模擬性能。MLP模型在1～3 h預見期內能夠保持一定穩定性，在4 h預見期模型性能驟降。

對于板橋流域和馬渡王流域，不同預見期模型模擬結果都較接近實測值，模型性能較好(除MLP_4 h外)，其中SVM模擬結果最接近實測值，模型結果最穩定。DT模型隨著預見期延長精度逐漸下降，在4種模型中穩定性最差(除MLP_4 h外)；志丹流域模型點在泰勒圖上較為分散，僅有SVM模型滿足比值小于0.5的界定要求，DT模型模擬結果遠離實測值，誤差較大。隨著預見期的延長，4種模型精度都有所下降，但不同預見期下模型精度的差異性小于不同模型選擇下的精度差異。

綜合3個流域不同預見期模型模擬結果，SVM模型在半干旱和半濕潤地區模擬都能得到較好的精度。隨著預見期的延長，模型精度有所下降，但模型整體穩定，在小流域實時洪水預報中具有明顯優勢。DT模型與RF模型模擬結果相似，能夠取得較好的精度，隨著預見期延長，模型精度下降，RF模型下降程度小于DT模型。這是由于RF模型是集成模型，在模型訓練中能夠更加全面地捕捉水文數據的復雜信息，較DT模型更具適應性。MLP模型在短預見期的洪水模擬中，能夠保持較好的精度，隨著預見期的延長，模型的穩定性驟變，模擬結果差。由于模型對數據精度要求大，對數據誤差敏感，在長預見期水文預報中需要及時對MLP模型模擬數據進行修正，從而保持模型的穩定運行。

4 結 論

a. 4種模型在半干旱與半濕潤區模擬結果差異較大，半濕潤區洪水模擬精度高于半干旱區。在半濕潤區，DT、RF、MLP、SVM模型模擬都可以得到較好的結果。在半干旱區，SVM模型的模擬精度較高，在洪水模擬中具有較強的適應性，其他模型模擬精度較差。

b. 隨著預見期延長，SVM模型模擬精度略微下降，但模型整體穩定，在小流域實時洪水預報中具有明顯優勢；DT模型與RF模型模擬精度緩慢下降，RF模型模擬精度下降程度略小于DT模型。MLP模型模擬精度隨預見期延長而驟減，模型穩定性差。由于模型對誤差敏感，在長預見期滾動預報中需要進行實時誤差校正。

c. 智能模型作為一種數據驅動方法可在洪水預報中發揮作用。在未來研究中，將洪水實時校正和模型集成技術與智能模型相結合，同時，針對半干旱地區產匯流條件復雜、洪水預報難的問題，可將下墊面信息引入智能模型輸入，進一步擴大模型的示范應用研究。