基于改進的可拓神經網絡的人防工程空氣質量評估方法的研究
王體春,張祥坤
(南京航空航天大學機電學院,江蘇 南京 210016)
1 引言
人防工程作為特殊時期人員掩蔽場所,對于空氣質量有較高的要求,這就要求在工程內部空氣質量較差時,及時進行通風處理。人防工程通風模式分為清潔式通風、濾毒式通風和隔絕式通風三種[1]。而使用哪種通風模式,或者這三種模式在什么情況下進行轉換,所依據的就是空氣質量評估結果。
目前,空氣質量評估方法種類眾多[2-3],主要有綜合指數評估法、模糊評估法、BP 神經網絡評估法等等。但是由于人們對人防工程的關注度不高,所以關于人防工程空氣質量評估方法還比較少。文獻[4]探討使用空氣質量綜合指數評估方法對空氣質量進行評估,但該方法計算模式固定,只是計算污染物濃度與對應的《環境空氣質量標準》規定的二級標準值之商的總和,當某種污染物濃度較高時,不能準確反映空氣質量狀況;文獻[5]使用灰色聚類及模糊評估方法對空氣質量進行評估,但此計算過程復雜,計算結果符合度還有待提高;文獻[6]使用BP 神經網絡對空氣質量進行評估,該方法準確度較高但由于BP 神經網絡神經元層數以及連接權數量較多,存在網絡結構復雜、訓練周期長的問題。
灰色管理聚類分析法可以用來研究“貧信息、小樣本”的不確定性問題,在污染物種類不完全明確的時候,能夠對已知污染物信息進行分析,發掘污染物之間隱含的關系[7-8]。相比于BP 神經網絡,可拓神經網絡僅有兩層神經元結構,在運算效率上更具優勢,并且也克服了BP 神經網絡訓練時間長、容易陷入非要求局限極值的缺點。可拓神經網絡非常適合用于研究區間分類問題,這為研究空氣質量級別劃分提供了新的解決方案[9-10]。將人防工程空氣污染物為研究對象,對基于灰色聚類和可拓神經網絡相融合的空氣質量評估方法進行了研究。使用灰色聚類原理依據空氣污染物關聯度對其進行分類并選取代表元素,然后使用可拓神經網絡空氣質量評估模型完成對空氣質量的評估,并結合實例驗證灰色聚類與可拓神經網絡在人防工程空氣質量評估中的可靠性和高效性。
2 人防工程空氣質量評估模型的構建
2.1 融合灰色聚類的人防工程空氣質量評估可拓神經網絡模型
人防工程內部空氣污染物成分比較復雜,影響因素眾多。具體來說,空氣污染物的成分及含量與人防工程的作用、所處位置、裝修狀況、管理維護效果、使用時長等有密切聯系。比如:作為民用地下停車場使用的人防項目,其空氣污染物主要為一氧化碳、二氧化碳、氮氧化合物等;地下商場、地鐵站等人員密集的人防工程中,二氧化碳、揮發性有機物、菌類等空氣污染物含量較高;裝修時間較短的人防工程,空氣會有甲醛、苯等污染物的出現。
研究的對象為人員掩蔽型人防工程項目,根據GB/T18883-2002《室內空氣質量標準》[16]規定,選取人防工程代表性的二氧化碳、一氧化碳、甲醛、揮發性有機物、氨、苯、氡氣七種空氣污染物作為空氣質量評估因子。使用防護工程空氣質量綜合監測儀對空氣污染物進行實時監測。借助網絡層,該設備能夠將檢測到的數據發送至云端服務器,以便應用層完成對數據的處理和保存工作。
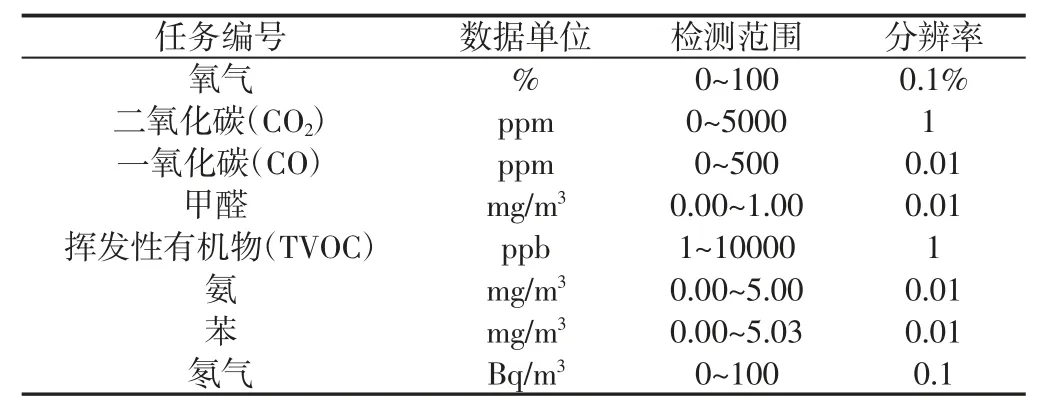
表1 防護工程空氣質量綜合監測儀的設備性能參數Tab.1 Equipment Performance Parameters of Protective Engineering Air Quality Integrated Monitor
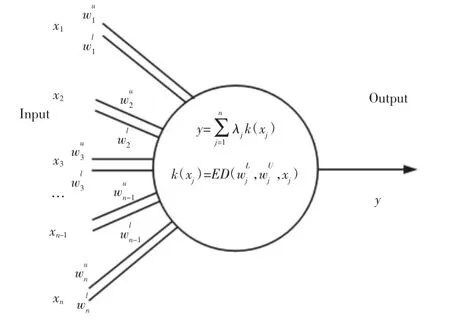
人防工程空氣質量評估模型,在可拓神經網絡結構的基礎上融合了灰色聚類理論,灰色聚類分析能夠簡化可拓神經網絡的結構,減少可拓神經元以及連接權的數量,融合灰色聚類后的空氣質量可拓神經網絡結構,如圖1 所示。
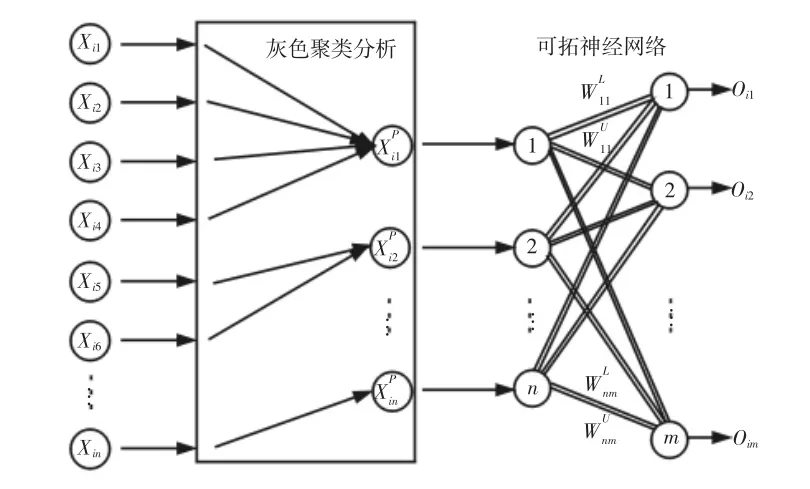
圖1 灰色聚類-可拓神經網絡空氣質量評估模型結構Fig.1 Grey Clustering-Extension Neural Network Air Quality Assessment Model Structure
灰色關聯聚類對已知污染物信息發掘其隱含關系的過程是一個無監督學習的過程,在空氣污染物種類不完全明確的時候,對空氣污染物進行聚類時可以不需要任何先驗知識,通過對樣本數據進行數據特征提取、關聯度計算、聚類劃分等操作完成對樣本數據分類。利用灰色關聯聚類分析將空氣污染物依照其內部關聯性分為若干類,然后從每一類污染物中選取一個樣本代表本類輸入到可拓神經網絡模型中對空氣質量進行評估。
可拓神經網絡將可拓學對事物的描述方法與神經網絡的并行計算、學習能力結合到一起,在處理區間分類、識別等問題方面有較大優勢。空氣質量評估可拓神經網絡模型采用有監督學習的過程,使用結果已知的數據對構建好的模型進行訓練,在不斷反饋、調整的學習過程中,空氣質量評估模型與數據樣本的契合度越來越高,當訓練模型收斂時,訓練過程結束,經過測試符合要求后便可用于空氣質量評估中。
2.2 空氣污染物初始序列建立與規范化處理
現假設從人防工程空氣污染物數據庫中提取m 個數據樣本,每個樣本存在n 種空氣污染物元素,樣本數據表示為:
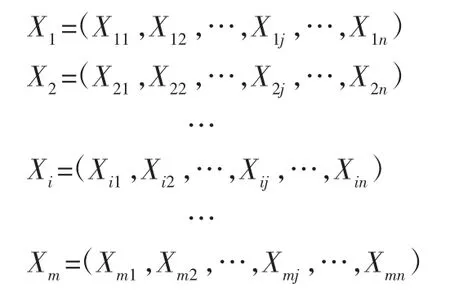
式中:i,j—整數,分別表示數據中第i 個樣本,樣本中第j 個元素。
由于不同種類的空氣污染物的描述單位不同,因此在含量數值上,不同污染物之間具有較大的差異。為避免因量綱的不同造成數據差別較大,在進行空氣污染物關聯聚類運算之前,需要對不同量綱的數據進行歸一化處理,采用的歸一化方法為minmax 歸一化方法,如式(1)所示。

歸一化處理后,所有數據的量值都會分布在[0,1]區間,方便后續的關聯度計算以及可拓神經網絡的收斂訓練。然后再對樣本數據進行始點零化處理:
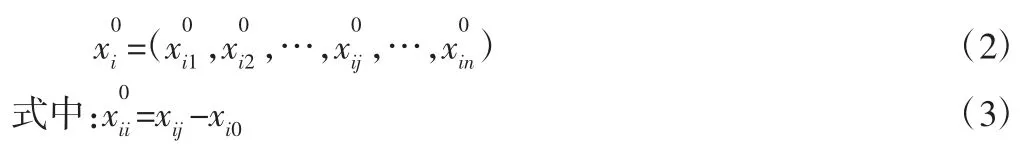
然后以人防工程空氣污染物類別為行、樣本序號為列構建樣本數據初始化矩陣,完成樣本數據初始序列的建立與規范化處理。
2.3 空氣污染物灰色聚類分析
空氣污染物灰色聚類分析就是運用灰色關聯理論來計算空氣污染物之間的關聯度,然后根據關聯度的大小對空氣污染物進行聚合分類。空氣污染物灰色聚類分析的第一步是要計算空氣污染物a、b 之間的絕對關聯度εab:
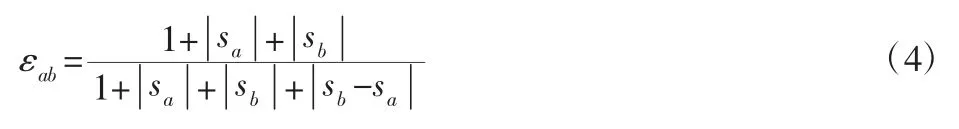
式中:a=1,2,…,m,表示污染物類別。
當a=b 時,表示a 和b 是同種污染物,故:

在式(4)中:

在求得全部的絕對關聯度之后,依照絕對關聯度下標構建空氣污染物關聯矩陣,如式(8)所示。關聯矩陣中的元素數值表示空氣污染物之間的聯系大小,數值越大表示對應的污染物關聯性越大。絕對關聯度大小是對空氣污染物進行聚類的依據。絕對關聯度的值域分布于[0,1]區間,一般情況下,當絕對關聯度值大于0.5 時,對應的空氣污染物之間就存在正向關聯性。
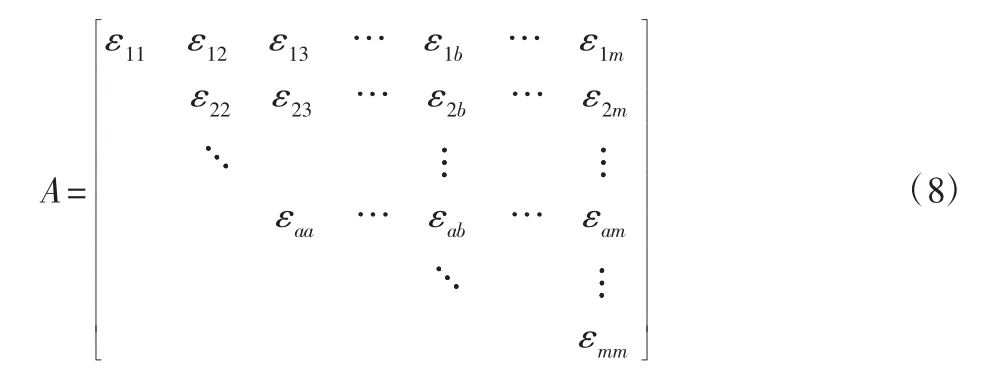
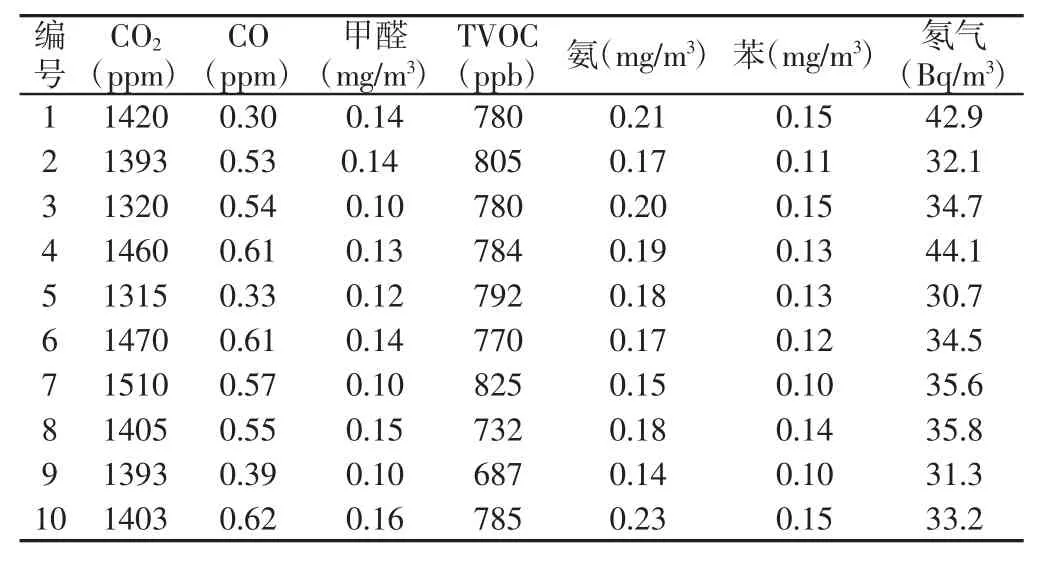
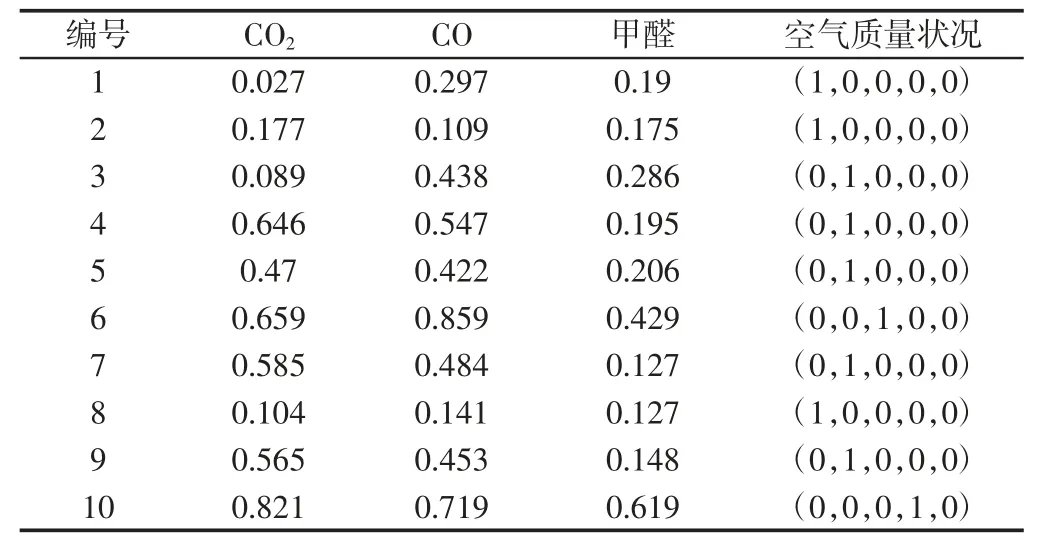
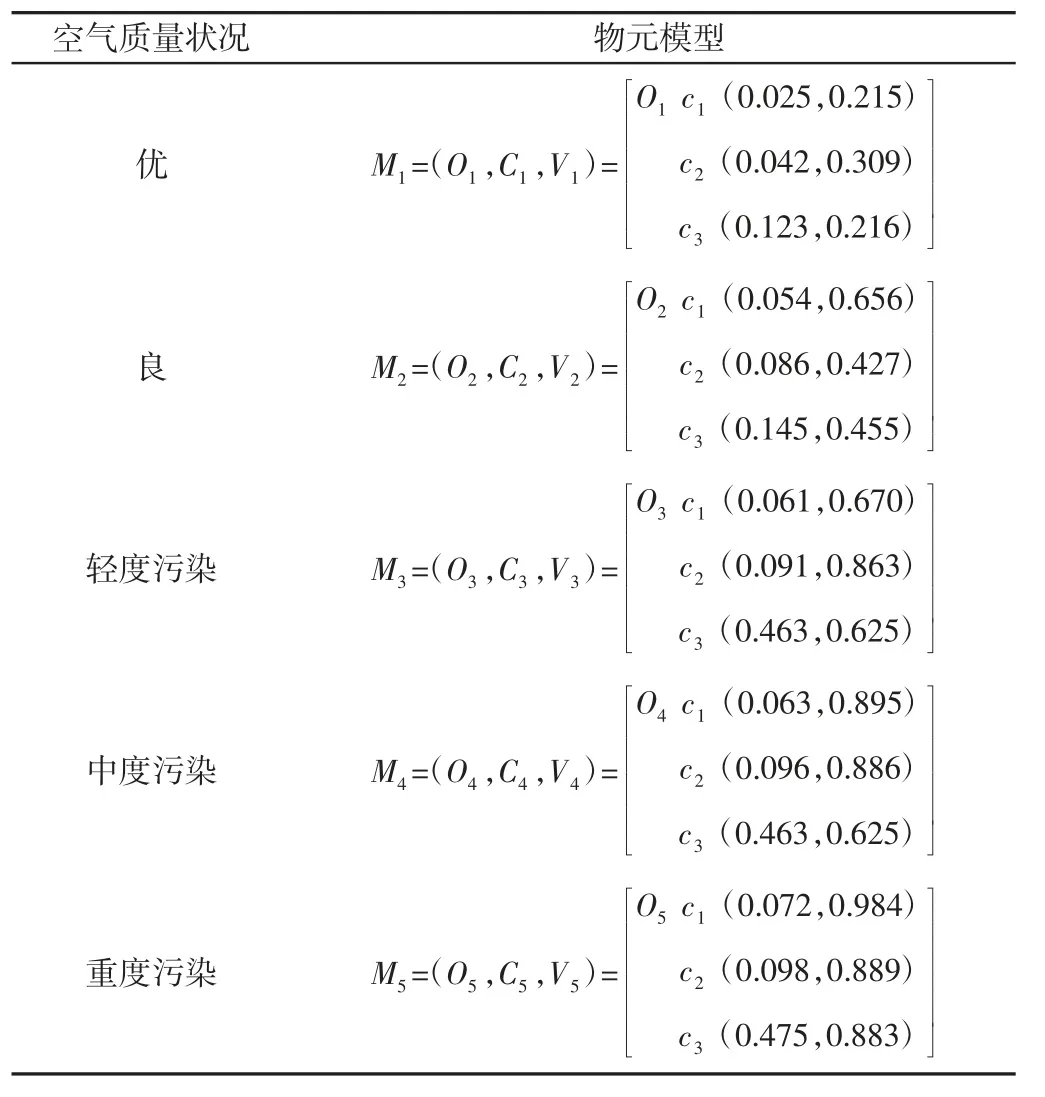
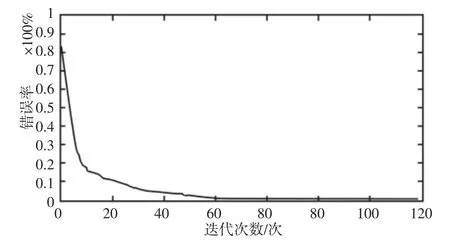
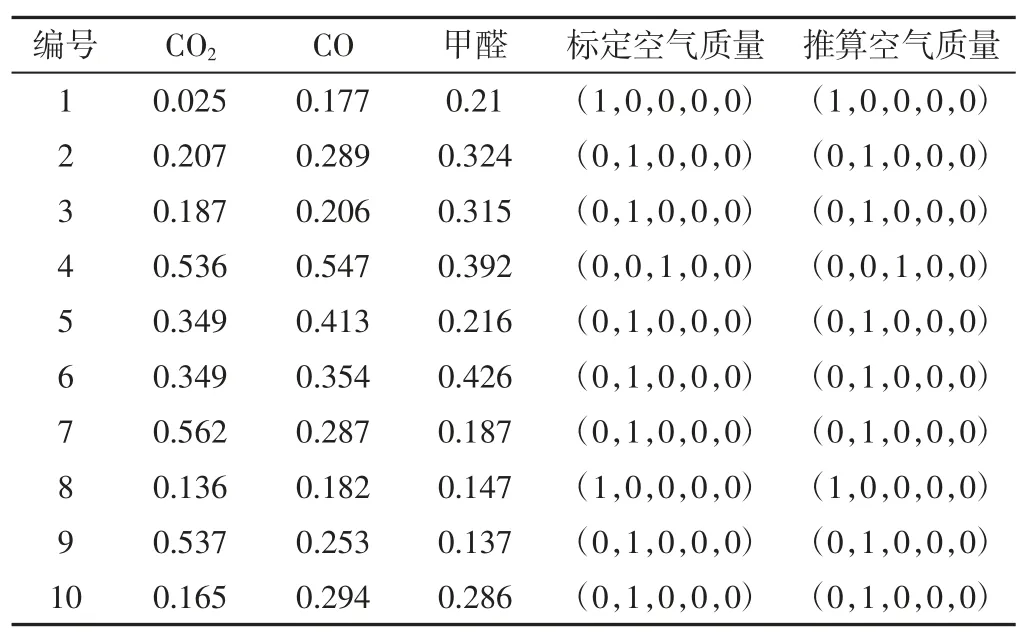
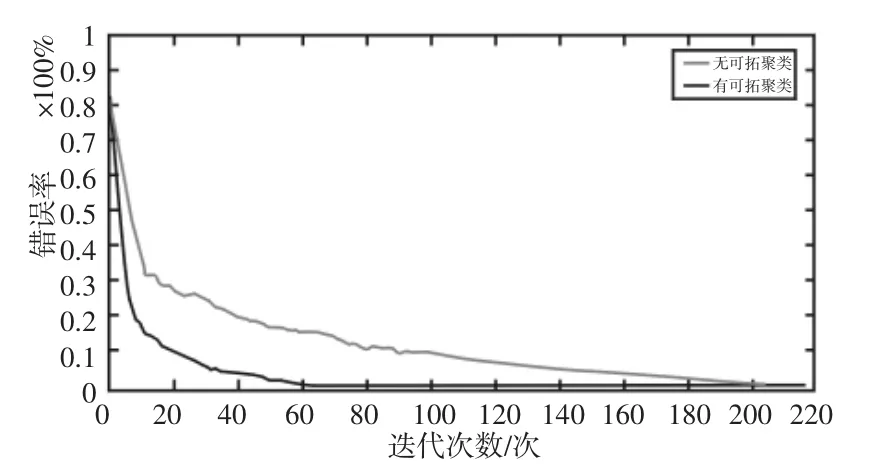
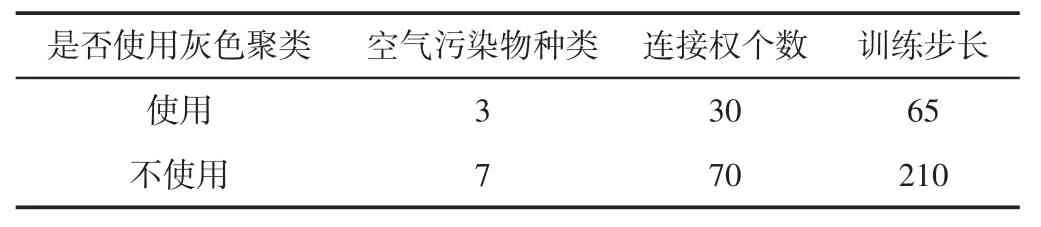
對空氣污染物進行聚類,首先就是要確定關聯度臨界值r 的值,r 的取值范圍一般為0.5 在根據實際需求確定r 值后,篩選出關聯矩陣中的每一個大于r 值的元素,并將這些元素所對應的空氣污染物做聚類處理,獲得空氣污染物的灰色聚類分析結果。然后計算每一類中所有空氣污染物相對GB/T18883-2002 規定的標準含量的比例,選取每一類中相對含量最大的空氣污染物代表本類參與空氣質量評估過程。相對含量計算公式為式(9)所示,其中C0為標準值。 可拓神經網絡只有兩層結構,包括輸入層與輸出層。輸入層神經元對應空氣污染物物元的不同特征值,輸出層神經元對應運算結果,在這里對應的是人防工程空氣質量評估級別。輸入層與輸出層之間利用雙權值進行連接,分別為對應特征經典域的上界和下界。例如,第i 個輸入層神經元和第j 個輸出層神經元之間的上界和下界可以用和表示。 可拓神經網絡結構中的神經元被稱為可拓神經元,它是組成可拓神經網絡的基本結構。可拓神元有多個參數輸入和一個結果輸出,每一個輸入參數都是一個物元變量,中間狀態為輸入信號的經典域的上界和下界表示,輸出結果 y,如式(10)所示。 圖2 可拓神經元結構Fig.2 Extension Neuron Structure 空氣質量評估其實質也是區間分類問題,可拓距是可拓神經網絡中一個重要的衡量工具,就是用來描述待測物體與目標區間中心的距離。在空氣質量評估中用來描述空氣污染程度與目標空氣質量區間的符合程度。對于某一個區間 由可拓距離表達式可以看出:無論是從哪個方向,當點x 趨近于區間 圖3 可拓距函數圖像Fig.3 Extension Function Image 根據是否存在外部訓練數據,雙權連接的可拓神經網絡可以分為有監督學習神經網絡和無監督學習神經網絡,這里使用有監督學習神經網絡。有監督學習神經網絡的訓練過程,即利用若干結果已知的樣本數據調節網絡訓練學習參數,使輸出結果與目標結果相符的過程。 假設有空氣質量已知的空氣污染物樣本集合X={X1,X2,,其中Np為空氣污染物樣本數量,則第i 條空氣污染物樣本數據表示為,其中n 為經過聚類分析簡化以后的空氣污染物數量,整個集合的學習誤差表示為Er=Nm/Np,其中Nm為總的訓練錯誤數。具體的過程為: 首先建立空氣污染物可拓物元模型用以表示可拓神經網絡輸入節點和輸出節點權值。 其次計算每種空氣質量對應的空氣污染物物元模型中的空氣污染物量值區間的初始中心。 式中:k—空氣質量對應的空氣污染物物元模型,k=1,2,…,n。i—物元模型中的空氣污染物類別i=1,2,…,nc。 如果有k*=p,使得EDik*=min{EDik},則按照如上過程進行下一次訓練,直到完成所有模式的訓練,否則更新權值和聚類中心后重新訓練。權值和聚類中心的調整方法如下所示。 更新第p 個空氣污染物樣本和k*的權值: 式中:η—學習效率。 更新第p 個空氣污染物樣本和k*的聚類中心。 最后如果聚類過程收斂并且總誤差符合要求,那么訓練完成,否則重復訓練過程重新進行訓練。 人防工程空氣質量評估的實現過程:首先,利用空氣污染物檢測傳感器檢測空氣污染物含量,同時將測量值上傳至云端數據庫保存;然后使用灰色聚類理論依據空氣污染物之間關聯度的大小對空氣污染物進行分類,并將聚類處理的數據傳入空氣質量評估可拓神經網絡模型中,對模型進行訓練;最后將檢測到的空氣污染物傳入訓練完成的空氣質量評估模型便可得到空氣質量評估結果。人防工程空氣質量評估模型框架,如圖4 所示。 圖4 人防工程空氣質量評估模型算法求解過程Fig.4 The Solving Process of an Air Defense Engineering Air Quality Assessment Model’s Algorithm 在人防工程空氣質量監測數據庫中,隨機抽取不同時間、不同測量地點的10 條測量數據,研究不同污染物之間內在關聯關系,如表2 所示。 表2 某人防工程空氣成分監測結果Tab.2 Monitoring Result about Air Composition of an Air Defense Engineering 首先,提取數據,并依據式(1)對數據進行歸一化處理。依據式(2)、式(3)對空氣污染物矩陣進行始點零化處理。然后,依據式(6)、式(7)求解 Sa,a=1,2,3,…,m。再根據式(4)、式(5)、式(8),可求得關聯矩陣A 為: 最后,依據樣本間的關聯程度對樣本進行分類。為保證樣樣本間具有較高的關聯度,關聯度臨界值r 應該大于0.6,但是r 值越大,樣本分類就越多,輸入可拓神經網絡中的特征向量及連接權數量就越多,可拓神經網絡就復雜,計算量就越大。所以r 關聯度臨界值r 的選取原則為:在能滿足可拓神經網絡運算準確度的同時,r 值越小越好。 根據相關經驗,此處選取關聯度臨界值r=0.7,若最終空氣質量評估結果準確度不符合要求再做調整。可以發現ε41、ε53、ε63、ε73、ε65、ε75、ε67的關聯程度較為緊密,也就是 X4與 X1屬于同一類,X3、X5、X6、X7屬于同一類,X2為一類。這七種污染物指標的聚類結果為{CO2、TVOC},{甲醛、氨、苯、氡氣},{CO}。經由查閱資料可以知道,空氣中的CO2和揮發性有機物與人防工程中的人員活動有關;甲醛、氨、苯、氡大多來源于工程裝修以及家具等散發的污染物;CO 有可能是來自于工程外部,汽車尾氣排放產生的污染。 經過聚類分析以后,將七種污染物依照其關聯性分為三類。每一類中的污染物可能來自于同一污染源,同類中污染物含量的增減具有關聯性。因此后面評估空氣質量時只需從不同類中各提取一個代表性污染物進行研究即可,這樣可以在保證研究結果不失真的同時減少空氣污染物監測成本以及相關工作量。 經過灰色關聯聚類分析,七種空氣污染物來源按照關聯度可以分為人員活動相關、工程裝修相關、工程外部侵入三類,現根據式(9)從每一類中各取一個指標,以CO2、CO、甲醛代表這三類空氣污染物對空氣質量進行分析。 在人防工程空氣質量監測數據庫中,按照優、良、輕度污染、中度污染、重度污染五種空氣質量級別,對每個級別隨機抽取100 條數據,并做歸一化、規范化處理。相關數據,如表3 所示。 表3 某人防工程空氣質量監測數據(部分)Tab.3 Monitoring Data about Air Composition of an Air Defense Engineering(Partial) 可拓學物元模型能夠從物、物的特征、特征的值三個方面清晰的描述事物各項指標之間的關系和變化。使用物元理論構建以Om為對象,Cn為對象特征,Vn為特征量值的物元模型 Mm=(Om,Cn,Vn)。在該物元模型中,Om(m=1,2,…,5)為對應的五種空氣質量狀況;Cn(n=1,2,3)空氣質量的影響因素,在此處表示CO2、CO、甲醛;Vn表示各影響因素對應的取值區間。空氣質量評估物元模型,如表4 所示。 表4 空氣質量評估物元模型Tab.4 Matter Element Model about Air Quality Assessment 圖5 空氣質量評估模型訓練誤差變化趨勢Fig.5 Air Quality Assessment Model’s Training Error Trend 由空氣質量評估模型訓練誤差變化趨勢圖可以看出,訓練誤差在初期急速下降,隨著訓練迭代次數的增加,訓練誤差逐步趨近于0。當訓練迭代次數在65 次時,訓練誤差低至0.005 左右,可拓神經網絡已完成收斂,訓練過程結束。 表5 模型預測結果評定(部分)Tab.5 Evaluation of Model Predicted Result(Partial) 在可拓神經網絡訓練完成之后再從人防工程空氣質量監測數據庫中抽取100 條數據用作驗證訓練模型的準確性,新抽取的數據不包含之前的訓練數據。對測試數據進行歸一化處理后輸入訓練模型,其標定的空氣質量和評估的空氣質量,如表5 所示。可以看出,推算結果與標定結果相符,準確率達到98%,可以將該模型用于空氣質量評估中。 若不使用灰色聚類理論對空氣污染物進行聚類處理,將所有類別空氣污染物都輸入可拓神經網絡空氣質量評估模型對其進行訓練,訓練過程總誤差變化趨勢與使用灰色聚類理論的訓練誤差變化趨勢對比,如圖6 所示。 圖6 灰色聚類的使用對提升模型訓練效率的對比圖Fig.6 Comparison of the Use of Grey Clustering to Improve the Misuse Efficiency of Model Training 由圖6 可以看出,使用灰色聚類處理后的可拓神經網絡空氣質量評估模型在訓練迭代次數達到65 次時就已經收斂,而不使用時,訓練迭代次數在210 次時才完成收斂。詳細對比情況,如表6 所示。與不使用灰色聚類相比,在空氣質量評估準確度相差無幾的情況,使用灰色聚類處理能大幅減少空氣質量評估可拓神經網絡模型中的神經元個數以及連接權數量,縮短訓練時長,對模型運行效率上有較大提升。 表6 灰色聚類的使用對模型訓練誤效率的影響Tab.6 The Effect of the Use of Gray Clustering on the Mis-Efficiency of Model Training 主要工作如下:(1)研究使用可拓神經網絡模型構建人防工程空氣質量評估的方法。(2)引入灰色關聯聚類理論,簡化人防工程空氣質量評估模型復雜程度,并對該理論引入前后的空氣質量評估結果做出對比。 研究結果表明:①使用灰色關聯聚類對空氣污染物進行聚類預處理,能夠減少輸入可拓神經網絡中的污染物種類數量以及可拓神經元連接權的數量,對可拓神經網絡運算量的簡化以及收斂速度的提升有明顯效果。②關聯度臨界值r 對人防工程空氣質量評估結果有影響作用,r 值越大,對模型的簡化效果越小,空氣質量評估準確度越高,反之亦然。在實驗中可以不斷調整r的大小,在能滿足模型評估準確度的同時,r 值越小越好。 使用灰色關聯聚類理論對人防工程空氣質量評估模型進行優化,可以確保人防工程空氣質量評估模型在保持較高評估準確度的同時提高模型的運算效率,對人防工程空氣質量分析具有現實的意義。
2.4 空氣質量可拓神經網絡模型


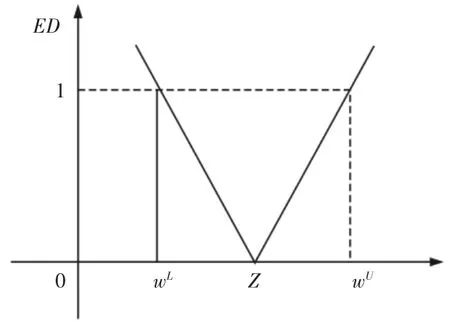
2.5 空氣質量可拓神經網絡模型
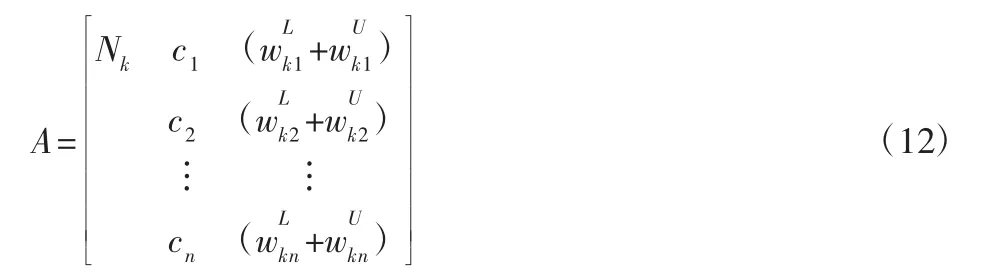


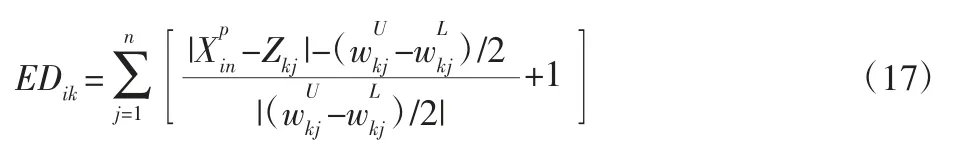
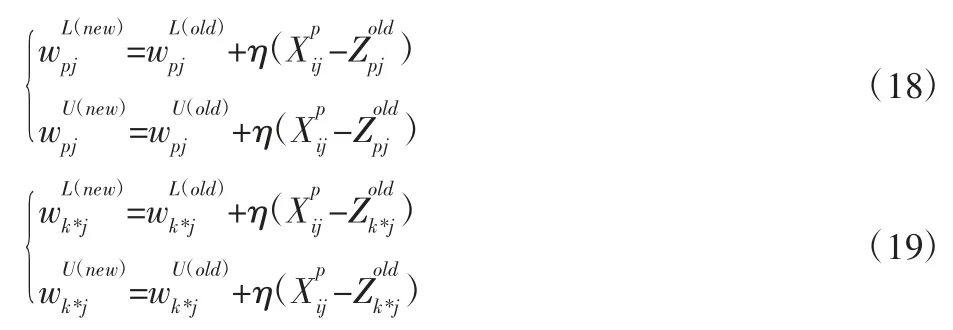

3 空氣質量模型算法求解過程
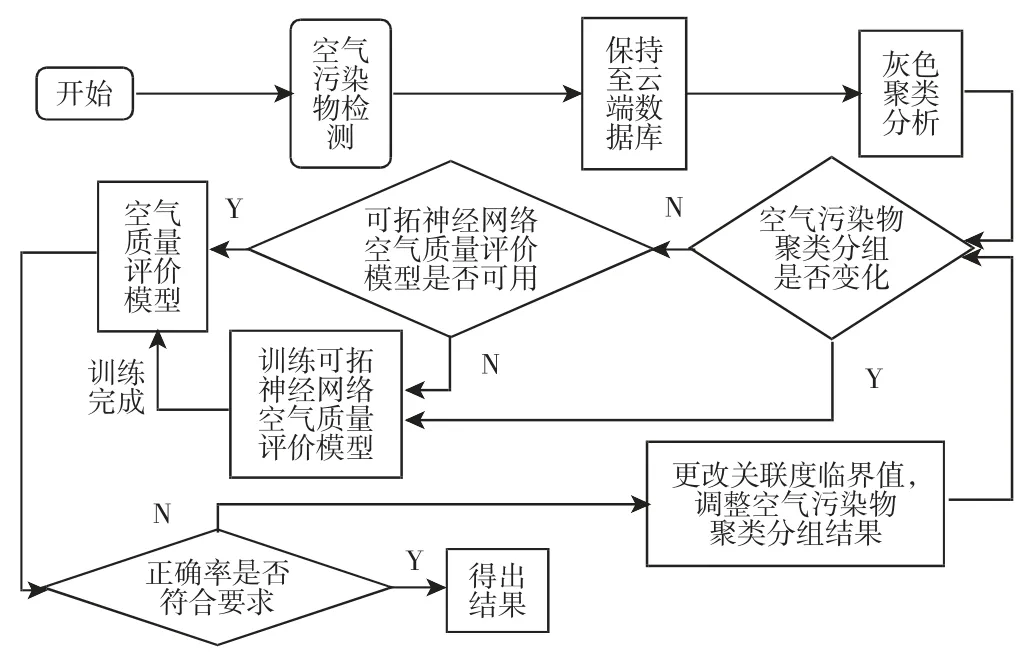
4 人防工程空氣質量評估案例
4.1 空氣污染物的灰色關聯聚類模型構建

4.2 可拓神經網絡模式訓練
4.3 人防工程空氣質量評估模型測試
5 結論

