顧及多因子影響的中國西部地區大氣加權平均溫度模型精化研究

莫智翔 黎 杏 黃良珂 劉立龍 韋欣怡 周清華

1 桂林理工大學測繪地理信息學院，桂林市雁山街319號，541006 2 廣西空間信息與測繪重點實驗室，桂林市雁山街319號，541006

近年來，隨著全球導航衛星系統(global navigation satellite system，GNSS)在氣象學上的發展，GNSS水汽探測因相較于傳統的水汽觀測手段具有高時空分辨率、低成本、全天觀測、高精度等優勢，成為國內外專家學者研究的熱點。在地基GNSS數據反演大氣水汽(precipitable water vapor，PWV)的過程中，水汽轉換系數K是將對流層天頂濕延遲(zenith wet delay，ZWD)轉化為大氣水汽的關鍵參數[1]，主要受大氣加權平均溫度(Tm)的影響[2-3]。

目前，加權平均溫度的計算模型可根據是否需要測站處的氣象信息分為兩類：第1類是需要地表氣象參數的經驗模型，這種模型一般需要實測的地表溫度(Ts)等氣象參數。其中，Bevis模型[4]是目前使用最廣泛的模型之一，它首先探究Ts與Tm之間的線性關系，建立適合于中緯度地區(27°～65°N)的Bevis模型，但該模型應用到其他區域會存在明顯的系統性偏差[5]。為此，不少學者對基于局部或全球多年Tm數據擬合的經驗模型進行研究[6-8]，并對Bevis經驗模型進行改進，在地表氣象參數可獲得的情況下，這類Tm模型的效果最優。第2類是不需要氣象參數的Tm模型[9-11]，這類模型是基于局部或全球多年Tm數據擬合的經驗模型，使用簡單，但相比于采用實測地表氣象信息的Tm模型，其精度不是很高。其中，Emardson模型[12]是直接利用測站緯度和年積日計算Tm的非氣象參數模型，姚朝龍等[13]和劉立龍等[14]將Emardson模型分別在中國低緯度地區和新疆地區進行精化，并取得良好的效果。由于中國西部地區地形起伏大，Tm變化顯著，現有模型在該地區的適用性較差[15]。實際大氣中,大氣溫濕廓線是千變萬化的，在我國西部地區的GNSS水汽遙感中采用Bevis模型不能獲得最優的計算效果，因此利用當地的氣象資料對GNSS水汽反演中的Bevis模型進行修正是很有必要的。

本文在分析中國西部地區Tm與高程和地面溫度相關性的基礎上，利用探空數據對Bevis模型進行改進，建立一種與測站高程、地面溫度和季節變化有關的Tm模型，并對其精度進行驗證。

1 數據來源及計算原理

選取中國西部地區45個探空站2014～2016共3 a的實測數據，數據采樣間隔為12 h。數據可從美國懷俄明州立大學的網站免費下載(http//weather.uwyo.edu/upperair/sounding.html)，各探空站的分布如圖1所示。

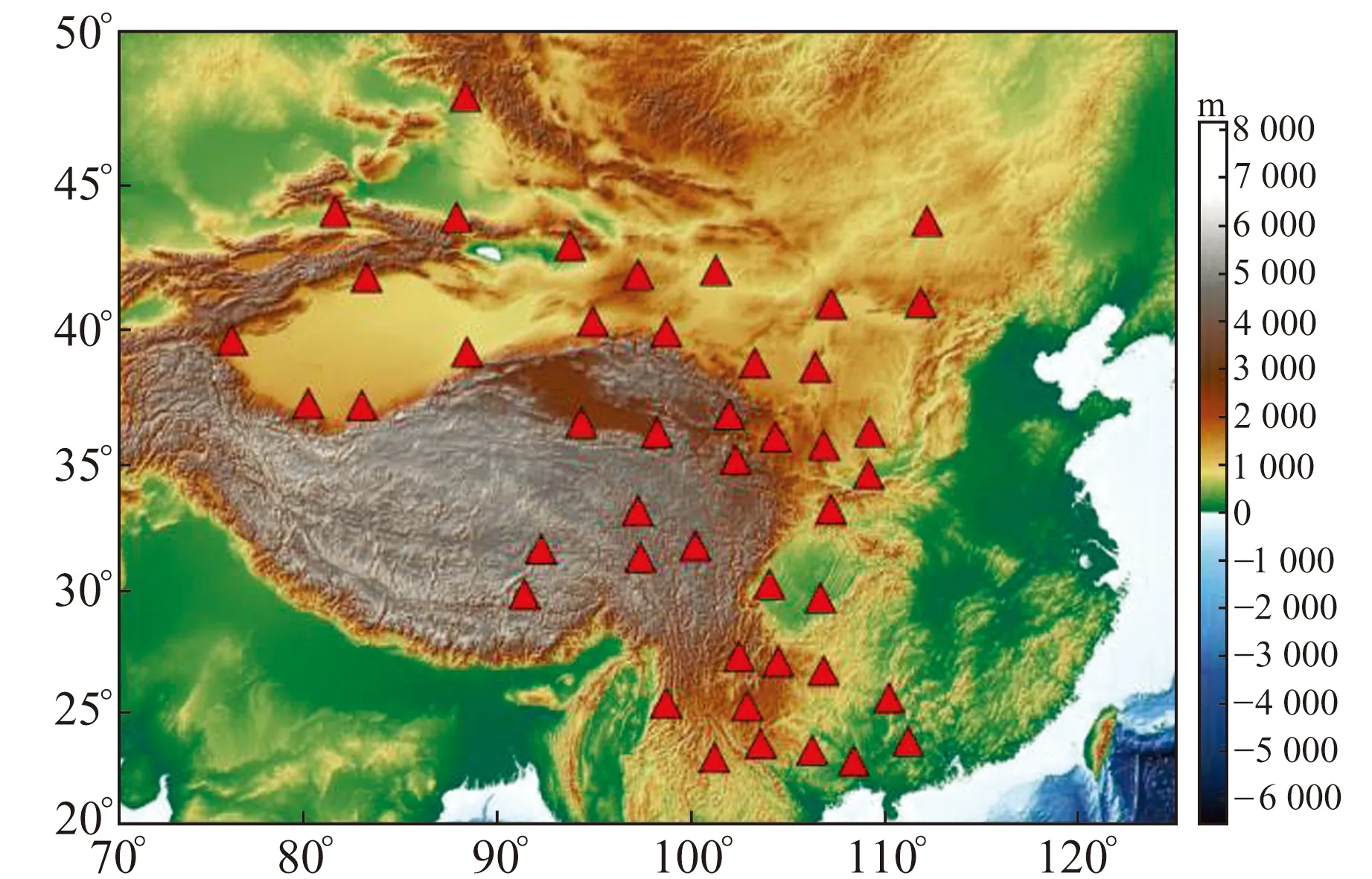
圖1 中國西部地區45個探空站點位分布Fig.1 Distribution of the 45 radiosonde stations in western China

探空站資料分為大氣分層數據和地表數據，其中分層數據包含氣壓、溫度、露點溫度、相對濕度等相關氣象數據，地表數據包括大氣可降水量和測站的位置等信息。根據不同的等壓面，由數值積分法計算探空站Tm值是目前國內外學者公認的最為精確的方法，其具體計算過程見文獻[3]。由于Tm是由測站上空水汽壓和絕對溫度沿天頂方向的積分求得的，對于缺乏探空資料的地區，Tm很難精確求得，所以通常是根據區域探空數據采用統計回歸方法擬合出Tm與地面溫度Ts的關系式。其中，較為經典、常用的是Bevis等[16]的Tm-Ts線性回歸公式：

Tm=70.2+0.72Ts

(1)

另外，B?hm等[10]提出的GPT2w模型是目前全球范圍內較為先進的經驗對流層格網模型，具有1°和5°格網分辨率，可提供包括Tm在內的多種對流層參數。GPT2w模型使用時只需輸入目標點的位置和相應日期，就可以得到目標點處的Tm值。本文分別將1°分辨率和5°分辨率的GPT2w模型簡稱為GPT2w-1和GPT2w-5。

2 中國西部地區大氣加權平均溫度模型的建立

2.1 大氣加權平均溫度與高程、地面溫度相關性分析

中國西部地區經緯度范圍廣、地形起伏大，影響Tm的因素很多，其中Tm與高程[3]及Ts[4]有一定的相關性。為探究中國西部地區Tm與高程的關系，本文選取2015年該地區45個探空站數據，利用數值積分法計算出Tm值，并與相應測站高程的相關性進行探究，結果如圖2(a)所示；為探究中國西部地區Tm與Ts的關系，以2015年桂林探空站(25.33°N，110.3°E)數據為例，進行Tm和Ts的相關性分析，結果如圖2(b)所示。

圖2 Tm與相應測站的高程和Ts的相關性分析Fig.2 The correlations analysis between Tm and height, Tm and Ts in corresponding stations

由圖2(a)可以看出，Tm與高程的變化呈相反趨勢，即海拔越高，Tm越低，二者呈負相關關系。由此可見，考慮Tm的高程變化并對其進行改正是準確計算Tm的關鍵。由圖2(b)可以看出，Tm與Ts的變化呈相同趨勢，即Ts越高，Tm越高，二者呈正相關關系，且具有較強的相關性。因此，在建立Tm模型時可以考慮加入Ts因素。

2.2 模型的建立

研究表明，實測獲取的Tm與模型計算的Tm的殘差序列存在明顯的周期性[17]，對該殘差序列進行建模，并對模型計算的Tm進行補償，根據獲取的Tm來源的不同，可建立不同的補償模型。本文在對Tm進行建模時，考慮了Tm具有年周期和半年周期變化的特點，經過上述分析可知，Tm不僅與Ts呈線性正相關關系，而且與季節和高程也有密切關系，因此，本文在Bevis模型的基礎上加入季節和高程因素，建立了一種新的Tm模型關系式：

(2)

式中，Ts為測站溫度，doy為年積日，a1、a2、a3、a4、a5、a6和a7均為模型系數，h為測站高程。

本文利用中國西部地區45個探空站2014～2016年觀測數據中各測站的大氣加權平均溫度Tm、地面溫度Ts和測站高程來確立新模型的系數。首先利用數值積分法計算中國西部地區每個探空站的Tm值，然后通過代入相應的Tm、Ts和測站高程數據，利用式(2)擬合計算得到中國西部地區新Tm模型系數值，結果如表1所示。

表1 使用中國西部2014～2016年的探空數據計算的新Tm模型系數

在應用該模型時，只需將目標處的地面溫度Ts、年積日和高程(單位m)代入模型，就可得到所需的加權平均溫度Tm。

3 新Tm模型精度驗證

為驗證本文構建的新Tm模型精度，采用2017年探空站數據獲得的Tm作為參考值對新模型進行精度分析。采用偏差(bias)和均方根誤差(RMS)作為精度評價指標，其表達式為：

(3)

(4)

3.1 基于探空數據的模型精度分析

利用中國西部地區45個探空站2017年數據資料獲取的Tm作為參考值，驗證新模型的精度，同時分別與廣泛應用的Bevis模型和目前性能較優的GPT2w對流層模型進行對比分析，計算并統計bias和RMS，結果如表2、圖3和4所示。

由表2可知，在中國西部地區Bevis模型表現出明顯的正偏差，其年均值為1.87 K；GPT2w-1模型和GPT2w-5模型均表現出明顯的負偏差，年均值分別為-2.06K和-2.68K，說明Bevis模型和GPT2w模型在中國西部地區計算Tm時均存在明顯的系統偏差。而新Tm模型的最大、最小偏差分別為2.76 K和-3.94 K，平均偏差為-0.08 K，與另外3個模型相比偏差較小。同時，GPT2w-5模型表現出最大的RMS，其平均值為4.9 K，而GPT2w-1模型與Bevis模型精度相當，表明GPT2w-1模型的精度優于GPT2w-5模型。新Tm模型的平均RMS為3.89 K，其精度比Bevis模型提高了約0.65 K (14.3%)，與GPT2w-5模型和GPT2w-1模型相比分別提高了1.01 K (20.6%)和0.4 K (9.3%)，說明新Tm模型在中國西部地區相比于其他3個模型有較高的精度，且比其他模型穩定。

表2 利用2017年探空站資料檢驗Bevis模型、GPT2w模型及新Tm模型的精度統計

圖3 利用2017年探空資料評估中國西部地區新Tm模型、GPT2w模型及Bevis模型的年均bias分布Fig.3 Distribution of annual bias for new Tm model, GPT2w model and Bevis model assessed using radiosonde data from 2017 in western China

由圖3可知，Bevis模型在西部地區出現明顯的正偏差，GPT2w-1模型和GPT2w-5模型則表現出明顯的負偏差；而新Tm模型與Bevis模型相比，在青藏高原地區的偏差更趨穩定，這是由于青藏高原大部分地區的地表高程較大，Bevis模型的估計精度會隨海拔的升高而逐漸降低[18]，而新Tm模型則對這一誤差進行了修正。在中國西部地區，新Tm模型的絕大部分bias絕對值小于4 K。總體而言，新Tm模型在中國西部地區有較小且穩定的偏差。

由圖4可知，在西部地區，Bevis模型、GPT2w-5模型和GPT2w-1模型均表現出較大的年均RMS，這是由于GPT2w模型在計算Tm時未考慮高程，而且未對日偏差進行改正，因此在地形起伏較大的中國西部地區表現出較大的偏差[3]。而新Tm模型在中國西部絕大部分地區的RMS小于5 K，相比于GPT2w模型和Bevis模型，其年均RMS更趨于穩定，進一步說明新Tm模型在計算中國西部地區Tm值時相較于其他模型有明顯的改善，特別是在地形起伏較大的地區，具有較好的精度。由此可見，新Tm模型在中國西部地區表現出良好的精度和穩定性。為進一步驗證新Tm模型、GPT2w-1模型、GPT2w-5模型和Bevis模型的精度，對中國西部地區45個探空站的年均bias和RMS進行統計，結果見圖5。

由圖5可知，新Tm模型的bias明顯比其他3個模型的小且穩定；GPT2w-1模型和GPT2w-5模型與新Tm模型及Bevis模型相比表現出明顯的負偏差，而新Tm模型的bias在零周圍分布更均勻。新Tm模型及Bevis模型的RMS分布比GPT2w-1模型和GPT2w-5模型集中，而新Tm模型的RMS分布范圍比Bevis模型小，進一步表明新Tm模型的性能比其他3種模型穩定。新Tm模型的精度比Bevis模型、GPT2w-1模型和GPT2w-5模型高，更適用于高低起伏大、地形復雜的中國西部地區。為檢驗不同模型的季節性表現，本文對每個模型進行日偏差檢驗，統計不同模型的bias和RMS，結果如圖6所示。

圖5 利用2017年探空資料評估中國西部地區不同模型的年均bias和RMS分布直方圖Fig.5 Distribution histogram of annual bias and RMS for different models assessed using radiosonde data from 2017 in western China

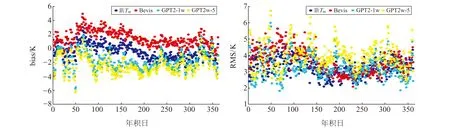
圖6 利用2017年探空資料評估中國西部地區不同模型的日均bias和RMS分布散點圖Fig.6 Scatter diagram of daily bias and RMS for different models assessed using radiosonde data from 2017 in western China

從圖6可以看出，新Tm模型受季節的影響要明顯小于另外3種模型，在全年期間較為平穩。Bevis模型的偏差和變化幅度在夏季最低，春、冬季最高，而且在多天的精度檢驗中發現，新Tm模型的精度要高于Bevis模型，特別是在春、冬季，2種模型的精度對比較明顯，進一步說明在同樣受季節變化的影響下，新Tm模型要優于Bevis模型。在全年期間，雖然GPT2w模型考慮了Tm的季節性變化，但由于受系統誤差的影響，GPT2w-5模型和GPT2w-1模型都表現出明顯的負偏差，并且在春、冬季觀察到較大的值。特別是GPT2w-5模型，由于空間分辨率比GPT2w-1模型低，其偏差和RMS變化較為明顯；而在多數時間，新Tm模型均顯示出較小的偏差，并且沒有明顯的季節性變化。就RMS而言，所有模型均顯示出相對明顯的季節性變化，春季和冬季的RMS相對較大，夏季的RMS較小。這是因為大多數選定的探空站位于中緯度地區，夏季Tm變化較小，冬季Tm變化較大,影響了Tm的計算。此外，在大多數時間里，新Tm模型的RMS比其他模型小且穩定，顯示出優越的季節性能。總之，與其他模型相比，考慮季節性變化的新Tm模型明顯提高了Tm的計算精度。

大量研究表明，Tm的變化與高程具有較強的相關性。為分析Bevis模型、新Tm模型、GPT2w-1模型和GPT2w-5模型計算Tm的bias、RMS與高程的變化關系，本文對45個探空站進行分類，按高程小于500 m、500～1 000 m、1 000～1 500 m、1 500～2 000 m和大于2 000 m分別進行歸類，結果見圖7。

圖7 利用2017年探空資料評估中國西部地區不同模型的bias和RMS隨高程變化統計Fig.7 The statistics with height variations of daily bias and RMS for different models assessed using radiosonde data from 2017 in western China

由圖7可知，GPT2w-1模型和GPT2w-5模型在每個高程范圍內均表現出顯著的負偏差，Bevis模型在大于500 m的高程范圍內表現出顯著的正偏差，而在小于500 m的高程范圍內表現出負偏差，說明隨著高程的增加，Bevis模型的系統誤差越來越明顯，不適用于高原地區Tm的計算。而新Tm模型在不同高程范圍內均表現出相對較小甚至不顯著的偏差。此外，GPT2w-1模型和GPT2w-5模型在500～1 000 m高程范圍內表現出較大的RMS，Bevis模型在大于2 000 m的高程范圍內也表現出較大的RMS，而新Tm模型在每個高程區間內的RMS都較小且較為均勻。由圖7還可以明顯看出，4種模型都有較大的RMS，但總體來說，新Tm模型的RMS要小于其他3種模型，進一步說明新Tm模型的精度表現更好。

3.2 Tm對GNSS-PWV估計的影響

建立中國西部地區新的Tm模型是為了提高Tm的計算精度，其最終目的是提高GNSS反演PWV的精度。但一般情況下，GNSS基準站與探空站不在同一地址，且大多數GNSS基準站主要用于大地測量研究，未安裝氣象傳感器，所以難以全面、可靠地研究Tm對GNSS-PWV計算的影響。為此，本文采用Huang等[19]提出的計算Tm對GNSS-PWV影響的方法(式(5))，并對計算結果進行分析：

(5)

式中，RMSPWV為PWV的RMS，RMSK為轉換系數K的RMS，RMSTm為Tm的RMS，RMSPWV/PWV為PWV的相對誤差，其中Tm和PWV采用年均值計算。RMSPWV和RMSPWV/PWV用于評估模型計算Tm的誤差對其計算GNSS-PWV的影響，各模型RMSPWV和RMSPWV/PWV的計算結果如表3所示。

表3 利用2017年探空站資料檢驗Bevis模型、GPT2w模型及新Tm模型計算PWV的理論RMS誤差和相對誤差統計

由表3可知，GPT2w-5模型表現出較大的RMSPWV和RMSPWV/PWV，最大值分別為0.92 mm和5.22%。而新Tm模型的RMSPWV小于0.55 mm，平均值為0.22 mm；新Tm模型的RMSPWV/PWV平均值為1.43%，范圍為0.85%～1.93%，比其他模型小且穩定。因此，用新Tm模型計算Tm帶來的誤差對GNSS-PWV的影響比其他模型小且較穩定，可以為中國西部地區GNSS-PWV估計提供更為準確的Tm。

4 結 語

1)本文選用2014～2016年45個探空站數據，利用回歸分析方法建立適用于中國西部地區的多因子加權平均溫度模型(新Tm模型)，并以2017年探空站獲取的Tm作為參考值，計算的平均bias和平均RMS分別為-0.08 K和3.89 K。

2)通過將新Tm模型與Bevis模型和GPT2w模型相比較可知，由于建模時顧及了Tm的季節性變化和高程變化，新Tm模型相比于Bevis模型和GPT2w模型在中國西部地區的平均偏差和RMS更小，精度更高，受高程及四季變遷的影響較小，對西部地區有著更好的適用性和穩定性。

3)從理論上分析各模型計算的Tm誤差對GNSS-PWV估計的影響，得到新Tm模型的RMSPWV和RMSPWV/PWV的平均值分別為0.22 mm和1.43%，比其他模型更小、更穩定。

總之，新Tm模型得到的Tm精度可靠，可以滿足中國西部地區GNSS水汽探測的要求，能進一步改善中國西部地區GNSS大氣水汽反演的精度，更好地服務于中國西部地區氣象學研究工作。