基于優化支持向量機的隧道涌水量預測

蘇 昭

(陜西鐵路工程職業技術學院，陜西 渭南 714000)

0 引 言

隧道突涌水問題是其施工過程中的一種常見災害，不僅會造成施工工期延誤，還可能造成人員傷亡及財產損失，進而開展隧道涌水問題研究具有較強的必要性。目前，在隧道涌水災害的研究成果中，隧道涌水量預測是一個熱點問題，已被相關學者進行了研究，如李顯偉在隧道涌水影響因素篩選的基礎上，利用層次分析法構建了隧道涌水量預測模型，合理指導了現場施工；徐承宇利用數值模擬分析了隧址區的水文地質條件，進而實現了隧道涌水量預測，并對比模擬結果和現場監測成果，得到兩者具有較好的一致性，驗證了模擬方法的有效性；雷波等、楊卓等和廖志泓均以BP神經網絡為基礎，構建了隧道涌水量預測模型，且預測結果與實際情況較為一致，進而驗證了該預測模型的有效性。上述研究雖取得了一定的研究成果，但其研究均未涉及支持向量機在隧道涌水量預測中的應用，加之隧道所處位置的區域性特征，進行有必要進一步開展隧道涌水量預測研究。因此，該文以支持向量機為理論基礎，利用試算法和粒子群算法優化模型參數，進而構建出參數優化后的隧道涌水量預測模型，以便更好的指導現場災害防治。

1 基本原理

該文預測模型主要包含兩個階段，其一，是模型參數的優化過程，即先以試算法確定最優核函數，再利用粒子群算法優化支持向量機的懲罰系數；其二，是涌水量的預測過程，即以現場監測樣本為基礎，對隧道涌水量進行預測研究，以驗證該文預測模型的有效性。

1.1 支持向量機

支持向量機是一種統計學方法，其預測過程中是將樣本信息從映射至高維空間，進而得到全局最優解，不僅具有結構風險最小化，加之其泛化能力較強，適用于隧道涌水量預測。若隧道涌水量樣本為{xi，yi}，可將其線性回歸函數f(x)表示為

f(x)=ωφ(x)+b

(1)

式中：ω為權值向量；φ(x)為輸入信息的高維空間映射函數；b為偏置量

如前所述，支持向量機的預測過程具有結構風險最小化，且為弱化誤差ε，引入松弛變量ξi、ξi*，兩者均是不小于零的常數，進而可將上述回歸映射問題優化為

(2)

(3)

式中：C為懲罰因子；ε為超出誤差

同時，以對偶理論為基礎，可對上式進行二次規劃，即

(4)

(5)

式中：K(xi，yj)為核函數；αi、αi*為拉格朗乘子

通過上式的優化求解，可得到支持向量機的預測函數為

(6)

1.2 模型參數優化

上述預測過程雖能實現隧道涌水量預測，但在其預測過程中，核函數和懲罰因子對預測結果的影響較大，進而為避免兩參數對預測結果的影響，有必要對兩者進行參數優化處理，結合相關文獻的研究成果，將兩參數的優化過程分述如下。

(1)核函數優化

核函數控制著輸入信息向高維空間映射的內積運算，進而對預測精度具有重要影響。同時，支持向量機的核函數類型共計有四類。

線性核函數，該函數的表達式為

k1(xi,xj)=xixj

(7)

多項式核函數，該函數的表達式為

k2(xi,xj)=(xixj+1)d

(8)

式中：d為正整數

徑向基核函數，該函數的表達式為

(9)

式中：γ為徑向基參數

Sigmoid型核函數，該函數的表達式為

k4(xi,xj)=tanh[β(xixj)+c]

(10)

上述四種核函數的預測效果各有差異，為保證預測精度，該文提出通過試算法來確定最優核函數，即對四種核函數的預測效果進行對比分析，預測精度最優者即為最佳核函數。

(2)懲罰因子優化

懲罰因子是影響支持向量機預測精度的另一因素，對其優化具有較強的必要性。同時，鑒于粒子群算法的全局最優能力，該文利用其優化懲罰因子，優化過程為：對粒子進行初始化，即設置其權重因子、迭代次數等；對粒子個體的適應度值進行計算，并與全局極值進行對比，若前者更優，則用其替換全局極值，反之，保留全局極值；對粒子位置及速度進行更新，并重復計算其極值；如此循環往復，直至達到期望或迭代次數?；诹Ｗ尤核惴ǖ幕驹?，將其優化流程總結如圖1所示。

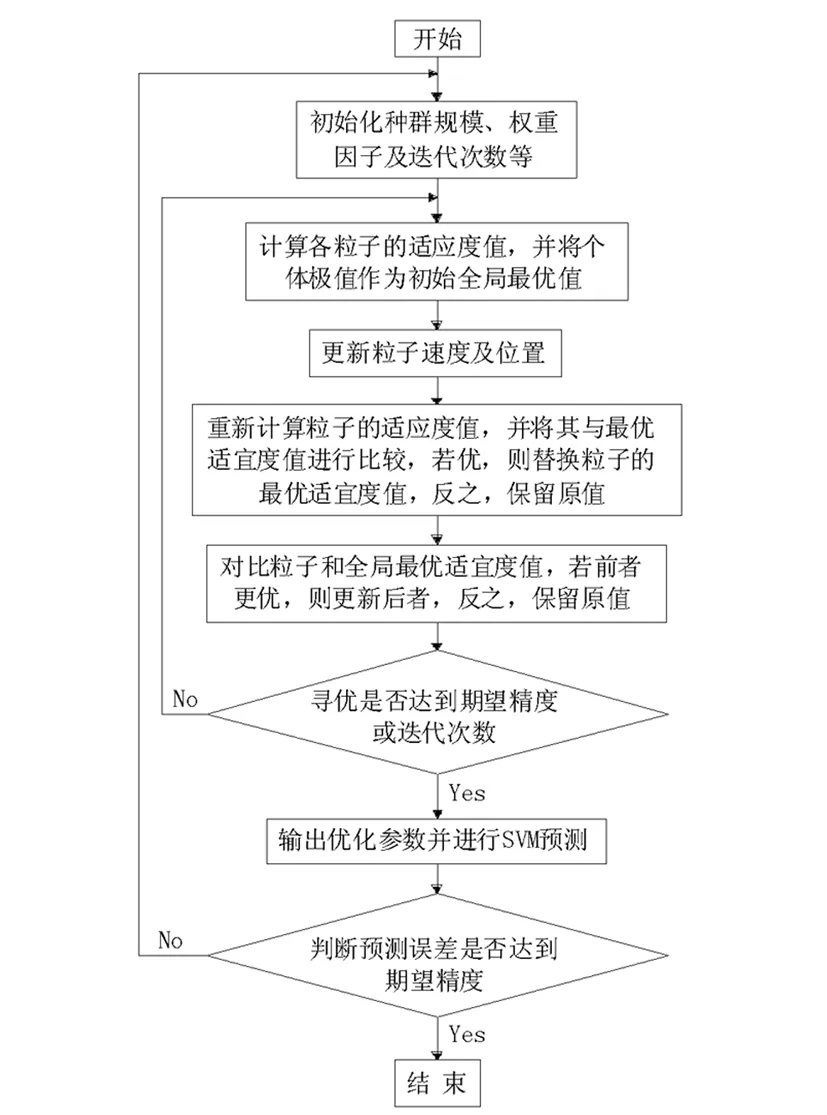
圖1 粒子群算法優化過程示意圖

如前所述，通過上述試算法和粒子群算法可有效優化支持向量機的模型參數，且為便于后期描述，將核參數優化過程命名為初步優化階段，將進一步的粒子群優化過程命名為PSO-SVM模型預測。

2 基本原理

2.1 工程概況

富家山隧道隸屬于汾西縣富家山村，走向間于66°～83°之間，采用分離式設計，左線略短于右線，且兩者的相關特征參數如表1所示；同時，該隧道左、右線的最大埋深均大于100 m，其中，左線最大埋深為120.00 m，對應里程樁號為ZK35+130；右線最大埋深為131.30 m，對應里程樁號為K35+782。

根據勘察成果，隧址區巖性相對較為單一，主要由奧陶系中統峰峰組、上馬家溝組的灰巖和白云巖組成，圍巖整體完整性相對較差；同時，區內雖未見斷裂發育，但背斜構造發育，且隧址區主要位于背斜軸部，進而也降低了隧道的完整性。受地質構造及巖性影響，區內地下水主要由孔隙水和巖溶水組成，前者富水性較差，且與隧道施工無明顯水力聯系，進而可忽略其對隧道施工的影響；巖溶水則對隧道施工影響較大，據區域水文資料，區內巖溶水較為發育，加之施工情況，隧道施工過程中的涌水災害頻發，進而開展該隧道的涌水量預測研究具有重要意義。

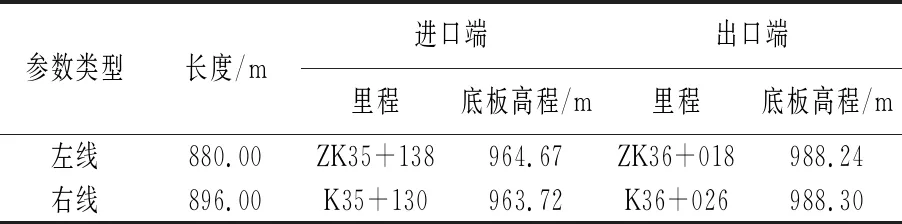
表1 左、右線特征參數統計

同時，根據文獻的研究成果可知，隧道涌水受多種因素影響，其中，圍巖完整性、破碎帶導水能力、破碎帶距頂板的距離、裂隙水壓力和隧道埋深等因素的影響尤為顯著，進而該文在預測過程中，以上述五個影響因素作為預測模型的輸入層。在隧道現場施工過程中，隧道發生了多次涌水事故，通過現場統計，得到左、右線各12組涌水樣本，且為避免不同輸入元素單位信息對預測結果的影響，對上述五個影響因素進行歸一化處理，具體如表2所示。

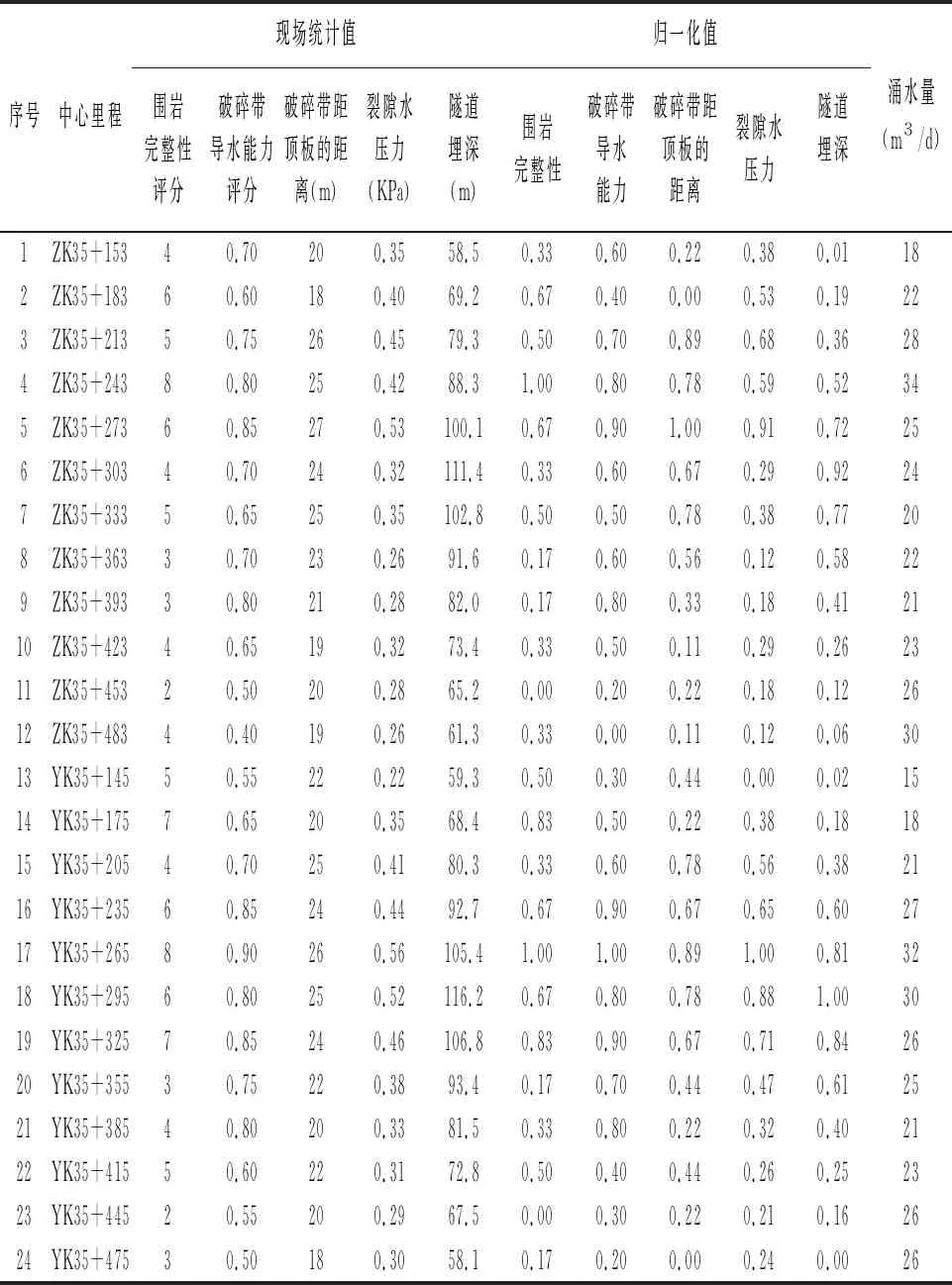
表2 隧道涌水樣本統計

2.2 涌水量預測分析

根據前述論文思路，先利用試算法對四種核函數進行優化篩選，且提出以訓練時間和平均相對誤差為評價指標來判斷各核函數的預測效果，前者用時越短，說明預測模型具有相對更優的模型結果；后者越小，說明預測模型的預測精度相對越高。同時，在篩選過程中，先以左洞9～12號樣本為驗證樣本，其余樣本為訓練樣本。

通過訓練及預測，得到四種核函數的預測結果如表3所示。由下表可知，不同核函數的預測效果存在明顯差異，進而驗證了對其進行篩選的必要性。根據預測結果，在訓練時間方面，Sigmoid型核函數的用時相對最少，進而其運算速度相對最快，其次是徑向基核函數、多項式核函數和線性核函數；在預測精度方面，同樣以Sigmoid型核函數的平均相對誤差最小，其值為2.18%，徑向基核函數相對次之，而線性核函數和多項式核函數的預測精度相當，但明顯差于前兩者。因此，基于訓練時間和平均相對誤差的綜合評價，確定該文模型的核函數類型為Sigmoid型。

表3 不同核函數的預測效果統計

為進一步提高預測精度，再利用粒子群算法優化支持向量機的懲罰因子，其優化結果如表4所示。在相應預測樣本處，對比粒子群算法優化前后的結果可知，通過粒子群算法的參數優化，相對誤差均不同程度的減小，進而說明粒子群算法可有效提高預測精度；同時，PSO-SVM模型的最大、最小相對誤差分別為1.31%和1.10%，平均相對誤差僅為1.22%，得出PSO-SVM模型具有較高的預測精度，達到了期望值，也驗證了該模型在隧道涌水量預測中的作用。

表4 左洞預測結果統計

同時，為進一步驗證該文模型的有效性，該文再以右洞21～24樣本為可靠性樣本，對其進行預測，以研究該文預測模型的可靠性。類比前述預測過程，得到右洞的預測結果如表5所示。由表5可知，通過粒子群算法的優化，各驗證樣本的預測精度均不同程度的提高，且右洞預測結果的最大、最小相對誤差分別為1.43%和0.98%，平均相對誤差僅為1.19%，進一步驗證了粒子群算法在支持向量機參數優化中的有效性，也說明該文PSO-SVM模型具有較強的可推廣性和可靠性，適宜于隧道涌水量預測。

表5 右洞預測結果統計

通過前述優化過程闡述及左、右洞的優化預測，得出PSO-SVM模型具有較高的預測精度，驗證了該模型的有效性，為隧道涌水量預測提供了一種新的思路。

3 結 論

通過優化支持向量機模型在隧道涌水量預測中的應用，主要得出如下結論：

(1)傳統支持向量機的參數確定具有一定的主觀性，進而在預測過程中有必要對模型參數進行優化預測，其中，試算法可優化篩選支持向量機的核函數，而粒子群算法可很好的優化支持向量機的懲罰因子。

(2)PSO-SVM模型在隧道涌水量預測中的相對誤差值均小于2%，說明其具有較高的預測精度，適用于隧道涌水量預測，且該預測模型具有很好的可靠性，值得進一步的深入推廣應用研究。

(3)鑒于不同隧道所處地質條件、施工條件的差異，建議在該文模型的應用過程中應充分結合現場工程條件，確定合理的輸入層信息，并依據模型優化過程，實時篩選優化參數，以保證預測結果的準確性。