基于深度增強學習的海克斯棋博弈算法研究
鄭博宇
北京信息科技大學 北京 100085
引言
海克斯棋,也稱作六貫棋[1],最初在丹麥報紙Politiken發表的一篇文章里出現,當時稱Polygon。1948年,John Nash卻又將其重新獨立發明出來,而熱衷于此的玩家們隨即就將其稱作Nash。稍后1952年Parker Brothers發行了一個版本,將其稱為Hex,從此這個名字就固定了下來。六貫棋通常使10×10或11×11的菱形棋盤,而JohnNash 采用的卻是14 × 14 的棋盤。
海克斯棋的規則如下:
(1)一共兩人參與海克斯棋博弈,棋盤由紅藍兩色組成。棋盤邊緣分別填上雙方顏色;
(2)雙方輪流下棋,一次只能下一棋子,且僅占領一處空格,在空格上方放上屬于自己顏色的棋子;
(3)在比賽的過程中,禁止吃棋子的行為;
(4)第一個把棋盤兩端屬于自己顏色的棋盤邊緣連通成一條線的人獲勝。
1 深度強化學習的算法模型設計
深度強化學習Deep Q-Learning是將Q Learning與CNN卷積神經網絡相結合,實現了從感知到動作的端到端的革命性算法。普通的Q-learning算法中,當項目的狀態和動作空間是離散且維數不高時可使用Q-Table儲存每個狀態動作對的Q值,但是在海克斯棋的博弈過程中,13×13的棋盤狀態和動作空間是高維連續時,使用Q-Table過于龐大,建立起來十分困難。本文將海克斯棋類博弈與Deep Q-learning深度增強學習算法結合起來,使得該棋類的博弈能力不斷提升。
1.1 Q learning 算法的結構
Q Learning是一種在強化學習算法中基于value-based的算法。Q即為Q(s,a),Q(s,a)在某一時刻的 s 狀態下(s∈S),采取 動作a (a∈A)動作能夠獲得收益的期望,通過Q值進行學習,而環境將會根據agent的動作反饋相應的回報reward r,所以本算法的主要思想是將State與Action構建成一張Q-table來存儲Q值,再根據Q值來選取能夠獲得最大的收益的動作。Dlearning的更新方式,推導函數如下:
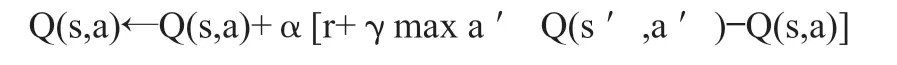
上式更新公式,根據下一個狀態s’中選取最大的 Q ( s ′, a ′ ), Q(s’,a’)值乘以衰變γ加上真實回報值最為Q現實,而根據過往Q表里面的Q(s,a)作為Q估計。
1.2 深度增強學習的算法流程設計
為了使得算法性能更穩定,DQN中存在兩個結構完全相同但是參數卻不同的網絡,一直在更新神經網絡參數的預測Q估計的網絡MainNet和參數固定不動預測Q現實的神經網絡TargetNet。Q ( s , a ; θ i ) Q(s,a;θ_i) Q(s,a;θ i)表示當前網絡MainNet的輸出,用來評估當前狀態動作對的值函數;Q(s,a;θi?) Q(s,a;θ^?_i) Q(s,a;θi?) 表示TargetNet的輸出,可以解出targetQ,初始時刻將MainNet的參數賦值給TargetNet,然后MainNet繼續更新神經網絡參數,而TargetNet的參數固定不動。再過一段時間將MainNet的參數賦給TargetNet,如此循環往復。這樣使得一段時間內的目標Q值是穩定不變的,從而使得算法更新更加穩定。
2 界面以及算法的實現
2.1 界面實現
根據海克斯棋棋譜[3],本棋的棋盤是一個由11×11個六邊形組成的棋盤。具體界面如圖2所示。根據海克斯棋的規則和特點,使用PyQt5實現海克斯棋人機博弈軟件。棋盤由11×11個六邊形棋格組成,坐標原點在最下面正中間,坐標分別從11到1,從K到A。該軟件具備區分先手后手,輸出棋譜、悔棋等博弈基本功能。
2.2 卷積神經網絡實現
博弈項目采用Theano構建和訓練卷積神經網絡。網絡架構來自于谷歌DeepMind在AlphaGo中采用的架構網絡結構,該結構由十個卷積層和一個完全連接的輸出層組成。
過濾器使用六邊形以更好地觀察棋局的局部性。通過對方形濾波器應用Theano的卷積運算,即可生成六角濾波器。每個卷積層共有128個過濾器,由直徑3和直徑5六角形組成。每個卷積層的輸出是簡單的直徑5和直徑3的填充輸出。輸出使用sigmoid函數,其余所有的激活函數都是ReLU。網絡的輸出對應相應位置的動作價值的矢量。且網絡依舊會評估不可移動和棋子已經下過的位置。
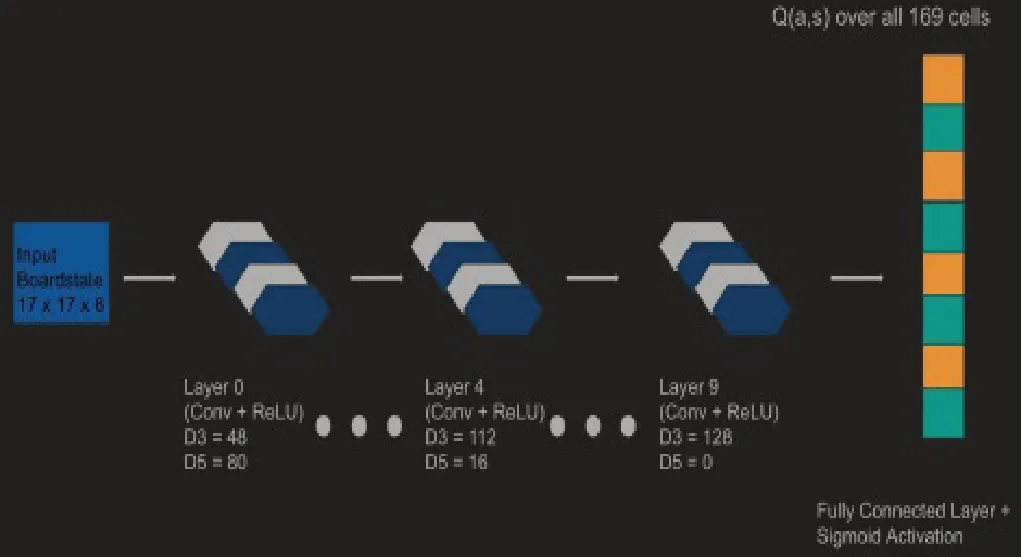
圖3 卷積神經網絡圖
其中D3表示直徑為3的濾波器的數量,D5表示所示圖層中直徑為5的濾波器的數量。
2.3 深度強化學習算法的實現
初始化replay memory M, Q-network Q,和狀態D,執行相應的博弈次數,S為從D開始的位置,根據先手后手下棋。當棋局沒有結束,a = epsilon greedy policy(s, Q),snext = s.play(a),如果游戲結束則r=1,沒結束r=0。M.add entry((s,a,r,snext)),(st,at,rt+1,st+1) = M.sample batch() ,targett = rt+1 ? max a Q(st+1)[a]。對Q執行梯度下降步降低(Q(st)[at]? targett)2, s = s.play(a)。在海克斯棋項目中,深度增強學習采用greedy policy(s, Q)的策略算法,直接采取具有最大Q值的動作作為當前策略,小部分時間采取隨機動作用于探索。同時,使用RMSProp作為梯度下降的辦法。

圖4 DQN偽代碼
3 實驗結果及其分析
本文將基于Deep Q-learning深度增強學習算法的海克斯棋程序與基于UCT的海克斯棋程序進行博弈。一共測試五十局,分別先手比二十五局,后手比二十五局。
經過博弈結果,可發現基于深度增強學習算法的海克斯棋程序勝率很大,證實了基于深度增強學習算法改進的有效性。在一定程度上增加了找到最優落子坐標的概率,從而大幅提升了算法效率。
4 結束語
本文將深度增強學習和海克斯棋的博弈相結合并開展相應研究。深度強化學習算法組成部分的算法與相應公式,包括Q learning算法,AlphaGo和卷積神經網絡結構等。實驗結果表明,結合了深度強化學習算法的海克斯棋可以通過不斷的訓練與博弈,提升博弈的能力。

