衛星拒止情況下低精度慣導系統航姿算法研究
蔣海濤, 辛 吉, 管春洋,申爭光
(1.海裝駐北京地區第三軍事代表室,北京 100074; 2.空裝駐北京地區第二軍事代表室,北京 100074; 3.北京自動化控制設備研究所,北京 100074)
0 引言
隨著導航技術和微加工技術的發展,微機電系統(Micro-Electro-Mechanical System,MEMS)慣性器件與衛星導航、磁航向計和氣壓高度計等組成的導航系統,廣泛應用于低成本軍用飛行器和商用飛行器。在電磁環境復雜、衛星干擾強烈的使用場景中,例如軍事要地、重要工業區域和復雜地形環境下,衛星導航輔助的低精度慣導系統往往會失效。無衛星輔助的情況下,低精度慣導系統的水平姿態隨時間發散較快,進而會造成飛行器控制系統失穩失控。
在衛星拒止的情況下,低精度慣導系統如何利用慣性器件信息和飛行器的動力學模型保持水平姿態精度是當今學者研究的重點方向。文獻[1]提出了一種低成本高精度航姿系統,通過擴展Kalman濾波進行數據融合以獲得姿態的準確輸出,姿態角動態精度優于2°。文獻[2]提出了利用運動狀態判別,根據運動狀態采用不同的量測值進行Kalman濾波以估計姿態誤差角,從而提高航向姿態精度。文獻[3]設計了由3個微陀螺儀、3個微加速度計和3個微磁航向計組成的航姿參考系統,利用加速度計對磁航向計數據進行正交化處理,并利用基于最小二乘法的橢球擬合校正方法對測量數據進行校正。文獻[4]研究了基于磁航向計的航姿測量系統誤差補償。由于磁航向計體積小、成本低,在商業級和娛樂級飛行器中使用廣泛[5]。而在軍事領域,由于任務區的電磁環境復雜,受到環境磁場以及載體的硬鐵磁場和軟鐵磁場的影響,磁航向計測量值誤差大,不能作為可靠穩定的傳感器。
針對巡飛型飛行器的飛行特點,本文基于重力矢量和載體的動力學特性,提出了一種基于動態檢測和Kalman數據融合[6-8]的航姿算法[9-10]。本算法中航向角和姿態角根據三軸陀螺儀數據進行實時更新,經過動態判斷和飛控狀態判斷,Kalman濾波器對水平加速度數據進行數據融合,并在低動態情況下進行量測更新,以修正水平姿態誤差。
1 低精度慣性導航的航姿算法研究
低精度的慣性導航系統的陀螺漂移通常大于40(°)/h,加速度計零位誤差大于2mg。由于陀螺漂移誤差大,水平姿態角采用傳統姿態角解算方法發散較快。本文采用Kalman濾波方式,利用水平加速度計測量值為觀測量,對水平姿態角誤差進行估計和修正。本方法的原理與慣導自對準計算水平姿態角的原理相同[11-13],當載體晃動即存在有害加速度(載體加速、轉彎引起的向心加速度)時,水平姿態角誤差較大,且姿態誤差與有害加速度的大小正相關。
1.1 慣性導航自主對準原理
慣導自對準的計算采用直接解析法,即通過矩陣運算直接求解出載體的姿態。在靜態情況下,采用重力矢量g、地球自轉矢量w和2個向量的叉乘V計算載體坐標系相對于導航坐標系的姿態矩陣[14]
(1)
(2)
式中,gb為載體坐標系下的加速度;wb為載體坐標系下的角速度;Vb=gb×wb。
(3)
為降低傳感器高頻噪聲及高頻環境晃動的影響,加速度和角速度需要取一段時間的均值進行計算。
對準誤差的分析參見文獻[15],在此直接給出分析結論
(4)
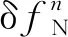
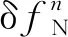
1.2 航姿模式Kalman濾波器設計
根據航姿系統的特點,Kalman濾波器的系統狀態方程采用3個失準角誤差和3個陀螺漂移誤差共六維,觀測方程采用水平加速度計的測量值,其中狀態方程定義如下

(5)
式中,F(t) 為t時刻連續狀態方程系統矩陣;w(t)為t時刻系統隨機噪聲向量。
根據Kalman濾波狀態量建立系統誤差模型,建立系統方程如下
(6)
即F(t)中非零元素如下
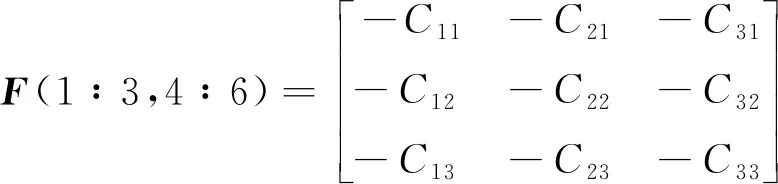
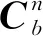
狀態變量定義如下
X=[φNφUφEεxεyεz]T
其中:X為Kalman濾波估計狀態量;φN、φU、φE、εx、εy、εz分別為北向失準角、天向失準角、東向失準角、X陀螺漂移、Y陀螺漂移和Z陀螺漂移。
當系統處于低動態時,加速度計測量值主要為重力矢量,而2個水平方向的分量幾乎為0,因此有以下關系式成立
(7)
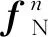
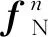
H為測量矩陣
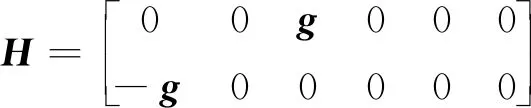
式中,g為當地重力加速度。
1.3 濾波流程
濾波過程中,每對陀螺和加速度計進行一次采樣即計算一次系統轉移矩陣,并根據濾波周期對系統矩陣進行離散化,如下所示
(8)
Φk,k-1=Fsum
式中,Tn為慣性導航周期,此處為0.005s。離散化完成后對Fsum清零。
連續系統離散化以后為離散系統,離散系統的模型方程為
(9)
1.4 航姿模式反饋修正算法
Kalman濾波器估計出水平失準角后,對水平姿態角進行誤差補償,為保證輸出水平姿態的平穩性,對修正值進行限幅,采用固定周期(1s)修正的方式。
當滿足水平失準角修正條件后,同時修正2個水平失準角,修正量限幅為φLimit°。記修正量分別為φN和φE
(10)
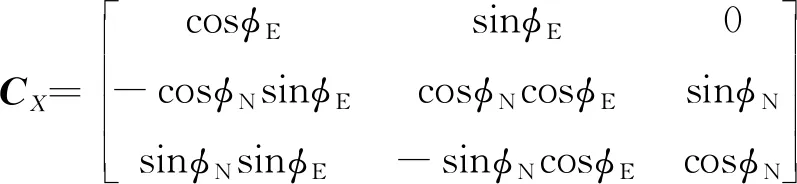
(11)
修正后,從Xk中對應元素扣掉修正值
X1=X1-φNX3=X3-φE
式中,X1和X3分別為Kalman濾波估計狀態量X的第1項(北向失準角φN)和第3項(東向失準角φE)。
2 飛行器動態檢測
飛控模塊根據目前的控制指令發送給航姿系統當前飛行器的飛行狀態。在飛控模塊發送平飛狀態時,受到結構干擾、推阻不匹配和風力等影響,飛行器可能處于側滑或小角度轉彎等飛行狀態,因此需要利用慣測信息進行低動態判斷。低動態的判斷門限跟載體的飛行狀態、轉彎特性和控制品質密切相關。根據低空固定翼飛行器的飛行特點和動力學特性,低動態需要同時滿足以下3個條件:
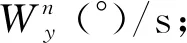
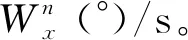
選用一組具有轉彎和直航的飛行試驗數據如圖1所示,對低動態判斷進行分析。根據動態情況判斷,在飛行器航向機動時,首先進行滾轉,通過X向角速度1s均值(見圖2)的門限2(°)/s,可以先于Y向角速度和合加速度判斷出航向機動,但是X向角速度僅在機動的前段和后段;通過Y軸角速度1s均值(見圖3)的門限0.5(°)/s,可以判斷出航向存在持續性的轉動,作為X向角速度判斷的延續;合加速度的門限(見圖4)0.2m/s2作為Y軸角速度判斷的補充,不僅可以判斷出存在航向機動時的向心加速度,還可以判斷出縱向和天向的加速狀態。3個量聯合使用可以確保載體處于低動態飛行狀態。
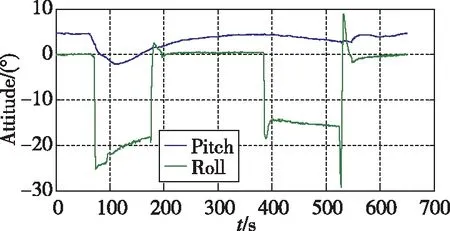
圖1 飛行器飛行姿態Fig.1 Attitude of the aircraft
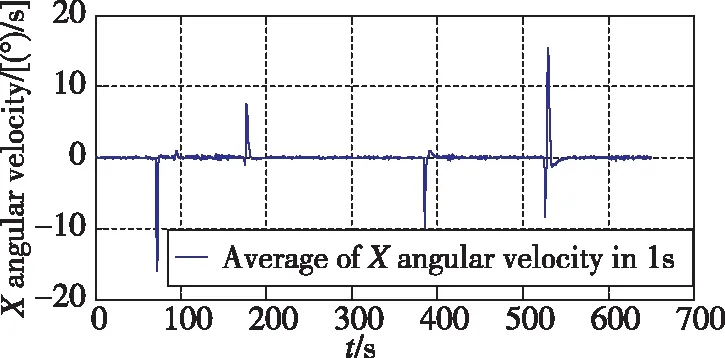
圖2 X向角速度1s均值(門限Fig.2 Average of X angular velocity in 1s(threshold
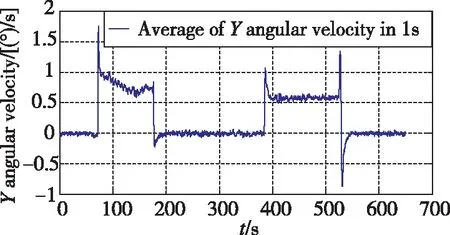
圖3 Y向角速度1s均值(門限Fig.3 Average of Y angular velocity in 1s(threshold
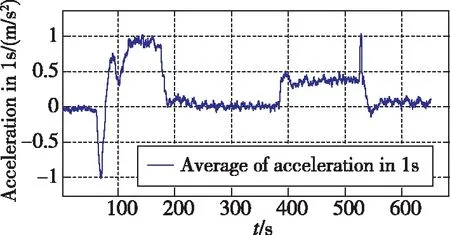
圖4 合加速度1s均值(門限Fig.4 Average of acceleration in 1s(threshold
3 仿真驗證
根據上述算法和策略,利用實際飛行數據進行離線仿真,飛行器為固定翼巡飛器,采用小型渦扇發動機,任務半徑100km。下面繪制曲線均為進入航姿模式后系統輸出的結果,誤差的比較基準為實際飛行的慣性衛星組合導航結果。三軸陀螺漂移約為40(°)/h,加速度計零位約為2mg。
濾波參數設置如下
P0=diag{(5°)2,(15°)2,(5°)2,(200°/3600s)2, (200°/3600s)2,(200°/3600s)2}
Q=diag{(40°/3600s)2,(40°/3600s)2,(40°/3600s)2, (5°/3600s)2,(5°/3600s)2,(5°/3600s)2}
R=diag{(0.1m/s2)2,(0.1m/s2)2}
飛行器的飛行軌跡為U形軌跡如圖5所示,航向角和水平姿態曲線分別如圖6和圖1所示。飛行器處于低動態情況下(根據低動態判斷結果),在直飛段可以利用航姿濾波器進行水平失準角修正。航向角由于缺乏航向傳感器(磁航向計、雙天線衛星導航接收機等)的輔助,依靠航向陀螺精度保證航向角的準確性。航向陀螺設為40(°)/h,導航600s的航向角誤差約為6.7°,能夠滿足飛行器穩定控制飛行的要求。若飛行器中存在精度較高且可靠的航向角信息,可以對航向角進行進一步修正,以保證航向角的精度。
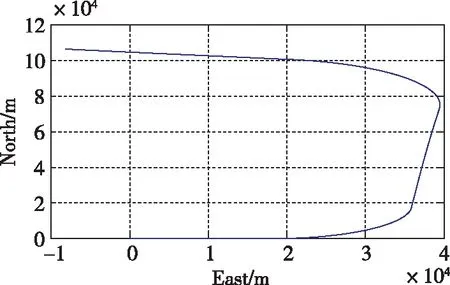
圖5 飛行軌跡Fig.5 Flight path
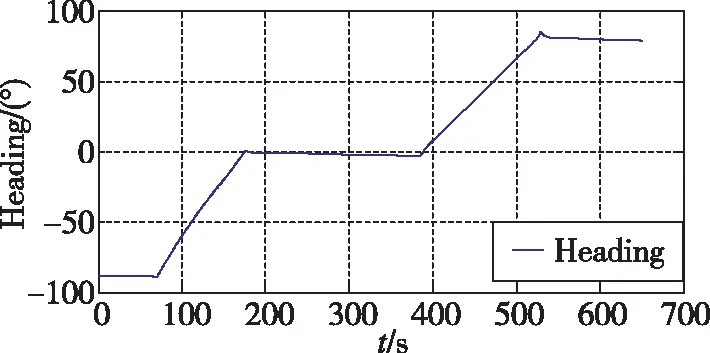
圖6 飛行器飛行航向角Fig.6 Heading angle of the aircraft
當導航模式未采用航姿算法時,水平姿態采用慣性解算的方式,隨時間發散較快如圖7所示,無法維持飛行器長時間穩態飛行。當導航模式采用航姿算法時,飛行器在直飛段的飛行動態滿足低動態判斷門限,航姿濾波器利用水平加速度計的信息進行濾波,濾波收斂后反饋校正水平姿態,水平姿態誤差快速變小至零附近,如圖8所示;飛行器進入轉彎段則不滿足低動態判斷門限,航姿濾波器不進行量測更新只進行時間更新,水平姿態誤差不進行反饋校正,水平姿態誤差發散趨勢與純慣性狀態一致,水平姿態誤差如圖8所示。航姿模式計數和修正次數計數如圖9所示,在低動態情況下,航姿模式計數每1s累加1次,非低動態情況下航姿模式計數維持不變。在航姿模式下,當姿態角每修正1次時,修正計數累加1次,非航姿模式時清零。結合圖8和圖9可以看出,在航姿模式下,隨著修正次數的累加,東向和北向失準角誤差逐漸變小,濾波器估計的水平失準角準確。
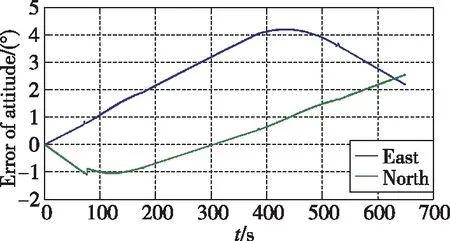
圖7 無航姿模式輔助情況下水平姿態角誤差Fig.7 Attitude error without the assist of attitude and heading reference

圖8 航姿模式輔助情況水平姿態角誤差Fig.8 Attitude error with the assist of attitude and heading reference
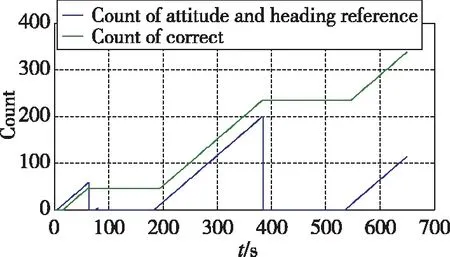
圖9 航姿模式計數累計值Fig.9 Count of attitude and heading reference
4 結論
在衛星拒止情況下,低精度慣導系統利用航姿算法可以維持水平姿態在較高的精度,滿足飛行器的飛行控制要求。
1)本文的航姿算法是一種適用于低空巡飛型固定翼無人機和旋翼型無人機等裝備的低成本慣導系統在衛星拒止情況下的航向姿態計算方法。
2)本文利用機動狀態判斷和飛控指令相結合的方式,采用六維狀態方程和二維觀測方程的Kalman濾波器估計和修正水平失準角,水平姿態誤差可控制在2°以內。

