集群空間控制框架下的四旋翼編隊飛行研究

戴邵武，趙超輪，趙國榮，劉伯彥，羅鑫輝

(海軍航空大學岸防兵學院，煙臺 264001)

0 引言

近年來，無人機行業發展迅速，在軍用和民用領域得到了廣泛應用。單架無人機由于固有的局限性，無法完成復雜的任務，人們便希望通過多無人機間的協調、合作，以產生整體大于部分之和的效果。其中，編隊控制問題是多無人機系統協同合作的基礎和難點，也是研究的熱點。根據信息交互控制策略的不同，多無人機協同控制方式主要分為集中式控制和分布式控制[1-2]。其中，集中式控制策略要求編隊中至少有1架無人機能夠獲取其他所有無人機的狀態信息，通過集中運算得到每架無人機的控制指令并發送給其他無人機，該策略控制精度高且易于實現，但編隊規模受限；分布式控制策略則僅需要獲取相鄰幾架無人機的狀態信息便可實現編隊，適用于大規模編隊，但全局性不強。在具體編隊控制方法方面，目前主流的方法有領航跟隨法[3]、虛擬結構法[4]、基于行為法、人工勢場法以及基于一致性理論的方法[5]。以上編隊控制方法各有優劣，適用于不同的任務需求，也常組合使用以達到期望的編隊控制效果[6]。本文采用的集群空間控制方法(Cluster Space Control Method)并非主流控制方法，是由美國圣塔克拉拉大學機器人系統實驗室提出的一種適用于多移動機器人編隊控制的理論[7]。該方法的突出優勢是編隊參考點的位置可任意配置，允許編隊結構全自由度變化，控制精度較高。該方法目前已成功應用于無人車[8]和飛艇[9]等多智能體編隊控制中，但將該方法應用到四旋翼上的研究文獻很少，國內則幾乎沒有關于集群空間控制的文獻。

四旋翼無人機因可垂直起降、定點懸停、機動靈活等優勢，近年來備受關注，應用前景廣闊。由于將集群空間控制方法應用到四旋翼上的研究還不深入，可供參考的文獻很少，且考慮到對于無人機編隊控制問題，通常先以實現二維平面編隊作為基礎[10]，一般選用2～4架無人機來驗證所設計控制算法的有效性[11-12]。因此，本文研究了二維平面上的四旋翼編隊控制問題，并以3架無人機為例說明算法的有效性。文獻[8]應用集群空間控制方法，設置平面編隊的參考原點位置位于3個機器人的中心，而本文將編隊參考原點位置與其中1架無人機位置重合，使編隊結構更為簡單，以減少運算量。

對于單機控制，基于四旋翼動力學模型，采用內外環結構和經典串級PID控制實現位姿控制；對于編隊控制，采用集中控制策略，在集群空間控制框架下建立編隊整體與單機的運動學關系，集群控制指令由不完全微分PD控制器產生，相較常規PD控制，其抗高頻干擾能力較強。

1 集群空間控制方法

集群空間控制是一種能夠指定、控制、監控多移動機器人編隊的理論[7]。集群空間控制的本質是將n個機器人系統視為一個實體，或稱作一個集群，并用位置量、方位量、與編隊形狀相關的量等來表示集群屬性。在設計編隊控制器前，需先定義兩組狀態變量，分別為集群變量和單機變量。前者是基于集群屬性選擇的一組適合指定、控制、監控編隊狀態的變量；后者是基于機器人單機屬性選擇的一組狀態變量。然后通過運動學轉換建立集群變量與單機變量的聯系。

1.1 集群空間變量

考慮由n個機器人組成的系統，假設每個機器人具有m個自由度，其中平移自由度為p，旋轉自由度為r，即m=p+r。則n-機器人系統中所有單機相對于慣性坐標系的位置及旋轉角度可由nm個變量來完整表示。換言之，完整描述n-機器人系統的狀態至少需要nm個變量。假設n個機體坐標系分別由obixbiybizbi，i=1,2,…,n表示，慣性坐標系由odxdydzd表示，編隊坐標系由ocxcyczc表示。

對于六自由度n-機器人系統，機體坐標系相對慣性坐標系的狀態可由(xi,yi,zi,φi,θi,ψi)表示，編隊坐標系相對慣性坐標系的狀態可由(xc,yc,zc,φc,θc,ψc)表示，其中x、y、z表示三維位置，φ、θ、ψ表示3個姿態角。通過上述分析可知，要完整表示六自由度n-機器人系統的編隊狀態，至少需要6n個變量，本文將描述編隊狀態的變量稱為集群變量，并用ci,i=1,2,…，6n表示，集群變量與(xi,yi,zi,φi,θi,ψi)和(xc,yc,zc,φc,θc,ψc)存在一定的函數關系，即

c1=f1(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

c2=f2(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

?

c6n=f6n(xc,yc,zc,φc,θc,ψc,x1,y1,z1,φ1,

θ1,ψ1,…,xn,yn,zn,φn,θn,ψn)

(1)

集群變量的選取根據不同任務需求會有差異，一般包括編隊位置、編隊方位、單機與編隊的相對方位、編隊形狀4個方面。編隊位置用于表示編隊相對慣性系的位置，在單機自由度均相同的前提下，編隊位置量的數量可用p表示；編隊方位用于表示編隊坐標系相對慣性坐標系的方位關系，編隊方位量的數量可用o表示，當n≥p=3時，則o=3，否則，o=p-1；單機與編隊的相對方位量表示每個單機相對編隊系的方位，用nr個變量便可構成；編隊形狀用于描述編隊的幾何關系，編隊形狀量的數量用s表示，假設共有nm個集群變量來描述編隊的狀態，則s=nm-p-o-nr=(n-1)p-o。一般從以上4個方面選取集群變量，便能夠清晰、直觀、全面地刻畫編隊的狀態。

1.2 集群運動學關系

因為編隊控制的指令最終要發送給每個單機去執行，所以需要建立集群變量與單機變量的運動學關系。

(1)位置運動學

定義集群變量構成的向量為C，所有單機變量構成的向量為R，并分別稱為集群位置向量和單機位置向量。兩者均為nm維列向量，兩者關系如下

(2)

(3)

稱式(2)為正向位置運動學關系式，式(3)為逆向位置運動學關系式，以此建立集群變量與單機變量的聯系。

(2)速度運動學

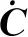
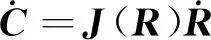
(4)

其中

(5)

式(4)實現了從單機速度向量到集群速度向量的映射。反過來，有

(6)

其中，J-1(C)為逆雅克比矩陣，為

中糧寧夏年產2萬t葡萄酒及配套種植基地項目的建設內容，符合我國釀酒行業 “糧食酒向水果酒轉變”的產業政策要求，是國家發展和改革委員 《產業結構調整指導目錄（2011年本）》中鼓勵的農產品基地建設和生態系統恢復與重建工程，同時也符合寧夏發展葡萄產業、建設優質釀酒葡萄種植基地的戰略部署。

(7)

可見，隨著單機數量和自由度的增加，集群變量會相應增加，運動學關系式會變得相對復雜，必然導致機間交互的信息量增大。故文獻[7]中提到，在現有技術程度上，若采用集中控制策略，在該控制方法下編隊機器人的數量規模大約在10個以內。

2 四旋翼編隊控制系統設計

首先建立四旋翼單機模型,然后進行編隊控制器設計。

2.1 四旋翼模型

本文采用十字形四旋翼，如圖1所示。四旋翼是一個非線性、多變量、高度耦合、欠驅動系統[13]。假設四旋翼是剛體結構，機體幾何對稱、質量對稱，且幾何中心與重心重合。

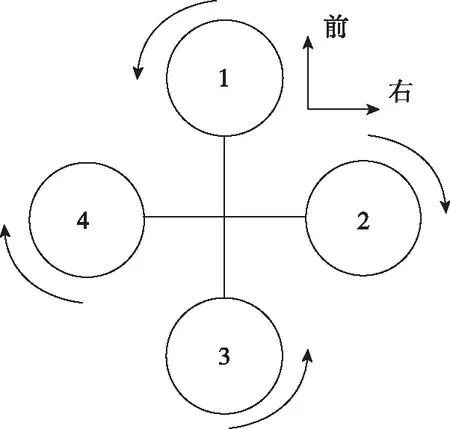
圖1 十字形四旋翼Fig.1 Cross-shaped quadrotor

首先建立兩個右手坐標系，即慣性北-東-地坐標系及機體坐標系，如圖2所示。其中，慣性坐標系odxdydzd以地面任意一點為坐標原點，odxd軸指向北，odzd軸垂直地面向下；機體坐標系obxbybzb與四旋翼機體固連，以機體重心位置為坐標原點，obxb軸指向機頭方向，obzb軸在機體對稱平面內，垂直于obxb軸向下。

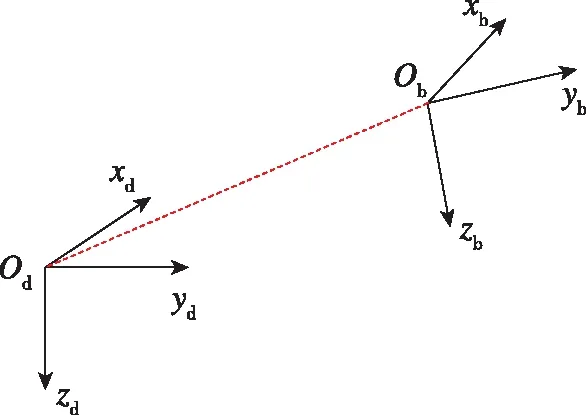
圖2 慣性坐標系與機體坐標系Fig.2 Inertial and body coordinate system

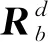
(8)

其中，cθ、sθ分別表示cosθ、sinθ，此規則同樣適用于ψ、φ。

假設四旋翼在飛行過程中，俯仰角和滾轉角都很小，總拉力約等于四旋翼的重力，則有下列近似：sinφ≈φ,cosφ≈1,sinθ≈θ,cosθ≈1,f≈m0g。在忽略陀螺效應、-ω×(J·ω)項及空氣阻力的情況下，采用牛頓-歐拉法可以得到水平通道與高度通道相互解耦的四旋翼動力學模型[14]為

(9)

四旋翼飛行器控制采用內外環結構，內環控制姿態，外環控制位置，內外環均使用經典串級PID控制[14]。

2.2 編隊控制器

本文以3架四旋翼無人機為例，設計了相應的集群控制算法，實現了二維平面內的編隊控制。圖3所示為相關的參考直角坐標系，分別為慣性坐標系odxdyd、編隊坐標系ocxcyc、機體坐標系obixbiybi，i=1,2,3。后文中將機體坐標系簡記為oixiyi。受領航跟隨法啟發，編隊坐標系是以無人機1的中心位置為坐標原點，無人機2到無人機1中心位置連接線的延長線為ocxc軸，其垂線為ocyc軸；機體坐標系以無人機機體中心為坐標原點，機頭方向為oixi軸，其垂線為oiyi軸。3架無人機的幾何關系如圖4所示。

圖3 平面3架無人機的參考坐標系Fig.3 Reference frames for three UAVs on the plan

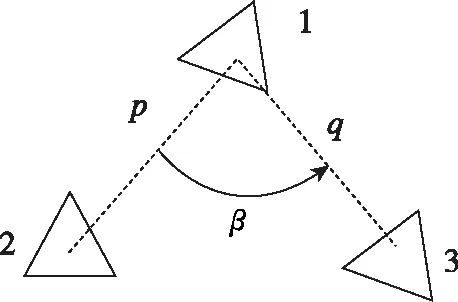
圖4 3架無人機的幾何關系Fig.4 Geometric relation of three UAVs

基于上述坐標系，為描述編隊及單機屬性，按照1.1節所述規則，首先選擇一組集群變量C和一組單機變量R

C=(xc,yc,θc,φ1,φ2,φ3,p,q,β)T

(10)

R=(x1,y1,θ1,x2,y2,θ2,x3,y3,θ3)T

(11)

其中，(xc,yc)為編隊參考點在慣性系下的二維位置，由于編隊參考點與無人機1重合，無人機1相當于編隊的領航者。(xi,yi)為無人機i在慣性系下的二維位置坐標，定義無人機i相對慣性系的偏航角θi為odxd軸到oixi軸的夾角；定義編隊基準角θc為odxd軸到ocxc軸的夾角；無人機i相對編隊坐標系的偏航角φi為ocxc軸到oixi軸的夾角;無人機1到2的距離為p，無人機1到3的距離為q;以無人機1為三角形頂點的角為β。

3架無人機的通信拓撲圖如圖5所示。無人機2和3將自身狀態信息發送給無人機1，無人機1對獲取的所有無人機的信息進行集中處理,解算得到各無人機的控制指令后，再發送給其他無人機。

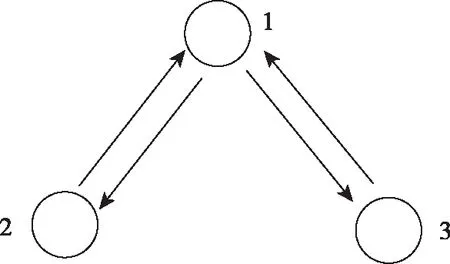
圖5 3架無人機的通信拓撲圖Fig.5 Communication topology of three UAVs

基于上述選擇的集群和單機狀態變量，下面給出了編隊系統的正向及逆向位置運動學關系式。正向位置運動學方程為C=KIN(R)，展開為式(12)

(12)

逆向位置運動學方程為R=INKIN(C)，展開為式(13)

(13)

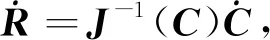
(14)

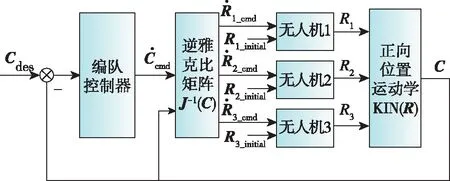
圖6 編隊控制框圖Fig.6 Formation control architecture

出于簡化的目的，同時考慮四旋翼特點，可設定在飛行過程中，無人機單機期望偏航角始終為恒定值，由單機控制器直接實現自身偏航角控制。因此，集群變量由9個簡化為6個，即C=(xc,yc,θc,p,q,β)T。相應的單機變量簡化為R=(x1,y1,x2,y2,x3,y3)T。

考慮到無人機在飛行過程中存在隨機擾動，而常規PD控制中的微分項易引進高頻干擾，使控制指令出現突跳，對控制系統不利。若在控制器中加入低通濾波器，則可明顯抑制高頻干擾。因此，編隊控制器采用不完全微分PD控制器[15]，控制器結構如圖7所示。

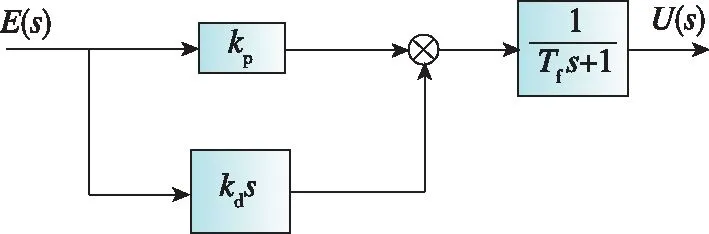
圖7 不完全微分PD控制器Fig.7 Incomplete differential PD controller

最終，集群變量誤差值通過編隊控制器和運動學轉換得到單機控制指令，進而發送給單機控制器，作為單機x、y通道的速度指令。

3 仿真分析

利用MATLAB對3架四旋翼無人機的編隊控制算法進行仿真，驗證其編隊控制的性能。編隊控制器參數如表1所示。

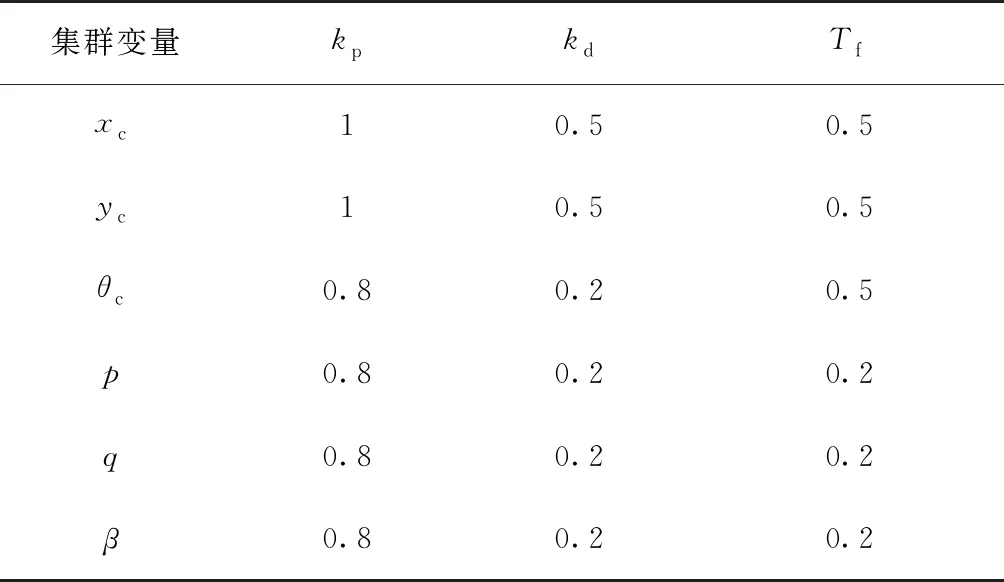
表1 不完全微分PD控制器參數

假設3架無人機均在5m高度懸停，無人機1、2、3的初始二維位置分別為(5,5)、(3,3)、(3,7)，期望的編隊狀態為

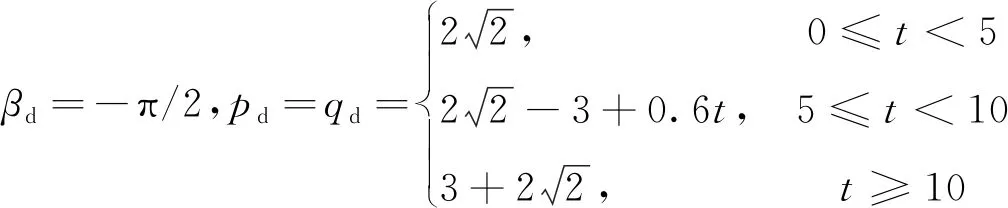
在3架無人機的實際位置輸出端分別加入幅值為0.05、0.1、0.1，采樣時間均為0.5s的隨機干擾，仿真時間30s，仿真步長0.02s。圖8(a)為編隊飛行的二維軌跡，其中在0s、9s、15s、30s時刻對無人機的位置做了標記，無人機1、2、3分別用五角星、圓形和菱形表示。可見在飛行過程中，3架無人機能夠形成穩定的三角形編隊，且相對位置唯一確定，能夠較好地實現隊形放大和隊形保持任務。

由圖8(b)可見，領航者無人機1的y方向跟蹤誤差控制在1.3m以內，x方向跟蹤誤差在1.1m以內，此位置誤差實質與單機控制器有關；在隊形放大過程中，距離量p、q的誤差在0.9m以內；在隊形保持過程中，距離量p、q的誤差小于0.12m，隊形保持效果較好。圖8(c)中，角度θc的誤差小于0.015rad，β的誤差小于0.04rad。圖8(d)中，vxc和vyc表示發送給無人機的速度指令，數字1、2、3對應無人機編號，在5s時進行隊形放大，可見速度指令進行了合理調整，在有隨機信號的干擾下，指令曲線較為平滑。

圖9所示為在常規PD編隊控制下生成的速度指令曲線，與圖8(d)對比易見，引入不完全微分能夠明顯抑制隨機擾動對系統帶來的影響。

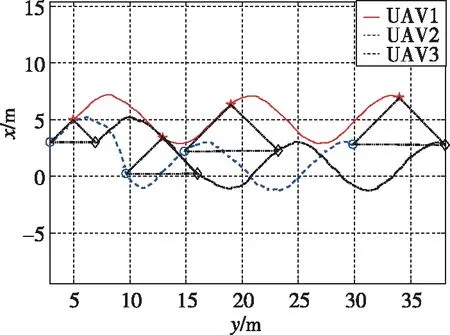
(a)編隊飛行軌跡

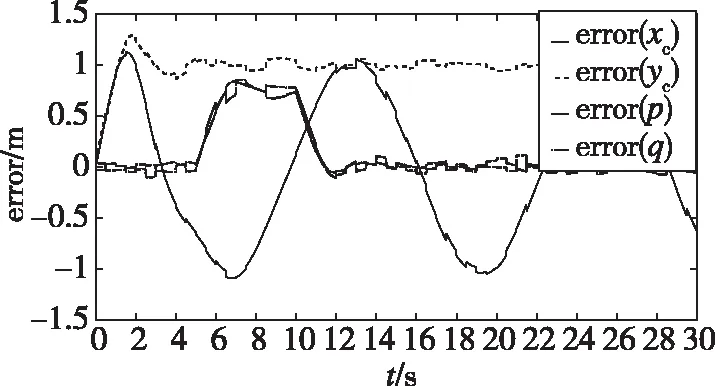
(b)位置、距離誤差曲線

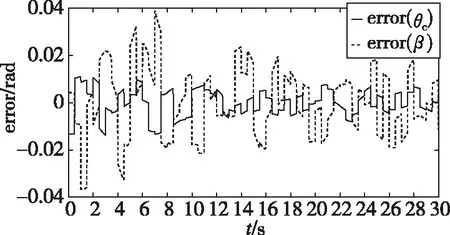
(c) 角度誤差曲線

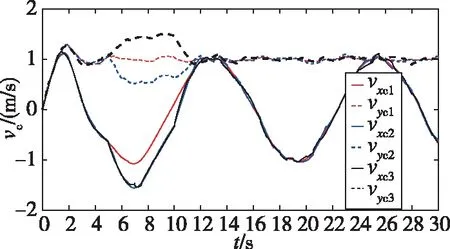
(d)3架無人機的速度指令圖8 不完全微分PD編隊控制仿真圖Fig.8 Incomplete differential PD formation control simulation diagram

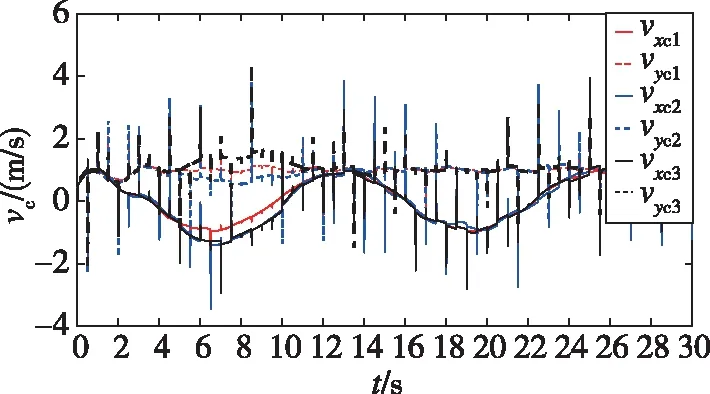
圖9 常規PD編隊控制下的速度指令Fig.9 Velocity commands of conventional PD formation control

4 結束語

本文主要介紹了集群空間控制方法的概念，然后將該方法應用到四旋翼編隊控制中，并以3架四旋翼為例，驗證了所設計編隊控制算法的有效性。在考慮存在隨機擾動的情況下，設計了不完全微分PD控制器以產生集群控制指令，實現了編隊放大與隊形保持任務。結果表明，該控制算法能夠實現多架四旋翼無人機的編隊控制，清晰完整地描述指定編隊狀態，隊形保持的精度較高，與常規PD控制相比，具有較強的抗高頻干擾能力。