面向結構化場景的激光雷達點云高精度配準與定位方法

2021-02-03 02:47:48何洪磊賴際舟向林浩李志敏

導航定位與授時 2021年1期

何洪磊，賴際舟，呂品，向林浩，李志敏

(1.南京航空航天大學，南京 211106； 2.中國船級社，北京 100007)

0 引言

近年來，隨著科技的進步，機器人行業得以快速發展，無人設備在巡檢、運輸等領域扮演著重要角色。同時為了完成愈加復雜的工作任務，人們對其定位導航能力也提出了更高的行業要求。在該過程中，激光雷達憑借測距精度高、感知能力強等特點逐漸成為衛星拒止環境下無人設備的主要導航傳感器之一。

針對機器人的室內導航問題，當前工程上主流的導航方案為：首先通過多源信息融合算法構建高精度激光點云地圖[1-3]，隨后將無人設備實時激光雷達數據與構建的先驗地圖進行匹配，從而獲得機體位姿。該過程首先需將雷達系與地圖系對齊，實現機體位姿初始化，因此需要通過點云粗配準[4-5]的方法進行機體的初始定位。點云配準分為特征提取與位姿解算兩部分，Dong Z.等提出了在算法前端采用基于局部特征描述[6-9]的點云特征提取方法建立點云關聯，如三維形狀上下文、點特征直方圖、快速點特征直方圖等，該類方法通常適用于特征豐富的小場景，但在大型的結構化場景下該類特征區分度較低，導致特征關聯的錯誤率較高。Zhang X.等提出了基于概率統計的多元正態分布變換(Normal Distributions Transform, NDT)[10]，建立了兩幀點云之間的關聯，然而受限于特征配準的收斂性，該方法不適用于位姿差異過大的兩幀點云。上述兩種方法均采用基于迭代的位姿解算方法，計算量較大，并且在大型結構化場景的點云配準過程中易陷入局部最優[11]，從而產生錯誤的導航解算。

因此在結構化環境中，需要一種魯棒的特征提取方法，S.Ochmann和S.Oesau等提出了空間結構的平面模型化表示方法[12-13]，可以從三維點云中恢復建筑物的空間環境結構。在大型結構化場景中，該類特征具有一定魯棒性，然而該類算法復雜度較高，同時利用該類特征進行無人系統初始定位的方法還未見文獻報道。

基于此，本文提出了一種基于多平面空間模型的激光雷達點云配準方法。首先對傳統空間結構恢復方法進行改進，采用優化特征直方圖[14]實現了空間平面的快速分割與擬合，以及大型結構化空間環境的模型化表示。隨后為了避免解算過程中的局部最優問題，不同于傳統算法中基于迭代的位姿求解方法，本文算法采用空間平面線性匹配方式實現兩幀點云面特征的快速配準，提高了計算效率。

1 基于多平面模型的面特征快速提取方法

三維激光雷達點云數據量龐大，所以需要通過特征提取的方式建立兩幀點云之間的關聯。傳統方法對特征的數量要求大，增加了算法的整體計算負擔，且在特征稀疏或特征區分度較小的環境中，難以保證算法的特征精度。針對該問題，本文利用結構化環境特點，采用優化的特征直方圖思想實現了空間點云的快速分割聚類，并根據平面一致性對點集進行合并，最終實現了高效、魯棒空間面特征的提取。

1.1 基于特征直方圖的三維點云快速分割方法

首先，根據李新春等[15]提出的方法對濾波后激光雷達點云的法線nk進行計算

(1)

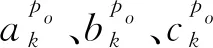
不同于傳統的特征提取算法(如FPFH)，本文算法采用平面作為點云特征，考慮到法向量相同的點可以近似為同一個平面點，采用優化的特征直方圖對法線特征進行快速分析，以實現點云的粗聚類。將點云法線的三維特征區間asec、bsec、csec分別等分為m個特征區間，并排列組合形成m×m×m個三維特征區間，最終構建出法線特征直方圖(見圖1)。

圖1 基于特征直方圖的特征區間劃分方法Fig.1 Feature interval partitioning method based on feature histograms

第i個特征chari表示的特征區間為

(2)

(3)

將點云根據其法向量特征的數值投放到不同的特征區間，形成激光雷達三維掃描特征直方圖，從而實現三維點云的快速粗分割。

1.2 基于平面一致性的點集合并及平面擬合方法

在式(3)中，當閾值m選取較大時，chari的特征空間較小，同一平面點云易被分割成多個部分。因此，點云快速粗分割后，需根據平面一致性將同一平面但不同特征區間的點云進行合并。

選取數據量最大的λ組特征區間內的點云進行粗擬合，歸一化后可得平面方程

(4)

其中，t為chari內點云數據量；d為方程歸一化常數。

(5)

(6)

則根據式(5)計算兩法線向量pi和pj之間的偏差eij。當eij≤δ時，將兩特征區間內的點云數據合并。根據設定的空間模型平面數量，保留點云數據量最大的k組點云。最后采用隨機抽樣一致性(Random Sample Consensus, RANSAC)算法去除各組點云離群點以提高平面魯棒性，并將濾波后的平面點云擬合生成k個平面，形成平面方程的形式如式(7)

(7)

2 基于多平面模型的特征快速配準方法

假設機體為剛體，所有的運動變換均為剛體變換，則可利用兩幀點云之間的特征關聯建立位姿優化函數，從而求取位姿變換最優解。傳統算法采用基于迭代的目標函數優化方法，然而該方法計算量較大，并且當特征精度較差或環境特征區分度較低時，迭代算法易陷入局部最優。因此，本文基于線性最小二乘對面特征進行配準。首先通過空間平面排序建立兩幀點云的面特征關聯，而后通過線性最小二乘實現平面的快速配準，使得算法在提高計算效率的同時避免陷入局部最優。

2.1 基于排序的特征關聯方法

當雷達點云與地圖點云分別擬合出k個平面后，需要建立兩幀點云平面間的特征關聯。然而若兩幀點云平面是無序的，隨機關聯平面特征，則其后續計算的時間復雜度為O((k-1)!n)；若兩幀點云平面是有序的，則其后續計算的時間復雜度為O((k-1)n)。因此，為了提高計算效率，對點云平面進行排序。

首先求取點云平面與XOY平面交線

(8)

(9)

式中

(10)

如圖2所示，若空間平面模型與XOY平面相交為6條直線，根據式(9)和式(10)計算可得

gl6>gl4>gl1>gl3>gl5>gl2

(11)

將平面按照位置分數從大到小的順序排序，即可實現平面的逆時針有序排列。

圖2 空間平面快速排序方法Fig.2 Spatial plane quicksort method

2.2 基于線性最小二乘的配準快速解算方法

通過兩幀點云的面特征關聯，可形成k-1組有效平面約束。定義第i組對應平面的平面系數為(ai,1,bi,1,ci,1)與(ai,2,bi,2,ci,2)。選取待求解變量tx、ty、θ，其平面系數的轉換關系如式(12)

[-ai,1-bi,1ci,2-ci,1]T=

(12)

其中，tx、ty、θ分別表示兩幀點云之間的水平位置差及航向角偏差。傳統基于迭代的目標函數解算方法計算量較大且易陷入局部最優。為了避免該問題，本文采用線性求解的思路進行解算

ai,2ci,1tx+bi,2ci,1ty=ci,2-ci,1

(13)

若空間平面中所有平面均垂直于地面，則式(13)為恒等式。因此，構建待優化函數如式(14)

(14)

式中

(15)

采用最小二乘擬合算法進行解算，可得

Aξ=B

(16)

式中

(17)

(18)

(19)

式(17)中

(20)

2.3 平面配準的最優解選定方法

兩幀點云的點云平面均逆時針排列后，一共可產生k-1種面特征關聯情形。首先通過預置區域Φ對位姿解算結果進行粗篩選，并定義誤差函數ek對其配準度作進一步分析，從而提取最優解

(21)

(22)

式中

(23)

(24)

將配準結果經過式(21)和式 (22)解算后，保留誤差最小解即為兩幀點云配準的最優解。

3 實驗驗證及分析

本文分別通過Gazebo仿真與室內結構化場景模擬實驗對算法進行驗證與分析。采樣一致性初始配準(Sample Consensus Initial Alignment, SAC-IA)與迭代最近點(Iterative Closest Point, ICP)算法是當前主流的點云配準算法，因此，將本文算法與SAC-IA算法及SAC+ICP組合算法的點云配準結果進行對比分析。

3.1 Gazebo仿真驗證與分析

仿真平臺采用Gazebo機器人仿真系統，Gazebo是一款三維動力學仿真軟件，軟件內置物理引擎，能夠對環境、無人系統、傳感器進行高保真的物理模擬。船艙的近觀檢驗[16]是保障船舶安全航行的重要手段，采用無人機取代人工進行船艙檢驗具有重大的經濟效益。因此，在Gazebo中根據船艙真實環境構建如圖3所示仿真模型，以驗證算法的有效性，同時在仿真環境中加入障礙物以驗證算法的可靠性。

圖3 仿真環境模型Fig.3 Simulation environment

Gazebo構建無人系統包括：

1) hector quad rotor微小型飛行器載體，機體實時發布位姿真值，以對本文算法進行性能評估；

2)機載16線三維激光雷達，水平角分辨率0.3°、垂直角分辨率2°，水平視場360°、垂直視場±15°，測距誤差±2cm，測距范圍0～100m；

數據處理計算機采用Linux(Ubuntu 16.04)的機器人操作系統(Robot Operating System, ROS)，處理器為G2020，主頻2.9GHz。

仿真數據采集點如圖4所指示。其中，P0表示地圖構建原點，Pi表示激光雷達數據采集點，各點箭頭表示雷達在該點處x軸指向,黑色方塊表示障礙物位置及其姿態。

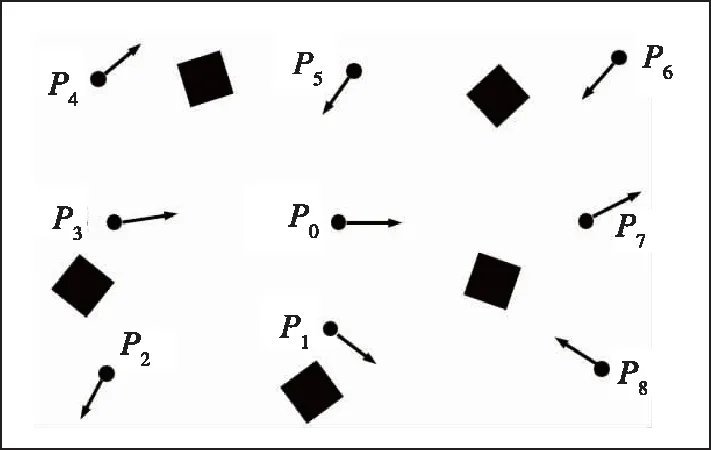
圖4 仿真數據采集點示意圖Fig.4 Simulation data acquisition point

(1)地圖點云預處理

首先對地圖點云(如圖5(a)所示)進行處理。在位姿初始化過程中，僅有鄰近地面的點云參與解算，所以根據高度值對地圖點云進行截取(如圖5(b)所示)。仿真環境相對結構化，噪點較少，故設定特征區間數量m為7，保留平面數量k為5，通過本文算法對地圖點云進行平面分割(如圖5(c)所示)。由圖可見，本文算法對地圖點云進行了較為精準的快速分割，并自動濾除障礙物點。

(a)地圖點云

(b)截取后地圖點云

(c)地圖點云分割圖5 地圖點云預處理Fig.5 Map point cloud preprocessing

以激光雷達地圖點云為目標點云，Pi各點采集到的激光雷達點云為輸入點云，進行點云配準實驗。

(2)配準精度對比分析

輸入點云與目標點云如表1所示，其中，綠色點云為目標點云，紅色點云為輸入點云。

從表1中可以看出，即使有障礙物，本文算法對三維空間點云仍然可以進行較為精準的分割，實現了空間結構的模型化處理。

點云配準后解算位姿與各點位姿參考值如表2所示。

從位置1、2、3、4點云的配準情況以及定位結果分析可以看出，SAC-IA算法的定位精度為米級，航向角平均偏差在2°以上，存在較大誤差；而本文算法定位偏差均小于0.1m，航向角偏差小于0.5°，與SAC +ICP組合算法的全局最優解具有相當的精度等級。同時這也表明了本文算法中通過大數據點云聚類擬合的面特征具有較高的精度與可靠性。

表1 點云配準對比Tab.1 Point cloud registration comparison

表2 位置1～4點云配準精度對比Tab.2 Comparison of cloud registration accuracy at position 1～4

傳統算法在解算位置5、6、7、8處位姿的過程中，產生了錯誤解算(如表3所示)。這表明傳統算法在特征區分度較小的大場景空間環境中容易產生局部最優問題。而在該情況下，本文算法依舊保持了較高的定位精度。

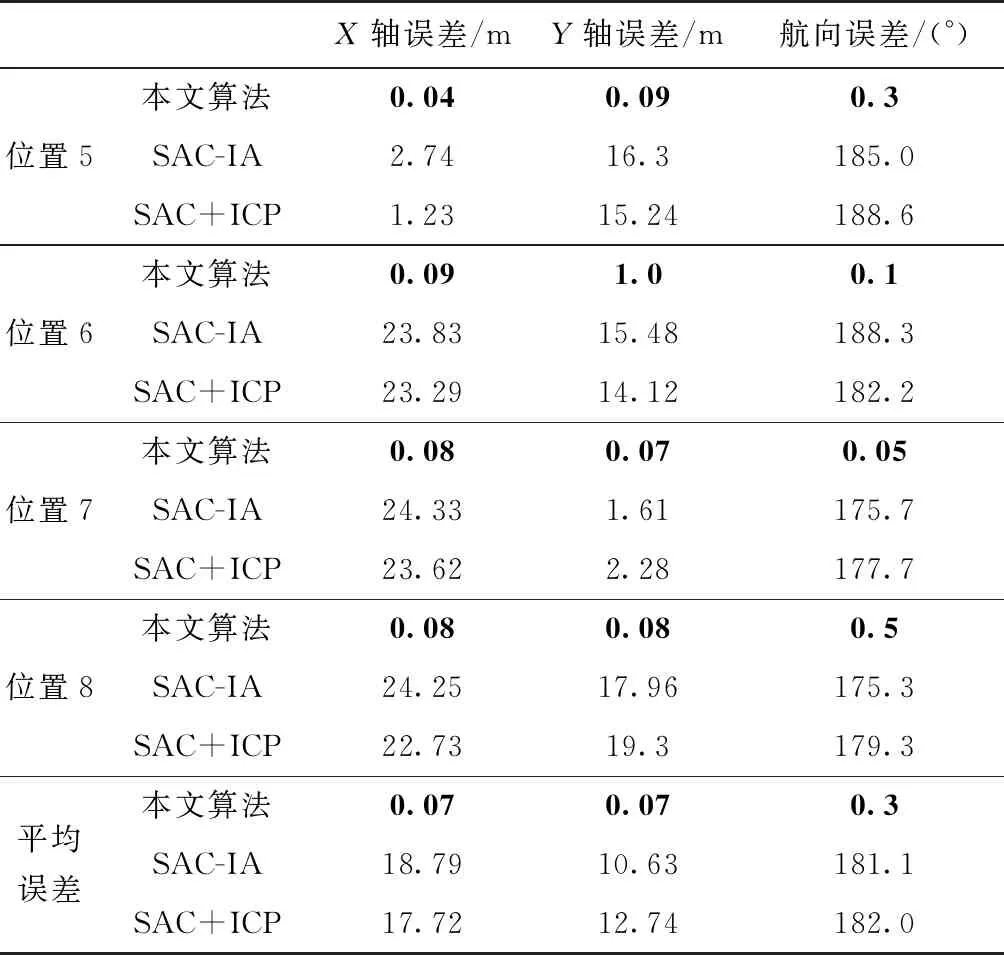
表3 位置5～8點云配準精度對比

(3)計算效率對比分析

本文算法與SAC-IA算法計算時間統計如表4所示。

表4 計算效率對比Tab.4 Computational efficiency comparison

由表4可得，本文算法的平均用時為3.1s，SAC-IA算法的平均用時為10.8s，SAC+ICP算法的平均用時為15.1s。所以在仿真實驗中，本文算法的計算效率約是SAC-IA算法的3.5倍，是SAC +ICP算法的5倍。相較于傳統算法，本文算法減少了特征提取的數量，在位姿求解過程中，本文算法使用線性最小二乘算法取代了傳統算法位姿解算中采用的非線性最小二乘算法，無需迭代求取最優解，從而提高了計算效率。