基于桿臂補償的多MIMU六方位倍速率標定方法

陶 冶，張東良，李建利

(1.海軍研究院，北京 100161； 2.北京航空航天大學, 儀器科學與光電工程學院, 北京 100083)

0 引言

基于微機電系統(Micro-Electro-Mechanical System，MEMS)技術的微慣性測量單元(Micro Inertial Measurement Unit，MIMU)具有成本低、體積小、易于集成等優點[1-3]，在智能手機、智能控制、行人導航及姿態測量等領域都在快速推廣應用[4-6]。如何從系統層面提高MIMU精度是學術界的研究熱點[7-9]。

通過對MIMU進行誤差建模、標定與補償是提高慣導系統輸出精度的一項關鍵技術[10]。由于小體積的MIMU的市場需求量大，需要進行批量生產和標定，且MIMU的工作機理及加工工藝等不同于傳統光學慣性器件，誤差具有強非線性和模型參數不穩定的特點[11]，傳統的標定方法難以直接用于MIMU標定。現有IMU標定方法中，通常將加速度通道與角速度通道分立標定，通過位置法標定加速度通道，角速率法標定角速度通道，標定方法復雜，數據量大[12-13]。文獻[14]提出了一種六位置+24點的機械編排方案，由于其試驗編排較簡單，且無需北向基準，而被廣泛應用；文獻[15]提出了一種六方位正反速率標定方案，取得了和文獻[14]中相同的補償效果，通過限定IMU測量中心在轉臺旋轉軸上，避免了角速率運動對加速度通道輸出的影響，僅用一組速率數據同時解算加速度和角速度通道誤差系數，標定工作量較六方位+24點法減少了3/5。但在MIMU標定應用中，需要單次實驗標定多個MIMU，MIMU節點與轉臺旋轉中心將存在桿臂。應用傳統的六方位正反速率標定方法會受到桿臂效應引起的離心加速度影響，導致標定精度下降。

本文提出了一種基于桿臂補償的多MIMU六方位倍速率標定方法。首先針對多MIMU標定過程中桿臂效應帶來標定誤差的影響機理進行了分析。然后設計了一種六方位倍速率標定方法，并建立了桿臂效應誤差補償模型和應用加權最小二乘法的誤差解算模型。最后通過試驗驗證了該方法的有效性。

1 桿臂效應影響機理分析

加速度通道誤差模型[8]

(1)

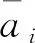
角速度通道誤差模型[8]

(2)

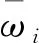
由于系統誤差嚴重影響MIMU測量精度，使用前必須進行標定。MIMU標定是指在已知輸入條件下進行多組測試，從而構成輸入輸出關系的方程組，以解算出模型中的誤差系數。

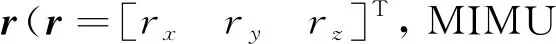
aω=ω×r×ω

(3)

則加速度通道的實際輸入ain為

ain=g+aω

(4)

將式(1)中的加速度輸入分解為已知加速度(重力加速度)和未知加速度(離心加速度)

(5)

由于在傳統六方位正反速率法的解算模型中，加速度通道輸入為重力加速度g，用傳統方法標定多MIMU會帶來離心加速度引起的標定誤差。用其解算的誤差系數進行補償的結果為

(6)

式中：ai為i軸實際加速度值；aei為i軸由于標定時的離心加速度引起的補償誤差，aei與標定時i軸離心加速度大小成正比。

2 多MIMU六方位倍速率標定方法

依據誤差模型和桿臂效應的影響分析，設計了一種基于桿臂補償的多MIMU六方位倍速率標定方法。標定設備僅需單軸速率轉臺和六面體工裝，通過12組基準數據實現了單次標定多個MIMU。

將多個MIMU安裝在六面體工裝上，分6次翻轉六面體工裝，分別使MIMU的X、Y、Z軸與轉臺ZT軸和-ZT軸(地理系天、地)重合。每個方位分別勻速轉動ω1和ω2(ω2=nω1，n≠±1)并記錄MIMU輸出。如圖1所示，每個轉速點保證旋轉360°以上。轉臺旋轉時，地球自轉角速度水平分量被調制為正弦/余弦周期信號。根據三角函數的特點，當采樣總時長為旋轉周期的整數倍時，數據求平均將剔除地球自轉角速度的影響。即將整周數據平均作為MIMU輸出，從而消除地球自轉角速度水平分量在角速度通道的輸入。

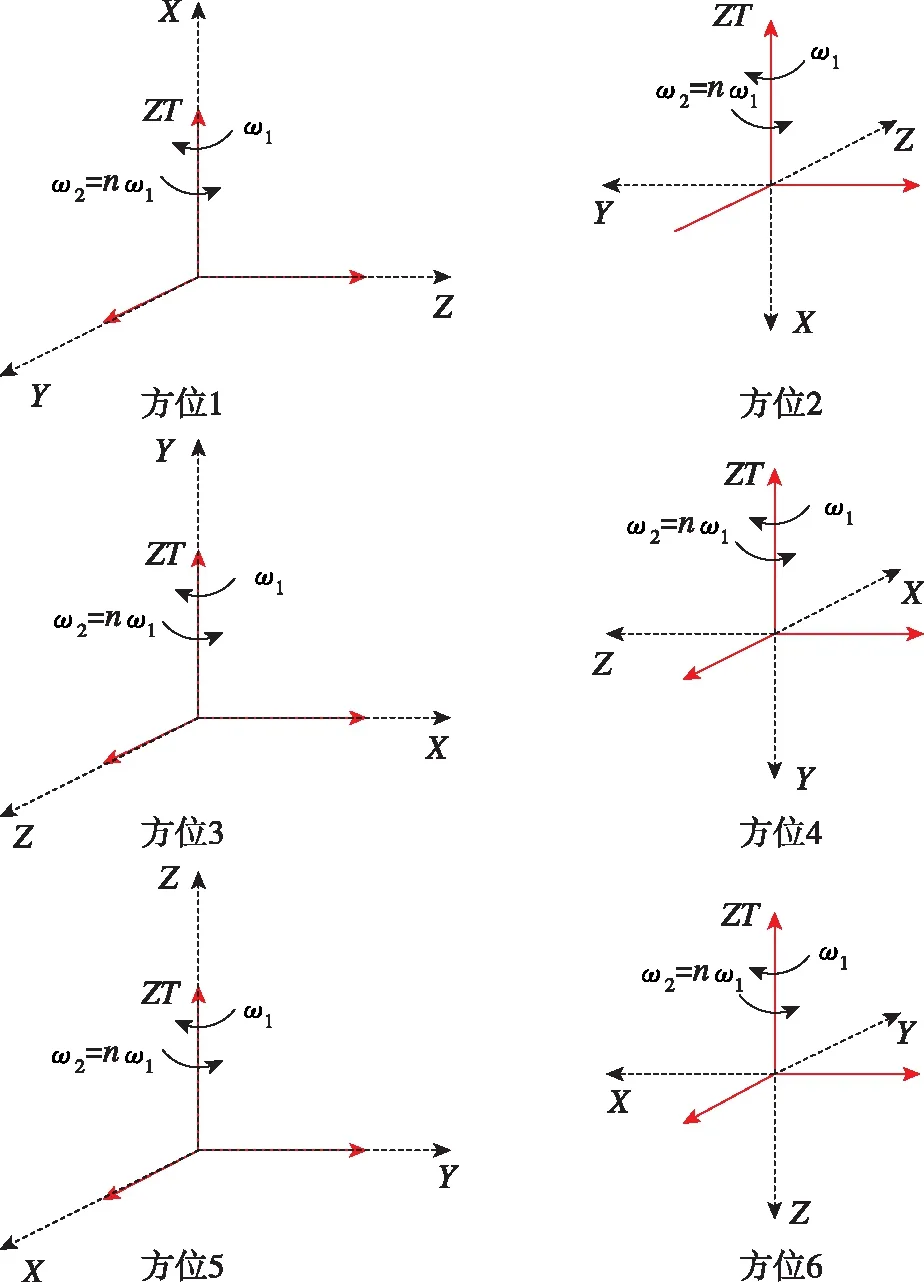
圖1 六方位倍速率標定方案Fig.1 Six-position multiplied rates calibration scheme

2.1 加速度通道誤差系數解算模型

2.1.1 建立加速度通道輸入輸出方程

根據實驗數據和式(1)，得到12組數據加速度通道輸出與輸入關系為

(7)

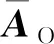
將式(7)中比力輸入AI分解為重力加速度項AI1和離心加速度項AI2，可得(分解的AI2由于含全為0的行而進行降維)

(8)

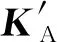
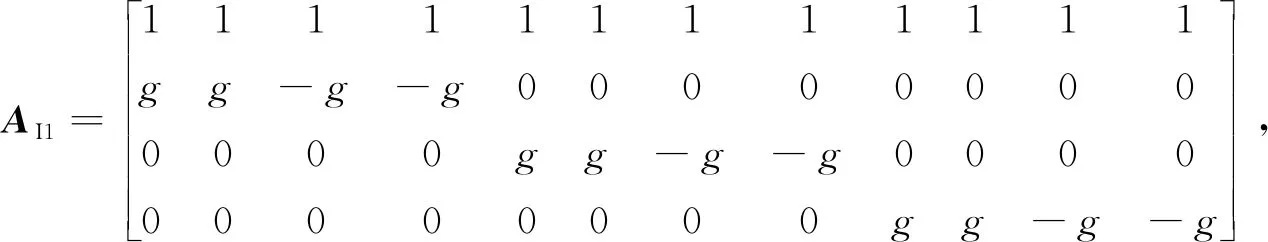
其中，ajim表示m方位ωj引起的離心加速度i軸分量。

2.1.2 離心加速度解耦

每次翻轉MIMU，ω1和ω2這2個速率點采集的數據，r是一定的，取ω2=nω1，則其離心加速度的關系為

a2im=n2a1im

(9)

根據式(9)中離心加速度大小關系可對式(8)中加速度輸入輸出方程進行解耦，從而消除離心加速度

(10)

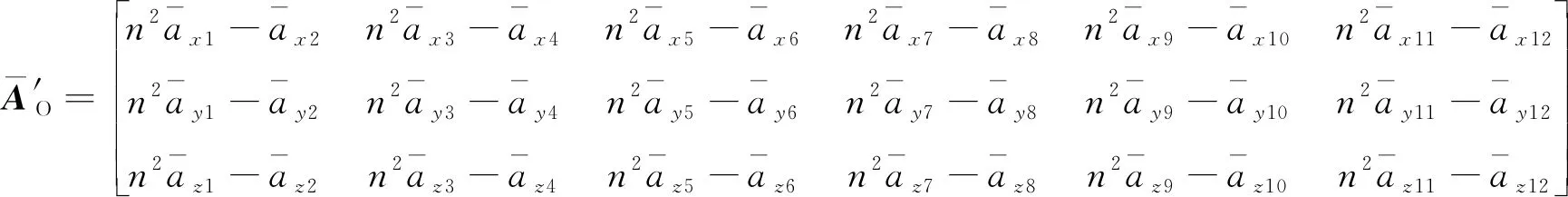
2.1.3 加速度通道誤差系數解算

消元后得到無離心加速度的輸入輸出方程(10)，應用加權最小二乘法，加速度通道12項誤差系數可由18個不相關方程組解出。在實際應用中，Z軸向上為MIMU最常用工作狀態。增大Z軸向上方位數據的權值，有助于抑制MIMU常用工作狀態的非線性和非對稱性誤差，從而提高導航系統性能。

首先在式(10)左右兩邊同時乘以六方位數據的權值矩陣σa，得到方程組

(11)

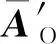
再由最小二乘法解算得到加速度通道誤差系數矩陣KA

(12)

2.2 角速度通道誤差系數解算模型

2.2.1 加速度輸入解算

由式(4)可知，角速度通道誤差系數包括比力相關項。需要先求解未知離心加速度。

對式(8)中重力加速度相關項進行消元，得到

(13)

式中

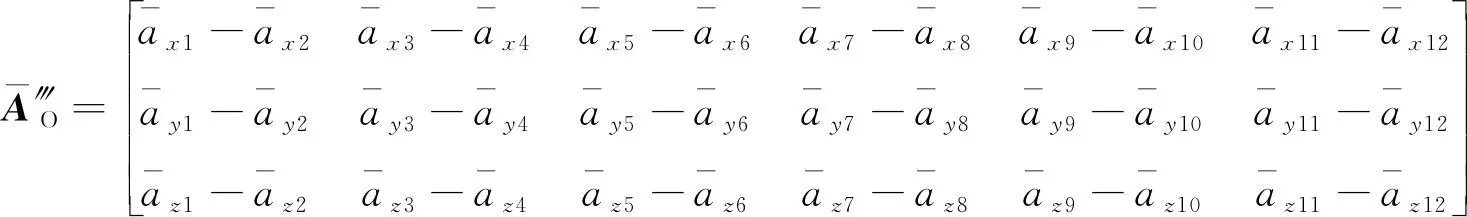
由式(13)可解出離心加速度為

(14)

2.2.2 建立角速度通道輸入輸出方程

由于地球自轉角速度水平分量經轉臺旋轉調制為正弦信號，整周期均值為0。根據式(2)中的角速度通道誤差模型，標定方法中12組數據角速度通道輸出與輸入關系為

(15)

2.2.3 加速度通道誤差系數解算

式(16)中21項角速度通道誤差系數可由36個不相關方程組解出。

首先在式(15)左右兩邊同時乘以六方位數據的權值矩陣σg，得到方程組

(16)

再由最小二乘法解算得到角速度通道誤差系數矩陣KG

(17)

3 試驗驗證

根據六方位倍速率實驗方案對2個MIMU進行標定，如圖2所示。ω1和ω2分別為10(°)/s和-30(°)/s。

圖2 多MIMU標定實驗Fig.2 Multi-MIMU calibration test

分別用傳統方法(六方位正反速率法[15])和本文方法(基于桿臂補償的六方位倍速率法：先進行桿臂補償，后進行加權最小二乘法解算)對1# MIMU和2# MIMU進行模型解算。1#MIMU誤差標定系數如表1和表2所示，2#MIMU誤差標定系數如表3和表4所示。

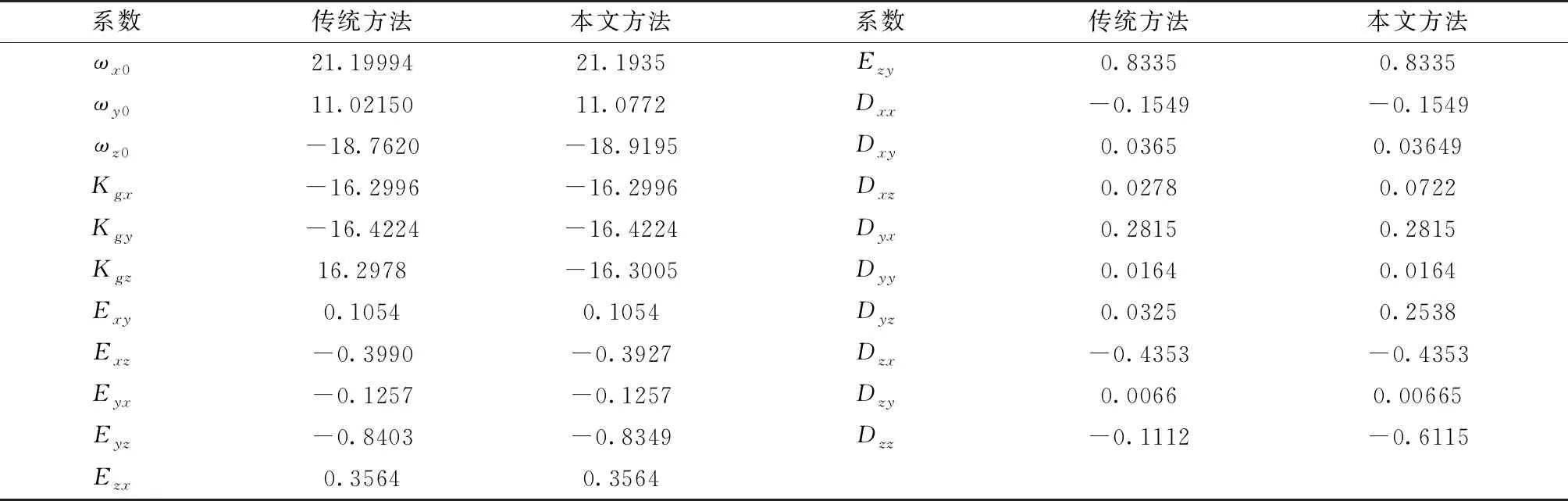
表2 1#MIMU角速度通道誤差系數

表3 2#MIMU加速度通道誤差系數

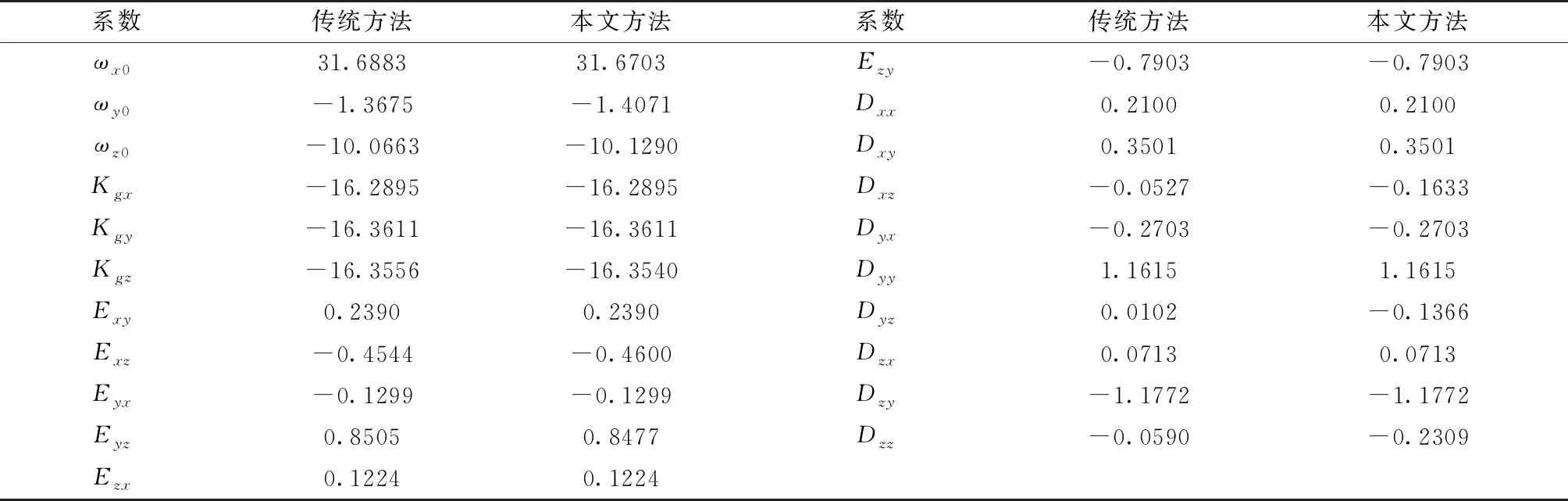
表4 2#MIMU角速度通道誤差系數

傳統方法采用正反速率標定模式，不能解決桿臂問題，導致無法準確標定Dzz參數。而本文提出的方法針對桿臂問題進行了優化，能夠相對準確地標定Dzz參數。在本文設置的標定安裝試驗條件下，MIMU的Z軸桿臂較大，標定效果較明顯。

通過對MIMU在不同運動狀態的測試數據進行補償，對加速度通道的標定結果進行驗證。分別在Z軸向上靜止、繞Z軸20(°)/s和30(°)/s旋轉狀態下進行測試，對各加速度計這一時間段內的測量誤差求取均值，統計結果如表5所示。

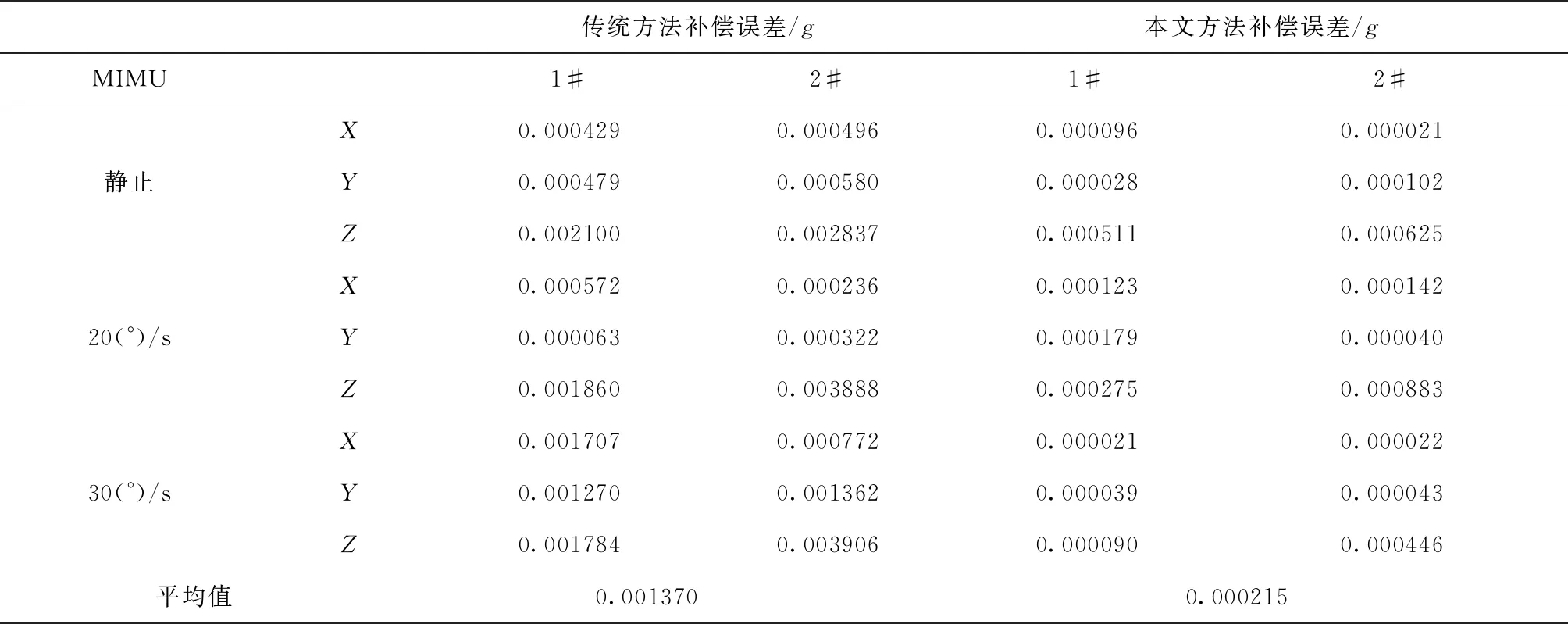
表5 加速度計誤差補償結果

綜合對比傳統方法和本文方法補償結果，常用工作方位下，本文方法相對傳統方法，單軸加速度計的補償誤差降低了84.3%。

由于實驗中單軸速率轉臺沒有北向基準，無法獲得地球自轉角速度在MIMU坐標系中的各分量值來驗證單軸陀螺儀的補償精度。使MIMU在水平面內做勻角速率運動，將X、Y軸陀螺儀測量的地球自轉角速度水平分量調制成正弦信號，通過整周平均進行消除。統計結果如表6所示。

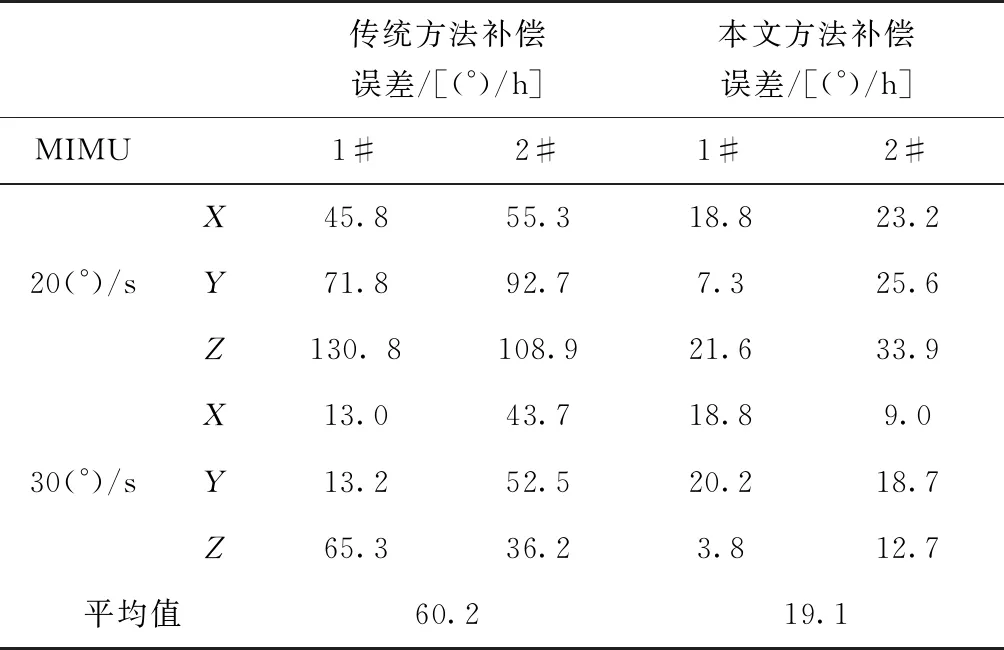
表6 陀螺儀誤差補償結果

對比傳統方法和本文方法補償結果，常用工作方位下，本文方法可以有效提高陀螺儀系統誤差補償精度，單軸陀螺儀的補償誤差降低了68.3%。

4 結論

本文分析了桿臂效應對加速度計輸出的影響機理，提出了一種六方位倍速率MIMU標定方法，并通過方程解耦對桿臂效應進行補償，應用加權最小二乘法有效抑制了非線性和非對稱性誤差。試驗結果表明，本文提出的標定方法簡易、高效。MIMU在常用工作方位下，加速度通道和角速度通道系統誤差的補償精度均有較大提高。