高速公路滿堂支架現澆箱梁施工技術分析
■張志強
(永升建設集團有限公司, 克拉瑪依 834000)
近年來,隨著我國交通體系的不斷發展,“交通強國”依然是國家發展的重要戰略方向,其中高速公路橋梁建設也在如火如荼地進行之中。 橋梁施工過程中的施工工藝對于保證橋梁后期能夠安全運營至關重要,由于滿堂支架施工方法能有效節約建設成本,眾多工程師對其進行了詳細研究,主要有:劉景雷[1]、傅菁俊[2]認為現澆箱梁具有整體性好、抗扭性能大、橫向抗彎剛度大、穩定性好等特點,采用滿堂支架是現澆箱梁施工的一種常用方法,之后結合具體的高速公路橋梁施工實例,簡要探討滿堂支架現澆箱梁的施工技術;楊安倫[3]、林元勝[4]以某高速公路滿堂支架現澆箱梁的施工作為案例進行分析,對滿堂支架現澆施工技術進行總結,可為今后解決滿堂支架現澆施工中的重、難點問題提供很好的借鑒;周興志[5]、何俊[6]針對滿堂支架現澆箱梁施工技術,結合江口至都格高速公路開陽至息烽段第二合同段實例對該技術的施工工藝進行了深入地分析,并得出滿堂支架現澆箱梁施工技術可簡化施工操作,具有較高綜合效益特點的結論;程學會[7]通過對滿堂支架現澆箱梁施工技術工程各道工序的理解對技術指標、地基處理、滿堂支架的搭設與預壓、鋼絞線安裝、箱梁砼澆筑、預應力張拉、落模等一系列技術進行闡述,并結合工程實際對澆箱梁施工技術進行了總結與淺析;張立新[8]認為現澆箱梁是高速公路橋梁的重要組成部分, 具有抗扭性能大、穩定性好、橫向抗彎剛度大的特點,可被廣泛地應用于高速公路橋梁施工當中,并從高速公路的地基處理和滿堂支架的搭設出發,深入研究了高速公路滿堂支架現澆箱梁施工技術的關鍵要點。 本文以某高速公路滿堂支架現澆箱梁施工為例,采用有限元分析軟件Midas/civil 建立了全橋模型, 重點從各施工階段箱梁的位移、縱橋向應力和彎矩,以及預拱度計算等方面對高速公路滿堂支架現澆箱梁施工技術進行了詳細分析,研究結果可為類似工程施工提供參考和借鑒。
1 工程概況
某高速公路現澆連續箱梁采用C40 混凝土進行施工,其上部結構共分為3 聯,其中一聯是4 孔26 m預應力混凝土連續梁,一聯是3 孔28 m 的預應力混凝土連續梁,最后一聯是4 孔28 m 預應力混凝土連續梁。橋梁全長為1260 m,橋面寬度為24 m,包括左右側的防護欄各0.5 m, 左右側的車道各10.0 m,以及中間的分離帶3.0 m。 由于第1 聯和第3 聯尺寸一致,故本文主要選取第1 聯和第2 聯進行分析。
2 數值建模
圖1 為采用大型有限元軟件Midas/civil 建模得到的第1 聯和第2 聯的箱梁模型圖。 方向選取時以箱梁截面橫向方向為x 軸,以箱梁截面高度方向為y 軸,以向上為z 軸。 規定以x 軸向右、y 軸向內及z軸向上為正方向。第1 聯跨徑為,模型中共有62 個節點,共61 個單元。第2 聯跨徑為,模型中共有48個節點,共47 個單元。
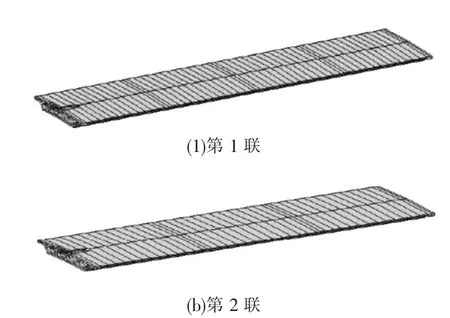
圖1 數值模型圖
橋身全部采用標號為C40 的混凝土, 其參數指標如表1 所示。在施工過程中,將施工過程分為2 個階段:(1)階段一:該階段對第1 跨和第2 跨及其懸臂端進行混凝土澆筑和張拉預應力;(2)階段二:該階段對第3 跨及第4 跨進行混凝土澆筑和張拉預應力。

表1 模型材料參數
3 數值結果分析
3.1 箱梁第1 聯數值分析
首先對箱梁的第1 聯進行分析,施工階段一時的箱梁整體位移圖如圖2 所示,由圖可知,第1 跨和第2 跨的最大撓度值分別為4.8 mm 和4.6 mm,最大撓度發生在跨中位置,沿縱橋向方向從跨中到兩邊撓度逐漸減小,直至到達兩支座處撓度趨于0。

圖2 階段一箱梁整體位移
圖3 為施工階段一時的箱梁縱橋向內力圖,包括有彎矩和應力云圖,由圖3(a)可知,彎矩最大值為32.0 kN·m,發生在第1 跨跨中位置,兩跨之間支座處彎矩方向與跨中相反,其值為19.3 kN·m。 圖3(b)為箱梁的組合應力圖,由圖可知,在第1 跨的跨中應力最大,最大值為4.1 MPa。
施工階段二時的箱梁整體位移圖如圖4 所示,由圖可知,第四跨的撓度最大,其次是第1 跨,最小的是第3 跨。 最大撓度值為5.1 mm,最大撓度發生在跨中位置,沿縱橋向方向從跨中到支座撓度逐漸減小,直至到達兩支座處撓度趨于0。
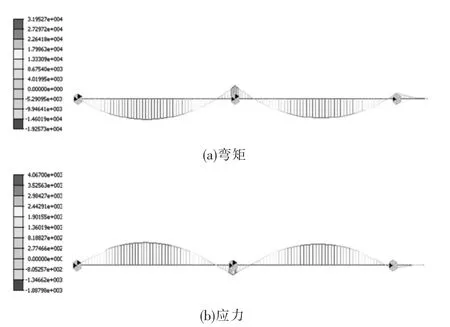
圖3 階段一箱梁縱橋向內力圖

圖4 階段二箱梁整體位移
施工階段二時的箱梁縱橋向內力圖如圖5 所示,由圖5(a)可知,彎矩最大值為33.8 kN·m,發生在第四跨跨中位置, 其次是第1 跨跨中彎矩較大。圖5(b)為箱梁的組合應力圖,由圖可知,在第4 跨的跨中應力最大,最大值為4.3 MPa。
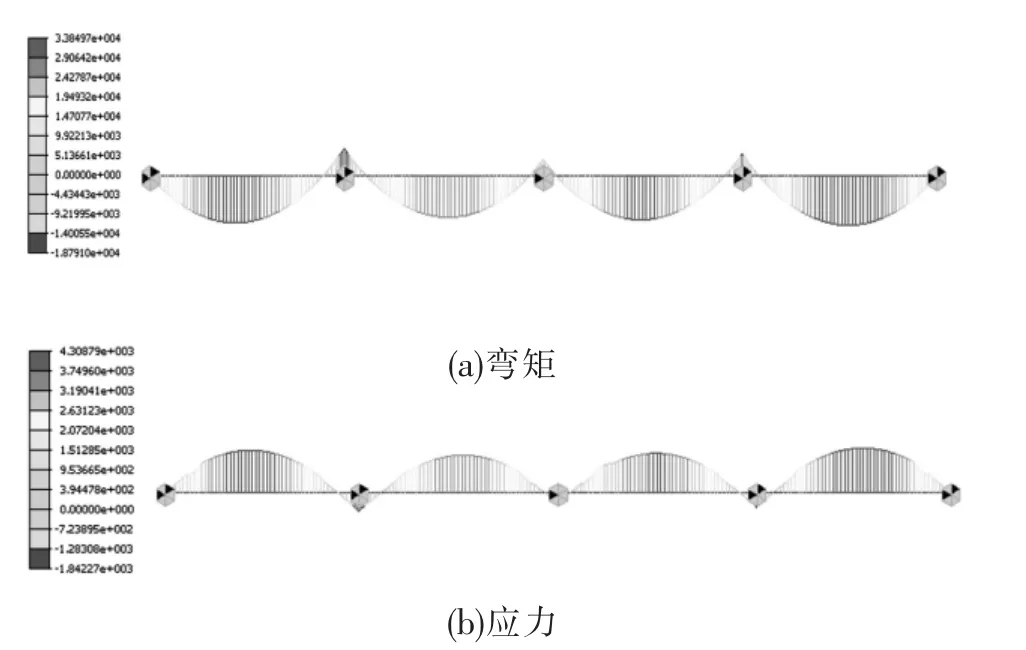
圖5 階段二箱梁縱橋向內力圖
3.2 箱梁第2 聯數值分析
對箱梁的第2 聯進行分析,圖6 為施工階段一時的箱梁整體位移圖,由圖可知,第1 跨和第2 跨的最大撓度值分別為6.1 mm 和6.0 mm, 最大撓度發生在跨中位置,沿縱橋向方向從跨中到兩邊撓度逐漸減小,直至到達兩支座處撓度趨于0。

圖6 階段一箱梁整體位移
施工階段一時的箱梁縱橋向內力圖如圖7 所示,包括有彎矩和應力云圖,由圖7(a)可知,彎矩最大值為35.9 kN·m,發生在第1 跨跨中位置,兩跨之間支座處彎矩方向與跨中相反,值為23.6 kN·m。圖7(b)為箱梁的組合應力圖,由圖可知,在第1 跨的跨中應力最大,最大值為4.6 MPa。

圖7 階段一箱梁縱橋向內力圖
施工階段二時的箱梁整體位移圖如圖8 所示,由圖可知,第3 跨的撓度最大,其次是第1 跨,最小的是第2 跨。 最大撓度值為8.8 mm,最大撓度發生在跨中位置,沿縱橋向方向從跨中到支座撓度逐漸減小,直至到達兩支座處撓度趨于0。

圖8 階段二箱梁整體位移
圖9 為施工階段一時的箱梁縱橋向內力圖,包括有彎矩和應力云圖,由圖9(a)可知,彎矩最大值為42.6 kN·m,發生在第3 跨跨中位置。 圖9(b)為箱梁的組合應力圖,由圖可知,在第3 跨的跨中應力最大,最大值為5.3 MPa。
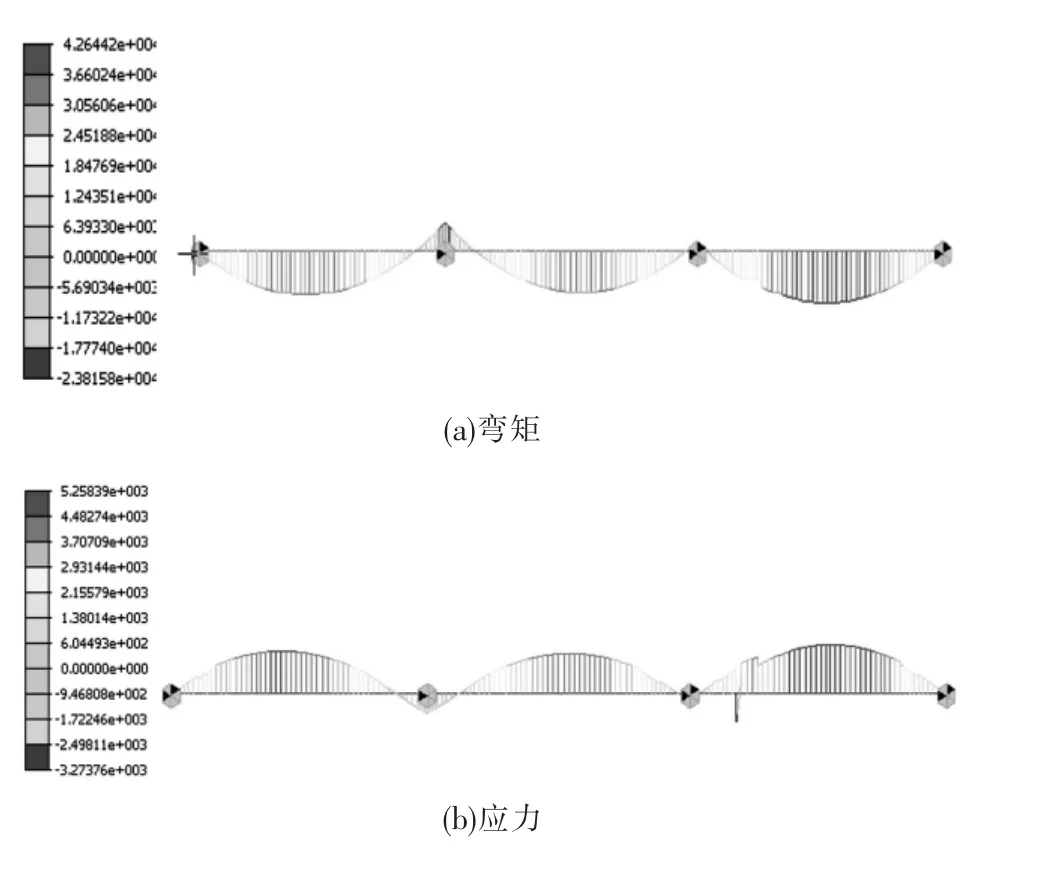
圖9 階段二箱梁縱橋向內力圖
3.3 預拱度計算方法與結果
所謂預拱度,即為抵消橋梁箱梁在荷載下產生的撓度,需要在施工時預留與位移方向相反的校正量。 預拱度的計算可采用下式進行計算:
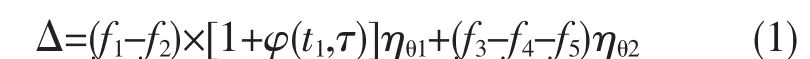
其中:f1為預應力下的位移量;f1為自重下的位移量;f3為由于體系轉換得到的附加變形;f4為橋梁二期鋪裝下的變形量;f5為在人群荷載和活荷載下的撓度;φ(t1,τ)為徐變系數;ηθ1為橋梁箱梁在前期變形時的增長系數;ηθ2為體系轉換的撓度變化增長系數。
通過計算, 得到了箱梁各孔位的預拱度計算值,如圖10 所示,計算結果可以為設計提供指導。
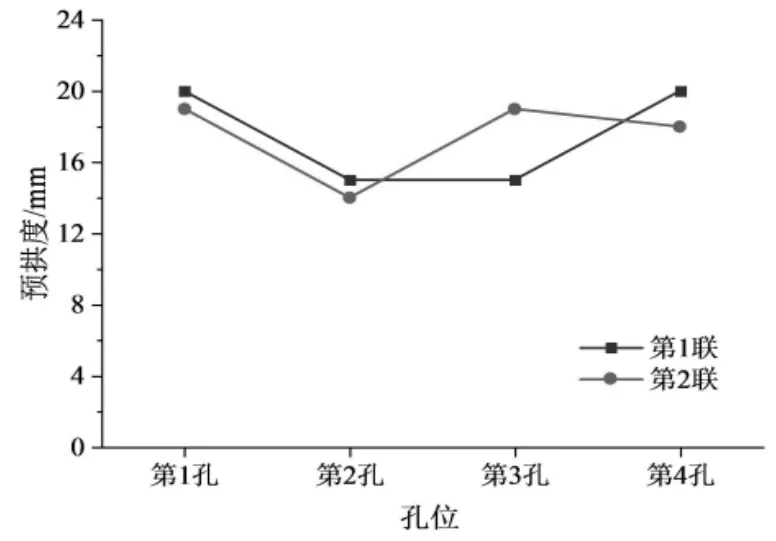
圖10 不同孔位處預拱度值
4 結論
本文以某高速公路滿堂支架現澆箱梁施工為例, 采用有限元分析軟件Midas/civil 建立了全橋模型,重點從各施工階段箱梁的位移、縱橋向應力和彎矩, 以及預拱度計算等方面對高速公路滿堂支架現澆箱梁施工技術進行了詳細分析,得到以下結論:
(1)箱梁的最大撓度均發生在跨中位置,且沿縱橋向方向從跨中到兩邊撓度逐漸減小,直至到達兩支座處撓度趨于0。
(2)對于第1 聯,施工階段一時其撓度、彎矩和應力均在的第1 跨跨中處最大;施工階段二時其撓度、彎矩和應力均在的第3 跨跨中處最大,其次是第1 跨,最小的是第3 跨。
(3)對于第2 聯,施工階段一時其撓度、彎矩和應力均在的第1 跨跨中處最大;施工階段二時其撓度、彎矩和應力均在的第3 跨跨中處最大,其次是第1 跨,最小的是第2 跨。
(4)給出了預拱度的計算方法,并通過計算得到了箱梁各孔位的預拱度計算值, 計算結果可以為設計提供指導。

